| TGraphQQ() |
| TGraphQQ(const TGraphQQ&) |
| TGraphQQ(Int_t n, Double_t* x) |
| TGraphQQ(Int_t n, Double_t* x, TF1* f) |
| TGraphQQ(Int_t nx, Double_t* x, Int_t ny, Double_t* y) |
| virtual | ~TGraphQQ() |
| void | TObject::AbstractMethod(const char* method) const |
| virtual void | TObject::AppendPad(Option_t* option = "") |
| virtual void | TGraph::Apply(TF1* f) |
| virtual void | TGraph::Browse(TBrowser* b) |
| virtual Double_t | TGraph::Chisquare(const TF1* f1) const |
| static TClass* | Class() |
| virtual const char* | TObject::ClassName() const |
| virtual void | TNamed::Clear(Option_t* option = "") |
| virtual TObject* | TNamed::Clone(const char* newname = "") const |
| virtual Int_t | TNamed::Compare(const TObject* obj) const |
| static Bool_t | TGraph::CompareArg(const TGraph* gr, Int_t left, Int_t right) |
| static Bool_t | TGraph::CompareRadius(const TGraph* gr, Int_t left, Int_t right) |
| static Bool_t | TGraph::CompareX(const TGraph* gr, Int_t left, Int_t right) |
| static Bool_t | TGraph::CompareY(const TGraph* gr, Int_t left, Int_t right) |
| virtual void | TGraph::ComputeRange(Double_t& xmin, Double_t& ymin, Double_t& xmax, Double_t& ymax) const |
| virtual void | TNamed::Copy(TObject& named) const |
| virtual void | TObject::Delete(Option_t* option = "")MENU |
| Int_t | TAttLine::DistancetoLine(Int_t px, Int_t py, Double_t xp1, Double_t yp1, Double_t xp2, Double_t yp2) |
| virtual Int_t | TGraph::DistancetoPrimitive(Int_t px, Int_t py) |
| virtual void | TGraph::Draw(Option_t* chopt = "") |
| virtual void | TObject::DrawClass() constMENU |
| virtual TObject* | TObject::DrawClone(Option_t* option = "") constMENU |
| virtual void | TGraph::DrawGraph(Int_t n, const Int_t* x, const Int_t* y, Option_t* option = "") |
| virtual void | TGraph::DrawGraph(Int_t n, const Float_t* x, const Float_t* y, Option_t* option = "") |
| virtual void | TGraph::DrawGraph(Int_t n, const Double_t* x = 0, const Double_t* y = 0, Option_t* option = "") |
| virtual void | TGraph::DrawPanel()MENU |
| virtual void | TObject::Dump() constMENU |
| virtual void | TObject::Error(const char* method, const char* msgfmt) const |
| virtual Double_t | TGraph::Eval(Double_t x, TSpline* spline = 0, Option_t* option = "") const |
| virtual void | TObject::Execute(const char* method, const char* params, Int_t* error = 0) |
| virtual void | TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0) |
| virtual void | TGraph::ExecuteEvent(Int_t event, Int_t px, Int_t py) |
| virtual void | TGraph::Expand(Int_t newsize) |
| virtual void | TGraph::Expand(Int_t newsize, Int_t step) |
| virtual void | TObject::Fatal(const char* method, const char* msgfmt) const |
| virtual void | TNamed::FillBuffer(char*& buffer) |
| virtual TObject* | TGraph::FindObject(const char* name) const |
| virtual TObject* | TGraph::FindObject(const TObject* obj) const |
| virtual Int_t | TGraph::Fit(const char* formula, Option_t* option = "", Option_t* goption = "", Axis_t xmin = 0, Axis_t xmax = 0)MENU |
| virtual Int_t | TGraph::Fit(TF1* f1, Option_t* option = "", Option_t* goption = "", Axis_t xmin = 0, Axis_t xmax = 0)MENU |
| virtual void | TGraph::FitPanel()MENU |
| virtual Double_t | TGraph::GetCorrelationFactor() const |
| virtual Double_t | TGraph::GetCovariance() const |
| virtual Option_t* | TObject::GetDrawOption() const |
| static Long_t | TObject::GetDtorOnly() |
| Bool_t | TGraph::GetEditable() const |
| virtual Double_t | TGraph::GetErrorX(Int_t bin) const |
| virtual Double_t | TGraph::GetErrorXhigh(Int_t bin) const |
| virtual Double_t | TGraph::GetErrorXlow(Int_t bin) const |
| virtual Double_t | TGraph::GetErrorY(Int_t bin) const |
| virtual Double_t | TGraph::GetErrorYhigh(Int_t bin) const |
| virtual Double_t | TGraph::GetErrorYlow(Int_t bin) const |
| virtual Double_t* | TGraph::GetEX() const |
| virtual Double_t* | TGraph::GetEXhigh() const |
| virtual Double_t* | TGraph::GetEXhighd() const |
| virtual Double_t* | TGraph::GetEXlow() const |
| virtual Double_t* | TGraph::GetEXlowd() const |
| virtual Double_t* | TGraph::GetEY() const |
| virtual Double_t* | TGraph::GetEYhigh() const |
| virtual Double_t* | TGraph::GetEYhighd() const |
| virtual Double_t* | TGraph::GetEYlow() const |
| virtual Double_t* | TGraph::GetEYlowd() const |
| virtual Color_t | TAttFill::GetFillColor() const |
| virtual Style_t | TAttFill::GetFillStyle() const |
| TF1* | TGraph::GetFunction(const char* name) const |
| TH1F* | TGraph::GetHistogram() const |
| virtual const char* | TObject::GetIconName() const |
| virtual Color_t | TAttLine::GetLineColor() const |
| virtual Style_t | TAttLine::GetLineStyle() const |
| virtual Width_t | TAttLine::GetLineWidth() const |
| TList* | TGraph::GetListOfFunctions() const |
| virtual Color_t | TAttMarker::GetMarkerColor() const |
| virtual Size_t | TAttMarker::GetMarkerSize() const |
| virtual Style_t | TAttMarker::GetMarkerStyle() const |
| Double_t | TGraph::GetMaximum() const |
| Int_t | TGraph::GetMaxSize() const |
| virtual Double_t | TGraph::GetMean(Int_t axis = 1) const |
| Double_t | TGraph::GetMinimum() const |
| Int_t | TGraph::GetN() const |
| virtual const char* | TNamed::GetName() const |
| virtual char* | TObject::GetObjectInfo(Int_t px, Int_t py) const |
| static Bool_t | TObject::GetObjectStat() |
| virtual Option_t* | TObject::GetOption() const |
| virtual void | TGraph::GetPoint(Int_t i, Double_t& x, Double_t& y) const |
| virtual Double_t | TGraph::GetRMS(Int_t axis = 1) const |
| virtual const char* | TNamed::GetTitle() const |
| virtual UInt_t | TObject::GetUniqueID() const |
| Double_t* | TGraph::GetX() const |
| TAxis* | TGraph::GetXaxis() const |
| Double_t* | TGraph::GetY() const |
| TAxis* | TGraph::GetYaxis() const |
| virtual Bool_t | TObject::HandleTimer(TTimer* timer) |
| virtual ULong_t | TNamed::Hash() const |
| virtual void | TObject::Info(const char* method, const char* msgfmt) const |
| virtual Bool_t | TObject::InheritsFrom(const char* classname) const |
| virtual Bool_t | TObject::InheritsFrom(const TClass* cl) const |
| virtual void | TGraph::InitExpo(Double_t xmin = 0, Double_t xmax = 0) |
| virtual void | TGraph::InitGaus(Double_t xmin = 0, Double_t xmax = 0) |
| virtual void | TGraph::InitPolynom(Double_t xmin = 0, Double_t xmax = 0) |
| virtual Int_t | TGraph::InsertPoint()MENU |
| virtual void | TObject::Inspect() constMENU |
| void | TObject::InvertBit(UInt_t f) |
| virtual TClass* | IsA() const |
| virtual Bool_t | TGraph::IsEditable() const |
| virtual Bool_t | TObject::IsEqual(const TObject* obj) const |
| virtual Bool_t | TObject::IsFolder() const |
| Bool_t | TObject::IsOnHeap() const |
| virtual Bool_t | TNamed::IsSortable() const |
| virtual Bool_t | TAttFill::IsTransparent() const |
| Bool_t | TObject::IsZombie() const |
| virtual void | TGraph::LeastSquareFit(Int_t m, Double_t* a, Double_t xmin = 0, Double_t xmax = 0) |
| virtual void | TGraph::LeastSquareLinearFit(Int_t n, Double_t& a0, Double_t& a1, Int_t& ifail, Double_t xmin = 0, Double_t xmax = 0) |
| virtual void | TNamed::ls(Option_t* option = "") const |
| void | TObject::MayNotUse(const char* method) const |
| virtual Int_t | TGraph::Merge(TCollection* list) |
| virtual void | TAttLine::Modify() |
| virtual Bool_t | TObject::Notify() |
| static void | TObject::operator delete(void* ptr) |
| static void | TObject::operator delete(void* ptr, void* vp) |
| static void | TObject::operator delete[](void* ptr) |
| static void | TObject::operator delete[](void* ptr, void* vp) |
| void* | TObject::operator new(size_t sz) |
| void* | TObject::operator new(size_t sz, void* vp) |
| void* | TObject::operator new[](size_t sz) |
| void* | TObject::operator new[](size_t sz, void* vp) |
| TGraphQQ& | operator=(const TGraphQQ&) |
| virtual void | Paint(Option_t* opt = "") |
| void | TGraph::PaintGraph(Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt) |
| void | TGraph::PaintGrapHist(Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt) |
| virtual void | TGraph::PaintStats(TF1* fit) |
| virtual void | TObject::Pop() |
| virtual void | TGraph::Print(Option_t* chopt = "") const |
| virtual Int_t | TObject::Read(const char* name) |
| virtual void | TGraph::RecursiveRemove(TObject* obj) |
| virtual Int_t | TGraph::RemovePoint()MENU |
| virtual Int_t | TGraph::RemovePoint(Int_t ipoint) |
| virtual void | TAttFill::ResetAttFill(Option_t* option = "") |
| virtual void | TAttLine::ResetAttLine(Option_t* option = "") |
| virtual void | TAttMarker::ResetAttMarker(Option_t* toption = "") |
| void | TObject::ResetBit(UInt_t f) |
| virtual void | TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU |
| virtual void | TAttFill::SaveFillAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1001) |
| virtual void | TAttLine::SaveLineAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1, Int_t widdef = 1) |
| virtual void | TAttMarker::SaveMarkerAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1, Int_t sizdef = 1) |
| virtual void | TGraph::SavePrimitive(ostream& out, Option_t* option = "") |
| virtual void | TGraph::Set(Int_t n) |
| void | TObject::SetBit(UInt_t f) |
| void | TObject::SetBit(UInt_t f, Bool_t set) |
| virtual void | TObject::SetDrawOption(Option_t* option = "")MENU |
| static void | TObject::SetDtorOnly(void* obj) |
| virtual void | TGraph::SetEditable(Bool_t editable = kTRUE)TOGGLE GETTER |
| virtual void | TAttFill::SetFillAttributes()MENU |
| virtual void | TAttFill::SetFillColor(Color_t fcolor) |
| virtual void | TAttFill::SetFillStyle(Style_t fstyle) |
| void | SetFunction(TF1* f) |
| virtual void | TGraph::SetHistogram(TH1* h) |
| virtual void | TAttLine::SetLineAttributes()MENU |
| virtual void | TAttLine::SetLineColor(Color_t lcolor) |
| virtual void | TAttLine::SetLineStyle(Style_t lstyle) |
| virtual void | TAttLine::SetLineWidth(Width_t lwidth) |
| virtual void | TAttMarker::SetMarkerAttributes()MENU |
| virtual void | TAttMarker::SetMarkerColor(Color_t tcolor = 1) |
| virtual void | TAttMarker::SetMarkerSize(Size_t msize = 1) |
| virtual void | TAttMarker::SetMarkerStyle(Style_t mstyle = 1) |
| virtual void | TGraph::SetMaximum(Double_t maximum = -1111)MENU |
| virtual void | TGraph::SetMinimum(Double_t minimum = -1111)MENU |
| virtual void | TNamed::SetName(const char* name)MENU |
| virtual void | TNamed::SetNameTitle(const char* name, const char* title) |
| static void | TObject::SetObjectStat(Bool_t stat) |
| virtual void | TGraph::SetPoint(Int_t i, Double_t x, Double_t y) |
| virtual void | TGraph::SetTitle(const char* title = "")MENU |
| virtual void | TObject::SetUniqueID(UInt_t uid) |
| virtual void | ShowMembers(TMemberInspector& insp, char* parent) |
| virtual Int_t | TNamed::Sizeof() const |
| virtual void | TGraph::Sort(Bool_t (*)(const TGraph*, Int_t, Int_t) greater = &TGraph::CompareX, Bool_t ascending = kTRUE, Int_t low = 0, Int_t high = -1111) |
| virtual void | Streamer(TBuffer& b) |
| void | StreamerNVirtual(TBuffer& b) |
| virtual void | TObject::SysError(const char* method, const char* msgfmt) const |
| Bool_t | TObject::TestBit(UInt_t f) const |
| Int_t | TObject::TestBits(UInt_t f) const |
| virtual void | TGraph::UseCurrentStyle() |
| virtual void | TObject::Warning(const char* method, const char* msgfmt) const |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const |
| void | TGraph::Zero(Int_t& k, Double_t AZ, Double_t BZ, Double_t E2, Double_t& X, Double_t& Y, Int_t maxiterations) |
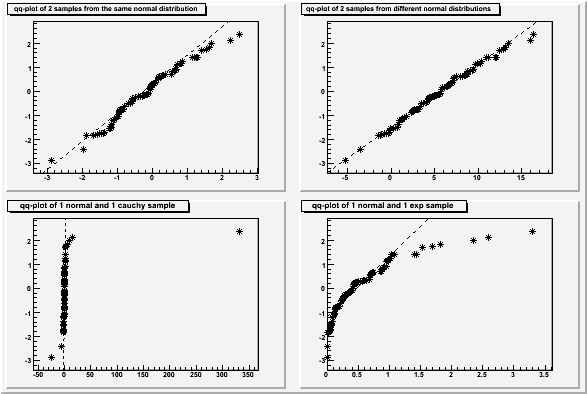 */
*/
 */
*/
