Chapter: Fitting Histograms

WARNING: This documentation is not maintained anymore. Some part might be obsolete or wrong, some part might be missing but still some valuable information can be found there. Instead please refer to the ROOT Reference Guide and the ROOT Manual. If you think some information should be imported in the ROOT Reference Guide or in the ROOT Manual, please post your request to the ROOT Forum or via a Github Issue.

7 Fitting Histograms

To fit a histogram you can use the Fit Panel on a visible histogram via the context menu, or you can use the TH1::Fit method. The Fit Panel, which is limited, is best for prototyping. The histogram needs to be drawn in a pad before the Fit Panel is invoked. The method TH1::Fit is more powerful and is used in scripts and programs.

7.1 The Fit Method

The Fit method is implemented in ROOT for the histogram classes TH1, the sparse histogram classes, THnSparse, the graph classes, TGraph, TGraph2D and TMultiGraph for fitting a collection of Graphs with the same function.

7.1.1 The TH1::Fit Method

To fit a histogram programmatically, you can use the TH1::Fit method. Here is the signatures of TH1::Fit and an explanation of the parameters:

   TFitResultPtr Fit(TF1 *function, Option_t *option, Option_t *goption,
            Axis_t xxmin, Axis_t  xxmax)

By default, the fitted function object is added to the histogram and is drawn in the current pad.

7.1.2 The TGraph::Fit Method

The signature for fitting a TGraph is exactly the same as for the TH1. Only some options apply only for fitting histograms, these are the options “L”, “WL” and “I”. These options apply instead only for TGraph::Fit, the rest of options (appart from “L”, “WL” and “I” are the same)

7.2 The TF1 function class

Here we will show how to create the TF1 class that is used for fitting histograms and graphs.

7.2.1 Fit with a Predefined Function

To fit a histogram with a predefined function, simply pass the name of the function in the first parameter of TH1::Fit. For example, this line fits histogram object hist with a Gaussian.

root[] hist.Fit("gaus");

The initial parameter values (and eventual limits) for pre-defined functions are set automatically. For overriding the default limits values use the fit option B.

The list of pre-defined functions that can be used with the Fit method is the following:

7.2.2 Creating User-Defined Functions (TF1)

You can create a TF1 object and use it in the call the TH1::Fit. The parameter in to the Fit method is the NAME of the TF1 object. There are three ways to create a TF1.

7.2.2.1 Creating a TF1 with a Formula

Let’s look at the first case. Here we call the TF1 constructor by giving it the formula: sin(x)/x.

root[] TF1  *f1 = new TF1("f1","sin(x)/x",0,10)

You can also use a TF1 object in the constructor of another TF1.

root[] TF1  *f2 = new TF1("f2","f1*2",0,10)

7.2.2.2 Creating a TF1 with Parameters

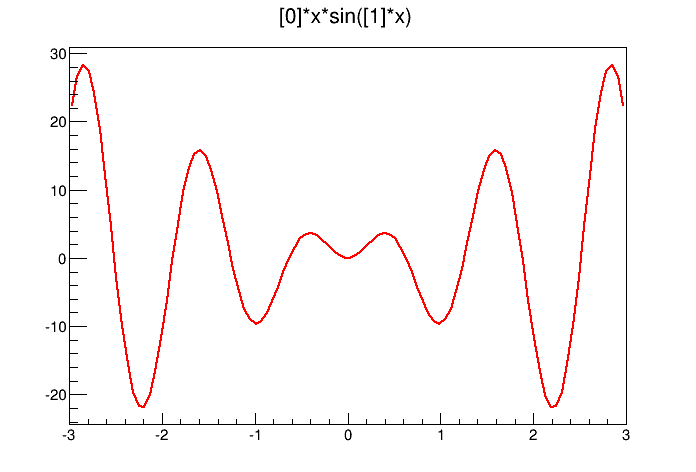
The second way to construct a TF1 is to add parameters to the expression. Here we use two parameters:

root[] TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
The function x*sin(x)
The function x*sin(x)

The parameter index is enclosed in square brackets. To set the initial parameters explicitly you can use:

root[] f1->SetParameter(0,10);

This sets parameter 0 to 10. You can also use SetParameters to set multiple parameters at once.

root[] f1->SetParameters(10,5);

This sets parameter 0 to 10 and parameter 1 to 5. We can now draw the TF1:

root[] f1->Draw()

7.2.2.3 Creating a TF1 with a User Function

The third way to build a TF1 is to define a function yourself and then pass the function pointer to the constructor. A function for a TF1 constructor needs to have this exact signature:

Double_t fitf(Double_t *x,Double_t *par)

The two parameters are:

The following script $ROOTSYS/tutorials/fit/myfit.C illustrates how to fit a 1D histogram with a user-defined function. First we declare the function.

   // define a function with 3 parameters
   Double_t fitf(Double_t *x,Double_t *par) {
      Double_t arg = 0;
      if (par[2]!=0) arg = (x[0] - par[1])/par[2];
      Double_t fitval = par[0]*TMath::Exp(-0.5*arg*arg);
      return fitval;
   }

Now we use the function:

   // this function uses fitf to fit a histogram
   void fitexample() {

      // open a file and get a histogram
      TFile *f = new TFile("hsimple.root");
      TH1F *hpx = (TH1F*)f->Get("hpx");

      // Create a TF1 object using the function defined above.
      // The last three parameters specify the number of parameters
      // for the function.
      TF1 *func = new TF1("fit",fitf,-3,3,3);
      // set the parameters to the mean and RMS of the histogram
      func->SetParameters(500,hpx->GetMean(),hpx->GetRMS());

      // give the parameters meaningful names
      func->SetParNames ("Constant","Mean_value","Sigma");

      // call TH1::Fit with the name of the TF1 object
      hpx->Fit("fit");
   }

You can create a TF1 also from a C++ function object (functor) with parameters A TF1 can be created from any C++ class implementing this member function:

double operator()(double *x, double *p)

The advantage of the function object is that it can have a state and reference therefore what-ever other object the user needs, without using globals. This is an example to define first the function object

class  MyFunctionObject {
 public:
  // use constructor to customize your function object
  MyFunctionObject(......) { ......}

   double operator() (double *x, double *p) {
      // function implementation using class data members
   }
};

and then use it to create the TF1:

   MyFunctionObject fobj(....);       // create the function object
   TF1 * f = new TF1("f",fobj,xmin,xmax,npar);    // create TF1 class with n-parameters and range [xmin,xmax]

If using C++11, one can create a TF1 also from a C++ lambda function:

// create TF1 class with 2 parameters and range [xmin,xmax] using a lambda
TF1 * f = new TF1("f",[](double*x,double*p){return p[0] + p[1]*x[0];},xmin,xmax,2);

7.3 Configuring the Fit

We will show here some configuration actions that can or must be done when fitting histogram or graph using the Fit method.

7.3.1 Fixing and Setting Parameters’ Bounds

Parameters must be initialized before invoking the Fit method. The setting of the parameter initial values is automatic for the predefined functions: poln, exp, gaus, and landau. You can fix one or more parameters by specifying the “B” option when calling the Fit method. When a function is not predefined, the fit parameters must be initialized to some value as close as possible to the expected values before calling the fit function.

To set bounds for one parameter, use TF1::SetParLimits:

   func->SetParLimits(0,-1,1);

When the lower and upper limits are equal, the parameter is fixed. Next two statements fix parameter 4 at 10.

   func->SetParameter(4,10);
   func->SetParLimits(4,10,10);

However, to fix a parameter to 0, one must call the FixParameter function:

   func->SetParameter(4,0);
   func->FixParameter(4,0);

Note that you are not forced to set the limits for all parameters. For example, if you fit a function with 6 parameters, you can:

   func->SetParameters(0,3.1,1.e-6,-1.5,0,100);
   func->SetParLimits(3,-10,4);
   func->FixParameter(4,0);

With this setup, parameters 0->2 can vary freely, parameter 3 has boundaries [-10, 4] with initial value -1.5, and parameter 4 is fixed to 0.

7.3.2 Fitting Sub Ranges

By default, TH1::Fit will fit the function on the defined histogram range. You can specify the option “R” in the second parameter of TH1::Fit to restrict the fit to the range specified in the TF1 constructor. In this example, the fit will be limited to -3 to 3, the range specified in the TF1 constructor.

root[] TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
root[] hist->Fit("f1","R");

You can also specify a range in the call to TH1::Fit:

root[] hist->Fit("f1","","",-2,2)

See macros $ROOTSYS/tutorials/fit/myfit.C and multifit.C as more completed examples.

7.3.3 Fitting Multiple Sub Ranges

The script for this example is $ROOTSYS/tutorials/fit/multifit.C. It shows how to use several Gaussian functions with different parameters on separate sub ranges of the same histogram. To use a Gaussian, or any other ROOT built in function, on a sub range you need to define a new TF1. Each is ‘derived’ from the canned function gaus.

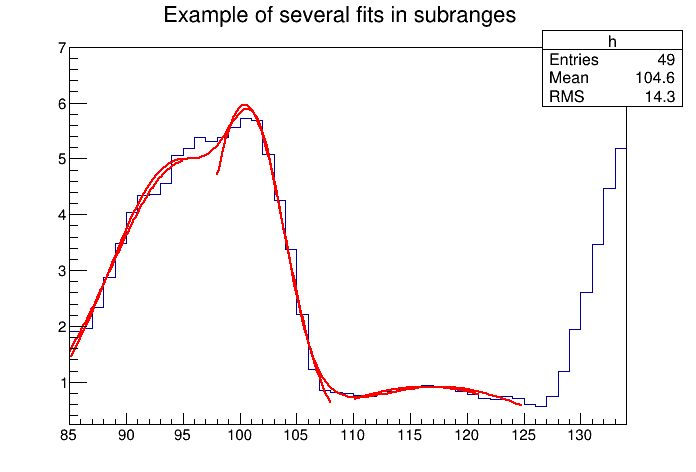
Fitting a histogram with several Gaussian functions
Fitting a histogram with several Gaussian functions

First, four TF1 objects are created - one for each sub-range:

   g1 = new TF1("m1","gaus",85,95);
   g2 = new TF1("m2","gaus",98,108);
   g3 = new TF1("m3","gaus",110,121);
   // The total is the sum of the three, each has 3 parameters
   total = new TF1("mstotal","gaus(0)+gaus(3)+gaus(6)",85,125);

Next, we fill a histogram with bins defined in the array x.

   // Create a histogram and set it's contents
   h = new TH1F("g1","Example of several fits in subranges",
                 np,85,134);
   h->SetMaximum(7);
   for (int i=0; i<np; i++) {
      h->SetBinContent(i+1,x[i]);
   }
   // Define the parameter array for the total function
   Double_t par[9];

When fitting simple functions, such as a Gaussian, the initial values of the parameters are automatically computed by ROOT. In the more complicated case of the sum of 3 Gaussian functions, the initial values of parameters must be set. In this particular case, the initial values are taken from the result of the individual fits. The use of the “+” sign is explained below:

   // Fit each function and add it to the list of functions
   h->Fit(g1,"R");
   h->Fit(g2,"R+");
   h->Fit(g3,"R+");

   // Get the parameters from the fit
   g1->GetParameters(&par[0]);
   g2->GetParameters(&par[3]);
   g3->GetParameters(&par[6]);

   // Use the parameters on the sum
   total->SetParameters(par);
   h->Fit(total,"R+");

7.3.4 Adding Functions to the List

The example $ROOTSYS/tutorials/fit/multifit.C also illustrates how to fit several functions on the same histogram. By default a Fit command deletes the previously fitted function in the histogram object. You can specify the option “+” in the second parameter to add the newly fitted function to the existing list of functions for the histogram.

root[] hist->Fit("f1","+","",-2,2)

Note that the fitted function(s) are saved with the histogram when it is written to a ROOT file.

7.4 Example of fit: Combining Functions

You can combine functions to fit a histogram with their sum as it is illustrated in the macro FitDemo.C ($ROOTSYS/tutorials/fit/FittingDemo.C). We have a function that is the combination of a background and Lorentzian peak. Each function contributes 3 parameters:

\[ y(E) = a_{1} + a_{2}E + a_{3}E^{2} + \frac{A_{p}(\frac{G}{2p})} {(E-m)^{2} + (\frac{G}{2})^2 } \]

BackgroundLorentzian Peak

par[0] = \(a_{1}\) par[0] = \(A_{p}\)

par[1] = \(a_{2}\) par[1] = \(G\)

par[2] = \(a_{3}\) par[2] = \(m\)

The combination function (fitFunction) has six parameters:

fitFunction = background(x,par) + LorentzianPeak(x,&par[3])

par[0]=\(a_{1}\) par[1]=\(a_{2}\) par[2]=\(a_{3}\) par[3]=\(A_{p}\) par[4]=\(G\) par[5]=\(m\)

This script creates a histogram and fits it with the combination of two functions. First we define the two functions and the combination function:

   // Quadratic background function
   Double_t background(Double_t *x, Double_t *par) {
      return par[0] + par[1]*x[0] + par[2]*x[0]*x[0];
   }

   // Lorentzian Peak function
   Double_t lorentzianPeak(Double_t *x, Double_t *par) {
      return (0.5*par[0]*par[1]/TMath::Pi()) / TMath::Max(1.e-10,
      (x[0]-par[2])*(x[0]-par[2])+ .25*par[1]*par[1]);
   }

   // Sum of background and peak function
   Double_t fitFunction(Double_t *x, Double_t *par) {
      return background(x,par) + lorentzianPeak(x,&par[3]);
   }

   void FittingDemo() {
   // bevington exercise by P. Malzacher, modified by R. Brun
   const int nBins = 60;
   Stat_t data[nBins] = {  6, 1,10,12, 6,13,23,22,15,21,
   23,26,36,25,27,35,40,44,66,81,
   75,57,48,45,46,41,35,36,53,32,
   40,37,38,31,36,44,42,37,32,32,
   43,44,35,33,33,39,29,41,32,44,
   26,39,29,35,32,21,21,15,25,15};
   TH1F *histo = new TH1F("example_9_1",
   "Lorentzian Peak on Quadratic Background",60,0,3);

   for(int i=0; i < nBins;  i++) {
      // we use these methods to explicitly set the content
      // and error instead of using the fill method.
      histo->SetBinContent(i+1,data[i]);
      histo->SetBinError(i+1,TMath::Sqrt(data[i]));
   }
   // create a TF1 with the range from 0 to 3 and 6 parameters
   TF1 *fitFcn = new TF1("fitFcn",fitFunction,0,3,6);

   // first try without starting values for the parameters
   // this defaults to 1 for each param.
   histo->Fit("fitFcn");
   // this results in an ok fit for the polynomial function however
   // the non-linear part (Lorentzian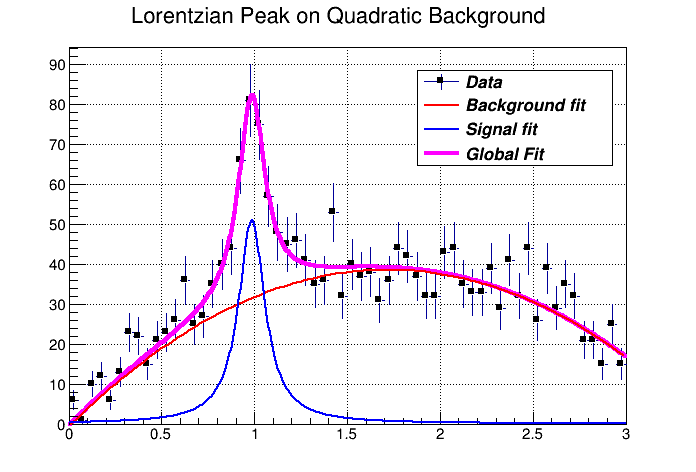
The output of the FittingDemo() example
The output of the FittingDemo() example

7.5 Result of the fit

Here we will show how to obtain the result of the fit (fitted function, parameter values, errors and eventually the covariance and correlation matrix).

7.5.1 Associated Function

One or more objects (typically a TF1\*) can be added to the list of functions (fFunctions) associated to each histogram. A call to TH1::Fit adds the fitted function to this list. Given a histogram h, one can retrieve the associated function with:

   TF1 *myfunc = h->GetFunction("myfunc");

7.5.2 Access to the Fit Parameters and Results

If the histogram (or graph) is made persistent, the list of associated functions is also persistent. Retrieve a pointer to the function with the TH1::GetFunction() method. Then you can retrieve the fit parameters from the function (TF1) with calls such as:

root[] TF1 *fit = hist->GetFunction(function_name);
root[] Double_t chi2 = fit->GetChisquare();
// value of the first parameter
root[] Double_t p1 = fit->GetParameter(0);
// error of the first parameter
root[] Double_t e1 = fit->GetParError(0);

Using the fit option S one can access the full result of the fit including the covariance and correlation matrix. See later the paragraph TFitResult.

7.5.3 Associated Errors

By default, for each bin, the sum of weights is computed at fill time. One can also call TH1::Sumw2 to force the storage and computation of the sum of the square of weights per bin. If Sumw2 has been called, the error per bin is computed as the sqrt(sum of squares of weights); otherwise, the error is set equal to the sqrt(bin content). To return the error for a given bin number, do:

   Double_t error = h->GetBinError(bin);

Empty bins are excluded in the fit when using the Chi-square fit method. When fitting an histogram representing counts (i.e with Poisson statistics) it is recommended to use the Log-Likelihood method (option ‘L’ or “WL”), particularly in case of low statistics. When the histogram has been filled with weights different than one, a weighted likelihood method can be used and the errors retrieved from the fit are corrected following a procedure described in paragraph 8.5.2 of the book, F. James, Statistical Methods in Experimental Physics, 2nd Edition.

7.5.4 Fit Statistics

You can change the statistics box to display the fit parameters with the TStyle::SetOptFit(mode) method. This parameter has four digits: mode = pcev (default = 0111)

For example, to print the fit probability, parameter names/values, and errors, use:

   gStyle->SetOptFit(1011);

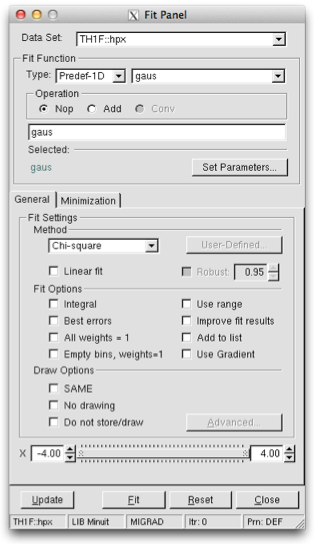
7.6 The Fit Panel

The Fit Panel
The Fit Panel

To display the Fit Panel right click on a histogram to pop up the context menu, and then select the menu entry Fit Panel.

The new Fit Panel GUI is available in ROOT v5.14. Its goal is to replace the old Fit Panel and to provide more user friendly way for performing, exploring and comparing fits.

By design, this user interface is planned to contain two tabs: “General” and “Minimization”. Currently, the “General” tab provides user interface elements for setting the fit function, fit method and different fit, draw, print options. The “Minimization tab” provides the option to set the Minimizer to use in the fit and its specific options.

The new fit panel is a modeless dialog, i.e. when opened, it does not prevent users from interacting with other windows. Its first prototype is a singleton application. When the Fit Panel is activated, users can select an object for fitting in the usual way, i.e. by left-mouse click on it. If the selected object is suitable for fitting, the fit panel is connected with this object and users can perform fits by setting different parameters and options.

7.6.1 Function Choice and Settings

‘Predefined’ combo box - contains a list of predefined functions in ROOT. You have a choice of several polynomials, a Gaussian, a Landau, and an Exponential function. The default one is Gaussian.

‘Operation’ radio button group defines the selected operational mode between functions:

Nop - no operation (default);

Add - addition;

Conv - convolution (will be implemented in the future).

Users can enter the function expression into the text entry field below the ‘Predefined’ combo box. The entered string is checked after the Enter key was pressed and an error message shows up, if the function string is not accepted.

‘Set Parameters’ button opens a dialog for parameters settings, which will be explained later.

7.6.2 Fitter Settings

‘Method’ combo box currently provides only two fit model choices: Chi-square and Binned Likelihood. The default one is Chi-square. The Binned Likelihood is recommended for bins with low statistics.

‘Linear Fit’ check button sets the use of Linear fitter when is selected. Otherwise the minimization is done by Minuit, i.e. fit option “F” is applied. The Linear fitter can be selected only for functions linear in parameters (for example - polN).

‘Robust’ number entry sets the robust value when fitting graphs.

‘No Chi-square’ check button switch On/Off the fit option “C” - do not calculate Chi-square (for Linear fitter).

‘Integral’ check button switch On/Off the option “I” - use integral of function instead of value in bin center.

‘Best Errors’ sets On/Off the option “E” - better errors estimation by using Minos technique.

‘All weights = 1’ sets On/Off the option “W”- all weights set to 1 excluding empty bins; error bars ignored.

‘Empty bins, weights=1’ sets On/Off the option “WW” - all weights equal to 1 including empty bins; error bars ignored.

‘Use range’ sets On/Off the option “R” - fit only data within the specified function range. Sliders settings are used if this option is set to On. Users can change the function range values by pressing the left mouse button near to the left/right slider edges. It is possible to change both values simultaneously by pressing the left mouse button near to the slider center and moving it to a new position.

‘Improve fit results’ sets On/Off the option “M”- after minimum is found, search for a new one.

‘Add to list’ sets On/Off the option “+”- add function to the list without deleting the previous one. When fitting a histogram, the function is attached to the histogram’s list of functions. By default, the previously fitted function is deleted and replaced with the most recent one, so the list only contains one function. Setting this option to On will add the newly fitted function to the existing list of functions for the histogram. Note that the fitted functions are saved with the histogram when it is written to a ROOT file. By default, the function is drawn on the pad displaying the histogram.

7.6.3 Draw Options

‘SAME’ sets On/Off function drawing on the same pad. When a fit is executed, the image of the function is drawn on the current pad.

‘No drawing’ sets On/Off the option “0”- do not draw the fit results.

‘Do not store/draw’ sets On/Off option “N”- do not store the function and do not draw it.

7.6.4 Advances Options

The advance option button is enabled only after having performed the fit and provides additional drawing options that can be used after having done the fit. These new drawing tools, which can be selected by the “Advanced Drawing Tool” panel that pops up when clicking the “Advanced” button, are:

This set of options specifies the amount of feedback printed on the root command line after performed fits.

‘Verbose’ - prints fit results after each iteration.

‘Quiet’ - no fit information is printed.

‘Default’ - between Verbose and Quiet.

7.6.6 Command Buttons

Fit button - performs a fit taking different option settings via the Fit Panel interface.

Reset - sets the GUI elements and related fit settings to the default ones.

Close - closes the Fit panel window.

7.6.7 Minimization Options

With this tab one can select specific options for minimization. These include

7.7 New ROOT::Fit classes

The fitting of the data objects in ROOT, histograms, graphs and tree is performed via some common classes, which are defined in the ROOT::Fit namespace. These classes can be classified in the following groups:

In addition the fitter classes make uses of the generic interfaces for parametric function evaluations, ROOT::Math::IParametricFunctionMultiDim to define the fit model function and use the ROOT::Math::Minimizer interface to perform the minimization of the objective function. More information about the function interface and the multi-dimensional minimization in ROOT is given in the Mathematical Library chapter.

Here we present a detailed description of the ROOT::Fit classes and how to use them. Using these classes instead of the interface provided directly in the ROOT data objects, like TH1::Fit allow are more fine control to configure and customise the fits. For example, using these classes a combined fit of several histograms can be performed.

To understand how these class work, let’s go through a simple example, such as fitting an histogram.

When fitting an histogram, instead of using TH1::Fit we will show in the following hot wo use the ROOT::Fit classes. We will show how to perform the following different type of fits with the histogram data: * a least square fit using the observed errors (Neyman chi-squared); * a least square fit using the expected errors from the function (Pearson chi-squared); * a binned likelihood fit; * an extended unbinned likelihood fits, if the histogram has been set to store in the buffer the original data used to fill it.

Let’s go through all the steps required for performing these fits using the ROOT::Fit::Fitter class. These steps are: 1. Create the input fit data object. 2. Create the input model function. 3. Configure the fit. 4. Perform the data fitting. 5. Examine the result.

7.7.1 Creating the input fit data

We have two types of input data, binned data (class ROOT::Fit::BinData) used for least square (chi-square) fits of histograms or TGraph objects or un-binned data (class ROOT::Fit::UnBinData) used for fitting vectors of data points (e.g. from a TTree).

7.7.1.1 Using Binned data

Let’s suppose we have an histogram, represented as a TH1 type object (it can be one or multi-dimensional). The following shows how to create and fill a ROOT:Fit::BinData object.

   ROOT::Fit::DataOptions opt;
   opt.fIntegral = true;
   ROOT::Fit::BinData data(opt);
   // fill the bin data using the histogram
   // we can do this using the following helper function from the Hist library
   TH1 * h1 = (TH1*) gDirectory->Get("myHistogram");
   ROOT::Fit::FillData(data, h1);

In this code example, we have used the utility function of the Hist library, ROOT::Fit::FillData to fill the BinData object. The ROOT::Fit::FillData is defined in the headerfile HFitInterface.h and it has a signature for all different ROOT objects, like TH1, THnBase, TGraph, TGraph2D and TMultiGraph It is possible to specify, when creating the BinData object, the data range we want to use and some fitting options we want to apply to fill in the object and later when fitting. The fit data options are controlled by the ROOT::Fit::DataOptions class, the range by the ROOT::Fit::DataRange class.

Here is an example how to specify the input option to use the integral of the function value in the bin instead of using the function value evaluated at the bin center, when doing the fit and to use a range beween the ‘xmin’ and ‘xmax’ values.

   ROOT::Fit::DataOptions opt;
   opt.fIntegral = true;
   ROOT::Fit::DataRange range(xmin,xmax);
   ROOT::Fit::BinData data(opt,range);
   // fill the bin data using the histogram
   // we can do this using the following helper function from the Hist library
   TH1 * h1 = (TH1*) gDirectory->Get("myHistogram");
   ROOT::Fit::FillData(data, h1);

The list of possible fit options available is the following:

   ROOT::Fit::DataOptions opt;
   opt.fIntegral = true;      // use integral of bin content instead of bin center (default is false).
   opt.fBinVolume = true;     // normalize data by the bin volume (default is false).
                              //  This is for fitting density functions in histograms with variable bin sizes.
   opt.fUseRange  =true;      // use the function range when creating the fit data (default is false).
   opt.fExpErrors = true;     // use the expected errors estimated from the function values
                              //  assuming Poisson statistics and not the observed errors (default is false).
   opt.fUseEmpty = true;      // use empty bins when fitting (default is false). If fExpErrors
                              //  is not set an arbitrary error = 1 is assigned to those bins.
   opt.fErrors1 = true;       // Set all measured errors to 1 (default is false).
   opt.fCoordErrors = false;  // When available coordinate errors are not used in the fit
                              //  (default is true: the errors are used when they are available,
                              //  e.g. fitting a TGraphErrors).
   opt.fAsymErrors = false;   // When available asymmetric errors are considered in the fit
                              //  (default is true, the asymmetric errors are used when they are available,
                              //  e.g. fitting a TGraphAsymmErrors).

The ROOT::Fit::DataRange class supports defining multiple rectangular ranges in each dimension, and supports n-dimension. The function DataRange::AddRange(icoord,xmin,xmax) adds a range in the coordinate icoord with lower value xmin and upper value xmax:

   ROOT::Fit::DataRange range;
   range.AddRange(icoordinate, xmin, xmax);

7.7.1.2 Using Un-Binned data

The unbinned data sets are represented with the ROOT::Fit::UnBinData class. For creating un-binned data sets, a ROOT::Fit::UnBinData object, one has two possibilities: 1. Copy the data inside ROOT::Fit::UnBinData. One can create an empty UnBinData object, iterate on the data and add the data point one by one, or directly create the UnBinData object from a data iterator. In this case an input ROOT::Fit::DataRange object is passed in order to copy the data according to the given range. 2. Use ROOT::Fit::UnBinData as a wrapper to an external data storage. In this case the UnBinData object is created from an iterator or pointers to the data and the data are not copied inside. In this case the data cannot be selected according to a specified range. All the data points will be included in the fit.

The ROOT::Fit::UnBinData class supports also weighted data. In addition to the data points (coordinates), which can be of arbitrary k dimensions, the class can be constructed from a vector of weights. This is an example of taking data from an histogram buffer of a TH1 object:

    double * buffer = histogram->GetBuffer();
    // number of entry is first entry in the buffer
    int n = buffer[0];
    // when creating the data object it is important to create with the size of the data
    ROOT::Fit::UnBinData data(n);
    for (int i = 0; i < n; ++i)
        data.add(buffer[2*i+1]);  // the buffer of 1D histogram contains nevt,x1,w1,x2,w2,......

Instead in this example we will create a 2-dim UnBinData object with the contents from a ROOT TTree

    TFile * file = TFile::Open("hsimple.root");
    TTree *ntuple = 0; file->GetObject("ntuple",ntuple);
    // select from the tree the data we want to use for fitting
    // we use TTree::Draw  for this
    int nevt = ntuple->Draw("px:py","","goff");
    double * x = ntuple->GetV1();
    double * y = ntuple->GetV2();
    ROOT::Fit::UnBinData data(nevt, x, y );

7.7.2 Creating the Fit model

In order to fit a data sets we need a model to describe our data, e.g. a probability density function describing our observed data or an hypothetical function describing the relation between the independent variables X and the single dependent variable Y. We can have an arbitrary number k of independent variables. For example, when fitting a k-dimensional histogram, the independent variables X are the bin center coordinates and Y is the bin weight.

The model function needs to be expressed as function of some unknown parameters. The fitting will find the best parameter value to describe the observed data.

We can use the ROOT TF1 class, the parametric function class, to describe the model function. However the ROOT::Fit::Fitter class, to be independent of the ROOT Hist library, takes as input a more general parametric function object, the interface (abstract) class ROOT::Math::IParametricFunctionMultiDim, which describe a generic one or multi-dimensional function with parameters. This interface extends the abstract class ROOT::Math::IBaseFunctionMultiDim, with methods to set/retrieve parameter values and to evaluate the function given the independent vector of values X and vector of parameters P. More information about the different ROOT::Math function interfaces is available in the Mathematical Library chapter.

An end-user can convert a TF1 object in a ROOT::Math::IParametricFunctionMultiDim, using the wrapper class ROOT::Math::WrapperMultiTF1:

    TF1 * f1 = new TF1("f1","gaus");
    ROOT::Math::WrappedMultiTF1 fitFunction(f1, f1->GetNdim() );
    ROOT::Fit::Fitter fitter;
    fitter.SetFunction( fitFunction, false);

When creating the wrapper, the parameter values stored in TF1 will be copied in the ROOT::Math::WrappedMultiTF1 object. The function object representing the model function is given to the ROOT::Fitter class using the Fitter::SetFunction method.

The user has also the possibility to provide a function object, which implements the derivatives of the function with respect to the parameters. This information might be useful for some types of fits. In this case he needs to provide the function object as a class deriving from the ROOT::Math::IParametricGradFunctionMultiDim interface. Note that the wrapper class ROOT::Math::WrappedMultiTF1 implements also the gradient interface, using internally TF1::GradientPar, which is based on numerical differentiation, apart for the case of linear functions (i.e. when TF1::IsLinear() is true). The parameter derivatives of the model function can be useful to some minimization algorithms, such as Fumili. However, in general is better to leave the minimization algorithm (e.g. Minuit) to compute the needed derivatives using its own customised numerical differentiation algorithm. In order to not provide to the fitter the parameter derivatives, we explicitly passed in Fitter::SetFunction a false value.

7.7.3 Fit Configuration

The configuration of the fit is done via the ROOT::Fit::FitConfig class and its contained ROOT::Fit::ParameterSettings class. These are the possible allowed fit configurations:

The initial parameter values can be set directly in the input model function object. However, for setting parameter bounds and step sizes to values different than the automatically computed ones, one needs to use the ROOT::Fit::ParameterSetting class. This example code will set the lower/upper bounds for the first parameter and a lower bound for the second parameter

  fitter.SetFunction( fitFunction, false);
  fitter.Config().ParSettings(0).SetLimits(0,1.E6);
  fitter.Config().ParSettings(2).SetLowerLimit(0);

Note that a ROOT::Fit::ParameterSettings objects exists for each fit parameter and it created by the ROOT::Fit::FitConfig class, after the model function has been set in the Fitter. Only when the function is set, the number of parameter is known and automatically the FitConfig creates the corresponding ParameterSetting objects.

When fitting, different minimizer can be used. The can be implemented in different libraries and loaded ar run time by the plug-in manager system of ROOT. Each different minimizer (e.g. Minuit, Minuit2, Fumili, etc.) consists of a different implementation of the ROOT::Math::Minimizer interface. Within the same minimizer, thus within the same class implementing the Minimizer interface, different algorithms can exist. For example in the case of Minuit, we have Migrad, Simplex or Minimize. The minimizer and its corresponding algorithm, when available, can be set by using the function FitConfig::SetMinimizer("minimizerName") or by using directly the ROOT:Math::MinimizerOptions class.

If the requested minimizer is not available in ROOT, the default one is used. The default minimizer type and algorithm can be specified by using the static function ROOT::Math::MinimizerOptions::SetDefaultMinimizer("minimizerName")

7.7.4 Minimizer Libraries and Algorithms

The list of available minimizer libraries currently available in ROOT, with their corresponding available algorithms is the following one. Some minimizers (e.g. Minuit) contain several algorithms that the user can choose. Others are based on a single algorithm (e.g. Fumili)

Each minimizer can be configured using the ROOT::Math::MinimizerOptions class. The list of possible option that can be set are:

Note that not all the options are implemented by all the minimizers. For example in Minuit is possible to set the maximum number of function calls, but not the maximum number of iterations. The Strategy and the Precision options apply instead only for Minuit (and Minuit2).

The class supports also setting global default values for the options, by using the static functions MinimizerOptions::SetDefault... (for example MinimizerOptions::SetDefaultPrintLevel(int )). The static functions can be also used to set the minimizer options when using TH1::Fit or TGraph::Fit. The list of the current option values can be inspected by using MinimizerOptions::Print.

ROOT::Math::MinimizerOptions() opt;
// print the default minimizer option values
opt.Print();

In addition it is possible to provide extra options which might apply for a particular minimizer MinimizerOptions::SetExtraOptions(const IOptions & ). See the documentation of the particular minimizer to use for the list of possible additional options available.

7.7.5 Performing the Fit

Here we have now all the required input ingredients for the fit, the data and the function to fit. Depending on these we have now several different way to perform the fit, using the corresponding methods of the ROOT::Fit::Fitter class and depending on the type of input data.

7.7.5.1 Available fit methods

7.7.5.2 Customised Fit methods

Above we described the pre-defined methods used for fitting. A user can also implement its own fitting methods, thus its version of the chi-square or likelihood function he wants to minimize. In this case, the user does not really need to build as input a ROOT::Fit data set and model function as we described before. He can implements its own version of the method function using on its own data set objects and functions.

In this case ROOT::Fit::Fitter::SetFCN is used to set the method function and ROOT::Fit::FitFCN is used for fitting. The method function can be passed also in ROOT::Fit::FitFCN, but in this case a previously defined fitting configuration is used.

The possible type of method functions that are based in ROOT::Fit::Fitter::SetFCN are:

template <class Function>
bool Fitter::SetFCN(unsigned int npar, Function & f,
                    const double * initialParameters = 0,
                    unsigned int dataSize=0, bool isChi2Fit = false)
bool Fitter::SetFCN(const ROOT::Math::IBaseFunctionMultiDim  & f,
                    const double * initialParameters = 0,
                    unsigned int dataSize=0, bool isChi2Fit = false)
bool Fitter::SetFCN(const ROOT::Math::FitMethodFunction  & f,
                    const double * initialParameters = 0, unsigned int dataSize=0)
typedef void(* MinuitFCN)(int &npar, double *gin, double &f, double *u, int flag)
bool Fitter::SetFCN(MinuitFCN fcn, int npar,
                    const double * initialParameters = 0,
                    unsigned int dataSize=0, bool isChi2Fit = false)

7.7.6 Fit Result

The result of the fit is contained in the ROOT::Fit::Result object. A reference to the result object is obtained with the function Fitter::Result(). The ROOT::Fit::FitResult class provides an API for retrieving parameter values, errors, covariance and correlation matrix from the fit, minimum chi2/likelihood values, etc…

A FitResult::Print method is also available to print the result of the fit.

The class has a self-explanatory API so, see its reference documentation for the possible information available after the fit.

One extra functionality offered by ROOT::Fit::FitResult is the possibility to compute the confidence intervals of the function after the fit. The function ROOT::Fit::FitResult::GetConfidenceInterval given an input data sets (e.g. a BinData object) and a confidence level value (e.g. 68%) computes the lower/upper band values of the model function at the given data points.

7.7.7 TFitResult

TFitResult is a class deriving from ROOT::Fit::Result and providing in addition some convenient methods to return a covariance or correlation matrix as a TMatrixDSym object. In addition TFitResult derives from TNamed and can be conveniently stored in a file.

When fitting an histogram ( a TH1 object) or a graph (a TGraph object) it is possible to return a TFitResult via the TFitResultPtr object, which behaves as a smart pointer to a TFitResult. TFitResultPtr is the return object by TH1::Fit or TGraph::Fit. By default the TFitResultPtr contains only the status of the fit and can be obtained by an automatic conversion of the TFitResultPtr to an integer.

If the fit option S is instead used, TFitResultPtr contains the TFitResult and behaves as a smart pointer to it. This is an example:

int fitStatus =  hist->Fit(myFunction);   // TFitResultPtr contains only the fit status

TFitResultPtr r = hist->Fit(myFunction,"S");  // TFitResultPtr contains the TFitResult
TMatrixDSym cov = r->GetCovarianceMatrix();   //  to access the covariance matrix
Double_t chi2   = r->Chi2();                  // to retrieve the fit chi2
Double_t par0   = r->Parameter(0);            // retrieve the value for the parameter 0
Double_t err0   = r->ParError(0);             // retrieve the error for the parameter 0
r->Print("V");                                // print full information of fit including covariance matrix
r->Write();                                   // store the result in a file

7.8 The Minimization packages

As explained before various minimization packages can be used when fitting in ROOT. We have seen before how to configure the Fitter class to use different minimization packages and different minimization options. When using the Fit method the minimization package (and its options) can be selected using the static methods of the ROOT::Math::MinimizerOptions class. For example to select Minuit2 instead of Minuit for fitting an histogram do:

ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
// fit the histogram histo with the gaussian pre-defined function
histo->Fit("gaus");

In the following we will give some brief description of the minimization packages. The packages all implement the ROOT::Math::Minimizer interface which can be use for finding the minimum of a multi-dimensional function. The interface is documented in the Mathematical Library Chapter.

In addition packages like Minuit or Minuit2 provide their own interfaces.

7.9 MINUIT (Old TMInuit Version)

This package was originally written in FORTRAN by Fred James and part of PACKLIB (patch D506). It has been converted to a C++ class by René Brun. The current implementation in C++ is a straightforward conversion of the original FORTRAN version. The main changes are:

   h->Fit("gaus");
   gMinuit->Command("SCAn 1");
   TGraph *gr = (TGraph*)gMinuit->GetPlot();
   gr->SetMarkerStyle(21);
   gr->Draw("alp");
   gMinuit->SetGraphicsMode(kFALSE);

7.9.1 Basic Concepts of Minuit

The Minuit package acts on a multi parameter FORTRAN function to which one must give the generic name FCN. In the ROOT implementation, the function FCN is defined via the Minuit SetFCN member function when an histogram fitting is invoked. The value of FCN will in general depend on one or more variable parameters.

7.9.2 The Transformation of Limited Parameters

For variable parameters with limits, Minuit uses the following transformation:

Pint = arcsin(2((Pext-a)/(b-a))-1)

Pext = a+((b-a)/(2))(sinPint+1)

so that the internal value Pint can take on any value, while the external value Pext can take on values only between the lower limit a and the ext upper limit b. Since the transformation is necessarily non-linear, it would transform a nice linear problem into a nasty non-linear one, which is the reason why limits should be avoided if not necessary. In addition, the transformation does require some computer time, so it slows down the computation a little bit, and more importantly, it introduces additional numerical inaccuracy into the problem in addition to what is introduced in the numerical calculation of the FCN value. The effects of non-linearity and numerical round off both become more important as the external value gets closer to one of the limits (expressed as the distance to nearest limit divided by distance between limits). The user must therefore be aware of the fact that, for example, if they put limits of (0, 1010) on a parameter, then the values 0.0 and 1. 0 will be indistinguishable to the accuracy of most machines.

The transformation also affects the parameter error matrix, of course, so Minuit does a transformation of the error matrix (and the ‘’parabolic’’ parameter errors) when there are parameter limits. Users should however realize that the transformation is only a linear approximation, and that it cannot give a meaningful result if one or more parameters is very close to a limit, where \(\frac{\partial Pext}{\partial Pint} \neq 0\). Therefore, it is recommended that:

7.9.3 How to Get the Right Answer from Minuit

Minuit offers the user a choice of several minimization algorithms. The MIGRAD algorithm is in general the best minimized for nearly all functions. It is a variable-metric method with inexact line search, a stable metric updating scheme, and checks for positive-definiteness. Its main weakness is that it depends heavily on knowledge of the first derivatives, and fails miserably if they are very inaccurate.

If parameter limits are needed, in spite of the side effects, then the user should be aware of the following techniques to alleviate problems caused by limits:

7.9.3.1 Getting the Right Minimum with Limits

If MIGRAD converges normally to a point where no parameter is near one of its limits, then the existence of limits has probably not prevented Minuit from finding the right minimum. On the other hand, if one or more parameters is near its limit at the minimum, this may be because the true minimum is indeed at a limit, or it may be because the minimized has become ‘’blocked’’ at a limit. This may normally happen only if the parameter is so close to a limit (internal value at an odd multiple of \(\pm \frac{\pi}{2}\) that Minuit prints a warning to this effect when it prints the parameter values. The minimized can become blocked at a limit, because at a limit the derivative seen by the minimized \(\frac{\partial F}{\partial Pint}\) is zero no matter what the real derivative \(\frac{\partial F}{\partial Pext}\) is.

\[ \left(\frac{\partial F}{\partial Pint}\right) = \left(\frac{\partial F}{\partial Pext}\right) \left(\frac{\partial Pext}{\partial Pint}\right) = \left(\frac{\partial F}{\partial Pext}\right) = 0 \]

7.9.3.2 Getting the Right Parameter Errors with Limits

In the best case, where the minimum is far from any limits, Minuit will correctly transform the error matrix, and the parameter errors it reports should be accurate and very close to those you would have got without limits. In other cases (which should be more common, since otherwise you would not need limits), the very meaning of parameter errors becomes problematic. Mathematically, since the limit is an absolute constraint on the parameter, a parameter at its limit has no error, at least in one direction. The error matrix, which can assign only symmetric errors, then becomes essentially meaningless.

7.9.3.3 Interpretation of Parameter Errors

There are two kinds of problems that can arise: the reliability of Minuit’s error estimates, and their statistical interpretation, assuming they are accurate.

7.9.3.4 Statistical Interpretation

For discussion of basic concepts, such as the meaning of the elements of the error matrix, or setting of exact confidence levels see the articles:

7.9.4 Reliability of Minuit Error Estimates

Minuit always carries around its own current estimates of the parameter errors, which it will print out on request, no matter how accurate they are at any given point in the execution. For example, at initialization, these estimates are just the starting step sizes as specified by the user. After a HESSE step, the errors are usually quite accurate, unless there has been a problem. Minuit, when it prints out error values, also gives some indication of how reliable it thinks they are. For example, those marked CURRENT GUESS ERROR are only working values not to be believed, and APPROXIMATE ERROR means that they have been calculated but there is reason to believe that they may not be accurate.

If no mitigating adjective is given, then at least Minuit believes the errors are accurate, although there is always a small chance that Minuit has been fooled. Some visible signs that Minuit may have been fooled:

The best way to be absolutely sure of the errors is to use ‘’independent’’ calculations and compare them, or compare the calculated errors with a picture of the function. Theoretically, the covariance matrix for a ‘’physical’’ function must be positive-definite at the minimum, although it may not be so for all points far away from the minimum, even for a well-determined physical problem. Therefore, if MIGRAD reports that it has found a non-positive-definite covariance matrix, this may be a sign of one or more of the following:

7.9.4.1 A Non-physical Region

On its way to the minimum, MIGRAD may have traversed a region that has unphysical behavior, which is of course not a serious problem as long as it recovers and leaves such a region.

7.9.4.2 An Underdetermined Problem

If the matrix is not positive-definite even at the minimum, this may mean that the solution is not well defined, for example that there are more unknowns than there are data points, or that the parameterization of the fit contains a linear dependence. If this is the case, then Minuit (or any other program) cannot solve your problem uniquely. The error matrix will necessarily be largely meaningless, so the user must remove the under determinedness by reformulating the parameterization. Minuit cannot do this itself.

7.9.4.3 Numerical Inaccuracies

It is possible that the apparent lack of positive-definiteness is due to excessive round off errors in numerical calculations (in the user function), or not enough precision. This is unlikely in general, but becomes more likely if the number of free parameters is very large, or if the parameters are badly scaled (not all of the same order of magnitude), and correlations are large. In any case, whether the non-positive-definiteness is real or only numerical is largely irrelevant, since in both cases the error matrix will be unreliable and the minimum suspicious.

7.9.4.4 An Ill-posed Problem

For questions of parameter dependence, see the discussion above on positive-definiteness. Possible other mathematical problems are the following:

7.10 Minuit2 Package

Minuit2 is a new object-oriented implementation, written in C++, of the popular MINUIT minimization package. Compared with the TMinuit class, which is a direct conversion from FORTRAN to C++, Minuit2 is a complete redesign and re-implementation of the package. This new version provides all the functionality present in the old FORTRAN version, with almost equivalent numerical accuracy and computational performances. Furthermore, it contains some fixes and small improvements and this new functionality: * The possibility to set single side parameter limits * the FUMILI algorithm (see the next paragraph “FUMILI Minimization Package”), which is an optimized method for least square and log likelihood minimizations.

Minuit2 has been originally developed by M. Winkler and F. James in the SEAL project. More information can be found on the MINUIT Web Site and in particular at the following documentation page at http://www.cern.ch/minuit/doc/doc.html.

A detailed User Guide for Minuit2 exists, describing the API of the internal classes. ROOT uses Minuit2 for fitting via the Minuit2Minimizer class which implements the ROOT::Math::Minimizer interface.

Minuit2 is also distributed as an independent package of ROOT and can be built without any other dependency on the ROOT libraries.

Examples on how to use the Minuit2 and Fumili2 plug-ins are provided in the tutorials’ directory $ROOTSYS/tutorials/fit: minuit2FitBench.C, minuit2FitBench2D.C and minuit2GausFit.C. More information on the classes and functions present in Minuit2 is available at online reference documentation.

Useful information on MINUIT and minimization in general is provided in the following documents:

F. James, Minuit Tutorial on Function Minimization ( http://seal.cern.ch/documents/minuit/mntutorial.pdf); F. James, The Interpretation of Errors in Minuit ( http://seal.cern.ch/documents/minuit/mnerror.pdf);

7.11 FUMILI Minimization Package

FUMILI is used to minimize Chi-square function or to search maximum of likelihood function. Experimentally measured values \(F_{i}\) are fitted with theoretical functions \(f_{i}(\vec{x_{i}},\vec{\theta})\), where \(\vec{x_{i}}\) are coordinates, and \(\vec{\theta}\) - vector of parameters. For better convergence Chi-square function has to be the following form

\[ \frac{\chi^2}{2} = \frac{1}{2} \sum_{i=1}^{n} \left(\frac{f_{i}(\vec{x_{i}},\vec{\theta}) - F_{i}} {\sigma_{i}}\right)^{2} \]

where \(\sigma_{i}\) are errors of the measured function. The minimum condition is:

\[ \frac{\partial \chi^{2}}{\partial \theta_{i}} = \sum_{j=1}^{n} \frac{1}{\sigma_{j}^{2}} . \frac{\partial f_{i}}{\partial \theta_{i}} \left[ (\vec{x_{j}},\vec{\theta}) - F_{j}\right] = 0, i = 1 ... m \]

where \(m\) is the quantity of parameters. Expanding left part of this equation over parameter increments and retaining only linear terms one gets

\[ \left(\frac{\partial \chi^{2}}{\theta_{i}}\right) _{\theta = \vec{\theta}^{0}} + \sum_{k} \left(\frac{\partial^{2} \chi^{2}}{\partial \theta_{i} \partial \theta_{k}}\right) _{\theta = \vec{\theta}^{0}} . (\theta_{k} - \theta_{k}^{0}) = 0 \]

here \(\vec{\theta}^{0}\) is some initial value of parameters. In general case:

\[ {\frac{\partial^2\chi^2}{\partial\theta_i\partial\theta_k}}= \sum^n_{j=1}{\frac{1}{\sigma^2_j}} {\frac{\partial f_j}{\theta_i}} {\frac{\partial f_j}{\theta_k}} + \sum^n_{j=1}{\frac{(f_j - F_j)}{\sigma^2_j}}\cdot {\frac{\partial^2f_j}{\partial\theta_i\partial\theta_k}} \]

In FUMILI algorithm for second derivatives of Chi-square approximate expression is used when last term in previous equation is discarded. It is often done, not always wittingly, and sometimes causes troubles, for example, if user wants to limit parameters with positive values by writing down \(\theta_i^2\) instead of \(\theta_i\). FUMILI will fail if one tries minimize \(\chi^2 = g^2(\vec\theta)\) where g is arbitrary function.

Approximate value is:

\[ {\frac{\partial^2\chi^2}{\partial\theta_i\partial\theta_k}}\approx Z_{ik}= \sum^n_{j=1}{\frac{1}{\sigma^2_j}}{\frac{\partial f_j}{\theta_i}} {\frac{\partial f_j}{\theta_k}} \]

Then the equations for parameter increments are:

\[ \left(\frac{\partial\chi^2}{\partial\theta_i}\right)_ {\vec\theta={\vec\theta}^0} +\sum_k Z_{ik}\cdot(\theta_k-\theta^0_k) = 0, \qquad i=1\ldots m \]

Remarkable feature of algorithm is the technique for step restriction. For an initial value of parameter \({\vec\theta}^0\) a parallelepiped \(P_0\) is built with the center at \({\vec\theta}^0\) and axes parallel to coordinate axes \(\theta_i\). The lengths of parallelepiped sides along i-th axis is \(2b_i\), where \(b_i\) is such a value that the functions \(f_j(\vec\theta)\) are quasi-linear all over the parallelepiped.

FUMILI takes into account simple linear inequalities in the form:

\[ \theta_i^{min}\le\theta_i\le\theta^{max}_i\]

They form parallelepiped \(P\) (\(P_0\) may be deformed by \(P\)). Very similar step formulae are used in FUMILI for negative logarithm of the likelihood function with the same idea - linearization of function argument.

7.12 Neural Networks

7.12.1 Introduction

Neural Networks are used in various fields for data analysis and classification, both for research and commercial institutions. Some randomly chosen examples are image analysis, financial movements’ predictions and analysis, or sales forecast and product shipping optimization. In particles physics neural networks are mainly used for classification tasks (signal over background discrimination). A vast majority of commonly used neural networks are multilayer perceptrons. This implementation of multilayer perceptrons is inspired from the MLPfit package, which remains one of the fastest tools for neural networks studies.

7.12.2 The MLP

The multilayer perceptron is a simple feed-forward network with the following structure showed on the left.

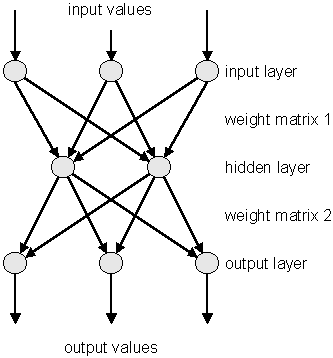
It is made of neurons characterized by a bias and weighted links in between - let’s call those links synapses. The input neurons receive the inputs, normalize them and forward them to the first hidden layer. Each neuron in any subsequent layer first computes a linear combination of the outputs of the previous layer. The output of the neuron is then function of that combination with f being linear for output neurons or a sigmoid for hidden layers.

Such a structure is very useful because of two theorems:

1- A linear combination of sigmoids can approximate any continuous function.

2- Trained with output=1 for the signal and 0 for the background, the approximated function of inputs X is the probability of signal, knowing X.

7.12.3 Learning Methods

The aim of all learning methods is to minimize the total error on a set of weighted examples. The error is defined as the sum in quadrate, divided by two, of the error on each individual output neuron. In all methods implemented in this library, one needs to compute the first derivative of that error with respect to the weights. Exploiting the well-known properties of the derivative, one can express this derivative as the product of the local partial derivative by the weighted sum of the outputs derivatives (for a neuron) or as the product of the input value with the local partial derivative of the output neuron (for a synapse). This computation is called “back-propagation of the errors”. Six learning methods are implemented.

7.12.3.1 Stochastic Minimization

This is the most trivial learning method. The Robbins-Monro stochastic approximation is applied to multilayer perceptrons. The weights are updated after each example according to the formula:

\[ w_{ij}(t+1) = w_{ij}(t) + \Delta w_{ij}(t) \]

with:

\[ \Delta w_{ij}(t) = - \eta \left( \frac{\partial e_p}{\partial w_{ij}} + \delta \right) + \epsilon \Delta w_{ij}(t-1) \]

The parameters for this method are Eta, EtaDecay, Delta and Epsilon.

7.12.3.2 Steepest Descent With Fixed Step Size (Batch Learning)

It is the same as the stochastic minimization, but the weights are updated after considering all the examples, with the total derivative dEdw. The parameters for this method are Eta, EtaDecay, Delta and Epsilon.

7.12.3.3 Steepest Descent Algorithm

Weights are set to the minimum along the line defined by the gradient. The only parameter for this method is Tau. Lower Tau = higher precision = slower search. A value Tau=3 seems reasonable.

7.12.3.4 Conjugate Gradients With the Polak-Ribiere Updating Formula

Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepest descent (estimated by using the Polak-Ribiere formula).

7.12.3.5 Conjugate Gradients With the Fletcher-Reeves Updating Formula

Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepest descent (estimated by using the Fletcher-Reeves formula).

7.12.3.6 The Broyden, Fletcher, Goldfarb, Shanno (BFGS) Method

It implies the computation of a NxN matrix, but seems more powerful at least for less than 300 weights. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepest descent.

7.12.4 Using the Network

Neural network are build from a set of “samples”. A sample is a set of values defining the inputs and the corresponding output that the network should ideally provide. In ROOT this is a TTree entry. The first thing to be decided is the network layout. This layout is described in a string where the layers are separated by semicolons. The input/output layers are defined by giving the expression for each neuron, separated by comas. Hidden layers are just described by the number of neurons.

In addition, input and output layer formulas can be preceded by ‘@’ (e.g. “@out”) if one wants to normalize the corresponding value. Also, if the string ends with ‘!’, output neurons are set up for classification, i.e. with a sigmoid (1 neuron) or softmax (more neurons) activation function.

Many questions on the good usage of neural network, including rules of dumb to determine the best network topology are addressed at ftp://ftp.sas.com/pub/neural/FAQ.html

   // a simple network: 2 inputs, 10 hidden and 1 normalized
   // output neuron
   TMultiLayerPerceptron network("r,z:10:@Br",tree);

Expressions are evaluated as for TTree::Draw(). Input and outputs are taken from the TTree associated with the network. This TTree can be given as argument of the constructor or defined later with TMultiLayerPerceptron::SetData(). Events can also be weighted. The weight expression can be given in the constructor or set later with the method SetWeight() of the class TMultiLayerPerceptron. Two datasets must be defined before learning the network: a training dataset that is used when minimizing the error, and a test dataset that will avoid bias. Those two datasets can be built aside and then given to the network, or can be built from a standard expression. By default, half of the events are put in both datasets.

   // a more complex 4:8:1 network
   // the ptsumf branch is used as weigh;
   // default event lists are explicit
   TMultiLayerPerceptron  network("m,pt,acol,acopl:8:type","pt",tree,
                                  "Entry$%2","Entry$/2");

The method TMultiLayerPerceptron::SetLearningMethod() defines the learning method. Learning methods are:

TMultiLayerPerceptron::kStochastic,
TMultiLayerPerceptron::kBatch,
TMultiLayerPerceptron::kSteepestDescent,
TMultiLayerPerceptron::kRibierePolak,
TMultiLayerPerceptron::kFletcherReeves,
TMultiLayerPerceptron::kBFGS      // default

The training can start with TMultiLayerPerceptron::Train(Int_t nepoch,Option_t* options). The first argument is the number of epochs while option is a string that can contain “text” (simple text output), “graph” (evaluating graphical training curves), “update = X” (step for the text/graph output update) or “+” (will skip the randomization and start from the previous values). All combinations are available.

   network.Train(1000,"text,graph,update=10"); // full output every
                                               // 10 epochs
   network.Train(100,"text,+");                // 100 more epochs
   //starts with existing weights

The weights can be saved to a file (DumpWeights) and then reloaded (LoadWeights) to a new compatible network. The output can also be evaluated (Evaluate) for a given output neuron and an array of double input parameters or the network can be exported (Export) as a standalone code. Up to now, this is only as a C++ or PYTHON class, but other languages could be implemented.

7.12.5 Examples

An example of how to use TMultiLayerPerceptron is the macro mlpHiggs.C in $ROOTSYS/tutorials. Using some standard simulated information that could have been obtained at LEP, a neural network is build, which can make the difference between WW events and events containing a Higgs boson. Starting with a TFile containing two TTrees: one for the signal, the other for the background, a simple script is used:

   void mlpHiggs(Int_t ntrain=100) {
      if (!gROOT->GetClass("TMultiLayerPerceptron"))
      gSystem->Load("libMLP");
      // prepare inputs - the 2 trees are merged into one, and a
      // "type" branch, equal to 1 for the signal and 0 for the
      // background is added
      TFile input("mlpHiggs.root");
      TTree *signal = (TTree *)input.Get("sig_filtered");
      TTree *background = (TTree *)input.Get("bg_filtered");
      TTree *simu = new TTree("MonteCarlo",
                              "Filtered Monte Carlo Events");
      ...

Since the input is a TTree and we are starting from two different TTrees (with different names), they are first merged into one, and a “type” branch is added, that says whether there is a signal or a background event. Those irrelevant details are skipped here.

      ...
      TMultiLayerPerceptron *mlp = new TMultiLayerPerceptron(
            "msumf,ptsumf, acolin, acopl:8:type","ptsumf",simu,
            "Entry$%2","Entry$/2");
      mlp->Train(ntrain, "text,graph,update=10");

The neural network is instantiated and trained. “ptsumf” is used as a weight, and the standard event lists are explicit. The network that is then build has four input neurons, eight additional ones in the only hidden layer and one single output neuron.

      // Use the NN to plot the results for each sample
      TH1F *bg = new TH1F("bgh","NN output",50,-.5,1.5);
      TH1F *sig = new TH1F("sigh","NN output",50,-.5,1.5);
      bg->SetDirectory(0);
      sig->SetDirectory(0);
      Double_t params[4];
      for (i = 0; i < background->GetEntries(); i++) {
         background->GetEntry(i);
         params[0] = msumf;    params[1] = ptsumf;
         params[2] = acolin;   params[3] = acopl;
         bg->Fill(mlp->Evaluate(0,params));
      }
      for (i = 0; i < signal->GetEntries(); i++) {
         signal->GetEntry(i);
         params[0] = msumf;
         params[1] = ptsumf;
         params[2] = acolin;
         params[3] = acopl;
         sig->Fill(mlp->Evaluate(0,params));
      }
      TCanvas *cv = new TCanvas("NNout_cv","Neural net output");
      bg->SetFillStyle(3008);
      bg->SetFillColor(kBlue);
      sig->SetFillStyle(3003);
      sig->SetFillColor(kRed);
      bg->SetStats(0);
      sig->SetStats(0);
      bg->Draw();
      sig->Draw("same");
      TLegend *legend = new TLegend(.75,.80,.95,.95);
      legend->AddEntry(bg,"Background(WW)");
      legend->AddEntry(sig,"Signal(Higgs)");
      legend->Draw();

The neural net output is then used to display the final difference between background and signal events. The figure “The neural net output” shows this plot.

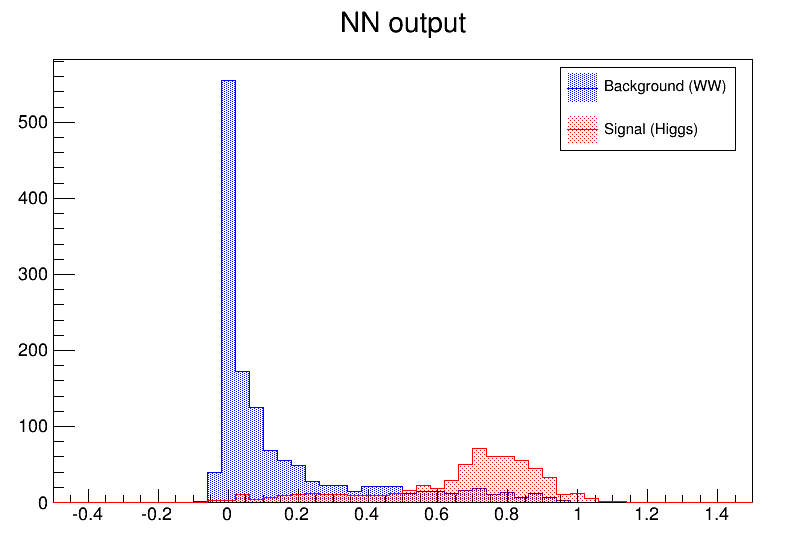
The neural net output
The neural net output

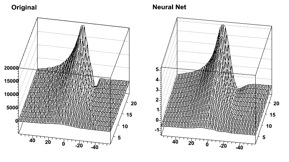
As it can be seen, this is a quite efficient technique. As mentioned earlier, neural networks are also used for fitting function. For some application with a cylindrical symmetry, a magnetic field simulation gives as output the angular component of the potential vector A, as well as the radial and z components of the B field.

One wants to fit those distributions with a function in order to plug them into the Geant simulation code. Polynomial fits could be tried, but it seems difficult to reach the desired precision over the full range. One could also use a spline interpolation between known points. In all cases, the resulting field would not be C-infinite.

An example of output (for Br) is shown. First the initial function can be seen as the target. Then, the resulting (normalized) neural net output. In order to ease the learning, the “normalize output” was used here. The initial amplitude can be recovered by multiplying by the original RMS and then shifting by the original mean.

The original and the neural net for Br
The original and the neural net for Br