 . Once
. Once 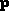 is rounded, the Remainder is exact, but the result is effectively phase shifted.
is rounded, the Remainder is exact, but the result is effectively phase shifted.
An alternative, supported in some systems but not by the CommonPoint application system, is to provide correctly rounded argument reduction modulo
Here, k is a small value like 2 or 3. As with the Remainder function, n is huge when x is. The implementation trick is to precompute
Using this technique, trigonometric functions have their correct period and large arguments aren't phase shifted. However, there is a performance penalty, especially for large arguments, compared to reduction with IEEE Remainder.
 . Given a floating-point value x, the idea is to compute n and r such that
. Given a floating-point value x, the idea is to compute n and r such that  .
.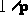 to thousands of bits of accuracy, so that the computation
to thousands of bits of accuracy, so that the computation 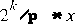 can be carried far enough (without error) to compute n and sufficiently many bits of
can be carried far enough (without error) to compute n and sufficiently many bits of  to recover r with just one rounding error.
to recover r with just one rounding error.
[Contents]
[Previous]
[Next]
![]() Click the icon to mail questions or corrections about this material to Taligent personnel.
Click the icon to mail questions or corrections about this material to Taligent personnel.