Processing /mnt/build/workspace/root-makedoc-v608/rootspi/rdoc/src/v6-08-00-patches/tutorials/fit/FittingDemo.C...
FCN=58.9284 FROM MIGRAD STATUS=CONVERGED 618 CALLS 619 TOTAL
EDM=1.54329e-09 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 1.2 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -8.64715e-01 8.87889e-01 3.02210e-05 -3.15277e-06
2 p1 4.58434e+01 2.64076e+00 6.35729e-04 1.78463e-05
3 p2 -1.33214e+01 9.77307e-01 -1.31737e-04 3.73302e-05
4 p3 1.38074e+01 2.20785e+00 -1.29864e-03 -9.22424e-06
5 p4 1.72308e-01 3.72077e-02 -5.22394e-06 -1.45631e-03
6 p5 9.87281e-01 1.13098e-02 2.92804e-06 -3.44378e-04
**********
** 10 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 p0 -8.64715e-01 8.87889e-01 no limits
2 p1 4.58434e+01 2.64076e+00 no limits
3 p2 -1.33214e+01 9.77307e-01 no limits
4 p3 1.38074e+01 2.20785e+00 no limits
5 p4 2.00000e-01 3.72077e-02 no limits
6 p5 1.00000e+00 1.13098e-02 no limits
**********
** 11 **SET ERR 1
**********
**********
** 12 **SET PRINT 2
**********
**********
** 13 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 14 **MIGRAD 1780 0.01
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-05
FCN=60.858 FROM MIGRAD STATUS=INITIATE 22 CALLS 23 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -8.64715e-01 8.87889e-01 8.87889e-01 4.29214e-01
2 p1 4.58434e+01 2.64076e+00 2.64076e+00 4.53155e-01
3 p2 -1.33214e+01 9.77307e-01 9.77307e-01 8.11696e-01
4 p3 1.38074e+01 2.20785e+00 2.20785e+00 -6.67494e-01
5 p4 2.00000e-01 3.72077e-02 3.72077e-02 5.35278e+01
6 p5 1.00000e+00 1.13098e-02 1.13098e-02 1.53279e+02
NO ERROR MATRIX
FCN=59.0986 FROM MIGRAD STATUS=PROGRESS 39 CALLS 40 TOTAL
EDM=0.770568 STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -9.13550e-01 8.87889e-01 -4.88344e-02 -1.02740e-01
2 p1 4.58158e+01 2.64076e+00 -2.75905e-02 -4.11668e-01
3 p2 -1.33297e+01 9.77307e-01 -8.26649e-03 -1.43164e+00
4 p3 1.43059e+01 2.20785e+00 4.98560e-01 3.34033e-01
5 p4 1.76669e-01 3.72077e-02 -2.33314e-02 -5.66279e+00
6 p5 9.90624e-01 1.13098e-02 -9.37641e-03 5.09250e+01
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
START COVARIANCE MATRIX CALCULATION.
EIGENVALUES OF SECOND-DERIVATIVE MATRIX:
1.2685e-02 2.6097e-01 6.2144e-01 1.0079e+00 1.5369e+00 2.5601e+00
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=58.9284 FROM HESSE STATUS=OK 40 CALLS 164 TOTAL
EDM=2.83537e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -8.62472e-01 8.91793e-01 2.08429e-03 4.68256e-04
2 p1 4.58294e+01 2.64212e+00 1.52471e-03 -1.63791e-03
3 p2 -1.33163e+01 9.76930e-01 6.23584e-04 6.32364e-03
4 p3 1.38135e+01 2.17742e+00 5.05443e-03 -2.23116e-04
5 p4 1.72389e-01 3.58301e-02 9.43447e-05 1.89644e-02
6 p5 9.87280e-01 1.12690e-02 4.24065e-05 -7.70600e-02
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5 6
1 0.78593 1.000 -0.512 0.400 -0.082 -0.117 0.042
2 0.98828 -0.512 1.000 -0.978 -0.526 -0.391 -0.061
3 0.98564 0.400 -0.978 1.000 0.545 0.410 0.053
4 0.78922 -0.082 -0.526 0.545 1.000 0.710 0.071
5 0.71738 -0.117 -0.391 0.410 0.710 1.000 0.070
6 0.09369 0.042 -0.061 0.053 0.071 0.070 1.000
FCN=58.9284 FROM MIGRAD STATUS=PROGRESS 176 CALLS 177 TOTAL
EDM=6.09404e-13 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -8.64713e-01 8.91793e-01 -2.24105e-03 1.85566e-07
2 p1 4.58434e+01 2.64212e+00 1.39273e-02 -9.90056e-09
3 p2 -1.33214e+01 9.76930e-01 -5.15131e-03 2.02571e-07
4 p3 1.38074e+01 2.17742e+00 -6.03314e-03 7.41648e-07
5 p4 1.72309e-01 3.58301e-02 -7.96940e-05 -2.58628e-05
6 p5 9.87281e-01 1.12690e-02 1.37418e-06 -8.42700e-05
MIGRAD MINIMIZATION HAS CONVERGED.
FCN=58.9284 FROM MIGRAD STATUS=CONVERGED 176 CALLS 177 TOTAL
EDM=6.09404e-13 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 0.0 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 -8.64713e-01 8.91794e-01 -2.24105e-03 1.85566e-07
2 p1 4.58434e+01 2.64221e+00 1.39273e-02 -9.90056e-09
3 p2 -1.33214e+01 9.76963e-01 -5.15131e-03 2.02571e-07
4 p3 1.38074e+01 2.17751e+00 -6.03314e-03 7.41648e-07
5 p4 1.72309e-01 3.58302e-02 -7.96940e-05 -2.58628e-05
6 p5 9.87281e-01 1.12690e-02 1.37418e-06 -8.42700e-05
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 6 ERR DEF=1
7.953e-01 -1.205e+00 3.484e-01 -1.594e-01 -3.729e-03 4.227e-04
-1.205e+00 6.981e+00 -2.525e+00 -3.027e+00 -3.704e-02 -1.812e-03
3.484e-01 -2.525e+00 9.545e-01 1.159e+00 1.434e-02 5.871e-04
-1.594e-01 -3.027e+00 1.159e+00 4.742e+00 5.537e-02 1.737e-03
-3.729e-03 -3.704e-02 1.434e-02 5.537e-02 1.284e-03 2.833e-05
4.227e-04 -1.812e-03 5.871e-04 1.737e-03 2.833e-05 1.270e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5 6
1 0.78593 1.000 -0.512 0.400 -0.082 -0.117 0.042
2 0.98828 -0.512 1.000 -0.978 -0.526 -0.391 -0.061
3 0.98564 0.400 -0.978 1.000 0.545 0.410 0.053
4 0.78924 -0.082 -0.526 0.545 1.000 0.710 0.071
5 0.71738 -0.117 -0.391 0.410 0.710 1.000 0.070
6 0.09364 0.042 -0.061 0.053 0.071 0.070 1.000
EXTERNAL ERROR MATRIX. NDIM= 6 NPAR= 6 ERR DEF=1
7.953e-01 -1.205e+00 3.484e-01 -1.594e-01 -3.729e-03 4.227e-04
-1.205e+00 6.981e+00 -2.525e+00 -3.027e+00 -3.704e-02 -1.812e-03
3.484e-01 -2.525e+00 9.545e-01 1.159e+00 1.434e-02 5.871e-04
-1.594e-01 -3.027e+00 1.159e+00 4.742e+00 5.537e-02 1.737e-03
-3.729e-03 -3.704e-02 1.434e-02 5.537e-02 1.284e-03 2.833e-05
4.227e-04 -1.812e-03 5.871e-04 1.737e-03 2.833e-05 1.270e-04
FCN=58.9284 FROM MIGRAD STATUS=CONVERGED 176 CALLS 177 TOTAL
EDM=6.09404e-13 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 0.0 per cent
EXT PARAMETER PARABOLIC MINOS ERRORS
NO. NAME VALUE ERROR NEGATIVE POSITIVE
1 p0 -8.64713e-01 8.91794e-01
2 p1 4.58434e+01 2.64221e+00
3 p2 -1.33214e+01 9.76963e-01
4 p3 1.38074e+01 2.17751e+00
5 p4 1.72309e-01 3.58302e-02
6 p5 9.87281e-01 1.12690e-02
return par[0] + par[1]*x[0] + par[2]*x[0]*x[0];
}
+ .25*par[1]*par[1]);
}
return background(x,par) + lorentzianPeak(x,&par[3]);
}
void FittingDemo() {
const int nBins = 60;
Double_t data[nBins] = { 6, 1,10,12, 6,13,23,22,15,21,
23,26,36,25,27,35,40,44,66,81,
75,57,48,45,46,41,35,36,53,32,
40,37,38,31,36,44,42,37,32,32,
43,44,35,33,33,39,29,41,32,44,
26,39,29,35,32,21,21,15,25,15};
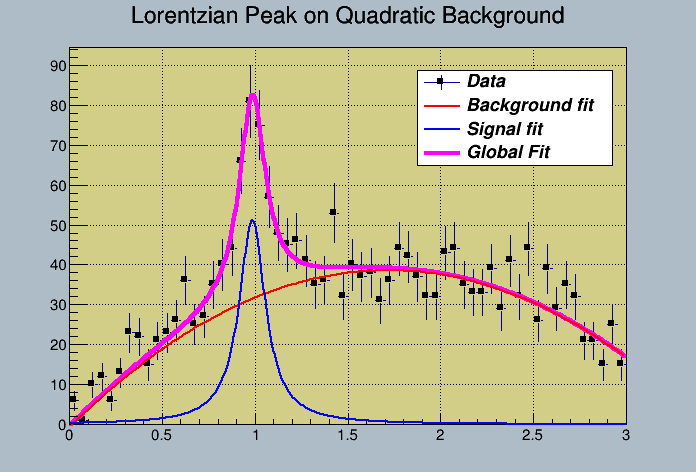
"Lorentzian Peak on Quadratic Background",60,0,3);
histo->
Fit(
"fitFcn",
"0");
histo->
Fit(
"fitFcn",
"V+",
"ep");
TF1 *backFcn =
new TF1(
"backFcn",background,0,3,3);
TF1 *signalFcn =
new TF1(
"signalFcn",lorentzianPeak,0,3,3);
legend->
AddEntry(backFcn,
"Background fit",
"l");
legend->
AddEntry(signalFcn,
"Signal fit",
"l");
legend->
AddEntry(fitFcn,
"Global Fit",
"l");
}



 Example for fitting signal/background.
Example for fitting signal/background.