#include <cmath>
struct GausND {
GausND( int dim ) :
{}
int k = 0;
for (int i = 0; i<dim; ++i) { X[i] = x[i] - p[k]; k++; }
for (int i = 0; i<dim; ++i) {
CovMat(i,i) = p[k]*p[k];
k++;
}
for (int i = 0; i<dim; ++i) {
for (int j = i+1; j<dim; ++j) {
CovMat(i,j) = p[k]*
sqrt(CovMat(i,i)*CovMat(j,j));
CovMat(j,i) = CovMat(i,j);
k++;
}
}
if (debug) {
}
if (det <= 0) {
Fatal(
"GausND",
"Determinant is <= 0 det = %f",det);
return 0;
}
if (debug) {
std::cout << "det " << det << std::endl;
std::cout << "norm " << norm << std::endl;
std::cout << "fval " << fval << std::endl;
}
return fval;
}
};
void multidimSampling() {
const int N = 10000;
const int DIM = 4;
double xmin[] = {-10,-10,-10, -10};
double xmax[] = { 10, 10, 10, 10};
double par0[] = { 1., -1., 2, 0,
1, 2, 1, 3,
0.5,0.,0.,0.,0.,0.8 };
const int NPAR = DIM + DIM*(DIM+1)/2;
GausND gaus4d(4);
TF1 * f =
new TF1(
"functionND",gaus4d,0,1,14);
double x0[] = {0,0,0,0};
debug = false;
for (int i = 0; i < NPAR; ++i ) {
if (i < DIM) f->
SetParName(i, name.Format(
"mu_%d",i+1) );
else if (i < 2*DIM) f->
SetParName(i, name.Format(
"sig_%d",i-DIM+1) );
else if (i < 2*DIM) f->
SetParName(i, name.Format(
"sig_%d",i-2*DIM+1) );
}
if (sampler == 0) {
Info(
"multidimSampling",
"Default sampler %s is not available try with Foam ",
}
sampler = Factory::CreateDistSampler();
if (sampler == 0) {
Error(
"multidimSampling",
"Foam sampler is not available - exit ");
return;
}
bool ret = sampler->
Init();
std::vector<double> data1(DIM*N);
double v[DIM];
if (!ret) {
Error(
"Sampler::Init",
"Error initializing unuran sampler");
return;
}
for (
int i = 0; i <
N; ++i) {
for (int j = 0; j < DIM; ++j)
data1[N*j + i] = v[j];
}
TFile * file = new TFile("multiDimSampling.root","RECREATE");
double x[DIM];
TTree * t1 = new TTree("t1","Tree from Unuran");
t1->Branch("x",x,"x[4]/D");
for (
int i = 0; i <
N; ++i) {
for (int j = 0; j < DIM; ++j) {
x[j] = data1[i+N*j];
}
t1->Fill();
}
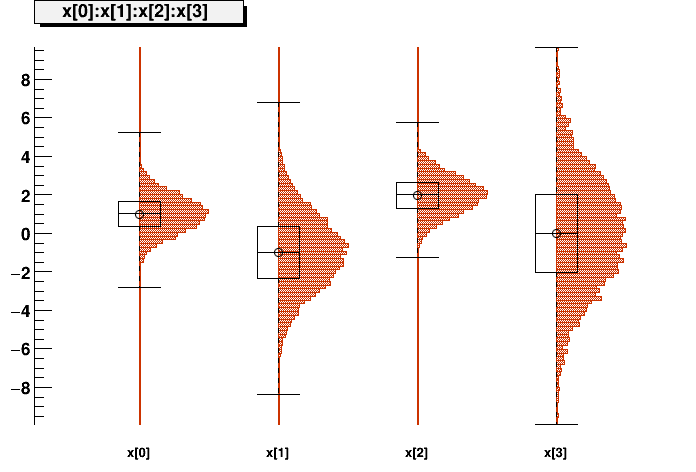
t1->Draw("x[0]:x[1]:x[2]:x[3]","","candle");
int ic=1;
t1->Write();
file->Close();
}



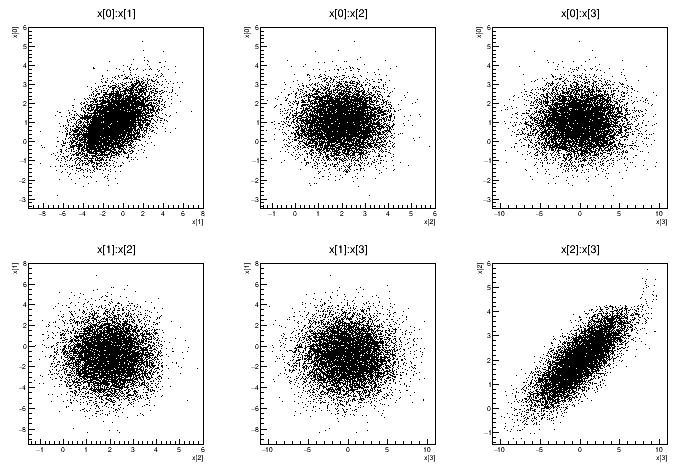
 Example of sampling a multi-dim distribution using the DistSampler class NOTE: This tutorial must be run with ACLIC
Example of sampling a multi-dim distribution using the DistSampler class NOTE: This tutorial must be run with ACLIC