fitLinearRobust.C File Reference

Detailed Description

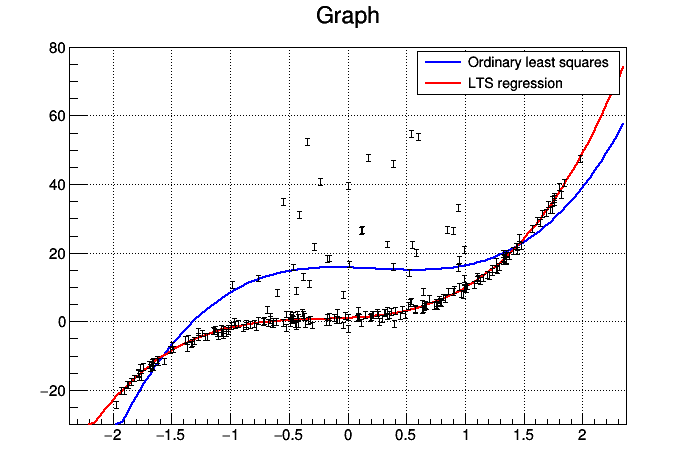
This tutorial shows how the least trimmed squares regression, included in the TLinearFitter class, can be used for fitting in cases when the data contains outliers.

Here the fitting is done via the TGraph::Fit function with option "rob": If you want to use the linear fitter directly for computing the robust fitting coefficients, just use the TLinearFitter::EvalRobust function instead of TLinearFitter::Eval

Processing /mnt/build/workspace/root-makedoc-v612/rootspi/rdoc/src/v6-12-00-patches/tutorials/fit/fitLinearRobust.C...
Ordinary least squares:

****************************************
Minimizer is Linear
Chi2                      =       606758
NDf                       =          246
p0                        =       15.724   +/-   0.0887641   
p1                        =    -0.835912   +/-   0.14096     
p2                        =     -3.40616   +/-   0.0607296   
p3                        =      4.82569   +/-   0.0602628   
Resistant Least trimmed squares fit:

****************************************
Minimizer is Linear / Robust (h=0.75)
Chi2                      =       634792
NDf                       =          246
p0                        =      1.00953
p1                        =      1.71148
p2                        =      2.97937
p3                        =      4.07752

#include "TRandom.h"
#include "TGraphErrors.h"
#include "TF1.h"
#include "TCanvas.h"
#include "TLegend.h"

void fitLinearRobust()
{
   //First generate a dataset, where 20% of points are spoiled by large
   //errors
   Int_t npoints = 250;
   Int_t fraction = Int_t(0.8*npoints);
   Double_t *x = new Double_t[npoints];
   Double_t *y = new Double_t[npoints];
   Double_t *e = new Double_t[npoints];
   TRandom r;
   Int_t i;
   for (i=0; i<fraction; i++){
      //the good part of the sample
      x[i]=r.Uniform(-2, 2);
      e[i]=1;
      y[i]=1 + 2*x[i] + 3*x[i]*x[i] + 4*x[i]*x[i]*x[i] + e[i]*r.Gaus();
   }
   for (i=fraction; i<npoints; i++){
      //the bad part of the sample
      x[i]=r.Uniform(-1, 1);
      e[i]=1;
      y[i] = 1 + 2*x[i] + 3*x[i]*x[i] + 4*x[i]*x[i]*x[i] + r.Landau(10, 5);
   }

   TGraphErrors *grr = new TGraphErrors(npoints, x, y, 0, e);
   grr->SetMinimum(-30);
   grr->SetMaximum(80);
   TF1 *ffit1 = new TF1("ffit1", "pol3", -5, 5);
   TF1 *ffit2 = new TF1("ffit2", "pol3", -5, 5);
   ffit1->SetLineColor(kBlue);
   ffit2->SetLineColor(kRed);
   TCanvas *myc = new TCanvas("myc", "Linear and robust linear fitting");
   myc->SetGrid();
   grr->Draw("ap");
   //first, let's try to see the result sof ordinary least-squares fit:
   printf("Ordinary least squares:\n");
   grr->Fit(ffit1);
   //the fitted function doesn't really follow the pattern of the data
   //and the coefficients are far from the real ones

   printf("Resistant Least trimmed squares fit:\n");
   //Now let's try the resistant regression
   //The option "rob=0.75" means that we want to use robust fitting and
   //we know that at least 75% of data is good points (at least 50% of points
   //should be good to use this algorithm). If you don't specify any number
   //and just use "rob" for the option, default value of (npoints+nparameters+1)/2
   //will be taken
   grr->Fit(ffit2, "+rob=0.75");
   //
   TLegend *leg = new TLegend(0.6, 0.8, 0.89, 0.89);
   leg->AddEntry(ffit1, "Ordinary least squares", "l");
   leg->AddEntry(ffit2, "LTS regression", "l");
   leg->Draw();

   delete [] x;
   delete [] y;
   delete [] e;

}

Author

Anna Kreshuk

Definition in file fitLinearRobust.C.