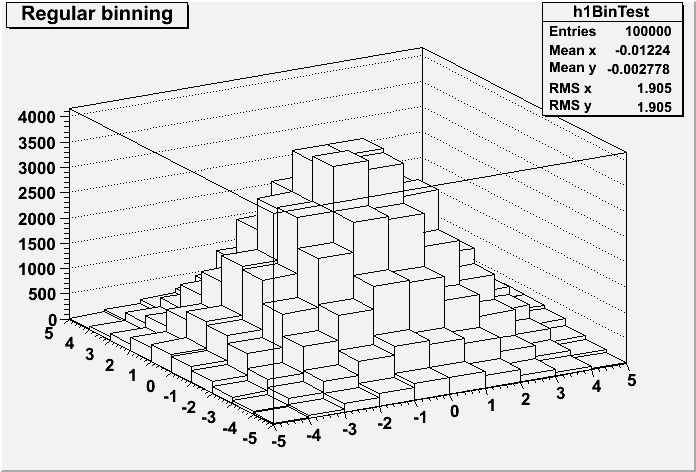
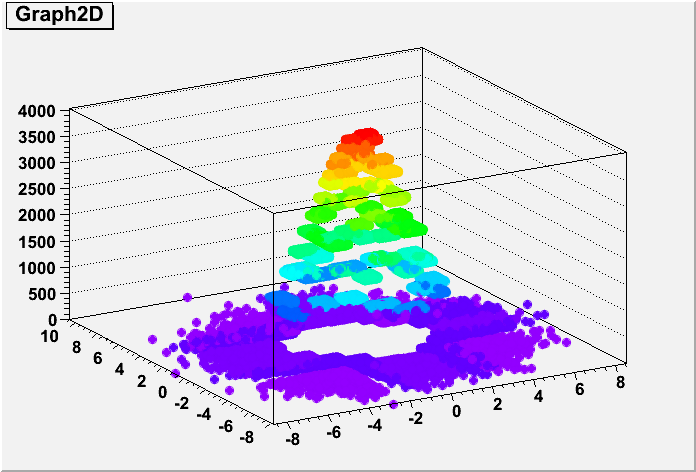
kdTreeBinning.C: kdTreeBinning tutorial: bin the data in cells of equal content using a kd-tree

// ------------------------------------------------------------------------
//
// kdTreeBinning tutorial: bin the data in cells of equal content using a kd-tree
//
// Using TKDTree wrapper class as a data binning structure
//  Plot the 2D data using the TH2Poly class
//
//
// Author:   Bartolomeu Rabacal    11/2010
//
// ------------------------------------------------------------------------

#include <math.h>

#include "TKDTreeBinning.h"
#include "TH2D.h"
#include "TH2Poly.h"
#include "TStyle.h"
#include "TGraph2D.h"
#include "TRandom3.h"
#include "TCanvas.h"
#include <iostream>

void kdTreeBinning() {

   // -----------------------------------------------------------------------------------------------
   //  C r e a t e  r a n d o m  s a m p l e  w i t h  r e g u l a r  b i n n i n g  p l o t t i n g
   // -----------------------------------------------------------------------------------------------

   const UInt_t DATASZ = 100000;
   const UInt_t DATADIM = 2;
   const UInt_t NBINS = 100;

   Double_t smp[DATASZ * DATADIM];

   TRandom3 r;
   r.SetSeed(1);
   for (UInt_t i = 0; i < DATADIM; ++i)
      for (UInt_t j = 0; j < DATASZ; ++j)
         smp[DATASZ * i + j] = r.Gaus(0., 2.);

   UInt_t h1bins = (UInt_t) sqrt(NBINS);

   TH2D* h1 = new TH2D("h1BinTest", "Regular binning", h1bins, -5., 5., h1bins, -5., 5.);
   for (UInt_t j = 0; j < DATASZ; ++j)
      h1->Fill(smp[j], smp[DATASZ + j]);

   TCanvas* c1 = new TCanvas("c1", "c1");
   c1->Update();
   c1->cd(1);

   h1->Draw("LEGO");

   // ---------------------------------------------------------------------------------------------
   // C r e a t e  K D T r e e B i n n i n g  o b j e c t  w i t h  T H 2 P o l y  p l o t t i n g
   // ---------------------------------------------------------------------------------------------

   TKDTreeBinning* fBins = new TKDTreeBinning(DATASZ, DATADIM, smp, NBINS);

   UInt_t nbins = fBins->GetNBins();
   UInt_t dim   = fBins->GetDim();

   const Double_t* binsMinEdges = fBins->GetBinsMinEdges();
   const Double_t* binsMaxEdges = fBins->GetBinsMaxEdges();

   gStyle->SetCanvasPreferGL(1);
   TH2Poly* h2pol = new TH2Poly("h2PolyBinTest", "KDTree binning", fBins->GetDataMin(0), fBins->GetDataMax(0), fBins->GetDataMin(1), fBins->GetDataMax(1));

   for (UInt_t i = 0; i < nbins; ++i) {
      UInt_t edgeDim = i * dim;
      h2pol->AddBin(binsMinEdges[edgeDim], binsMinEdges[edgeDim + 1], binsMaxEdges[edgeDim], binsMaxEdges[edgeDim + 1]);
   }

   for (UInt_t i = 1; i <= fBins->GetNBins(); ++i)
      h2pol->SetBinContent(i, fBins->GetBinDensity(i - 1));

   std::cout << "Bin with minimum density: " << fBins->GetBinMinDensity() << std::endl;
   std::cout << "Bin with maximum density: " << fBins->GetBinMaxDensity() << std::endl;

   TCanvas* c2 = new TCanvas("glc2", "c2");
   c2->Update();
   c2->cd(1);

   h2pol->Draw("gllego");

   /* Draw an equivalent plot showing the data points */
   /*-------------------------------------------------*/

   std::vector<Double_t> z = std::vector<Double_t>(DATASZ, 0.);
   for (UInt_t i = 0; i < DATASZ; ++i)
      z[i] = (Double_t) h2pol->GetBinContent(h2pol->FindBin(smp[i], smp[DATASZ + i]));

   TGraph2D *g = new TGraph2D(DATASZ, smp, &smp[DATASZ], &z[0]);
   gStyle->SetPalette(1);
   g->SetMarkerStyle(20);

   TCanvas* c3 = new TCanvas("c3", "c3");
   c3->Update();
   c3->cd(1);

   g->Draw("pcol");

   // ---------------------------------------------------------
   // R e b i n  t h e  K D T r e e B i n n i n g  o b j e c t
   // ---------------------------------------------------------

   fBins->SetNBins(200);

   TH2Poly* h2polrebin = new TH2Poly("h2PolyBinTest", "KDTree binning", fBins->GetDataMin(0), fBins->GetDataMax(0), fBins->GetDataMin(1), fBins->GetDataMax(1));
   h2polrebin->SetFloat();

   /* Sort the bins by their density  */
   /*---------------------------------*/

   fBins->SortBinsByDensity();

   for (UInt_t i = 0; i < fBins->GetNBins(); ++i) {
      const Double_t* binMinEdges = fBins->GetBinMinEdges(i);
      const Double_t* binMaxEdges = fBins->GetBinMaxEdges(i);
      h2polrebin->AddBin(binMinEdges[0], binMinEdges[1], binMaxEdges[0], binMaxEdges[1]);
   }

   for (UInt_t i = 1; i <= fBins->GetNBins(); ++i){
      h2polrebin->SetBinContent(i, fBins->GetBinDensity(i - 1));}

   std::cout << "Bin with minimum density: " << fBins->GetBinMinDensity() << std::endl;
   std::cout << "Bin with maximum density: " << fBins->GetBinMaxDensity() << std::endl;

   for (UInt_t i = 0; i < DATASZ; ++i)
      z[i] = (Double_t) h2polrebin->GetBin(h2polrebin->FindBin(smp[i], smp[DATASZ + i]));

   TCanvas* c4 = new TCanvas("glc4", "TH2Poly with kd-tree bin data",10,10,700,700);
   c4->Update();
   c4->Divide(1,2);
   c4->cd(1);
   h2polrebin->Draw("COLZ");  // draw as scatter plot

   c4->cd(2);
   h2polrebin->Draw("gllego");  // draw as lego

}