rs102_hypotestwithshapes.C: rs102_hypotestwithshapes for RooStats project

/////////////////////////////////////////////////////////////////
//
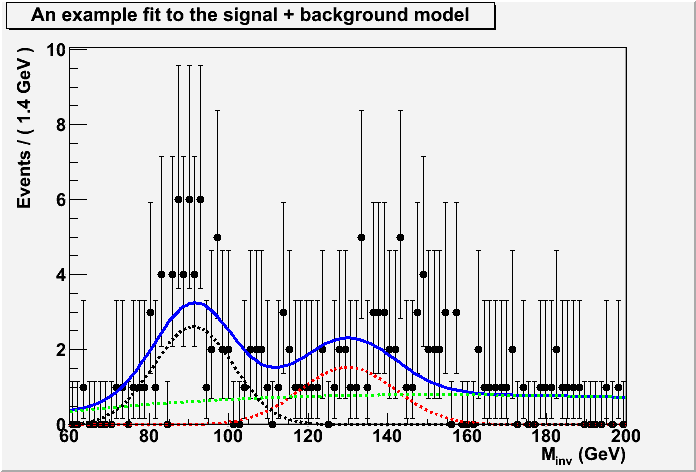
// rs102_hypotestwithshapes for RooStats project
// Author: Kyle Cranmer <cranmer@cern.ch>
// 
// Modified from version of February 29, 2008
//
// This tutorial macro shows a typical search for a new particle 
// by studying an invariant mass distribution.  
// The macro creates a simple signal model and two background models, 
// which are added to a RooWorkspace.
// The macro creates a toy dataset, and then uses a RooStats 
// ProfileLikleihoodCalculator to do a hypothesis test of the 
// background-only and signal+background hypotheses.
// In this example, shape uncertainties are not taken into account, but
// normalization uncertainties are.  
//
/////////////////////////////////////////////////////////////////

#ifndef __CINT__
#include "RooGlobalFunc.h"
#endif
#include "RooDataSet.h"
#include "RooRealVar.h"
#include "RooGaussian.h"
#include "RooAddPdf.h"
#include "RooProdPdf.h"
#include "RooAddition.h"
#include "RooProduct.h"
#include "TCanvas.h"
#include "RooChebychev.h"
#include "RooAbsPdf.h"
#include "RooFit.h"
#include "RooFitResult.h"
#include "RooPlot.h"
#include "RooAbsArg.h"
#include "RooWorkspace.h"
#include "RooStats/ProfileLikelihoodCalculator.h"
#include "RooStats/HypoTestResult.h"
#include <string>


// use this order for safety on library loading
using namespace RooFit;
using namespace RooStats;

// see below for implementation
void AddModel(RooWorkspace*);
void AddData(RooWorkspace*);
void DoHypothesisTest(RooWorkspace*);
void MakePlots(RooWorkspace*);

//____________________________________
void rs102_hypotestwithshapes() {

  // The main macro.

  // Create a workspace to manage the project.
  RooWorkspace* wspace = new RooWorkspace("myWS");

  // add the signal and background models to the workspace
  AddModel(wspace);

  // add some toy data to the workspace
  AddData(wspace);

  // inspect the workspace if you wish
  //  wspace->Print();

  // do the hypothesis test
  DoHypothesisTest(wspace);

  // make some plots
  MakePlots(wspace);

  // cleanup
  delete wspace;
}
 
//____________________________________
void AddModel(RooWorkspace* wks){

  // Make models for signal (Higgs) and background (Z+jets and QCD)
  // In real life, this part requires an intellegent modeling 
  // of signal and background -- this is only an example.  

  // set range of observable
  Double_t lowRange = 60, highRange = 200;

  // make a RooRealVar for the observable
  RooRealVar invMass("invMass", "M_{inv}", lowRange, highRange,"GeV");
 

  /////////////////////////////////////////////
  // make a simple signal model. 
  RooRealVar mH("mH","Higgs Mass",130,90,160) ; 
  RooRealVar sigma1("sigma1","Width of Gaussian",12.,2,100)  ;
  RooGaussian sigModel("sigModel", "Signal Model", invMass, mH, sigma1);
  // we will test this specific mass point for the signal
  mH.setConstant();
  // and we assume we know the mass resolution
  sigma1.setConstant();

  /////////////////////////////////////////////
  // make zjj model.  Just like signal model
  RooRealVar mZ("mZ", "Z Mass", 91.2, 0, 100);
  RooRealVar sigma1_z("sigma1_z","Width of Gaussian",10.,6,100)  ;
  RooGaussian zjjModel("zjjModel", "Z+jets Model", invMass, mZ, sigma1_z);
  // we know Z mass
  mZ.setConstant();
  // assume we know resolution too
  sigma1_z.setConstant();
  

  //////////////////////////////////////////////
  // make QCD model
  RooRealVar a0("a0","a0",0.26,-1,1) ; 
  RooRealVar a1("a1","a1",-0.17596,-1,1) ; 
  RooRealVar a2("a2","a2",0.018437,-1,1) ; 
  RooRealVar a3("a3","a3",0.02,-1,1) ; 
  RooChebychev qcdModel("qcdModel","A  Polynomail for QCD",invMass,RooArgList(a0,a1,a2)) ; 

  // let's assume this shape is known, but the normalization is not
  a0.setConstant();
  a1.setConstant();
  a2.setConstant();

  //////////////////////////////////////////////
  // combined model

  // Setting the fraction of Zjj to be 40% for initial guess.
  RooRealVar fzjj("fzjj","fraction of zjj background events",.4,0.,1) ; 

  // Set the expected fraction of signal to 20%.
  RooRealVar fsigExpected("fsigExpected","expected fraction of signal events",.2,0.,1) ; 
  fsigExpected.setConstant(); // use mu as main parameter, so fix this.

  // Introduce mu: the signal strength in units of the expectation.  
  // eg. mu = 1 is the SM, mu = 0 is no signal, mu=2 is 2x the SM
  RooRealVar mu("mu","signal strength in units of SM expectation",1,0.,2) ; 

  // Introduce ratio of signal efficiency to nominal signal efficiency. 
  // This is useful if you want to do limits on cross section.
  RooRealVar ratioSigEff("ratioSigEff","ratio of signal efficiency to nominal signal efficiency",1. ,0.,2) ; 
  ratioSigEff.setConstant(kTRUE);  

  // finally the signal fraction is the product of the terms above.
  RooProduct fsig("fsig","fraction of signal events",RooArgSet(mu,ratioSigEff,fsigExpected)) ; 

  // full model
  RooAddPdf model("model","sig+zjj+qcd background shapes",RooArgList(sigModel,zjjModel, qcdModel),RooArgList(fsig,fzjj)) ; 

  // interesting for debugging and visualizing the model
  //  model.printCompactTree("","fullModel.txt");
  //  model.graphVizTree("fullModel.dot");

  wks->import(model);
}

//____________________________________
void AddData(RooWorkspace* wks){
  // Add a toy dataset

  Int_t nEvents = 150;
  RooAbsPdf* model = wks->pdf("model");
  RooRealVar* invMass = wks->var("invMass");
 
  RooDataSet* data = model->generate(*invMass,nEvents);
  
  wks->import(*data, Rename("data"));

}

//____________________________________
void DoHypothesisTest(RooWorkspace* wks){


  // Use a RooStats ProfileLikleihoodCalculator to do the hypothesis test.
  ModelConfig model; 
  model.SetWorkspace(*wks);
  model.SetPdf("model");

  //plc.SetData("data");
 
  ProfileLikelihoodCalculator plc; 
  plc.SetData( *(wks->data("data") )); 

  // here we explicitly set the value of the parameters for the null.  
  // We want no signal contribution, eg. mu = 0
  RooRealVar* mu = wks->var("mu");
//   RooArgSet* nullParams = new RooArgSet("nullParams");
//   nullParams->addClone(*mu);
  RooArgSet poi(*mu);
  RooArgSet * nullParams = (RooArgSet*) poi.snapshot(); 
  nullParams->setRealValue("mu",0); 

  
  //plc.SetNullParameters(*nullParams);
  plc.SetModel(model);
  // NOTE: using snapshot will import nullparams 
  // in the WS and merge with existing "mu" 
  // model.SetSnapshot(*nullParams);
  
  //use instead setNuisanceParameters
  plc.SetNullParameters( *nullParams);

 

  // We get a HypoTestResult out of the calculator, and we can query it.
  HypoTestResult* htr = plc.GetHypoTest();
  cout << "-------------------------------------------------" << endl;
  cout << "The p-value for the null is " << htr->NullPValue() << endl;
  cout << "Corresponding to a signifcance of " << htr->Significance() << endl;
  cout << "-------------------------------------------------\n\n" << endl;


}

//____________________________________
void MakePlots(RooWorkspace* wks) {

  // Make plots of the data and the best fit model in two cases:
  // first the signal+background case
  // second the background-only case.

  // get some things out of workspace
  RooAbsPdf* model = wks->pdf("model");
  RooAbsPdf* sigModel = wks->pdf("sigModel");
  RooAbsPdf* zjjModel = wks->pdf("zjjModel");
  RooAbsPdf* qcdModel = wks->pdf("qcdModel");

  RooRealVar* mu = wks->var("mu");
  RooRealVar* invMass = wks->var("invMass");
  RooAbsData* data = wks->data("data");


  //////////////////////////////////////////////////////////
  // Make plots for the Alternate hypothesis, eg. let mu float

  mu->setConstant(kFALSE);

  model->fitTo(*data,Save(kTRUE),Minos(kFALSE), Hesse(kFALSE),PrintLevel(-1));
  
  //plot sig candidates, full model, and individual componenets
  new TCanvas();
  RooPlot* frame = invMass->frame() ; 
  data->plotOn(frame ) ; 
  model->plotOn(frame) ;   
  model->plotOn(frame,Components(*sigModel),LineStyle(kDashed), LineColor(kRed)) ;   
  model->plotOn(frame,Components(*zjjModel),LineStyle(kDashed),LineColor(kBlack)) ;   
  model->plotOn(frame,Components(*qcdModel),LineStyle(kDashed),LineColor(kGreen)) ;   
    
  frame->SetTitle("An example fit to the signal + background model");
  frame->Draw() ;
  //  cdata->SaveAs("alternateFit.gif");

  //////////////////////////////////////////////////////////
  // Do Fit to the Null hypothesis.  Eg. fix mu=0

  mu->setVal(0); // set signal fraction to 0
  mu->setConstant(kTRUE); // set constant 

  model->fitTo(*data, Save(kTRUE), Minos(kFALSE), Hesse(kFALSE),PrintLevel(-1));

  // plot signal candidates with background model and components
  new TCanvas();
  RooPlot* xframe2 = invMass->frame() ; 
  data->plotOn(xframe2, DataError(RooAbsData::SumW2)) ; 
  model->plotOn(xframe2) ; 
  model->plotOn(xframe2, Components(*zjjModel),LineStyle(kDashed),LineColor(kBlack)) ;   
  model->plotOn(xframe2, Components(*qcdModel),LineStyle(kDashed),LineColor(kGreen)) ;   
  
  xframe2->SetTitle("An example fit to the background-only model");
  xframe2->Draw() ;
  //  cbkgonly->SaveAs("nullFit.gif");

}