The physics vector classes describe vectors in three and four dimensions and their rotation algorithms. The classes were ported to root from CLHEP see:
http://wwwinfo.cern.ch/asd/lhc++/clhep/manual/UserGuide/Vector/vector.html
In order to use the physics vector classes you will have to load the Physics library:
gSystem.Load("libPhysics.so");There are four classes in this package. They are:
TVector3 is a general three-vector. A TVector3 may be expressed in Cartesian, polar, or cylindrical coordinates. Methods include dot and cross products, unit vectors and magnitudes, angles between vectors, and rotations and boosts. There are also functions of particular use to HEP, like pseudo-rapidity, projections, and transverse part of a TVector3, and kinetic methods on 4-vectors such as Invariant Mass of pairs or containers of particles.
TLorentzVector is a general four-vector class, which can be used either for the description of position and time (x, y, z, t) or momentum and energy (px, py, pz, E). TRotation is a class describing a rotation of a TVector3 object. TLorentzRotation is a class to describe the Lorentz transformations including Lorentz boosts and rotations. In addition, a TVector2 is a basic implementation of a vector in two dimensions and is not part of the CLHEP translation.

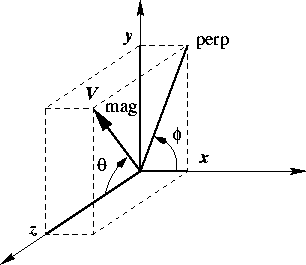
TVector3 is a general three-vector class, which can be used for description of different vectors in 3D. Components of three vectors:
\(x\), \(y\), \(z\) = basic components
\(\theta\) = azimuth angle
\(\phi\) = polar angle
magnitude = \(mag\) = \(\sqrt{x^2 + y^2 + z^2}\)
transverse component = \(perp\) = \(\sqrt{x^2 + y^2}\)
Using the TVector3 class, you should remember that it contains only common features of three vectors and lacks methods specific for some particular vector values. For example, it has no translated function because translation has no meaning for vectors.
TVector3 has been implemented as a vector of three Double_t variables, representing the Cartesian coordinates. By default the values are initialized to zero, however you can change them in the constructor:
TVector3 v1; // v1 = (0,0,0)
TVector3 v2(1); // v2 = (1,0,0)
TVector3 v3(1,2,3); // v3 = (1,2,3)
TVector3 v4(v2); // v4 = v2It is also possible (but not recommended) to initialize a TVector3 with a Double_t or Float_t C array. You can get the components by name or by index:
xx = v1.X(); or xx = v1(0);
yy = v1.Y(); yy = v1(1);
zz = v1.Z(); zz = v1(2);The methods SetX(), SetY(), SetZ() and SetXYZ() allow you to set the components:
v1.SetX(1.); v1.SetY(2.); v1.SetZ(3.);
v1.SetXYZ(1.,2.,3.);To get information on the TVector3 in spherical (rho, phi, theta) or cylindrical (z, r, theta) coordinates, the following methods can be used.
Double_t m = v.Mag();
// get magnitude (=rho=Sqrt(x*x+y*y+z*z)))
Double_t m2 = v.Mag2(); // get magnitude squared
Double_t t = v.Theta(); // get polar angle
Double_t ct = v.CosTheta();// get cos of theta
Double_t p = v.Phi(); // get azimuth angle
Double_t pp = v.Perp(); // get transverse component
Double_t pp2= v.Perp2(); // get transverse squaredIt is also possible to get the transverse component with respect to another vector:
Double_t ppv1 = v.Perp(v1);
Double_t pp2v1 = v.Perp2(v1);The pseudo-rapidity (eta = -ln (tan (theta/2))) can be obtained by Eta() or PseudoRapidity():
Double_t eta = v.PseudoRapidity();These setters change one of the non-Cartesian coordinates:
v.SetTheta(.5); // keeping rho and phi
v.SetPhi(.8); // keeping rho and theta
v.SetMag(10.); // keeping theta and phi
v.SetPerp(3.); // keeping z and phiThe TVector3 class has operators to add, subtract, scale and compare vectors:
v3 = -v1;
v1 = v2+v3;
v1 += v3;
v1 = v1 - v3;
v1 -= v3;
v1 *= 10;
v1 = 5*v2;
if(v1 == v2) {...}
if(v1 != v2) {...}v2 = v1.Unit(); // get unit vector parallel to v1
v2 = v1.Orthogonal(); // get vector orthogonal to v1s = v1.Dot(v2); // scalar product
s = v1 * v2; // scalar product
v = v1.Cross(v2); // vector productDouble_t a = v1.Angle(v2);v.RotateX(.5);
v.RotateY(TMath::Pi());
v.RotateZ(angle);v1.Rotate(TMath::Pi()/4, v2); // rotation around v2TVector3 objects can be rotated by TRotation objects using the Transform() method, the operator *=, or the operator * of the TRotation class. See the later section on TRotation.
TRotation m;
...
v1.Transform(m);
v1 = m*v1;
v1 *= m; // v1 = m*v1This code transforms v1 from the rotated frame (z’ parallel to direction, x’ in the theta plane and y’ in the xy plane as well as perpendicular to the theta plane) to the (x, y, z) frame.
TVector3 direction = v.Unit()
v1.RotateUz(direction); // direction must be TVector3 of unit lengthThe TRotation class describes a rotation of TVector3 object. It is a 3 * 3 matrix of Double_t:
\[\left| \begin{array}{ccc} xx & xy & xz \\ yx & yy & yz \\ zx & zy & zz \end{array} \right|\]
It describes a so-called active rotation, i.e. a rotation of objects inside a static system of coordinates. In case you want to rotate the frame and want to know the coordinates of objects in the rotated system, you should apply the inverse rotation to the objects. If you want to transform coordinates from the rotated frame to the original frame you have to apply the direct transformation. A rotation around a specified axis means counterclockwise rotation around the positive direction of the axis.
TRotation r; // r initialized as identity
TRotation m(r); // m = rThere is no direct way to set the matrix elements - to ensure that a TRotation always describes a real rotation. But you can get the values by with the methods XX()..ZZ() or the (,) operator:
Double_t xx = r.XX(); // the same as xx=r(0,0)
xx = r(0,0);
if (r==m) {...} // test for equality
if (r!=m) {..} // test for inequality
if (r.IsIdentity()) {...} // test for identityThe following matrices describe counter-clockwise rotations around the coordinate axes and are implemented in: RotateX(),RotateY() and RotateZ():
\[ Rx(a) = \left| \begin{array}{ccc} 1 & 0 & 0 \\ 0 & cos(a) & -sin(a) \\ 0 & sin(a) & cos(a) \end{array} \right| Ry(a) = \left| \begin{array}{ccc} cos(a) & 0 & sin(a) \\ 0 & 1 & 0 \\ -sin(a) & 0 & cos(a) \end{array} \right| Rz(a) = \left| \begin{array}{ccc} cos(a) & -sin(a) & 0 \\ sin(a) & cos(a) & 0 \\ 0 & 0 & 1 \end{array} \right| \]
r.RotateX(TMath::Pi()); // rotation around the x-axisThe Rotate() method allows you to rotate around an arbitrary vector (not necessary a unit one) and returns the result.
r.Rotate(TMath::Pi()/3,TVector3(3,4,5));It is possible to find a unit vector and an angle, which describe the same rotation as the current one:
Double_t angle;
TVector3 axis;
r.GetAngleAxis(angle,axis);The RotateAxes()method adds a rotation of local axes to the current rotation and returns the result:
TVector3 newX(0,1,0);
TVector3 newY(0,0,1);
TVector3 newZ(1,0,0);
a.RotateAxes(newX,newX,newZ);Methods ThetaX(), ThetaY(), ThetaZ(), PhiX(), PhiY(), PhiZ() return azimuth and polar angles of the rotated axes:
Double_t tx,ty,tz,px,py,pz;
tx= a.ThetaX();
...
pz= a.PhiZ(); TRotation a,b;
...
b = a.Inverse();// b is inverse of a, a is unchanged
b = a.Invert();// invert a and set b = aThe operator * has been implemented in a way that follows the mathematical notation of a product of the two matrices which describe the two consecutive rotations. Therefore, the second rotation should be placed first:
r = r2 * r1;The TRotation class provides an operator * which allows expressing a rotation of a TVector3 analog to the mathematical notation:
\[ \left| \begin{array}{c} x' \\ y' \\ z' \end{array} \right| = \left| \begin{array}{ccc} xx & xy & xz \\ yx & yy & yz \\ zx & zy & zz \end{array} \right| \times \left| \begin{array}{c} x \\ y \\ z \end{array} \right| \]
TRotation r;
TVector3 v(1,1,1);
v = r * v;You can also use the Transform() method or the operator *= of the TVector3 class:
TVector3 v;
TRotation r;
v.Transform(r);TLorentzVector is a general four-vector class, which can be used either for the description of position and time (x, y, z, t) or momentum and energy (px, py, pz, E).
TLorentzVector has been implemented as a set a TVector3 and a Double_t variable. By default, all components are initialized by zero.
TLorentzVector v1; // initialized by (0.,0.,0.,0.)
TLorentzVector v2(1.,1.,1.,1.);
TLorentzVector v3(v1);
TLorentzVector v4(TVector3(1.,2.,3.),4.);For backward compatibility there are two constructors from a Double_t and Float_t array.
There are two sets of access functions to the components of a TLorentzVector: X(), Y(), Z(), T() and Px(), Py(), Pz() and E(). Both sets return the same values but the first set is more relevant for use where TLorentzVector describes a combination of position and time and the second set is more relevant where TLorentzVector describes momentum and energy:
Double_t xx =v.X();
...
Double_t tt = v.T();
Double_t px = v.Px();
...
Double_t ee = v.E();The components of TLorentzVector can also accessed by index:
xx = v(0);orxx = v[0];
yy = v(1);yy = v[1];
zz = v(2);zz = v[2];
tt = v(3);tt = v[3];You can use the Vect() method to get the vector component of TLorentzVector:
TVector3 p = v.Vect();For setting components there are two methods: SetX(),.., SetPx(),..:
v.SetX(1.); orv.SetPx(1.);
......
v.SetT(1.);v.SetE(1.);To set more the one component by one call you can use the SetVect() function for the TVector3 part or SetXYZT(), SetPxPyPzE(). For convenience there is also a SetXYZM():
v.SetVect(TVector3(1,2,3));
v.SetXYZT(x,y,z,t);
v.SetPxPyPzE(px,py,pz,e);
v.SetXYZM(x,y,z,m); // v = (x,y,z,e = Sqrt(x*x+y*y+z*z+m*m))There are a couple of methods to get and set the TVector3 part of the parameters in spherical coordinate systems:
Double_t m, theta, cost, phi, pp, pp2, ppv2, pp2v2;
m = v.Rho();
t = v.Theta();
cost = v.CosTheta();
phi = v.Phi();
v.SetRho(10.);
v.SetTheta(TMath::Pi()*.3);
v.SetPhi(TMath::Pi());or get information about the r-coordinate in cylindrical systems:
Double_t pp, pp2, ppv2, pp2v2;
pp = v.Perp(); // get transverse component
pp2 = v.Perp2(); // get transverse component squared
ppv2 = v.Perp(v1); // get transverse component with respect
// to another vector
pp2v2 = v.Perp(v1);there are two more set functions SetPtEtaPhiE(pt,eta,phi,e) and SetPtEtaPhiM(pt,eta,phi,m) for convenience.
The TLorentzVector class provides operators to add subtract or compare four-vectors:
v3 = -v1;
v1 = v2+v3;
v1+= v3;
v1 = v2 + v3;
v1-= v3;
if (v1 == v2) {...}
if (v1 != v3) {...}The scalar product of two four-vectors is calculated with the (-,-,-,+)metric:
s = v1*v2 = t1*t2-x1*x2-y1*y2-z1*z2
The magnitude squared mag2 of a four-vector is therefore:
mag2 = v*v = t*t-x*x-y*y-z*z
If mag2 is negative: mag = -Sqrt(-mag*mag). The methods are:
Double_t s, s2;
s = v1.Dot(v2);// scalar product
s = v1*v2;// scalar product
s2 = v.Mag2();ors2 = v.M2();
s = v.Mag();s = v.M();Since in case of momentum and energy the magnitude has the meaning of invariant mass TLorentzVector provides the more meaningful aliases M2() and M(). The methods Beta() and Gamma() returns beta and gamma = 1/Sqrt(1-beta*beta).
A boost in a general direction can be parameterized with three parameters which can be taken as the components of a three vector b=(bx,by,bz). With x=(x,y,z) and gamma=1/Sqrt(1-beta*beta) (beta being the module of vector b), an arbitrary active Lorentz boost transformation (from the rod frame to the original frame) can be written as:
x = x' + (gamma-1)/(beta*beta)*(b*x')*b + gamma*t'*b
t = gamma(t'+ b*x')
The Boost() method performs a boost transformation from the rod frame to the original frame. BoostVector() returns a TVector3 of the spatial components divided by the time component:
TVector3 b;
v.Boost(bx,by,bz);
v.Boost(b);
b = v.BoostVector();// b=(x/t,y/t,z/t)There are four sets of functions to rotate the TVector3 component of a TLorentzVector:
Around Axes:
v.RotateX(TMath::Pi()/2.);
v.RotateY(.5);
v.RotateZ(.99);Around an arbitrary axis:
v.Rotate(TMath::Pi()/4., v1); // rotation around v1Transformation from rotated frame:
v.RotateUz(direction); // direction must be a unit TVector3Rotation by TRotation:
TRotation r;
v.Transform(r);//or v *= r; (v = r*v)Angle between two vectors:
Double_t a = v1.Angle(v2);// get angle between v1 and v2Methods Plus() and Minus() return the positive and negative light-cone components:
Double_t pcone = v.Plus();
Double_t mcone = v.Minus();A general Lorentz transformation (see class TLorentzRotation) can be used by the Transform() method, the *=, or * operator of the TLorentzRotation class:
TLorentzRotation l;
v.Transform(l);
v = l*v;orv *= l;// v = l*vThe TLorentzRotation class describes Lorentz transformations including Lorentz boosts and rotations (see TRotation)
\[ lambda = \left| \begin{array}{cccc} xx & xy & xz & xt \\ yx & yy & yz & yt \\ zx & zy & zz & zt \\ tx & ty & tz & tt \end{array} \right| \]
By default it is initialized to the identity matrix, but it may also be initialized by other TLorentzRotation, by a pure TRotation or by a boost:
TLorentzRotation l; // l is initialized as identity
TLorentzRotation m(l);// m = l
TRotation r;
TLorentzRotation lr(r);
TLorentzRotation lb1(bx,by,bz);
TVector3 b;
TLorentzRotation lb2(b);The Matrix for a Lorentz boosts is:
\[ \left| \begin{array}{cccc} 1+gamma'*bx*bx & gamma'*bx*by & gamma'*bx*bz & gamma*bx \\ gamma'*bx*bz & 1+gamma'*by*by & gamma'*by*by & gamma*by \\ gamma'*bz*bx & gamma'*bz*by & 1+gamma'*bz*bz & gamma*bz \\ gamma*bx & gamma*by & gamma*bz & gamma \end{array} \right| \]
with the boost vector b=(bx,by,bz); gamma=1/Sqrt(1-beta*beta);gamma'=(gamma-1)/beta*beta.
The access to the matrix components is possible with the methods XX(), XY() … TT(), and with the operator(int,int):
Double_t xx;
TLorentzRotation l;
xx = l.XX(); // gets the xx component
xx = l(0,0); // gets the xx component
if (l == m) {...} // test for equality
if (l != m) {...} // test for inequality
if (l.IsIdentity()) {...} // test for identityThere are four possibilities to find the product of two TLorentzRotation transformations:
TLorentzRotation a,b,c;
c = b*a; // product
c = a.MatrixMultiplication(b); // a is unchanged
a *= b; // a=a*b
c = a.Transform(b) // a=b*a then c=aLorentz boosts:
Double_t bx, by, bz;
TVector3 v(bx,by,bz);
TLorentzRotation l;
l.Boost(v);
l.Boost(bx,by,bz);Rotations:
TVector3 axis;
l.RotateX(TMath::Pi()); // rotation around x-axis
l.Rotate(.5,axis); // rotation around specified vectorInverse transformation: use the method Inverse()to return the inverse transformation keeping the current one unchanged. The method Invert() inverts the current TLorentzRotation:
l1 = l2.Inverse(); // l1 is inverse of l2, l2 unchanged
l1 = l2.Invert(); // invert l2, then l1=l2The matrix for the inverse transformation of a TLorentzRotation is as follows:
\[ \left| \begin{array}{cccc} xx & xy & xz & -tx \\ yx & yy & yz & -ty \\ zx & zy & zz & -tz \\ -xt & -yt & -zt & tt \end{array} \right| \]
To apply TLorentzRotation to TLorentzVector you can use either the VectorMultiplication() method or the * operator. You can also use the Transform() function and the *=operator of the class TLorentzVector.
TLorentzVector v;
TLorentzRotation l;
...
v = l.VectorMultiplication(v);
v = l * v;
v.Transform(l);
v *= l; // v = l*vThe test file $ROOTSYS/test/TestVectors.cxx is an example of using physics vectors. The vector classes are not loaded by default, and to run it, you will need to load libPhysics.so first:
root[] .L $ROOTSYS/lib/libPhysics.so
root[] .x TestVectors.cxxTo load the physics vector library in a ROOT application use:
gSystem->Load("libPhysics");The example $ROOTSYS/test/TestVectors.cxx does not return much, especially if all went well, but when you look at the code you will find examples for many calls.