Detailed Description

Comparison of MCMC and PLC in a multi-variate gaussian problem

This tutorial produces an N-dimensional multivariate Gaussian with a non-trivial covariance matrix. By default N=4 (called "dim").

A subset of these are considered parameters of interest. This problem is tractable analytically.

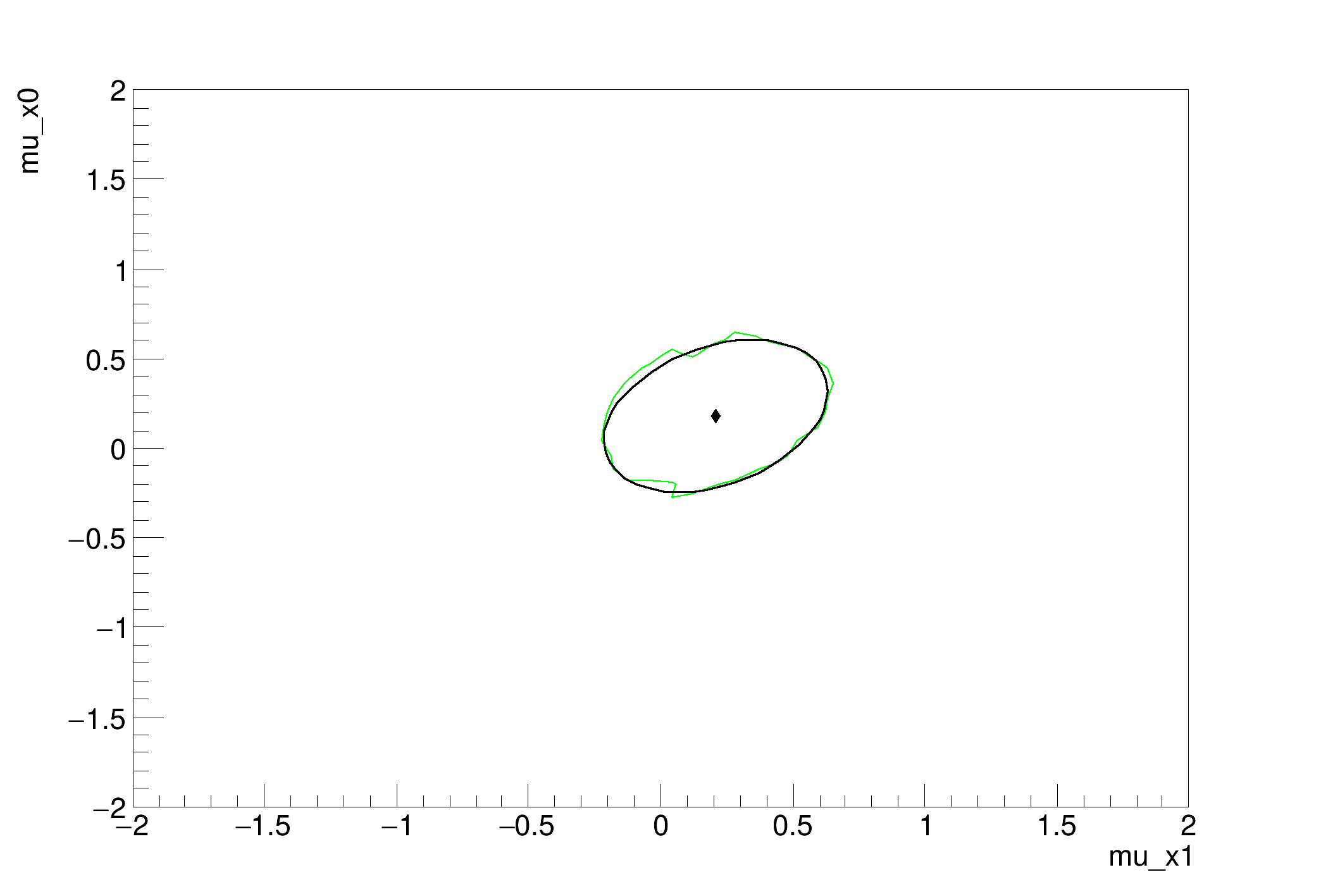
We use this mainly as a test of Markov Chain Monte Carlo and we compare the result to the profile likelihood ratio.

We use the proposal helper to create a customized proposal function for this problem.

For N=4 and 2 parameters of interest it takes about 10-20 seconds and the acceptance rate is 37%

[#1] INFO:Fitting -- RooAbsPdf::fitTo(mvg_over_mvg_Int[x0,x1,x2,x3]) fixing normalization set for coefficient determination to observables in data
[#1] INFO:Fitting -- using CPU computation library compiled with -mavx2
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_mvg_over_mvg_Int[x0,x1,x2,x3]_mvgData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
Minuit2Minimizer: Minimize with max-calls 2000 convergence for edm < 1 strategy 1
Minuit2Minimizer : Valid minimum - status = 0
FVAL  = 706.560063684865781
Edm   = 9.79361278577427602e-06
Nfcn  = 68
mu_x0   = 0.180728    +/-  0.17298  (limited)
mu_x1   = 0.207351    +/-  0.172978 (limited)
mu_x2   = -0.0159412  +/-  0.172984 (limited)
mu_x3   = 0.12343  +/-  0.172982 (limited)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:Fitting -- RooAbsPdf::fitTo(mvg_over_mvg_Int[x0,x1,x2,x3]) fixing normalization set for coefficient determination to observables in data
Metropolis-Hastings progress: ....................................................................................................
[#1] INFO:Eval -- Proposal acceptance rate: 37.1%
[#1] INFO:Eval -- Number of steps in chain: 3710
[#1] INFO:InputArguments -- The deprecated RooFit::CloneData(1) option passed to createNLL() is ignored.
[#1] INFO:Fitting -- RooAbsPdf::fitTo(mvg_over_mvg_Int[x0,x1,x2,x3]) fixing normalization set for coefficient determination to observables in data
[#0] PROGRESS:Minimization -- ProfileLikelihoodCalcultor::DoGLobalFit - find MLE 
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_mvg_over_mvg_Int[x0,x1,x2,x3]_mvgData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#0] PROGRESS:Minimization -- ProfileLikelihoodCalcultor::DoMinimizeNLL - using Minuit2 / Migrad with strategy 1
[#1] INFO:Minimization -- 
  RooFitResult: minimized FCN value: 706.56, estimated distance to minimum: 3.96149e-12
                covariance matrix quality: Full, accurate covariance matrix
                Status : MINIMIZE=0 
 
    Floating Parameter    FinalValue +/-  Error   
  --------------------  --------------------------
                 mu_x0    1.8118e-01 +/-  1.73e-01
                 mu_x1    2.0792e-01 +/-  1.73e-01
                 mu_x2   -1.6067e-02 +/-  1.73e-01
                 mu_x3    1.2371e-01 +/-  1.73e-01
 
[#1] INFO:Minimization -- RooProfileLL::evaluate(RooEvaluatorWrapper_Profile[mu_x1,mu_x0]) Creating instance of MINUIT
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_mvg_over_mvg_Int[x0,x1,x2,x3]_mvgData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooProfileLL::evaluate(RooEvaluatorWrapper_Profile[mu_x1,mu_x0]) determining minimum likelihood for current configurations w.r.t all observable
[#1] INFO:Minimization -- RooProfileLL::evaluate(RooEvaluatorWrapper_Profile[mu_x1,mu_x0]) minimum found at (mu_x0=0.181184, mu_x1=0.207918)
..[#1] INFO:Minimization -- LikelihoodInterval - Finding the contour of mu_x1 ( 1 ) and mu_x0 ( 0 ) 
Real time 0:00:02, CP time 2.490
MCMC interval on p0: [-0.19999999999999996, 0.6000000000000001]
MCMC interval on p1: [-0.28, 0.6000000000000001]

 
import ROOT
 
dim = 4
nPOI = 2
 
# let's time this challenging example
t = ROOT.TStopwatch()
t.Start()
 
xVec = []
muVec = []
poi = set()
 
# make the observable and means
for i in range(dim):
    name = "x{}".format(i)
    x = ROOT.RooRealVar(name, name, 0, -3, 3)
    xVec.append(x)
 
    mu_name = "mu_x{}".format(i)
    mu_x = ROOT.RooRealVar(mu_name, mu_name, 0, -2, 2)
    muVec.append(mu_x)
 
# put them into the list of parameters of interest
for i in range(nPOI):
    poi.add(muVec[i])
 
# make a covariance matrix that is all 1's
cov = ROOT.TMatrixDSym(dim)
for i in range(dim):
    for j in range(dim):
        if i == j:
            cov[i, j] = 3.0
        else:
            cov[i, j] = 1.0
 
# now make the multivariate Gaussian
mvg = ROOT.RooMultiVarGaussian("mvg", "mvg", xVec, muVec, cov)
 
# --------------------
# make a toy dataset
data = mvg.generate(xVec, 100)
 
# now create the model config for this problem
w = ROOT.RooWorkspace("MVG")
modelConfig = ROOT.RooStats.ModelConfig(w)
modelConfig.SetPdf(mvg)
modelConfig.SetParametersOfInterest(poi)
 
# -------------------------------------------------------
# Setup calculators
 
# MCMC
# we want to setup an efficient proposal function
# using the covariance matrix from a fit to the data
fit = mvg.fitTo(data, Save=True)
ph = ROOT.RooStats.ProposalHelper()
ph.SetVariables(fit.floatParsFinal())
ph.SetCovMatrix(fit.covarianceMatrix())
ph.SetUpdateProposalParameters(True)
ph.SetCacheSize(100)
pdfProp = ph.GetProposalFunction()
 
# now create the calculator
mc = ROOT.RooStats.MCMCCalculator(data, modelConfig)
mc.SetConfidenceLevel(0.95)
mc.SetNumBurnInSteps(100)
mc.SetNumIters(10000)
mc.SetNumBins(50)
mc.SetProposalFunction(pdfProp)
 
mcInt = mc.GetInterval()
poiList = mcInt.GetAxes()
 
# now setup the profile likelihood calculator
plc = ROOT.RooStats.ProfileLikelihoodCalculator(data, modelConfig)
plc.SetConfidenceLevel(0.95)
plInt = plc.GetInterval()
 
# make some plots
mcPlot = ROOT.RooStats.MCMCIntervalPlot(mcInt)
 
c1 = ROOT.TCanvas()
mcPlot.SetLineColor(ROOT.kGreen)
mcPlot.SetLineWidth(2)
mcPlot.Draw()
 
plPlot = ROOT.RooStats.LikelihoodIntervalPlot(plInt)
plPlot.Draw("same")
 
if len(poiList) == 1:
    p = poiList.at(0)
    print("MCMC interval: [{}, {}]".format(mcInt.LowerLimit(p), mcInt.UpperLimit(p)))
 
if len(poiList) == 2:
    p0 = poiList.at(0)
    p1 = poiList.at(1)
    scatter = ROOT.TCanvas()
    print("MCMC interval on p0: [{}, {}]".format(mcInt.LowerLimit(p0), mcInt.UpperLimit(p0)))
    print("MCMC interval on p1: [{}, {}]".format(mcInt.LowerLimit(p1), mcInt.UpperLimit(p1)))
 
    # MCMC interval on p0: [-0.2, 0.6]
    # MCMC interval on p1: [-0.2, 0.6]
 
    mcPlot.DrawChainScatter(p0, p1)
    scatter.Update()
    scatter.SaveAs("MultivariateGaussianTest_scatter.png")
 
t.Stop()
t.Print()
 
c1.SaveAs("MultivariateGaussianTest_plot.png")
 
# TODO: The MCMCCalculator has to be destructed first. Otherwise, we can get
# segmentation faults depending on the destruction order, which is random in
# Python. Probably the issue is that some object has a non-owning pointer to
# another object, which it uses in its destructor. This should be fixed either
# in the design of RooStats in C++, or with phythonizations.
del mc

Date: July 2022

Authors: Artem Busorgin, Kevin Belasco and Kyle Cranmer (C++ version)

Definition in file MultivariateGaussianTest.py.