rf105_funcbinding.py File Reference

Detailed Description

'BASIC FUNCTIONALITY' RooFit tutorial macro #105 Demonstration of binding ROOT Math functions as RooFit functions and pdfs

 
import ROOT
 
# Bind ROOT TMath::Erf C function
# ---------------------------------------------------
 
# Bind one-dimensional ROOT.TMath.Erf function as ROOT.RooAbsReal function
x = ROOT.RooRealVar("x", "x", -3, 3)
erf = ROOT.RooFit.bindFunction("erf", ROOT.TMath.Erf, x)
 
# Print erf definition
erf.Print()
 
# Plot erf on frame
frame1 = x.frame(Title="TMath.Erf bound as ROOT.RooFit function")
erf.plotOn(frame1)
 
# Bind ROOT::Math::beta_pdf C function
# -----------------------------------------------------------------------
 
# Bind pdf ROOT.Math.Beta with three variables as ROOT.RooAbsPdf function
x2 = ROOT.RooRealVar("x2", "x2", 0, 0.999)
a = ROOT.RooRealVar("a", "a", 5, 0, 10)
b = ROOT.RooRealVar("b", "b", 2, 0, 10)
beta = ROOT.RooFit.bindPdf("beta", ROOT.Math.beta_pdf, x2, a, b)
 
# Perf beta definition
beta.Print()
 
# Generate some events and fit
data = beta.generate({x2}, 10000)
beta.fitTo(data, PrintLevel=-1)
 
# Plot data and pdf on frame
frame2 = x2.frame(Title="ROOT.Math.Beta bound as ROOT.RooFit pdf")
data.plotOn(frame2)
beta.plotOn(frame2)
 
# Bind ROOT TF1 as RooFit function
# ---------------------------------------------------------------
 
# Create a ROOT TF1 function
fa1 = ROOT.TF1("fa1", "sin(x)/x", 0, 10)
 
# Create an observable
x3 = ROOT.RooRealVar("x3", "x3", 0.01, 20)
 
# Create binding of TF1 object to above observable
rfa1 = ROOT.RooFit.bindFunction(fa1, x3)
 
# Print rfa1 definition
rfa1.Print()
 
# Make plot frame in observable, TF1 binding function
frame3 = x3.frame(Title="TF1 bound as ROOT.RooFit function")
rfa1.plotOn(frame3)
 
c = ROOT.TCanvas("rf105_funcbinding", "rf105_funcbinding", 1200, 400)
c.Divide(3)
c.cd(1)
ROOT.gPad.SetLeftMargin(0.15)
frame1.GetYaxis().SetTitleOffset(1.6)
frame1.Draw()
c.cd(2)
ROOT.gPad.SetLeftMargin(0.15)
frame2.GetYaxis().SetTitleOffset(1.6)
frame2.Draw()
c.cd(3)
ROOT.gPad.SetLeftMargin(0.15)
frame3.GetYaxis().SetTitleOffset(1.6)
frame3.Draw()
 
c.SaveAs("rf105_funcbinding.png")

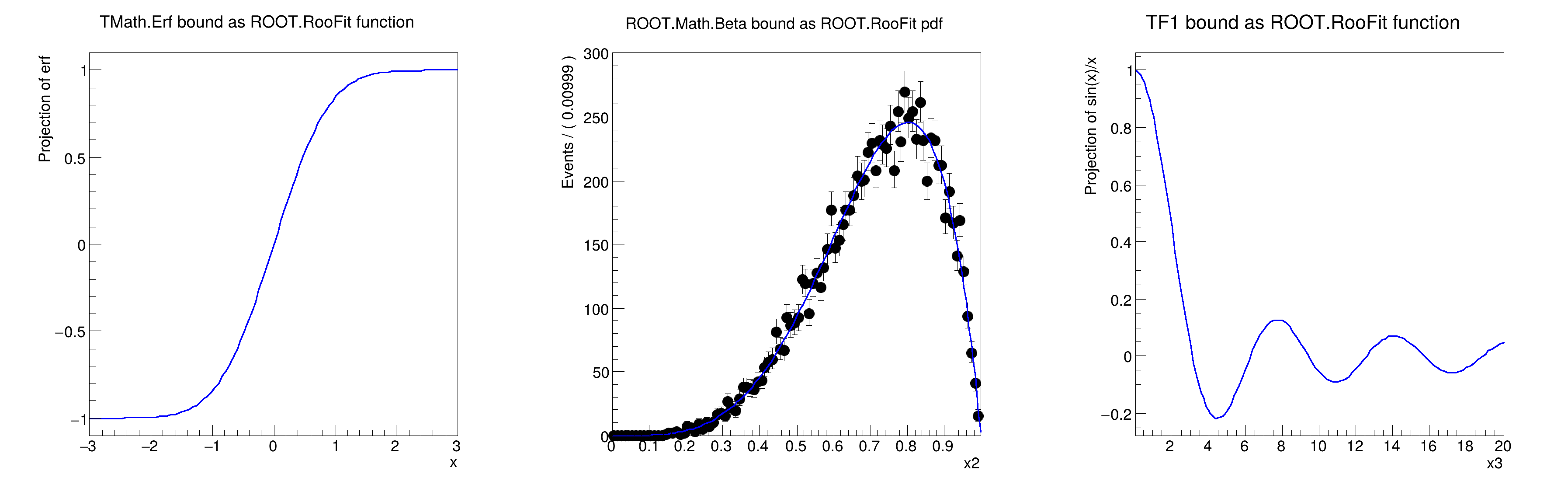
RooCFunction1Binding<double,double>::erf[ function=(0x7ff23b824000) x=x ] = 0
RooCFunction3PdfBinding<double,double,double,double>::beta[ function=ROOT::Math::beta_pdf x=x2 a=a b=b ] = 0.934689
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:Fitting -- RooAbsPdf::fitTo(beta_over_beta_Int[x2]) fixing normalization set for coefficient determination to observables in data
[#1] INFO:Fitting -- using CPU computation library compiled with -mavx2
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_beta_over_beta_Int[x2]_betaData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
RooTFnBinding::fa1[ TFn={fa1=sin(x)/x} obs=(x3) ] = -0.0547936

Date

February 2018

Authors

Clemens Lange, Wouter Verkerke (C version)

Definition in file rf105_funcbinding.py.