Logo ROOT   6.08/07
Reference Guide
portfolio.C File Reference
Tutorials » Quadratic programming package.

Detailed Description

View in nbviewer Open in SWAN This macro shows in detail the use of the quadratic programming package quadp .

Running this macro :

.x portfolio.C+

or

gSystem->Load("libQuadp");
.L portFolio.C+; portfolio()

Let's first review what we exactly mean by "quadratic programming" :

We want to minimize the following objective function :

\( c^T x + ( 1/2 ) x^T Q x \) wrt. the vector \( x \)

\( c \) is a vector and \( Q \) a symmetric positive definite matrix

You might wonder what is so special about this objective which is quadratic in the unknowns, that can not be done by Minuit/Fumili . Well, we have in addition the following boundary conditions on \( x \):

\[ A x = b \\ clo \le C x \le cup \\ xlo \le x \le xup \]

where A and C are arbitrary matrices and the rest are vectors

Not all these constraints have to be defined . Our example will only use \( xlo \), \( A \) and \( b \) Still, this could be handled by a general non-linear minimizer like Minuit by introducing so-called "slack" variables . However, quadp is tailored to objective functions not more complex than being quadratic . This allows usage of solving techniques which are even stable for problems involving for instance 500 variables, 100 inequality conditions and 50 equality conditions .

Enough said about quadratic programming, let's return to our example . Suppose, after a long day of doing physics, you have a look at your investments and realize that an early retirement is not possible, given the returns of your stocks . So what now ? ROOT to the rescue ...

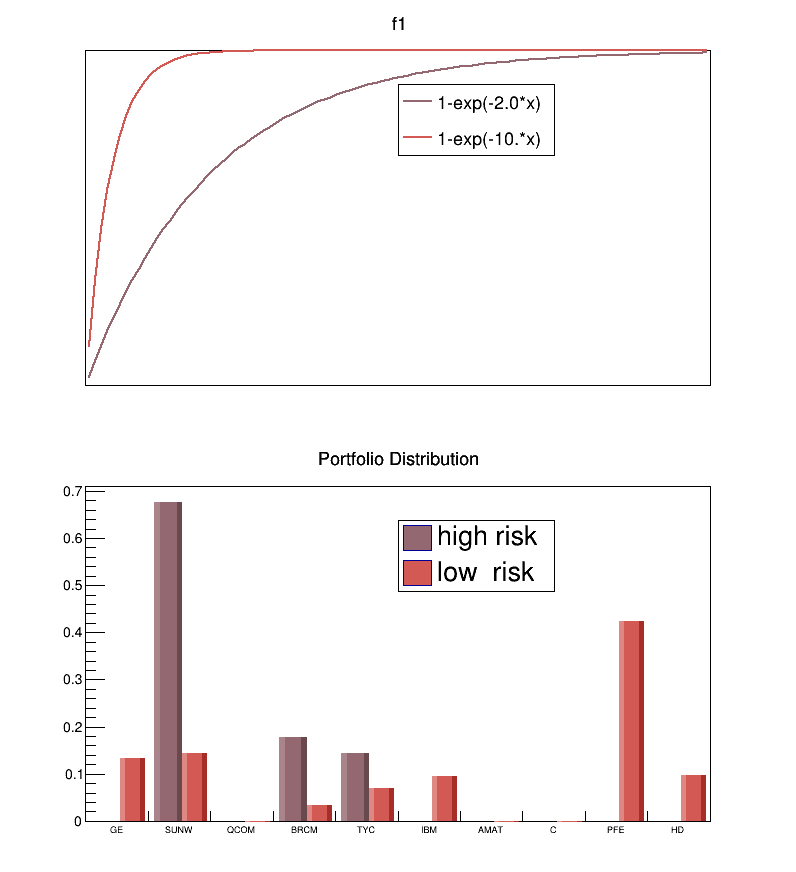
In 1990 Harry Markowitz was awarded the Nobel prize for economics: " his work provided new tools for weighing the risks and rewards of different investments and for valuing corporate stocks and bonds" . In plain English, he developed the tools to balance greed and fear, we want the maximum return with the minimum amount of risk. Our stock portfolio should be at the "Efficient Frontier". To quantify better the risk we are willing to take, we define a utility function \( U(x) \). It describes as a function of our total assets \( x \), our "satisfaction" . A common choice is \( 1-exp(-k*x) \) (the reason for the exponent will be clear later) . The parameter \( k \) is the risk-aversion factor . For small values of \( k \) the satisfaction is small for small values of \( x \); by increasing \( x \) the satisfaction can still be increased significantly . For large values of \( k \), \( U(x) \) increases rapidly to 1, there is no increase in satisfaction for additional dollars earned .

In summary :

Suppose we have for nrStocks the historical daily returns \( r = closing_price(n) - closing_price(n-1) \). Define a vector \( x \) of length of \( nrStocks \), which contains the fraction of our money invested in each stock . We can calculate the average daily return \( z \) of our portfolio and its variance using the portfolio covariance Covar :

\( z = r^T x \) and \( var = x^T Covar x \)

Assuming that the daily returns have a Normal distribution, \( N(x) \), so will \( z \) with mean \( r^T x \) and variance \( x^T Covar x \)

The expected value of the utility function is :

\[ E(u(x)) = Int (1-exp(-k*x) N(x) dx \\ = 1-exp(-k (r^T x - 0.5 k x^T Covar x) ) \\ \]

Its value is maximised by maximising \( r^T x -0.5 k x^T Covar x \) under the condition \( sum (x_i) = 1 \), meaning we want all our money invested and \( x_i \ge 0 \), we can not "short" a stock

For 10 stocks we got the historical daily data for Sep-2000 to Jun-2004:

We calculate the optimal portfolio for 2.0 and 10.0 .

Food for thought :

pict1_portfolio.C.png
Processing /mnt/build/workspace/root-makedoc-v608/rootspi/rdoc/src/v6-08-00-patches/tutorials/quadp/portfolio.C...
accessing stock.root file from http://root.cern.ch/files
stock daily daily w1 w2
symb return sdv
GE : 1.001 0.022 0.000 0.134
SUNW : 1.004 0.047 0.676 0.145
QCOM : 1.001 0.039 0.000 0.000
BRCM : 1.003 0.056 0.179 0.035
TYC : 1.001 0.042 0.145 0.069
IBM : 1.001 0.023 0.000 0.096
AMAT : 1.001 0.040 0.000 0.000
C : 1.000 0.023 0.000 0.000
PFE : 1.000 0.019 0.000 0.424
HD : 1.001 0.029 0.000 0.098
#include "Riostream.h"
#include "TCanvas.h"
#include "TFile.h"
#include "TMath.h"
#include "TTree.h"
#include "TArrayF.h"
#include "TH1.h"
#include "TF1.h"
#include "TLegend.h"
#include "TSystem.h"
#include "TMatrixD.h"
#include "TMatrixDSym.h"
#include "TVectorD.h"
#include "TQpProbDens.h"
#include "TGondzioSolver.h"
const Int_t nrStocks = 10;
static const Char_t *stocks[] =
{"GE","SUNW","QCOM","BRCM","TYC","IBM","AMAT","C","PFE","HD"};
class TStockDaily {
public:
Int_t fDate;
Int_t fOpen; // 100*open_price
Int_t fHigh; // 100*high_price
Int_t fLow; // 100*low_price
Int_t fClose; // 100*close_price
Int_t fVol;
Int_t fCloseAdj; // 100*close_price adjusted for splits and dividend
TStockDaily() {
fDate = fVol = fOpen = fHigh = fLow = fClose = fCloseAdj = 0;
}
virtual ~TStockDaily() {}
ClassDef(TStockDaily,1)
};
//---------------------------------------------------------------------------
Double_t RiskProfile(Double_t *x, Double_t *par) {
Double_t riskFactor = par[0];
return 1-TMath::Exp(-riskFactor*x[0]);
}
//---------------------------------------------------------------------------
TArrayF &StockReturn(TFile *f,const TString &name,Int_t sDay,Int_t eDay)
{
TTree *tDaily = (TTree*)f->Get(name);
TStockDaily *data = 0;
tDaily->SetBranchAddress("daily",&data);
TBranch *b_closeAdj = tDaily->GetBranch("fCloseAdj");
TBranch *b_date = tDaily->GetBranch("fDate");
//read only the "adjusted close" branch for all entries
const Int_t nrEntries = (Int_t)tDaily->GetEntries();
TArrayF closeAdj(nrEntries);
for (Int_t i = 0; i < nrEntries; i++) {
b_date->GetEntry(i);
b_closeAdj->GetEntry(i);
if (data->fDate >= sDay && data->fDate <= eDay)
closeAdj[i] = data->fCloseAdj/100.;
}
TArrayF *r = new TArrayF(nrEntries-1);
for (Int_t i = 1; i < nrEntries; i++)
// (*r)[i-1] = closeAdj[i]-closeAdj[i-1];
(*r)[i-1] = closeAdj[i]/closeAdj[i-1];
return *r;
}
#ifndef __MAKECINT__
//---------------------------------------------------------------------------
TVectorD OptimalInvest(Double_t riskFactor,TVectorD r,TMatrixDSym Covar)
{
// what the quadratic programming package will do:
//
// minimize c^T x + ( 1/2 ) x^T Q x
// subject to A x = b
// clo <= C x <= cup
// xlo <= x <= xup
// what we want :
//
// maximize c^T x - k ( 1/2 ) x^T Q x
// subject to sum_x x_i = 1
// 0 <= x_i
// We have nrStocks weights to determine,
// 1 equality- and 0 inequality- equations (the simple square boundary
// condition (xlo <= x <= xup) does not count)
const Int_t nrVar = nrStocks;
const Int_t nrEqual = 1;
const Int_t nrInEqual = 0;
// flip the sign of the objective function because we want to maximize
TVectorD c = -1.*r;
TMatrixDSym Q = riskFactor*Covar;
// equality equation
TMatrixD A(nrEqual,nrVar); A = 1;
TVectorD b(nrEqual); b = 1;
// inequality equation
//
// - although not applicable in the current situation since nrInEqual = 0, one
// has to specify not only clo and cup but also an index vector iclo and icup,
// whose values are either 0 or 1 . If iclo[j] = 1, the lower boundary condition
// is active on x[j], etc. ...
TMatrixD C (nrInEqual,nrVar);
TVectorD clo (nrInEqual);
TVectorD cup (nrInEqual);
TVectorD iclo(nrInEqual);
TVectorD icup(nrInEqual);
// simple square boundary condition : 0 <= x_i, so only xlo is relevant .
// Like for clo and cup above, we have to define an index vector ixlo and ixup .
// Since each variable has the lower boundary, we can set the whole vector
// ixlo = 1
TVectorD xlo (nrVar); xlo = 0;
TVectorD xup (nrVar); xup = 0;
TVectorD ixlo(nrVar); ixlo = 1;
TVectorD ixup(nrVar); ixup = 0;
// setup the quadratic programming problem . Since a small number of variables are
// involved and "Q" has everywhere entries, we chose the dense version "TQpProbDens" .
// In case of a sparse formulation, simply replace all "Dens" by "Sparse" below and
// use TMatrixDSparse instead of TMatrixDSym and TMatrixD
TQpProbDens *qp = new TQpProbDens(nrVar,nrEqual,nrInEqual);
// stuff all the matrices/vectors defined above in the proper places
TQpDataDens *prob = (TQpDataDens *)qp->MakeData(c,Q,xlo,ixlo,xup,ixup,A,b,C,clo,iclo,cup,icup);
// setup the nrStock variables, vars->fX will contain the final solution
TQpVar *vars = qp->MakeVariables(prob);
TQpResidual *resid = qp->MakeResiduals(prob);
// Now we have to choose the method of solving, either TGondzioSolver or TMehrotraSolver
// The Gondzio method is more sophisticated and therefore numerically more involved
// If one want the Mehrotra method, simply replace "Gondzio" by "Mehrotra" .
TGondzioSolver *s = new TGondzioSolver(qp,prob);
const Int_t status = s->Solve(prob,vars,resid);
const TVectorD weight = vars->fX;
delete qp; delete prob; delete vars; delete resid; delete s;
if (status != 0) {
cout << "Could not solve this problem." <<endl;
return TVectorD(nrStocks);
}
return weight;
}
#endif
//---------------------------------------------------------------------------
void portfolio()
{
const Int_t sDay = 20000809;
const Int_t eDay = 20040602;
const char *fname = "stock.root";
TFile *f = 0;
if (!gSystem->AccessPathName(fname)) {
f = TFile::Open(fname);
} else {
printf("accessing %s file from http://root.cern.ch/files\n",fname);
f = TFile::Open(Form("http://root.cern.ch/files/%s",fname));
}
if (!f) return;
TArrayF *data = new TArrayF[nrStocks];
for (Int_t i = 0; i < nrStocks; i++) {
const TString symbol = stocks[i];
data[i] = StockReturn(f,symbol,sDay,eDay);
}
const Int_t nrData = data[0].GetSize();
TVectorD r(nrStocks);
for (Int_t i = 0; i < nrStocks; i++)
r[i] = data[i].GetSum()/nrData;
TMatrixDSym Covar(nrStocks);
for (Int_t i = 0; i < nrStocks; i++) {
for (Int_t j = 0; j <= i; j++) {
Double_t sum = 0.;
for (Int_t k = 0; k < nrData; k++)
sum += (data[i][k]-r[i])*(data[j][k]-r[j]);
Covar(i,j) = Covar(j,i) = sum/nrData;
}
}
const TVectorD weight1 = OptimalInvest(2.0,r,Covar);
const TVectorD weight2 = OptimalInvest(10.,r,Covar);
cout << "stock daily daily w1 w2" <<endl;
cout << "symb return sdv " <<endl;
for (Int_t i = 0; i < nrStocks; i++)
printf("%s\t: %.3f %.3f %.3f %.3f\n",stocks[i],r[i],TMath::Sqrt(Covar[i][i]),weight1[i],weight2[i]);
TCanvas *c1 = new TCanvas("c1","Portfolio Optimizations",10,10,800,900);
c1->Divide(1,2);
// utility function / risk profile
c1->cd(1);
gPad->SetGridx();
gPad->SetGridy();
TF1 *f1 = new TF1("f1",RiskProfile,0,2.5,1);
f1->SetParameter(0,2.0);
f1->SetLineColor(49);
f1->Draw("AC");
f1->GetHistogram()->SetXTitle("dollar");
f1->GetHistogram()->SetYTitle("utility");
f1->GetHistogram()->SetMinimum(0.0);
f1->GetHistogram()->SetMaximum(1.0);
TF1 *f2 = new TF1("f2",RiskProfile,0,2.5,1);
f2->SetParameter(0,10.);
f2->SetLineColor(50);
f2->Draw("CSAME");
TLegend *legend1 = new TLegend(0.50,0.65,0.70,0.82);
legend1->AddEntry(f1,"1-exp(-2.0*x)","l");
legend1->AddEntry(f2,"1-exp(-10.*x)","l");
legend1->Draw();
// vertical bar chart of portfolio distribution
c1->cd(2);
TH1F *h1 = new TH1F("h1","Portfolio Distribution",nrStocks,0,0);
TH1F *h2 = new TH1F("h2","Portfolio Distribution",nrStocks,0,0);
h1->SetStats(0);
h1->SetFillColor(49);
h2->SetFillColor(50);
h1->SetBarWidth(0.45);
h1->SetBarOffset(0.1);
h2->SetBarWidth(0.4);
h2->SetBarOffset(0.55);
for (Int_t i = 0; i < nrStocks; i++) {
h1->Fill(stocks[i],weight1[i]);
h2->Fill(stocks[i],weight2[i]);
}
h1->Draw("BAR2 HIST");
h2->Draw("BAR2SAME HIST");
TLegend *legend2 = new TLegend(0.50,0.65,0.70,0.82);
legend2->AddEntry(h1,"high risk","f");
legend2->AddEntry(h2,"low risk","f");
legend2->Draw();
}
Author
Eddy Offermann

Definition in file portfolio.C.