
 Example of CrystalBall Function and its distribution (pdf and cdf)
Example of CrystalBall Function and its distribution (pdf and cdf)
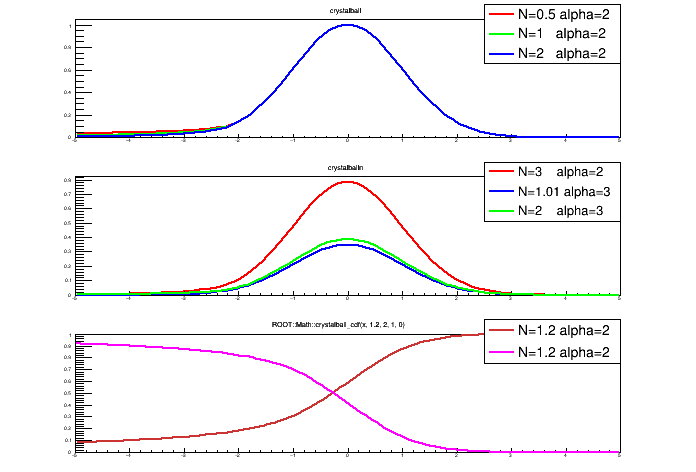
void CrystalBall() {
auto f1 =
new TF1(
"f1",
"crystalball",-5,5);
f1->SetParameters(1, 0, 1, 2, 0.5);
f1->SetLineColor(kRed);
auto f2 =
new TF1(
"f2",
"ROOT::Math::crystalball_function(x, 2, 1, 1, 0)",-5,5);
auto f3 =
new TF1(
"f3",
"ROOT::Math::crystalball_function(x, 2, 2, 1, 0)",-5,5);
auto legend =
new TLegend(0.7,0.6,0.9,1.);
legend->
AddEntry(f1,
"N=0.5 alpha=2",
"L");
auto pdf1 =
new TF1(
"pdf",
"crystalballn",-5,5);
pdf1->SetParameters(2, 0, 1, 2, 3);
pdf1->Draw();
auto pdf2 =
new TF1(
"pdf",
"ROOT::Math::crystalball_pdf(x, 3, 1.01, 1, 0)",-5,5);
pdf2->SetLineColor(kBlue);
pdf2->Draw("same");
auto pdf3 =
new TF1(
"pdf",
"ROOT::Math::crystalball_pdf(x, 2, 2, 1, 0)",-5,5);
pdf3->Draw("same");
legend =
new TLegend(0.7,0.6,0.9,1.);
legend->
AddEntry(pdf1,
"N=3 alpha=2",
"L");
legend->
AddEntry(pdf2,
"N=1.01 alpha=3",
"L");
legend->
AddEntry(pdf3,
"N=2 alpha=3",
"L");
auto cdf =
new TF1(
"cdf",
"ROOT::Math::crystalball_cdf(x, 1.2, 2, 1, 0)",-5,5);
auto cdfc =
new TF1(
"cdfc",
"ROOT::Math::crystalball_cdf_c(x, 1.2, 2, 1, 0)",-5,5);
cdf->SetLineColor(kRed-3);
cdfc->Draw("Same");
legend =
new TLegend(0.7,0.7,0.9,1.);
legend->
AddEntry(cdfc,
"N=1.2 alpha=2",
"L");
}
- Author
- Lorenzo Moneta
Definition in file CrystalBall.C.



 Example of CrystalBall Function and its distribution (pdf and cdf)
Example of CrystalBall Function and its distribution (pdf and cdf) 