Example macro describing how to use the special mathematical functions taking full advantage of the precision and speed of the C99 compliant environments.
Example macro describing how to use the special mathematical functions taking full advantage of the precision and speed of the C99 compliant environments.
To execute the macro type in:
root[0] .x mathcoreSpecFunc.C
It will create two canvases:
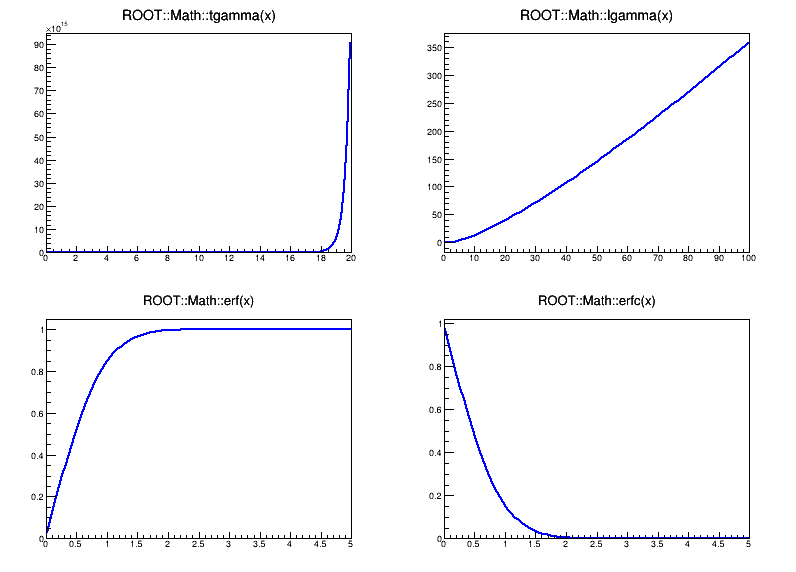
- one with the representation of the tgamma, lgamma, erf and erfc functions
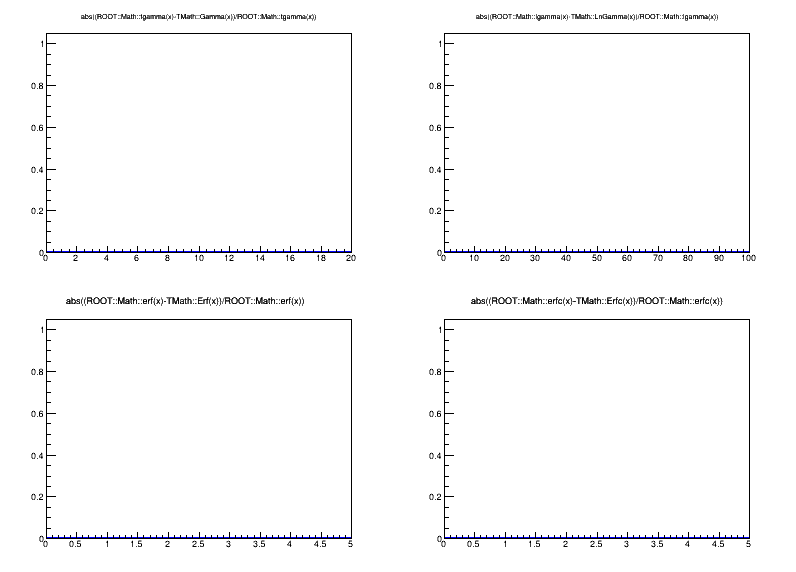
- one with the relative difference between the old ROOT versions and the C99 implementation (on obsolete platform+compiler combinations which are not C99 compliant it will call the original ROOT implementations, hence the difference will be 0)
The naming and numbering of the functions is taken from [Matt Austern, (Draft) Technical Report on Standard Library Extensions, N1687=04-0127, September 10, 2004](A HREF="http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2004/n1687.pdf")
void mathcoreSpecFunc() {
TF1 *f1a =
new TF1(
"f1a",
"ROOT::Math::tgamma(x)",0,20);
TF1 *f1b =
new TF1(
"f1b",
"abs((ROOT::Math::tgamma(x)-TMath::Gamma(x))/ROOT::Math::tgamma(x))",0,20);
TF1 *f2a =
new TF1(
"f2a",
"ROOT::Math::lgamma(x)",0,100);
TF1 *f2b =
new TF1(
"f2b",
"abs((ROOT::Math::lgamma(x)-TMath::LnGamma(x))/ROOT::Math::lgamma(x))",0,100);
TF1 *f3a =
new TF1(
"f3a",
"ROOT::Math::erf(x)",0,5);
TF1 *f3b =
new TF1(
"f3b",
"abs((ROOT::Math::erf(x)-TMath::Erf(x))/ROOT::Math::erf(x))",0,5);
TF1 *f4a =
new TF1(
"f4a",
"ROOT::Math::erfc(x)",0,5);
TF1 *f4b =
new TF1(
"f4b",
"abs((ROOT::Math::erfc(x)-TMath::Erfc(x))/ROOT::Math::erfc(x))",0,5);
}
- Author
- Andras Zsenei
Definition in file mathcoreSpecFunc.C.



 Example macro describing how to use the special mathematical functions taking full advantage of the precision and speed of the C99 compliant environments.
Example macro describing how to use the special mathematical functions taking full advantage of the precision and speed of the C99 compliant environments.