 |
ROOT 6.12/07 Reference Guide |
 |
ROOT 6.12/07 Reference Guide |
Classes | |
| struct | Limits |
Functions | |
| Short_t | Abs (Short_t d) |
| Int_t | Abs (Int_t d) |
| Long_t | Abs (Long_t d) |
| Long64_t | Abs (Long64_t d) |
| Float_t | Abs (Float_t d) |
| Double_t | Abs (Double_t d) |
| LongDouble_t | Abs (LongDouble_t d) |
| Double_t | ACos (Double_t) |
| Double_t | ACosH (Double_t) |
| Bool_t | AreEqualAbs (Double_t af, Double_t bf, Double_t epsilon) |
| Bool_t | AreEqualRel (Double_t af, Double_t bf, Double_t relPrec) |
| Double_t | ASin (Double_t) |
| Double_t | ASinH (Double_t) |
| Double_t | ATan (Double_t) |
| Double_t | ATan2 (Double_t, Double_t) |
| Double_t | ATanH (Double_t) |
| Double_t | BesselI (Int_t n, Double_t x) |
| Compute the Integer Order Modified Bessel function I_n(x) for n=0,1,2,... More... | |
| Double_t | BesselI0 (Double_t x) |
| Compute the modified Bessel function I_0(x) for any real x. More... | |
| Double_t | BesselI1 (Double_t x) |
| Compute the modified Bessel function I_1(x) for any real x. More... | |
| Double_t | BesselJ0 (Double_t x) |
| Returns the Bessel function J0(x) for any real x. More... | |
| Double_t | BesselJ1 (Double_t x) |
| Returns the Bessel function J1(x) for any real x. More... | |
| Double_t | BesselK (Int_t n, Double_t x) |
| Compute the Integer Order Modified Bessel function K_n(x) for n=0,1,2,... More... | |
| Double_t | BesselK0 (Double_t x) |
| Compute the modified Bessel function K_0(x) for positive real x. More... | |
| Double_t | BesselK1 (Double_t x) |
| Compute the modified Bessel function K_1(x) for positive real x. More... | |
| Double_t | BesselY0 (Double_t x) |
| Returns the Bessel function Y0(x) for positive x. More... | |
| Double_t | BesselY1 (Double_t x) |
| Returns the Bessel function Y1(x) for positive x. More... | |
| Double_t | Beta (Double_t p, Double_t q) |
| Calculates Beta-function Gamma(p)*Gamma(q)/Gamma(p+q). More... | |
| Double_t | BetaCf (Double_t x, Double_t a, Double_t b) |
| Continued fraction evaluation by modified Lentz's method used in calculation of incomplete Beta function. More... | |
| Double_t | BetaDist (Double_t x, Double_t p, Double_t q) |
| Computes the probability density function of the Beta distribution (the distribution function is computed in BetaDistI). More... | |
| Double_t | BetaDistI (Double_t x, Double_t p, Double_t q) |
| Computes the distribution function of the Beta distribution. More... | |
| Double_t | BetaIncomplete (Double_t x, Double_t a, Double_t b) |
| Calculates the incomplete Beta-function. More... | |
| template<typename T > | |
| Long64_t | BinarySearch (Long64_t n, const T *array, T value) |
| template<typename T > | |
| Long64_t | BinarySearch (Long64_t n, const T **array, T value) |
| template<typename Iterator , typename Element > | |
| Iterator | BinarySearch (Iterator first, Iterator last, Element value) |
| Double_t | Binomial (Int_t n, Int_t k) |
| Calculate the binomial coefficient n over k. More... | |
| Double_t | BinomialI (Double_t p, Int_t n, Int_t k) |
| Suppose an event occurs with probability p per trial Then the probability P of its occurring k or more times in n trials is termed a cumulative binomial probability the formula is P = sum_from_j=k_to_n(TMath::Binomial(n, j)* *TMath::Power(p, j)*TMathPower(1-p, n-j) For n larger than 12 BetaIncomplete is a much better way to evaluate the sum than would be the straightforward sum calculation for n smaller than 12 either method is acceptable ("Numerical Recipes") –implementation by Anna Kreshuk. More... | |
| Double_t | BreitWigner (Double_t x, Double_t mean=0, Double_t gamma=1) |
| Calculate a Breit Wigner function with mean and gamma. More... | |
| void | BubbleHigh (Int_t Narr, Double_t *arr1, Int_t *arr2) |
| Bubble sort variant to obtain the order of an array's elements into an index in order to do more useful things than the standard built in functions. More... | |
| void | BubbleLow (Int_t Narr, Double_t *arr1, Int_t *arr2) |
| Opposite ordering of the array arr2[] to that of BubbleHigh. More... | |
| constexpr Double_t | C () |
| Double_t | CauchyDist (Double_t x, Double_t t=0, Double_t s=1) |
| Computes the density of Cauchy distribution at point x by default, standard Cauchy distribution is used (t=0, s=1) t is the location parameter s is the scale parameter The Cauchy distribution, also called Lorentzian distribution, is a continuous distribution describing resonance behavior The mean and standard deviation of the Cauchy distribution are undefined. More... | |
| constexpr Double_t | Ccgs () |
| Double_t | Ceil (Double_t x) |
| Int_t | CeilNint (Double_t x) |
| Double_t | ChisquareQuantile (Double_t p, Double_t ndf) |
| Evaluate the quantiles of the chi-squared probability distribution function. More... | |
| Double_t | Cos (Double_t) |
| Double_t | CosH (Double_t) |
| template<typename T > | |
| T * | Cross (const T v1[3], const T v2[3], T out[3]) |
| constexpr Double_t | CUncertainty () |
| constexpr Double_t | DegToRad () |
| Double_t | DiLog (Double_t x) |
| The DiLogarithm function Code translated by R.Brun from CERNLIB DILOG function C332. More... | |
| constexpr Double_t | E () |
| Double_t | Erf (Double_t x) |
| Computation of the error function erf(x). More... | |
| Double_t | Erfc (Double_t x) |
| Compute the complementary error function erfc(x). More... | |
| Double_t | ErfcInverse (Double_t x) |
| Double_t | ErfInverse (Double_t x) |
| returns the inverse error function x must be <-1<x<1 More... | |
| constexpr Double_t | EulerGamma () |
| Bool_t | Even (Long_t a) |
| Double_t | Exp (Double_t x) |
| Double_t | Factorial (Int_t i) |
| Compute factorial(n). More... | |
| Double_t | FDist (Double_t F, Double_t N, Double_t M) |
| Computes the density function of F-distribution (probability function, integral of density, is computed in FDistI). More... | |
| Double_t | FDistI (Double_t F, Double_t N, Double_t M) |
| Calculates the cumulative distribution function of F-distribution, this function occurs in the statistical test of whether two observed samples have the same variance. More... | |
| Int_t | Finite (Double_t x) |
| Int_t | Finite (Float_t x) |
| Double_t | Floor (Double_t x) |
| Int_t | FloorNint (Double_t x) |
| Double_t | Freq (Double_t x) |
| Computation of the normal frequency function freq(x). More... | |
| constexpr Double_t | G () |
| Double_t | GamCf (Double_t a, Double_t x) |
| Computation of the incomplete gamma function P(a,x) via its continued fraction representation. More... | |
| Double_t | Gamma (Double_t z) |
| Computation of gamma(z) for all z. More... | |
| Double_t | Gamma (Double_t a, Double_t x) |
| Computation of the normalized lower incomplete gamma function P(a,x) as defined in the Handbook of Mathematical Functions by Abramowitz and Stegun, formula 6.5.1 on page 260 . More... | |
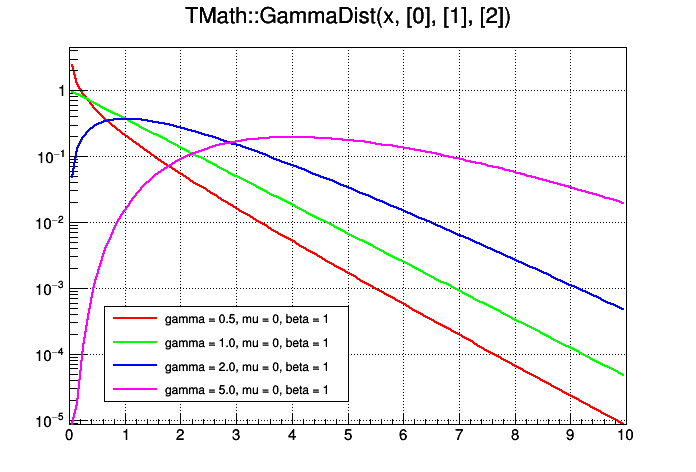
| Double_t | GammaDist (Double_t x, Double_t gamma, Double_t mu=0, Double_t beta=1) |
| Computes the density function of Gamma distribution at point x. More... | |
| Double_t | GamSer (Double_t a, Double_t x) |
| Computation of the incomplete gamma function P(a,x) via its series representation. More... | |
| Double_t | Gaus (Double_t x, Double_t mean=0, Double_t sigma=1, Bool_t norm=kFALSE) |
| Calculate a gaussian function with mean and sigma. More... | |
| constexpr Double_t | Gcgs () |
| template<typename T > | |
| Double_t | GeomMean (Long64_t n, const T *a) |
| template<typename Iterator > | |
| Double_t | GeomMean (Iterator first, Iterator last) |
| constexpr Double_t | GhbarC () |
| constexpr Double_t | GhbarCUncertainty () |
| constexpr Double_t | Gn () |
| constexpr Double_t | GnUncertainty () |
| constexpr Double_t | GUncertainty () |
| constexpr Double_t | H () |
| ULong_t | Hash (const void *txt, Int_t ntxt) |
| Calculates hash index from any char string. More... | |
| ULong_t | Hash (const char *str) |
| Return a case-sensitive hash value (endian independent). More... | |
| constexpr Double_t | Hbar () |
| constexpr Double_t | Hbarcgs () |
| constexpr Double_t | HbarUncertainty () |
| constexpr Double_t | HC () |
| constexpr Double_t | HCcgs () |
| constexpr Double_t | Hcgs () |
| constexpr Double_t | HUncertainty () |
| Double_t | Hypot (Double_t x, Double_t y) |
| Long_t | Hypot (Long_t x, Long_t y) |
| Double_t | Infinity () |
| constexpr Double_t | InvPi () |
| template<typename T > | |
| Bool_t | IsInside (T xp, T yp, Int_t np, T *x, T *y) |
| Bool_t | IsNaN (Double_t x) |
| Bool_t | IsNaN (Float_t x) |
| constexpr Double_t | K () |
| constexpr Double_t | Kcgs () |
| Double_t | KolmogorovProb (Double_t z) |
| Calculates the Kolmogorov distribution function,. More... | |
| Double_t | KolmogorovTest (Int_t na, const Double_t *a, Int_t nb, const Double_t *b, Option_t *option) |
| Statistical test whether two one-dimensional sets of points are compatible with coming from the same parent distribution, using the Kolmogorov test. More... | |
| template<class Element , typename Size > | |
| Element | KOrdStat (Size n, const Element *a, Size k, Size *work=0) |
| constexpr Double_t | KUncertainty () |
| Double_t | Landau (Double_t x, Double_t mpv=0, Double_t sigma=1, Bool_t norm=kFALSE) |
| The LANDAU function. More... | |
| Double_t | LandauI (Double_t x) |
| Returns the value of the Landau distribution function at point x. More... | |
| Double_t | LaplaceDist (Double_t x, Double_t alpha=0, Double_t beta=1) |
| Computes the probability density function of Laplace distribution at point x, with location parameter alpha and shape parameter beta. More... | |
| Double_t | LaplaceDistI (Double_t x, Double_t alpha=0, Double_t beta=1) |
| Computes the distribution function of Laplace distribution at point x, with location parameter alpha and shape parameter beta. More... | |
| Double_t | Ldexp (Double_t x, Int_t exp) |
| constexpr Double_t | Ln10 () |
| Double_t | LnGamma (Double_t z) |
| Computation of ln[gamma(z)] for all z. More... | |
| template<typename T > | |
| Long64_t | LocMax (Long64_t n, const T *a) |
| template<typename Iterator > | |
| Iterator | LocMax (Iterator first, Iterator last) |
| template<typename T > | |
| Long64_t | LocMin (Long64_t n, const T *a) |
| template<typename Iterator > | |
| Iterator | LocMin (Iterator first, Iterator last) |
| Double_t | Log (Double_t x) |
| Double_t | Log10 (Double_t x) |
| Double_t | Log2 (Double_t x) |
| constexpr Double_t | LogE () |
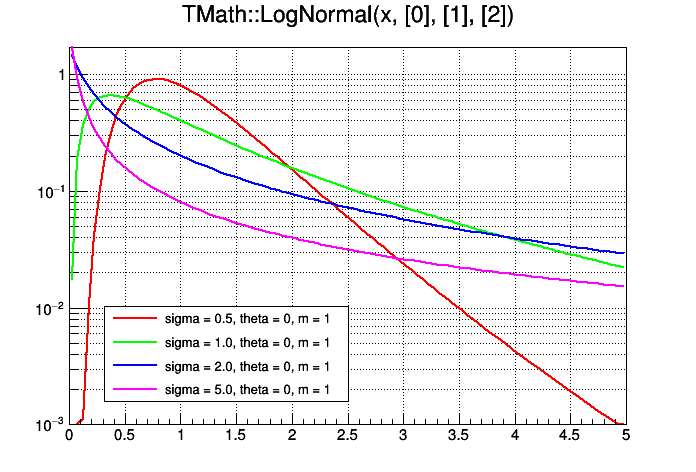
| Double_t | LogNormal (Double_t x, Double_t sigma, Double_t theta=0, Double_t m=1) |
| Computes the density of LogNormal distribution at point x. More... | |
| Short_t | Max (Short_t a, Short_t b) |
| UShort_t | Max (UShort_t a, UShort_t b) |
| Int_t | Max (Int_t a, Int_t b) |
| UInt_t | Max (UInt_t a, UInt_t b) |
| Long_t | Max (Long_t a, Long_t b) |
| ULong_t | Max (ULong_t a, ULong_t b) |
| Long64_t | Max (Long64_t a, Long64_t b) |
| ULong64_t | Max (ULong64_t a, ULong64_t b) |
| Float_t | Max (Float_t a, Float_t b) |
| Double_t | Max (Double_t a, Double_t b) |
| template<typename T > | |
| T | MaxElement (Long64_t n, const T *a) |
| template<typename T > | |
| Double_t | Mean (Long64_t n, const T *a, const Double_t *w=0) |
| template<typename Iterator > | |
| Double_t | Mean (Iterator first, Iterator last) |
| template<typename Iterator , typename WeightIterator > | |
| Double_t | Mean (Iterator first, Iterator last, WeightIterator wfirst) |
| template<typename T > | |
| Double_t | Median (Long64_t n, const T *a, const Double_t *w=0, Long64_t *work=0) |
| Short_t | Min (Short_t a, Short_t b) |
| UShort_t | Min (UShort_t a, UShort_t b) |
| Int_t | Min (Int_t a, Int_t b) |
| UInt_t | Min (UInt_t a, UInt_t b) |
| Long_t | Min (Long_t a, Long_t b) |
| ULong_t | Min (ULong_t a, ULong_t b) |
| Long64_t | Min (Long64_t a, Long64_t b) |
| ULong64_t | Min (ULong64_t a, ULong64_t b) |
| Float_t | Min (Float_t a, Float_t b) |
| Double_t | Min (Double_t a, Double_t b) |
| template<typename T > | |
| T | MinElement (Long64_t n, const T *a) |
| constexpr Double_t | MWair () |
| constexpr Double_t | Na () |
| constexpr Double_t | NaUncertainty () |
| Long_t | NextPrime (Long_t x) |
| TMath Base functionsDefine the functions Min, Max, Abs, Sign, Range for all types. More... | |
| template<typename T > | |
| Int_t | Nint (T x) |
| template<typename T > | |
| T * | Normal2Plane (const T v1[3], const T v2[3], const T v3[3], T normal[3]) |
| Float_t | Normalize (Float_t v[3]) |
| Normalize a vector v in place. More... | |
| Double_t | Normalize (Double_t v[3]) |
| Normalize a vector v in place. More... | |
| template<typename T > | |
| T | NormCross (const T v1[3], const T v2[3], T out[3]) |
| Double_t | NormQuantile (Double_t p) |
| Computes quantiles for standard normal distribution N(0, 1) at probability p ALGORITHM AS241 APPL. More... | |
| Bool_t | Odd (Long_t a) |
| Bool_t | Permute (Int_t n, Int_t *a) |
| Simple recursive algorithm to find the permutations of n natural numbers, not necessarily all distinct adapted from CERNLIB routine PERMU. More... | |
| constexpr Double_t | Pi () |
| constexpr Double_t | PiOver2 () |
| constexpr Double_t | PiOver4 () |
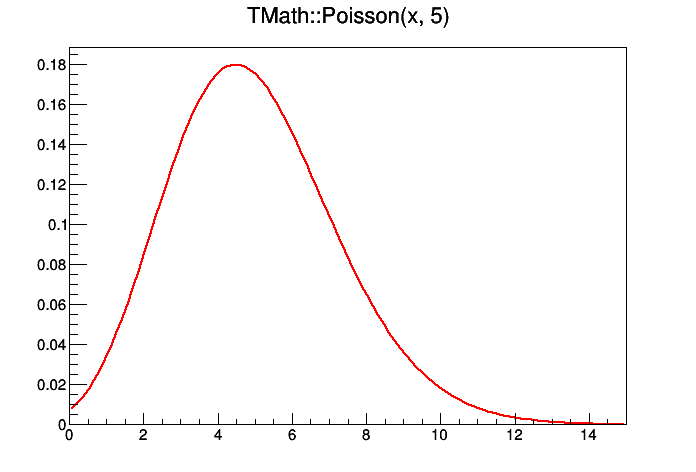
| Double_t | Poisson (Double_t x, Double_t par) |
| Compute the Poisson distribution function for (x,par) The Poisson PDF is implemented by means of Euler's Gamma-function (for the factorial), so for any x integer argument it is correct. More... | |
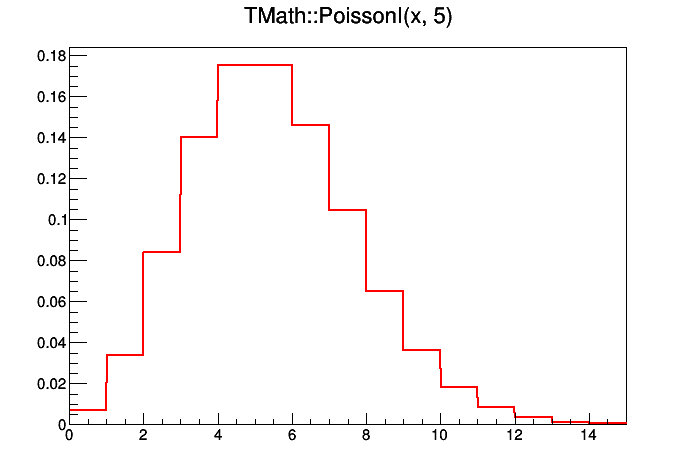
| Double_t | PoissonI (Double_t x, Double_t par) |
| compute the Poisson distribution function for (x,par) This is a non-smooth function. More... | |
| LongDouble_t | Power (LongDouble_t x, LongDouble_t y) |
| LongDouble_t | Power (LongDouble_t x, Long64_t y) |
| LongDouble_t | Power (Long64_t x, Long64_t y) |
| Double_t | Power (Double_t x, Double_t y) |
| Double_t | Power (Double_t x, Int_t y) |
| Double_t | Prob (Double_t chi2, Int_t ndf) |
| Computation of the probability for a certain Chi-squared (chi2) and number of degrees of freedom (ndf). More... | |
| constexpr Double_t | Qe () |
| constexpr Double_t | QeUncertainty () |
| void | Quantiles (Int_t n, Int_t nprob, Double_t *x, Double_t *quantiles, Double_t *prob, Bool_t isSorted=kTRUE, Int_t *index=0, Int_t type=7) |
| Computes sample quantiles, corresponding to the given probabilities Parameters: x -the data sample n - its size quantiles - computed quantiles are returned in there prob - probabilities where to compute quantiles nprob - size of prob array isSorted - is the input array x sorted? NOTE, that when the input is not sorted, an array of integers of size n needs to be allocated. More... | |
| Double_t | QuietNaN () |
| constexpr Double_t | R () |
| constexpr Double_t | RadToDeg () |
| Short_t | Range (Short_t lb, Short_t ub, Short_t x) |
| Int_t | Range (Int_t lb, Int_t ub, Int_t x) |
| Long_t | Range (Long_t lb, Long_t ub, Long_t x) |
| ULong_t | Range (ULong_t lb, ULong_t ub, ULong_t x) |
| Double_t | Range (Double_t lb, Double_t ub, Double_t x) |
| constexpr Double_t | Rgair () |
| template<typename T > | |
| Double_t | RMS (Long64_t n, const T *a, const Double_t *w=0) |
| template<typename Iterator > | |
| Double_t | RMS (Iterator first, Iterator last) |
| template<typename Iterator , typename WeightIterator > | |
| Double_t | RMS (Iterator first, Iterator last, WeightIterator wfirst) |
| Bool_t | RootsCubic (const Double_t coef[4], Double_t &a, Double_t &b, Double_t &c) |
| Calculates roots of polynomial of 3rd order a*x^3 + b*x^2 + c*x + d, where a == coef[3], b == coef[2], c == coef[1], d == coef[0] coef[3] must be different from 0 If the boolean returned by the method is false: ==> there are 3 real roots a,b,c If the boolean returned by the method is true: ==> there is one real root a and 2 complex conjugates roots (b+i*c,b-i*c) More... | |
| constexpr Double_t | RUncertainty () |
| constexpr Double_t | Sigma () |
| constexpr Double_t | SigmaUncertainty () |
| template<typename T1 , typename T2 > | |
| T1 | Sign (T1 a, T2 b) |
| Float_t | Sign (Float_t a, Float_t b) |
| Double_t | Sign (Double_t a, Double_t b) |
| LongDouble_t | Sign (LongDouble_t a, LongDouble_t b) |
| Double_t | SignalingNaN () |
| template<typename Integer > | |
| Bool_t | SignBit (Integer a) |
| Bool_t | SignBit (Float_t a) |
| Bool_t | SignBit (Double_t a) |
| Bool_t | SignBit (LongDouble_t a) |
| Double_t | Sin (Double_t) |
| Double_t | SinH (Double_t) |
| template<typename Element , typename Index > | |
| void | Sort (Index n, const Element *a, Index *index, Bool_t down=kTRUE) |
| template<typename Iterator , typename IndexIterator > | |
| void | SortItr (Iterator first, Iterator last, IndexIterator index, Bool_t down=kTRUE) |
| Double_t | Sq (Double_t x) |
| Double_t | Sqrt (Double_t x) |
| constexpr Double_t | Sqrt2 () |
| template<typename T > | |
| Double_t | StdDev (Long64_t n, const T *a, const Double_t *w=0) |
| template<typename Iterator > | |
| Double_t | StdDev (Iterator first, Iterator last) |
| template<typename Iterator , typename WeightIterator > | |
| Double_t | StdDev (Iterator first, Iterator last, WeightIterator wfirst) |
| Double_t | StruveH0 (Double_t x) |
| Struve Functions of Order 0. More... | |
| Double_t | StruveH1 (Double_t x) |
| Struve Functions of Order 1. More... | |
| Double_t | StruveL0 (Double_t x) |
| Modified Struve Function of Order 0. More... | |
| Double_t | StruveL1 (Double_t x) |
| Modified Struve Function of Order 1. More... | |
| Double_t | Student (Double_t T, Double_t ndf) |
| Computes density function for Student's t- distribution (the probability function (integral of density) is computed in StudentI). More... | |
| Double_t | StudentI (Double_t T, Double_t ndf) |
| Calculates the cumulative distribution function of Student's t-distribution second parameter stands for number of degrees of freedom, not for the number of samples if x has Student's t-distribution, the function returns the probability of x being less than T. More... | |
| Double_t | StudentQuantile (Double_t p, Double_t ndf, Bool_t lower_tail=kTRUE) |
| Computes quantiles of the Student's t-distribution 1st argument is the probability, at which the quantile is computed 2nd argument - the number of degrees of freedom of the Student distribution When the 3rd argument lower_tail is kTRUE (default)- the algorithm returns such x0, that P(x < x0)=p upper tail (lower_tail is kFALSE)- the algorithm returns such x0, that P(x > x0)=p the algorithm was taken from G.W.Hill, "Algorithm 396, Student's t-quantiles" "Communications of the ACM", 13(10), October 1970. More... | |
| Double_t | Tan (Double_t) |
| Double_t | TanH (Double_t) |
| constexpr Double_t | TwoPi () |
| Double_t | Vavilov (Double_t x, Double_t kappa, Double_t beta2) |
| Returns the value of the Vavilov density function Parameters: 1st - the point were the density function is evaluated 2nd - value of kappa (distribution parameter) 3rd - value of beta2 (distribution parameter) The algorithm was taken from the CernLib function vavden(G115) Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution Nucl.Instr. More... | |
| Double_t | VavilovDenEval (Double_t rlam, Double_t *AC, Double_t *HC, Int_t itype) |
| Internal function, called by Vavilov and VavilovSet. More... | |
| Double_t | VavilovI (Double_t x, Double_t kappa, Double_t beta2) |
| Returns the value of the Vavilov distribution function Parameters: 1st - the point were the density function is evaluated 2nd - value of kappa (distribution parameter) 3rd - value of beta2 (distribution parameter) The algorithm was taken from the CernLib function vavden(G115) Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution Nucl.Instr. More... | |
| void | VavilovSet (Double_t rkappa, Double_t beta2, Bool_t mode, Double_t *WCM, Double_t *AC, Double_t *HC, Int_t &itype, Int_t &npt) |
| Internal function, called by Vavilov and VavilovI. More... | |
| Double_t | Voigt (Double_t x, Double_t sigma, Double_t lg, Int_t r=4) |
| Computation of Voigt function (normalised). More... | |
Definition at line 108 of file TMathBase.h.
Definition at line 111 of file TMathBase.h.
Definition at line 114 of file TMathBase.h.
Definition at line 117 of file TMathBase.h.
Definition at line 124 of file TMathBase.h.
Definition at line 127 of file TMathBase.h.
|
inline |
Definition at line 130 of file TMathBase.h.
Computes the probability density function of the Beta distribution (the distribution function is computed in BetaDistI).
The first argument is the point, where the function will be computed, second and third are the function parameters. Since the Beta distribution is bounded on both sides, it's often used to represent processes with natural lower and upper limits.
Computes the distribution function of the Beta distribution.
The first argument is the point, where the function will be computed, second and third are the function parameters. Since the Beta distribution is bounded on both sides, it's often used to represent processes with natural lower and upper limits.
| Iterator TMath::BinarySearch | ( | Iterator | first, |
| Iterator | last, | ||
| Element | value | ||
| ) |
Suppose an event occurs with probability p per trial Then the probability P of its occurring k or more times in n trials is termed a cumulative binomial probability the formula is P = sum_from_j=k_to_n(TMath::Binomial(n, j)* *TMath::Power(p, j)*TMathPower(1-p, n-j) For n larger than 12 BetaIncomplete is a much better way to evaluate the sum than would be the straightforward sum calculation for n smaller than 12 either method is acceptable ("Numerical Recipes") –implementation by Anna Kreshuk.
Bubble sort variant to obtain the order of an array's elements into an index in order to do more useful things than the standard built in functions.
*arr1 is unchanged; *arr2 is the array of indicies corresponding to the descending value of arr1 with arr2[0] corresponding to the largest arr1 value and arr2[Narr] the smallest.
Computes the density of Cauchy distribution at point x by default, standard Cauchy distribution is used (t=0, s=1) t is the location parameter s is the scale parameter The Cauchy distribution, also called Lorentzian distribution, is a continuous distribution describing resonance behavior The mean and standard deviation of the Cauchy distribution are undefined.
The practical meaning of this is that collecting 1,000 data points gives no more accurate an estimate of the mean and standard deviation than does a single point. The formula was taken from "Engineering Statistics Handbook" on site http://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm Implementation by Anna Kreshuk. Example: TF1* fc = new TF1("fc", "TMath::CauchyDist(x, [0], [1])", -5, 5); fc->SetParameters(0, 1); fc->Draw();
Evaluate the quantiles of the chi-squared probability distribution function.
Algorithm AS 91 Appl. Statist. (1975) Vol.24, P.35 implemented by Anna Kreshuk. Incorporates the suggested changes in AS R85 (vol.40(1), pp.233-5, 1991) Parameters: p - the probability value, at which the quantile is computed ndf - number of degrees of freedom
| T * TMath::Cross | ( | const T | v1[3], |
| const T | v2[3], | ||
| T | out[3] | ||
| ) |
Definition at line 100 of file TMathBase.h.
Computes the density function of F-distribution (probability function, integral of density, is computed in FDistI).
Parameters N and M stand for degrees of freedom of chi-squares mentioned above parameter F is the actual variable x of the density function p(x) and the point at which the density function is calculated.
About F distribution: F-distribution arises in testing whether two random samples have the same variance. It is the ratio of two chi-square distributions, with N and M degrees of freedom respectively, where each chi-square is first divided by it's number of degrees of freedom. Implementation by Anna Kreshuk.
Calculates the cumulative distribution function of F-distribution, this function occurs in the statistical test of whether two observed samples have the same variance.
For this test a certain statistic F, the ratio of observed dispersion of the first sample to that of the second sample, is calculated. N and M stand for numbers of degrees of freedom in the samples 1-FDistI() is the significance level at which the hypothesis "1 has smaller variance than 2" can be rejected. A small numerical value of 1 - FDistI() implies a very significant rejection, in turn implying high confidence in the hypothesis "1 has variance greater than 2". Implementation by Anna Kreshuk.
Computation of the normalized lower incomplete gamma function P(a,x) as defined in the Handbook of Mathematical Functions by Abramowitz and Stegun, formula 6.5.1 on page 260 .
Its normalization is such that TMath::Gamma(a,+infinity) = 1 .
\[ P(a, x) = \frac{1}{\Gamma(a)} \int_{0}^{x} t^{a-1} e^{-t} dt \]
Computes the density function of Gamma distribution at point x.
gamma - shape parameter mu - location parameter beta - scale parameter
The definition can be found in "Engineering Statistics Handbook" on site http://www.itl.nist.gov/div898/handbook/eda/section3/eda366b.htm use now implementation in ROOT::Math::gamma_pdf
| Double_t TMath::GeomMean | ( | Iterator | first, |
| Iterator | last | ||
| ) |
Calculates hash index from any char string.
Based on pre-calculated table of 256 specially selected numbers. These numbers are selected in such a way, that for string length == 4 (integer number) the hash is unambiguous, i.e. from hash value we can recalculate input (no degeneration).
The quality of hash method is good enough, that "random" numbers made as R = Hash(1), Hash(2), ...Hash(N) tested by <R>, <R*R>, <Ri*Ri+1> gives the same result as for libc rand().
For string: i = TMath::Hash(string,nstring); For int: i = TMath::Hash(&intword,sizeof(int)); For pointer: i = TMath::Hash(&pointer,sizeof(void*));
V.Perev
This function is kept for back compatibility. The code previously in this function has been moved to the static function TString::Hash
| ULong_t TMath::Hash | ( | const char * | str | ) |
Calculates the Kolmogorov distribution function,.
\[ P(z) = 2 \sum_{j=1}^{\infty} (-1)^{j-1} e^{-2 j^2 z^2} \]
which gives the probability that Kolmogorov's test statistic will exceed the value z assuming the null hypothesis. This gives a very powerful test for comparing two one-dimensional distributions. see, for example, Eadie et al, "statistical Methods in Experimental Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where: z = dn*sqrt(n), and dn is the maximum deviation between a hypothetical distribution function and an experimental distribution with n events
NOTE: To compare two experimental distributions with m and n events, use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application. Probabilities less than 10^-15 are returned as zero. However, remember that the formula is only valid for "large" n. Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB.
| Double_t TMath::KolmogorovTest | ( | Int_t | na, |
| const Double_t * | a, | ||
| Int_t | nb, | ||
| const Double_t * | b, | ||
| Option_t * | option | ||
| ) |
Statistical test whether two one-dimensional sets of points are compatible with coming from the same parent distribution, using the Kolmogorov test.
That is, it is used to compare two experimental distributions of unbinned data.
Input: a,b: One-dimensional arrays of length na, nb, respectively. The elements of a and b must be given in ascending order. option is a character string to specify options "D" Put out a line of "Debug" printout "M" Return the Maximum Kolmogorov distance instead of prob
Output: The returned value prob is a calculated confidence level which gives a statistical test for compatibility of a and b. Values of prob close to zero are taken as indicating a small probability of compatibility. For two point sets drawn randomly from the same parent distribution, the value of prob should be uniformly distributed between zero and one. in case of error the function return -1 If the 2 sets have a different number of points, the minimum of the two sets is used.
Method: The Kolmogorov test is used. The test statistic is the maximum deviation between the two integrated distribution functions, multiplied by the normalizing factor (rdmax*sqrt(na*nb/(na+nb)).
Code adapted by Rene Brun from CERNLIB routine TKOLMO (Fred James) (W.T. Eadie, D. Drijard, F.E. James, M. Roos and B. Sadoulet, Statistical Methods in Experimental Physics, (North-Holland, Amsterdam 1971) 269-271)
The nuts-and-bolts of the TMath::KolmogorovTest() algorithm is a for-loop over the two sorted arrays a and b representing empirical distribution functions. The for-loop handles 3 cases: when the next points to be evaluated satisfy a>b, a<b, or a=b:
for (Int_t i=0;i<na+nb;i++) { if (a[ia-1] < b[ib-1]) { rdiff -= sa; ia++; if (ia > na) {ok = kTRUE; break;} } else if (a[ia-1] > b[ib-1]) { rdiff += sb; ib++; if (ib > nb) {ok = kTRUE; break;} } else { rdiff += sb - sa; ia++; ib++; if (ia > na) {ok = kTRUE; break;} if (ib > nb) {ok = kTRUE; break;} } rdmax = TMath::Max(rdmax,TMath::Abs(rdiff)); }
For the last case, a=b, the algorithm advances each array by one index in an attempt to move through the equality. However, this is incorrect when one or the other of a or b (or both) have a repeated value, call it x. For the KS statistic to be computed properly, rdiff needs to be calculated after all of the a and b at x have been tallied (this is due to the definition of the empirical distribution function; another way to convince yourself that the old CERNLIB method is wrong is that it implies that the function defined as the difference between a and b is multi-valued at x – besides being ugly, this would invalidate Kolmogorov's theorem).
The solution is to just add while-loops into the equality-case handling to perform the tally:
} else {
double x = a[ia-1];
while(a[ia-1] == x && ia <= na) {
rdiff -= sa;
ia++;
}
while(b[ib-1] == x && ib <= nb) {
rdiff += sb;
ib++;
}
if (ia > na) {ok = kTRUE; break;}
if (ib > nb) {ok = kTRUE; break;}
}
NOTE1 A good description of the Kolmogorov test can be seen at: http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
| Element TMath::KOrdStat | ( | Size | n, |
| const Element * | a, | ||
| Size | k, | ||
| Size * | work = 0 |
||
| ) |
The LANDAU function.
mu is a location parameter and correspond approximately to the most probable value and sigma is a scale parameter (not the sigma of the full distribution which is not defined) Note that for mu=0 and sigma=1 (default values) the exact location of the maximum of the distribution (most proper value) is at x = -0.22278 This function has been adapted from the CERNLIB routine G110 denlan. If norm=kTRUE (default is kFALSE) the result is divided by sigma
Computes the probability density function of Laplace distribution at point x, with location parameter alpha and shape parameter beta.
By default, alpha=0, beta=1 This distribution is known under different names, most common is double exponential distribution, but it also appears as the two-tailed exponential or the bilateral exponential distribution
Computes the distribution function of Laplace distribution at point x, with location parameter alpha and shape parameter beta.
By default, alpha=0, beta=1 This distribution is known under different names, most common is double exponential distribution, but it also appears as the two-tailed exponential or the bilateral exponential distribution
| Iterator TMath::LocMax | ( | Iterator | first, |
| Iterator | last | ||
| ) |
| Iterator TMath::LocMin | ( | Iterator | first, |
| Iterator | last | ||
| ) |
Computes the density of LogNormal distribution at point x.
Variable X has lognormal distribution if Y=Ln(X) has normal distribution
The formula was taken from "Engineering Statistics Handbook" on site http://www.itl.nist.gov/div898/handbook/eda/section3/eda3669.htm Implementation using ROOT::Math::lognormal_pdf
Definition at line 200 of file TMathBase.h.
Definition at line 203 of file TMathBase.h.
Definition at line 206 of file TMathBase.h.
Definition at line 209 of file TMathBase.h.
Definition at line 212 of file TMathBase.h.
Definition at line 215 of file TMathBase.h.
Definition at line 218 of file TMathBase.h.
Definition at line 221 of file TMathBase.h.
Definition at line 224 of file TMathBase.h.
Definition at line 227 of file TMathBase.h.
| T TMath::MaxElement | ( | Long64_t | n, |
| const T * | a | ||
| ) |
| Double_t TMath::Mean | ( | Iterator | first, |
| Iterator | last | ||
| ) |
| Double_t TMath::Mean | ( | Iterator | first, |
| Iterator | last, | ||
| WeightIterator | wfirst | ||
| ) |
Definition at line 168 of file TMathBase.h.
Definition at line 171 of file TMathBase.h.
Definition at line 174 of file TMathBase.h.
Definition at line 177 of file TMathBase.h.
Definition at line 180 of file TMathBase.h.
Definition at line 183 of file TMathBase.h.
Definition at line 186 of file TMathBase.h.
Definition at line 189 of file TMathBase.h.
Definition at line 192 of file TMathBase.h.
Definition at line 195 of file TMathBase.h.
| T TMath::MinElement | ( | Long64_t | n, |
| const T * | a | ||
| ) |
| T * TMath::Normal2Plane | ( | const T | v1[3], |
| const T | v2[3], | ||
| const T | v3[3], | ||
| T | normal[3] | ||
| ) |
Normalize a vector v in place.
Returns the norm of the original vector. This implementation (thanks Kevin Lynch krlynch@bu.edu) is protected against possible overflows.
|
inline |
Definition at line 103 of file TMathBase.h.
Simple recursive algorithm to find the permutations of n natural numbers, not necessarily all distinct adapted from CERNLIB routine PERMU.
The input array has to be initialised with a non descending sequence. The method returns kFALSE when all combinations are exhausted.
Compute the Poisson distribution function for (x,par) The Poisson PDF is implemented by means of Euler's Gamma-function (for the factorial), so for any x integer argument it is correct.
BUT for non-integer x values, it IS NOT equal to the Poisson distribution. see TMath::PoissonI to get a non-smooth function. Note that for large values of par, it is better to call
TMath::Gaus(x,par,sqrt(par),kTRUE)
compute the Poisson distribution function for (x,par) This is a non-smooth function.
This function is equivalent to ROOT::Math::poisson_pdf
|
inline |
|
inline |
|
inline |
Computation of the probability for a certain Chi-squared (chi2) and number of degrees of freedom (ndf).
Calculations are based on the incomplete gamma function P(a,x), where a=ndf/2 and x=chi2/2.
P(a,x) represents the probability that the observed Chi-squared for a correct model should be less than the value chi2.
The returned probability corresponds to 1-P(a,x), which denotes the probability that an observed Chi-squared exceeds the value chi2 by chance, even for a correct model.
| void TMath::Quantiles | ( | Int_t | n, |
| Int_t | nprob, | ||
| Double_t * | x, | ||
| Double_t * | quantiles, | ||
| Double_t * | prob, | ||
| Bool_t | isSorted = kTRUE, |
||
| Int_t * | index = 0, |
||
| Int_t | type = 7 |
||
| ) |
Computes sample quantiles, corresponding to the given probabilities Parameters: x -the data sample n - its size quantiles - computed quantiles are returned in there prob - probabilities where to compute quantiles nprob - size of prob array isSorted - is the input array x sorted? NOTE, that when the input is not sorted, an array of integers of size n needs to be allocated.
It can be passed by the user in parameter index, or, if not passed, it will be allocated inside the function
type - method to compute (from 1 to 9). Following types are provided: Discontinuous: type=1 - inverse of the empirical distribution function type=2 - like type 1, but with averaging at discontinuities type=3 - SAS definition: nearest even order statistic Piecwise linear continuous: In this case, sample quantiles can be obtained by linear interpolation between the k-th order statistic and p(k). type=4 - linear interpolation of empirical cdf, p(k)=k/n; type=5 - a very popular definition, p(k) = (k-0.5)/n; type=6 - used by Minitab and SPSS, p(k) = k/(n+1); type=7 - used by S-Plus and R, p(k) = (k-1)/(n-1); type=8 - resulting sample quantiles are approximately median unbiased regardless of the distribution of x. p(k) = (k-1/3)/(n+1/3); type=9 - resulting sample quantiles are approximately unbiased, when the sample comes from Normal distribution. p(k)=(k-3/8)/(n+1/4);
default type = 7
References: 1) Hyndman, R.J and Fan, Y, (1996) "Sample quantiles in statistical packages" American Statistician, 50, 361-365 2) R Project documentation for the function quantile of package {stats}
Definition at line 232 of file TMathBase.h.
Definition at line 235 of file TMathBase.h.
Definition at line 238 of file TMathBase.h.
Definition at line 241 of file TMathBase.h.
Definition at line 244 of file TMathBase.h.
| Double_t TMath::RMS | ( | Iterator | first, |
| Iterator | last | ||
| ) |
| Double_t TMath::RMS | ( | Iterator | first, |
| Iterator | last, | ||
| WeightIterator | wfirst | ||
| ) |
Calculates roots of polynomial of 3rd order a*x^3 + b*x^2 + c*x + d, where a == coef[3], b == coef[2], c == coef[1], d == coef[0] coef[3] must be different from 0 If the boolean returned by the method is false: ==> there are 3 real roots a,b,c If the boolean returned by the method is true: ==> there is one real root a and 2 complex conjugates roots (b+i*c,b-i*c)
Definition at line 153 of file TMathBase.h.
Definition at line 156 of file TMathBase.h.
Definition at line 159 of file TMathBase.h.
|
inline |
Definition at line 162 of file TMathBase.h.
|
inline |
Definition at line 137 of file TMathBase.h.
Definition at line 140 of file TMathBase.h.
Definition at line 143 of file TMathBase.h.
|
inline |
Definition at line 146 of file TMathBase.h.
| Double_t TMath::StdDev | ( | Iterator | first, |
| Iterator | last | ||
| ) |
| Double_t TMath::StdDev | ( | Iterator | first, |
| Iterator | last, | ||
| WeightIterator | wfirst | ||
| ) |
Computes density function for Student's t- distribution (the probability function (integral of density) is computed in StudentI).
First parameter stands for x - the actual variable of the density function p(x) and the point at which the density is calculated. Second parameter stands for number of degrees of freedom.
About Student distribution: Student's t-distribution is used for many significance tests, for example, for the Student's t-tests for the statistical significance of difference between two sample means and for confidence intervals for the difference between two population means.
Example: suppose we have a random sample of size n drawn from normal distribution with mean Mu and st.deviation Sigma. Then the variable
t = (sample_mean - Mu)/(sample_deviation / sqrt(n))
has Student's t-distribution with n-1 degrees of freedom.
NOTE that this function's second argument is number of degrees of freedom, not the sample size.
As the number of degrees of freedom grows, t-distribution approaches Normal(0,1) distribution. Implementation by Anna Kreshuk.
Calculates the cumulative distribution function of Student's t-distribution second parameter stands for number of degrees of freedom, not for the number of samples if x has Student's t-distribution, the function returns the probability of x being less than T.
Implementation by Anna Kreshuk.
Computes quantiles of the Student's t-distribution 1st argument is the probability, at which the quantile is computed 2nd argument - the number of degrees of freedom of the Student distribution When the 3rd argument lower_tail is kTRUE (default)- the algorithm returns such x0, that P(x < x0)=p upper tail (lower_tail is kFALSE)- the algorithm returns such x0, that P(x > x0)=p the algorithm was taken from G.W.Hill, "Algorithm 396, Student's t-quantiles" "Communications of the ACM", 13(10), October 1970.
Returns the value of the Vavilov density function Parameters: 1st - the point were the density function is evaluated 2nd - value of kappa (distribution parameter) 3rd - value of beta2 (distribution parameter) The algorithm was taken from the CernLib function vavden(G115) Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution Nucl.Instr.
and Meth. B47(1990), 215-224 Accuracy: quote from the reference above: "The resuls of our code have been compared with the values of the Vavilov density function computed numerically in an accurate way: our approximation shows a difference of less than 3% around the peak of the density function, slowly increasing going towards the extreme tails to the right and to the left"
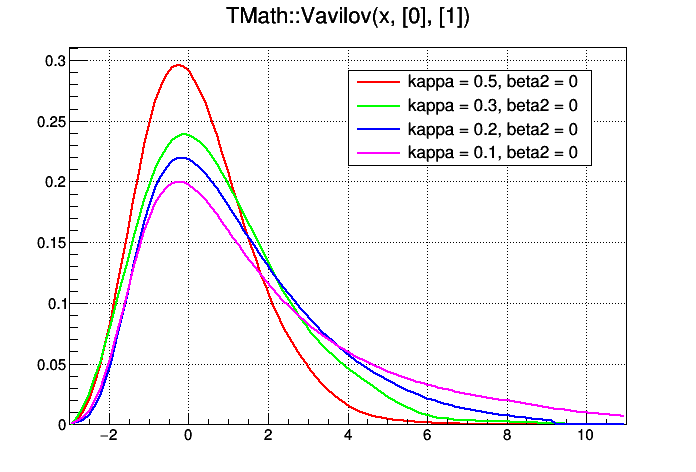
Returns the value of the Vavilov distribution function Parameters: 1st - the point were the density function is evaluated 2nd - value of kappa (distribution parameter) 3rd - value of beta2 (distribution parameter) The algorithm was taken from the CernLib function vavden(G115) Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution Nucl.Instr.
and Meth. B47(1990), 215-224 Accuracy: quote from the reference above: "The resuls of our code have been compared with the values of the Vavilov density function computed numerically in an accurate way: our approximation shows a difference of less than 3% around the peak of the density function, slowly increasing going towards the extreme tails to the right and to the left"
Computation of Voigt function (normalised).
Voigt is a convolution of gauss(xx) = 1/(sqrt(2*pi)*sigma) * exp(xx*xx/(2*sigma*sigma) and lorentz(xx) = (1/pi) * (lg/2) / (xx*xx + lg*lg/4) functions.
The Voigt function is known to be the real part of Faddeeva function also called complex error function [2].
The algoritm was developed by J. Humlicek [1]. This code is based on fortran code presented by R. J. Wells [2]. Translated and adapted by Miha D. Puc
To calculate the Faddeeva function with relative error less than 10^(-r). r can be set by the the user subject to the constraints 2 <= r <= 5.
[1] J. Humlicek, JQSRT, 21, 437 (1982). [2] R.J. Wells "Rapid Approximation to the Voigt/Faddeeva Function and its Derivatives" JQSRT 62 (1999), pp 29-48. http://www-atm.physics.ox.ac.uk/user/wells/voigt.html