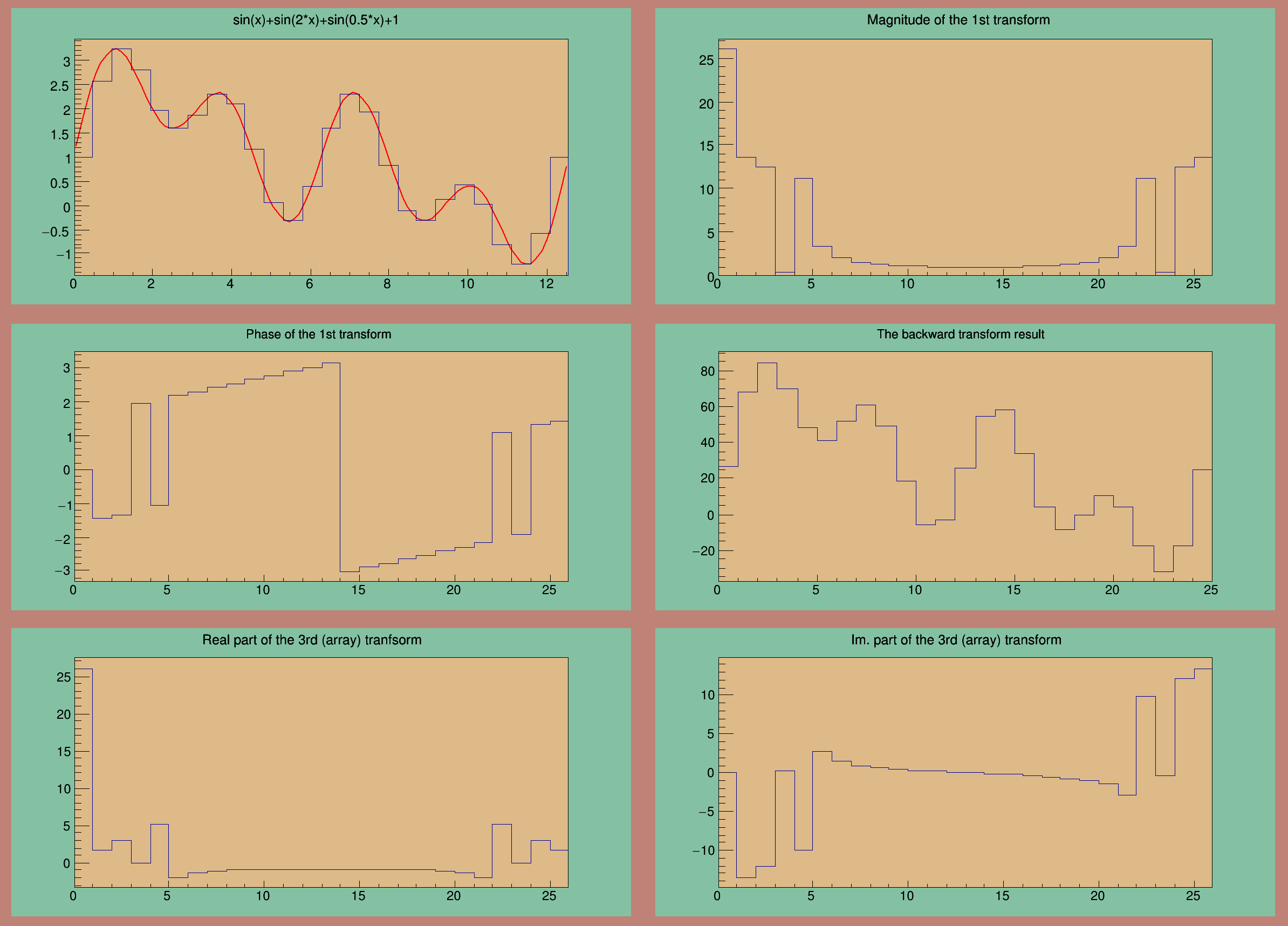
This tutorial illustrates the Fast Fourier Transforms interface in ROOT.
This tutorial illustrates the Fast Fourier Transforms interface in ROOT.
FFT transform types provided in ROOT:
- "C2CFORWARD" - a complex input/output discrete Fourier transform (DFT) in one or more dimensions, -1 in the exponent
- "C2CBACKWARD"- a complex input/output discrete Fourier transform (DFT) in one or more dimensions, +1 in the exponent
- "R2C" - a real-input/complex-output discrete Fourier transform (DFT) in one or more dimensions,
- "C2R" - inverse transforms to "R2C", taking complex input (storing the non-redundant half of a logically Hermitian array) to real output
- "R2HC" - a real-input DFT with output in "halfcomplex" format, i.e. real and imaginary parts for a transform of size n stored as r0, r1, r2, ..., rn/2, i(n+1)/2-1, ..., i2, i1
- "HC2R" - computes the reverse of FFTW_R2HC, above
- "DHT" - computes a discrete Hartley transform
Sine/cosine transforms:
- DCT-I (REDFT00 in FFTW3 notation)
- DCT-II (REDFT10 in FFTW3 notation)
- DCT-III(REDFT01 in FFTW3 notation)
- DCT-IV (REDFT11 in FFTW3 notation)
- DST-I (RODFT00 in FFTW3 notation)
- DST-II (RODFT10 in FFTW3 notation)
- DST-III(RODFT01 in FFTW3 notation)
- DST-IV (RODFT11 in FFTW3 notation)
First part of the tutorial shows how to transform the histograms Second part shows how to transform the data arrays directly
Processing /mnt/build/workspace/root-makedoc-v614/rootspi/rdoc/src/v6-14-00-patches/tutorials/fft/FFT.C...
1st transform: DC component: 26.000000
1st transform: Nyquist harmonic: -0.932840
2nd transform: DC component: 29.000000
2nd transform: Nyquist harmonic: -0.000000
void FFT()
{
TCanvas *myc =
new TCanvas(
"myc",
"Fast Fourier Transform", 800, 600);
TPad *c1_1 =
new TPad(
"c1_1",
"c1_1",0.01,0.67,0.49,0.99);
TPad *c1_2 =
new TPad(
"c1_2",
"c1_2",0.51,0.67,0.99,0.99);
TPad *c1_3 =
new TPad(
"c1_3",
"c1_3",0.01,0.34,0.49,0.65);
TPad *c1_4 =
new TPad(
"c1_4",
"c1_4",0.51,0.34,0.99,0.65);
TPad *c1_5 =
new TPad(
"c1_5",
"c1_5",0.01,0.01,0.49,0.32);
TPad *c1_6 =
new TPad(
"c1_6",
"c1_6",0.51,0.01,0.99,0.32);
TF1 *fsin =
new TF1(
"fsin",
"sin(x)+sin(2*x)+sin(0.5*x)+1", 0, 4*
TMath::Pi());
}
hm = hsin->
FFT(hm,
"MAG");
hm->
SetTitle(
"Magnitude of the 1st transform");
hp = hsin->
FFT(hp,
"PH");
hp->
SetTitle(
"Phase of the 1st transform");
printf("1st transform: DC component: %f\n", re);
printf("1st transform: Nyquist harmonic: %f\n", re);
hb->
SetTitle(
"The backward transform result");
delete fft_back;
fft_back=0;
}
if (!fft_own) return;
hr->
SetTitle(
"Real part of the 3rd (array) tranfsorm");
him->
SetTitle(
"Im. part of the 3rd (array) transform");
TF1 *fcos =
new TF1(
"fcos",
"cos(x)+cos(0.5*x)+cos(2*x)+1", 0, 4*
TMath::Pi());
}
printf("2nd transform: DC component: %f\n", re_2);
printf("2nd transform: Nyquist harmonic: %f\n", re_2);
delete fft_own;
delete [] in;
delete [] re_full;
delete [] im_full;
}
- Authors
- Anna Kreshuk, Jens Hoffmann
Definition in file FFT.C.



 This tutorial illustrates the Fast Fourier Transforms interface in ROOT.
This tutorial illustrates the Fast Fourier Transforms interface in ROOT.