TSVDUnfoldExample.C File Reference

Detailed Description

Data unfolding using Singular Value Decomposition

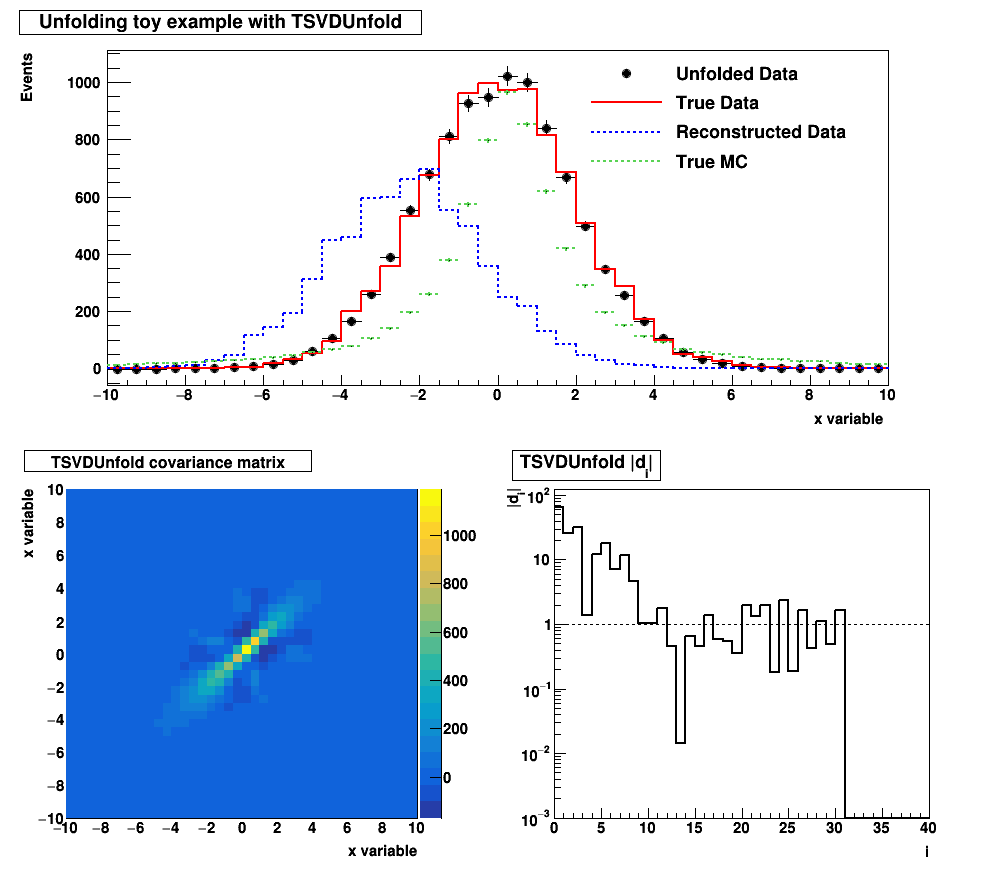
TSVDUnfold example

Data unfolding using Singular Value Decomposition (hep-ph/9509307)

Example distribution and smearing model from Tim Adye (RAL)

#include <iostream>

#include "TROOT.h"
#include "TSystem.h"
#include "TStyle.h"
#include "TRandom3.h"
#include "TString.h"
#include "TMath.h"
#include "TH1D.h"
#include "TH2D.h"
#include "TLegend.h"
#include "TCanvas.h"
#include "TColor.h"
#include "TLine.h"

#include "TSVDUnfold.h"


Double_t Reconstruct( Double_t xt, TRandom3& R )
{
   // apply some Gaussian smearing + bias and efficiency corrections to fake reconstruction
   const Double_t cutdummy = -99999.0;
   Double_t xeff = 0.3 + (1.0 - 0.3)/20.0*(xt + 10.0);  // efficiency
   Double_t x    = R.Rndm();
   if (x > xeff) return cutdummy;
   else {
     Double_t xsmear= R.Gaus(-2.5,0.2); // bias and smear
     return xt+xsmear;
   }
}

void TSVDUnfoldExample()
{
   gROOT->SetStyle("Plain");
   gStyle->SetOptStat(0);

   TRandom3 R;

   const Double_t cutdummy= -99999.0;

   // --------------------------------------
   // Data/MC toy generation
   //
   // The MC input
   Int_t nbins = 40;
   TH1D *xini = new TH1D("xini", "MC truth", nbins, -10.0, 10.0);
   TH1D *bini = new TH1D("bini", "MC reco", nbins, -10.0, 10.0);
   TH2D *Adet = new TH2D("Adet", "detector response", nbins, -10.0, 10.0, nbins, -10.0, 10.0);

   // Data
   TH1D *data = new TH1D("data", "data", nbins, -10.0, 10.0);
   // Data "truth" distribution to test the unfolding
   TH1D *datatrue = new TH1D("datatrue", "data truth", nbins, -10.0, 10.0);
   // Statistical covariance matrix
   TH2D *statcov = new TH2D("statcov", "covariance matrix", nbins, -10.0, 10.0, nbins, -10.0, 10.0);

   // Fill the MC using a Breit-Wigner, mean 0.3 and width 2.5.
   for (Int_t i= 0; i<100000; i++) {
      Double_t xt = R.BreitWigner(0.3, 2.5);
      xini->Fill(xt);
      Double_t x = Reconstruct( xt, R );
      if (x != cutdummy) {
         Adet->Fill(x, xt);
         bini->Fill(x);
      }
   }

   // Fill the "data" with a Gaussian, mean 0 and width 2.
   for (Int_t i=0; i<10000; i++) {
      Double_t xt = R.Gaus(0.0, 2.0);
      datatrue->Fill(xt);
      Double_t x = Reconstruct( xt, R );
      if (x != cutdummy)
      data->Fill(x);
   }

   cout << "Created toy distributions and errors for: " << endl;
   cout << "... \"true MC\"   and \"reconstructed (smeared) MC\"" << endl;
   cout << "... \"true data\" and \"reconstructed (smeared) data\"" << endl;
   cout << "... the \"detector response matrix\"" << endl;

   // Fill the data covariance matrix
   for (int i=1; i<=data->GetNbinsX(); i++) {
       statcov->SetBinContent(i,i,data->GetBinError(i)*data->GetBinError(i));
   }

   // ----------------------------
   // Here starts the actual unfolding
   //
   // Create TSVDUnfold object and initialise
   TSVDUnfold *tsvdunf = new TSVDUnfold( data, statcov, bini, xini, Adet );

   // It is possible to normalise unfolded spectrum to unit area
   tsvdunf->SetNormalize( kFALSE ); // no normalisation here

   // Perform the unfolding with regularisation parameter kreg = 13
   // - the larger kreg, the finer grained the unfolding, but the more fluctuations occur
   // - the smaller kreg, the stronger is the regularisation and the bias
   TH1D* unfres = tsvdunf->Unfold( 13 );

   // Get the distribution of the d to cross check the regularization
   // - choose kreg to be the point where |d_i| stop being statistically significantly >>1
   TH1D* ddist = tsvdunf->GetD();

   // Get the distribution of the singular values
   TH1D* svdist = tsvdunf->GetSV();

   // Compute the error matrix for the unfolded spectrum using toy MC
   // using the measured covariance matrix as input to generate the toys
   // 100 toys should usually be enough
   // The same method can be used for different covariance matrices separately.
   TH2D* ustatcov = tsvdunf->GetUnfoldCovMatrix( statcov, 100 );

   // Now compute the error matrix on the unfolded distribution originating
   // from the finite detector matrix statistics
   TH2D* uadetcov = tsvdunf->GetAdetCovMatrix( 100 );

   // Sum up the two (they are uncorrelated)
   ustatcov->Add( uadetcov );

   //Get the computed regularized covariance matrix (always corresponding to total uncertainty passed in constructor) and add uncertainties from finite MC statistics.
   TH2D* utaucov = tsvdunf->GetXtau();
   utaucov->Add( uadetcov );

   //Get the computed inverse of the covariance matrix
   TH2D* uinvcov = tsvdunf->GetXinv();


   // ---------------------------------
   // Only plotting stuff below
   
   for (int i=1; i<=unfres->GetNbinsX(); i++) {
      unfres->SetBinError(i, TMath::Sqrt(utaucov->GetBinContent(i,i)));
   }

   // Renormalize just to be able to plot on the same scale
   xini->Scale(0.7*datatrue->Integral()/xini->Integral());

   TLegend *leg = new TLegend(0.58,0.60,0.99,0.88);
   leg->SetBorderSize(0);
   leg->SetFillColor(0);
   leg->SetFillStyle(0);
   leg->AddEntry(unfres,"Unfolded Data","p");
   leg->AddEntry(datatrue,"True Data","l");
   leg->AddEntry(data,"Reconstructed Data","l");
   leg->AddEntry(xini,"True MC","l");

   TCanvas *c1 = new TCanvas( "c1", "Unfolding toy example with TSVDUnfold", 1000, 900 );

   c1->Divide(1,2);
   TVirtualPad * c11 = c1->cd(1);

   TH1D* frame = new TH1D( *unfres );
   frame->SetTitle( "Unfolding toy example with TSVDUnfold" );
   frame->GetXaxis()->SetTitle( "x variable" );
   frame->GetYaxis()->SetTitle( "Events" );
   frame->GetXaxis()->SetTitleOffset( 1.25 );
   frame->GetYaxis()->SetTitleOffset( 1.29 );
   frame->Draw();

   data->SetLineStyle(2);
   data->SetLineColor(4);
   data->SetLineWidth(2);
   unfres->SetMarkerStyle(20);
   datatrue->SetLineColor(2);
   datatrue->SetLineWidth(2);
   xini->SetLineStyle(2);
   xini->SetLineColor(8);
   xini->SetLineWidth(2);
   // ------------------------------------------------------------

   // add histograms
   unfres->Draw("same");
   datatrue->Draw("same");
   data->Draw("same");
   xini->Draw("same");

   leg->Draw();

   // covariance matrix
   TVirtualPad * c12 = c1->cd(2);
   c12->Divide(2,1);
   TVirtualPad * c2 = c12->cd(1);
   c2->SetRightMargin   ( 0.15         );

   TH2D* covframe = new TH2D( *ustatcov );
   covframe->SetTitle( "TSVDUnfold covariance matrix" );
   covframe->GetXaxis()->SetTitle( "x variable" );
   covframe->GetYaxis()->SetTitle( "x variable" );
   covframe->GetXaxis()->SetTitleOffset( 1.25 );
   covframe->GetYaxis()->SetTitleOffset( 1.29 );
   covframe->Draw();

   ustatcov->SetLineWidth( 2 );
   ustatcov->Draw( "colzsame" );

   // distribution of the d quantity
   TVirtualPad * c3 = c12->cd(2);
   c3->SetLogy();

   TLine *line = new TLine( 0.,1.,40.,1. );
   line->SetLineStyle(2);

   TH1D* dframe = new TH1D( *ddist );
   dframe->SetTitle( "TSVDUnfold |d_{i}|" );
   dframe->GetXaxis()->SetTitle( "i" );
   dframe->GetYaxis()->SetTitle( "|d_{i}|" );
   dframe->GetXaxis()->SetTitleOffset( 1.25 );
   dframe->GetYaxis()->SetTitleOffset( 1.29 );
   dframe->SetMinimum( 0.001 );
   dframe->Draw();

   ddist->SetLineWidth( 2 );
   ddist->Draw( "same" );
   line->Draw();
}

Authors

Kerstin Tackmann, Andreas Hoecker, Heiko Lacker

Definition in file TSVDUnfoldExample.C.