Logo ROOT   6.14/05
Reference Guide
testUnfold1.C File Reference
Tutorials » TUnfold tutorials

Detailed Description

View in nbviewer Open in SWAN Test program for the classes TUnfold and related.

  1. Generate Monte Carlo and Data events The events consist of signal background

    The signal is a resonance. It is generated with a Breit-Wigner, smeared by a Gaussian

  2. Unfold the data. The result is: The background level The shape of the resonance, corrected for detector effects

    Systematic errors from the MC shape variation are included and propagated to the result

  3. fit the unfolded distribution, including the correlation matrix
  4. save six plots to a file testUnfold1.ps
    1 2 3
    4 5 6
    1. 2d-plot of the matrix describing the migrations
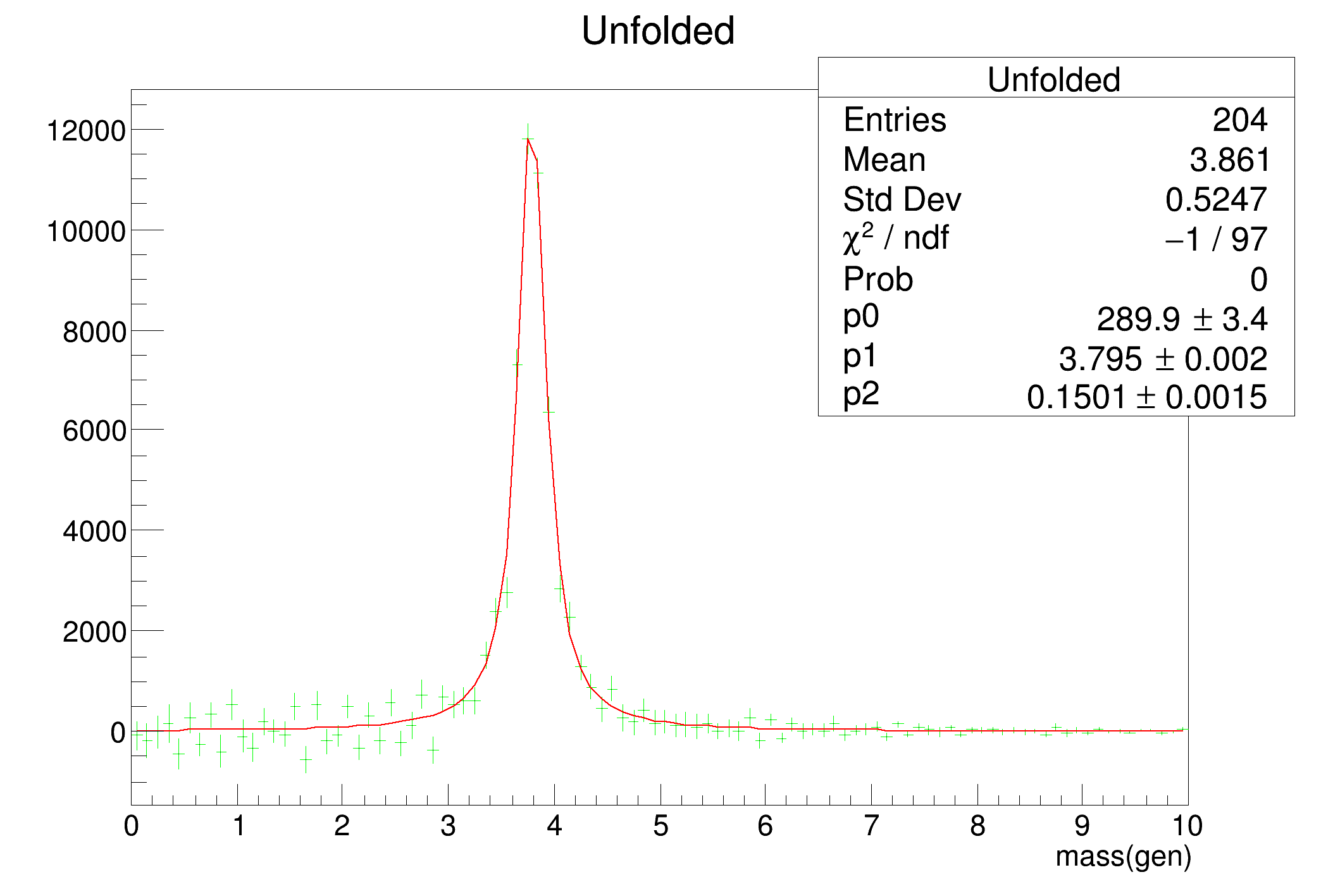
    2. generator-level distributions
      • blue: unfolded data, total errors
      • green: unfolded data, statistical errors
      • red: generated data
      • black: fit to green data points
    3. detector level distributions
      • blue: unfolded data, folded back through the matrix
      • black: Monte Carlo (with wrong peal position)
      • blue: data
    4. global correlation coefficients
    5. \( \chi^2 \) as a function of \( log(\tau) \) the star indicates the final choice of \( \tau \)
    6. the L curve
0.0209980010986
7.82071614265
Processing /mnt/build/workspace/root-makedoc-v614/rootspi/rdoc/src/v6-14-00-patches/tutorials/unfold/testUnfold1.C...
tau=5.56618e-05
chi**2=173.079+9.63005 / 147
chi**2(sys)=147.813
FCN=99.8432 FROM MINOS STATUS=SUCCESSFUL 20 CALLS 190 TOTAL
EDM=4.83442e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.89860e+02 3.42457e+00 -1.98917e-03 -1.05299e-04
2 p1 3.79532e+00 1.74788e-03 1.06465e-06 -3.36308e-03
3 p2 1.50090e-01 1.46316e-03 1.46316e-03 -3.31677e-02
(int) 0
pict1_testUnfold1.C.png
#include <TError.h>
#include <TMath.h>
#include <TCanvas.h>
#include <TRandom3.h>
#include <TFitter.h>
#include <TF1.h>
#include <TStyle.h>
#include <TVector.h>
#include <TGraph.h>
#include "TUnfoldDensity.h"
// #define VERBOSE_LCURVE_SCAN
using namespace std;
TRandom *rnd=0;
TH2 *gHistInvEMatrix;
TVirtualFitter *gFitter=0;
void chisquare_corr(Int_t &npar, Double_t * /*gin */, Double_t &f, Double_t *u, Int_t /*flag */) {
// Minimization function for H1s using a Chisquare method
// only one-dimensional histograms are supported
// Correlated errors are taken from an external inverse covariance matrix
// stored in a 2-dimensional histogram
Double_t x;
TH1 *hfit = (TH1*)gFitter->GetObjectFit();
TF1 *f1 = (TF1*)gFitter->GetUserFunc();
f1->InitArgs(&x,u);
npar = f1->GetNpar();
f = 0;
Int_t npfit = 0;
Int_t nPoints=hfit->GetNbinsX();
Double_t *df=new Double_t[nPoints];
for (Int_t i=0;i<nPoints;i++) {
x = hfit->GetBinCenter(i+1);
TF1::RejectPoint(kFALSE);
df[i] = f1->EvalPar(&x,u)-hfit->GetBinContent(i+1);
if (TF1::RejectedPoint()) df[i]=0.0;
else npfit++;
}
for (Int_t i=0;i<nPoints;i++) {
for (Int_t j=0;j<nPoints;j++) {
f += df[i]*df[j]*gHistInvEMatrix->GetBinContent(i+1,j+1);
}
}
delete[] df;
f1->SetNumberFitPoints(npfit);
}
Double_t bw_func(Double_t *x,Double_t *par) {
Double_t dm=x[0]-par[1];
return par[0]/(dm*dm+par[2]*par[2]);
}
// generate an event
// output:
// negative mass: background event
// positive mass: signal event
Double_t GenerateEvent(Double_t bgr, // relative fraction of background
Double_t mass, // peak position
Double_t gamma) // peak width
{
Double_t t;
if(rnd->Rndm()>bgr) {
// generate signal event
// with positive mass
do {
do {
t=rnd->Rndm();
} while(t>=1.0);
t=TMath::Tan((t-0.5)*TMath::Pi())*gamma+mass;
} while(t<=0.0);
return t;
} else {
// generate background event
// generate events following a power-law distribution
// f(E) = K * TMath::power((E0+E),N0)
static Double_t const E0=2.4;
static Double_t const N0=2.9;
do {
do {
t=rnd->Rndm();
} while(t>=1.0);
// the mass is returned negative
// In our example a convenient way to indicate it is a background event.
t= -(TMath::Power(1.-t,1./(1.-N0))-1.0)*E0;
} while(t>=0.0);
return t;
}
}
// smear the event to detector level
// input:
// mass on generator level (mTrue>0 !)
// output:
// mass on detector level
Double_t DetectorEvent(Double_t mTrue) {
// smear by double-gaussian
static Double_t frac=0.1;
static Double_t wideBias=0.03;
static Double_t wideSigma=0.5;
static Double_t smallBias=0.0;
static Double_t smallSigma=0.1;
if(rnd->Rndm()>frac) {
return rnd->Gaus(mTrue+smallBias,smallSigma);
} else {
return rnd->Gaus(mTrue+wideBias,wideSigma);
}
}
int testUnfold1()
{
// switch on histogram errors
TH1::SetDefaultSumw2();
// show fit result
gStyle->SetOptFit(1111);
// random generator
rnd=new TRandom3();
// data and MC luminosity, cross-section
Double_t const luminosityData=100000;
Double_t const luminosityMC=1000000;
Double_t const crossSection=1.0;
Int_t const nDet=250;
Int_t const nGen=100;
Double_t const xminDet=0.0;
Double_t const xmaxDet=10.0;
Double_t const xminGen=0.0;
Double_t const xmaxGen=10.0;
//============================================
// generate MC distribution
//
TH1D *histMgenMC=new TH1D("MgenMC",";mass(gen)",nGen,xminGen,xmaxGen);
TH1D *histMdetMC=new TH1D("MdetMC",";mass(det)",nDet,xminDet,xmaxDet);
TH2D *histMdetGenMC=new TH2D("MdetgenMC",";mass(det);mass(gen)",
nDet,xminDet,xmaxDet,nGen,xminGen,xmaxGen);
Int_t neventMC=rnd->Poisson(luminosityMC*crossSection);
for(Int_t i=0;i<neventMC;i++) {
Double_t mGen=GenerateEvent(0.3, // relative fraction of background
4.0, // peak position in MC
0.2); // peak width in MC
Double_t mDet=DetectorEvent(TMath::Abs(mGen));
// the generated mass is negative for background
// and positive for signal
// so it will be filled in the underflow bin
// this is very convenient for the unfolding:
// the unfolded result will contain the number of background
// events in the underflow bin
// generated MC distribution (for comparison only)
histMgenMC->Fill(mGen,luminosityData/luminosityMC);
// reconstructed MC distribution (for comparison only)
histMdetMC->Fill(mDet,luminosityData/luminosityMC);
// matrix describing how the generator input migrates to the
// reconstructed level. Unfolding input.
// NOTE on underflow/overflow bins:
// (1) the detector level under/overflow bins are used for
// normalisation ("efficiency" correction)
// in our toy example, these bins are populated from tails
// of the initial MC distribution.
// (2) the generator level underflow/overflow bins are
// unfolded. In this example:
// underflow bin: background events reconstructed in the detector
// overflow bin: signal events generated at masses > xmaxDet
// for the unfolded result these bins will be filled
// -> the background normalisation will be contained in the underflow bin
histMdetGenMC->Fill(mDet,mGen,luminosityData/luminosityMC);
}
//============================================
// generate alternative MC
// this will be used to derive a systematic error due to MC
// parameter uncertainties
TH2D *histMdetGenSysMC=new TH2D("MdetgenSysMC",";mass(det);mass(gen)",
nDet,xminDet,xmaxDet,nGen,xminGen,xmaxGen);
neventMC=rnd->Poisson(luminosityMC*crossSection);
for(Int_t i=0;i<neventMC;i++) {
Double_t mGen=GenerateEvent
(0.5, // relative fraction of background
3.6, // peak position in MC with systematic shift
0.15); // peak width in MC
Double_t mDet=DetectorEvent(TMath::Abs(mGen));
histMdetGenSysMC->Fill(mDet,mGen,luminosityData/luminosityMC);
}
//============================================
// generate data distribution
//
TH1D *histMgenData=new TH1D("MgenData",";mass(gen)",nGen,xminGen,xmaxGen);
TH1D *histMdetData=new TH1D("MdetData",";mass(det)",nDet,xminDet,xmaxDet);
Int_t neventData=rnd->Poisson(luminosityData*crossSection);
for(Int_t i=0;i<neventData;i++) {
Double_t mGen=GenerateEvent(0.4, // relative fraction of background
3.8, // peak position in data
0.15); // peak width in data
Double_t mDet=DetectorEvent(TMath::Abs(mGen));
// generated data mass for comparison plots
// for real data, we do not have this histogram
histMgenData->Fill(mGen);
// reconstructed mass, unfolding input
histMdetData->Fill(mDet);
}
//=========================================================================
// divide by bin width to get density distributions
TH1D *histDensityGenData=new TH1D("DensityGenData",";mass(gen)",
nGen,xminGen,xmaxGen);
TH1D *histDensityGenMC=new TH1D("DensityGenMC",";mass(gen)",
nGen,xminGen,xmaxGen);
for(Int_t i=1;i<=nGen;i++) {
histDensityGenData->SetBinContent(i,histMgenData->GetBinContent(i)/
histMgenData->GetBinWidth(i));
histDensityGenMC->SetBinContent(i,histMgenMC->GetBinContent(i)/
histMgenMC->GetBinWidth(i));
}
//=========================================================================
// set up the unfolding
// define migration matrix
TUnfoldDensity unfold(histMdetGenMC,TUnfold::kHistMapOutputVert);
// define input and bias scheme
// do not use the bias, because MC peak may be at the wrong place
// watch out for error codes returned by the SetInput method
// errors larger or equal 10000 are fatal:
// the data points specified as input are not sufficient to constrain the
// unfolding process
if(unfold.SetInput(histMdetData)>=10000) {
std::cout<<"Unfolding result may be wrong\n";
}
//========================================================================
// the unfolding is done here
//
// scan L curve and find best point
Int_t nScan=30;
// use automatic L-curve scan: start with taumin=taumax=0.0
Double_t tauMin=0.0;
Double_t tauMax=0.0;
Int_t iBest;
TSpline *logTauX,*logTauY;
TGraph *lCurve;
// if required, report Info messages (for debugging the L-curve scan)
#ifdef VERBOSE_LCURVE_SCAN
Int_t oldinfo=gErrorIgnoreLevel;
gErrorIgnoreLevel=kInfo;
#endif
// this method scans the parameter tau and finds the kink in the L curve
// finally, the unfolding is done for the best choice of tau
iBest=unfold.ScanLcurve(nScan,tauMin,tauMax,&lCurve,&logTauX,&logTauY);
// if required, switch to previous log-level
#ifdef VERBOSE_LCURVE_SCAN
gErrorIgnoreLevel=oldinfo;
#endif
//==========================================================================
// define a correlated systematic error
// for example, assume there is a 10% correlated error for all reconstructed
// masses larger than 7
Double_t SYS_ERROR1_MSTART=6;
Double_t SYS_ERROR1_SIZE=0.1;
TH2D *histMdetGenSys1=new TH2D("Mdetgensys1",";mass(det);mass(gen)",
nDet,xminDet,xmaxDet,nGen,xminGen,xmaxGen);
for(Int_t i=0;i<=nDet+1;i++) {
if(histMdetData->GetBinCenter(i)>=SYS_ERROR1_MSTART) {
for(Int_t j=0;j<=nGen+1;j++) {
histMdetGenSys1->SetBinContent(i,j,SYS_ERROR1_SIZE);
}
}
}
unfold.AddSysError(histMdetGenSysMC,"SYSERROR_MC",TUnfold::kHistMapOutputVert,
TUnfoldSys::kSysErrModeMatrix);
unfold.AddSysError(histMdetGenSys1,"SYSERROR1",TUnfold::kHistMapOutputVert,
TUnfoldSys::kSysErrModeRelative);
//==========================================================================
// print some results
//
std::cout<<"tau="<<unfold.GetTau()<<"\n";
std::cout<<"chi**2="<<unfold.GetChi2A()<<"+"<<unfold.GetChi2L()
<<" / "<<unfold.GetNdf()<<"\n";
std::cout<<"chi**2(sys)="<<unfold.GetChi2Sys()<<"\n";
//==========================================================================
// create graphs with one point to visualize the best choice of tau
//
Double_t t[1],x[1],y[1];
logTauX->GetKnot(iBest,t[0],x[0]);
logTauY->GetKnot(iBest,t[0],y[0]);
TGraph *bestLcurve=new TGraph(1,x,y);
TGraph *bestLogTauLogChi2=new TGraph(1,t,x);
//==========================================================================
// retrieve results into histograms
// get unfolded distribution
TH1 *histMunfold=unfold.GetOutput("Unfolded");
// get unfolding result, folded back
TH1 *histMdetFold=unfold.GetFoldedOutput("FoldedBack");
// get error matrix (input distribution [stat] errors only)
// TH2D *histEmatData=unfold.GetEmatrix("EmatData");
// get total error matrix:
// migration matrix uncorrelated and correlated systematic errors
// added in quadrature to the data statistical errors
TH2 *histEmatTotal=unfold.GetEmatrixTotal("EmatTotal");
// create data histogram with the total errors
TH1D *histTotalError=
new TH1D("TotalError",";mass(gen)",nGen,xminGen,xmaxGen);
for(Int_t bin=1;bin<=nGen;bin++) {
histTotalError->SetBinContent(bin,histMunfold->GetBinContent(bin));
histTotalError->SetBinError
(bin,TMath::Sqrt(histEmatTotal->GetBinContent(bin,bin)));
}
// get global correlation coefficients
// for this calculation one has to specify whether the
// underflow/overflow bins are included or not
// default: include all bins
// here: exclude underflow and overflow bins
TH1 *histRhoi=unfold.GetRhoItotal("rho_I",
0, // use default title
0, // all distributions
"*[UO]", // discard underflow and overflow bins on all axes
kTRUE, // use original binning
&gHistInvEMatrix // store inverse of error matrix
);
//======================================================================
// fit Breit-Wigner shape to unfolded data, using the full error matrix
// here we use a "user" chi**2 function to take into account
// the full covariance matrix
gFitter=TVirtualFitter::Fitter(histMunfold);
gFitter->SetFCN(chisquare_corr);
TF1 *bw=new TF1("bw",bw_func,xminGen,xmaxGen,3);
bw->SetParameter(0,1000.);
bw->SetParameter(1,3.8);
bw->SetParameter(2,0.2);
// for (wrong!) fitting without correlations, drop the option "U"
// here.
histMunfold->Fit(bw,"UE");
//=====================================================================
// plot some histograms
TCanvas output;
output.Divide(3,2);
// Show the matrix which connects input and output
// There are overflow bins at the bottom, not shown in the plot
// These contain the background shape.
// The overflow bins to the left and right contain
// events which are not reconstructed. These are necessary for proper MC
// normalisation
output.cd(1);
histMdetGenMC->Draw("BOX");
// draw generator-level distribution:
// data (red) [for real data this is not available]
// MC input (black) [with completely wrong peak position and shape]
// unfolded data (blue)
output.cd(2);
histTotalError->SetLineColor(kBlue);
histTotalError->Draw("E");
histMunfold->SetLineColor(kGreen);
histMunfold->Draw("SAME E1");
histDensityGenData->SetLineColor(kRed);
histDensityGenData->Draw("SAME");
histDensityGenMC->Draw("SAME HIST");
// show detector level distributions
// data (red)
// MC (black) [with completely wrong peak position and shape]
// unfolded data (blue)
output.cd(3);
histMdetFold->SetLineColor(kBlue);
histMdetFold->Draw();
histMdetMC->Draw("SAME HIST");
TH1 *histInput=unfold.GetInput("Minput",";mass(det)");
histInput->SetLineColor(kRed);
histInput->Draw("SAME");
// show correlation coefficients
output.cd(4);
histRhoi->Draw();
// show tau as a function of chi**2
output.cd(5);
logTauX->Draw();
bestLogTauLogChi2->SetMarkerColor(kRed);
bestLogTauLogChi2->Draw("*");
// show the L curve
output.cd(6);
lCurve->Draw("AL");
bestLcurve->SetMarkerColor(kRed);
bestLcurve->Draw("*");
output.SaveAs("testUnfold1.ps");
return 0;
}

Version 17.6, in parallel to changes in TUnfold

History:

This file is part of TUnfold.

TUnfold is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

TUnfold is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with TUnfold. If not, see http://www.gnu.org/licenses/.

Author
Stefan Schmitt DESY, 14.10.2008

Definition in file testUnfold1.C.