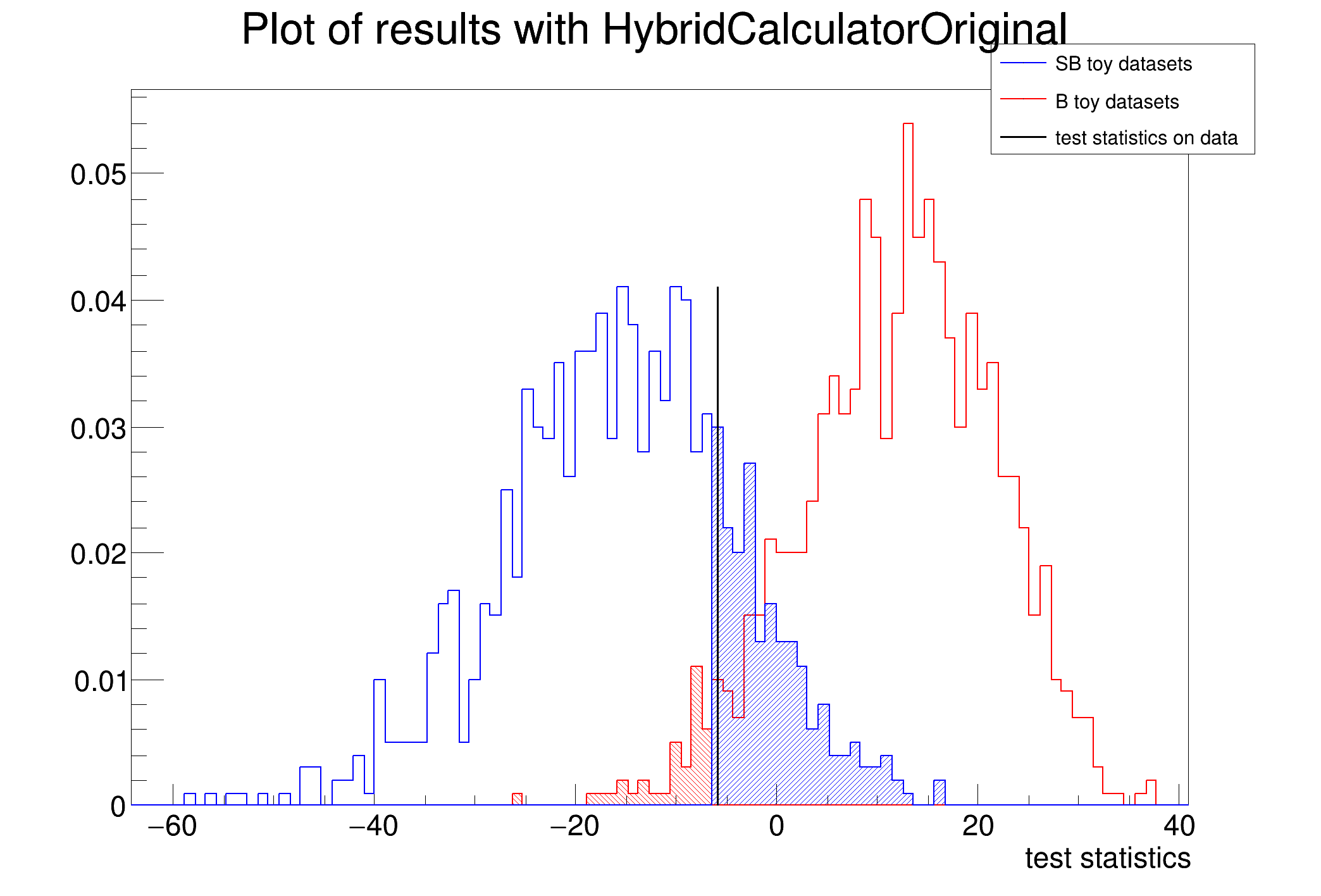
With this example, you should get: CL_sb = 0.130 and CL_b = 0.946 (if data had -2lnQ = -3.0742).
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
Test statistics has been evaluated for data
HybridCalculatorOriginal: run 1000 toy-MC experiments
with test statistics index: 1
marginalize nuisance parameters
....... toy number 0 / 1000
....... toy number 500 / 1000
Completed HybridCalculatorOriginal example:
- -2lnQ = -5.97789
- CL_sb = 0.194
- CL_b = 0.04
- CL_s = 4.85
- significance of data = 1.75069
- mean significance of toys = 2.65207
void HybridOriginalDemo(int ntoys = 1000)
{
RooGaussian sig_pdf(
"sig_pdf",
"",
x, RooConst(0.0), RooConst(0.8));
RooRealVar sig_yield(
"sig_yield",
"", 20, 0, 300);
RooRealVar bkg_yield(
"bkg_yield",
"", 40, 0, 300);
RooExtendPdf bkg_ext_pdf(
"bkg_ext_pdf",
"", bkg_pdf, bkg_yield);
sig_yield.setConstant(
kTRUE);
RooGaussian bkg_yield_prior(
"bkg_yield_prior",
"", bkg_yield, RooConst(bkg_yield.getVal()), RooConst(10.));
myHybridCalc.SetTestStatistic(1);
myHybridCalc.SetNumberOfToys(ntoys);
myHybridCalc.UseNuisance(true);
myHybridCalc.SetGenerateBinned(false);
if (!myHybridResult) {
std::cerr << "\nError returned from Hypothesis test" << std::endl;
return;
}
myHybridResult->
GetPlot(
"myHybridPlot",
"Plot of results with HybridCalculatorOriginal", 100);
double clsb_data = myHybridResult->
CLsplusb();
double clb_data = myHybridResult->
CLb();
double cls_data = myHybridResult->
CLs();
double mean_sb_toys_test_stat = myHybridPlot->
GetSBmean();
std::cout << "Completed HybridCalculatorOriginal example:\n";
std::cout << " - -2lnQ = " << min2lnQ_data << endl;
std::cout << " - CL_sb = " << clsb_data << std::endl;
std::cout << " - CL_b = " << clb_data << std::endl;
std::cout << " - CL_s = " << cls_data << std::endl;
std::cout << " - significance of data = " << data_significance << std::endl;
std::cout << " - mean significance of toys = " << toys_significance << std::endl;
}
RooAddPdf is an efficient implementation of a sum of PDFs of the form.
RooArgList is a container object that can hold multiple RooAbsArg objects.
RooArgSet is a container object that can hold multiple RooAbsArg objects.
RooDataSet is a container class to hold unbinned data.
RooExtendPdf is a wrapper around an existing PDF that adds a parameteric extended likelihood term to ...
RooPolynomial implements a polynomial p.d.f of the form.
static TRandom * randomGenerator()
Return a pointer to a singleton random-number generator implementation.
RooRealVar represents a variable that can be changed from the outside.
HybridCalculatorOriginal class.
This class provides the plots for the result of a study performed with the HybridCalculatorOriginal c...
double GetSBmean()
Get SB histo mean.
void Draw(const char *options="")
Draw on current pad.
Class encapsulating the result of the HybridCalculatorOriginal.
double GetTestStat_data()
Get test statistics value for data.
HybridPlot * GetPlot(const char *name, const char *title, int n_bins)
prepare a plot showing a result and return a pointer to a HybridPlot object the needed arguments are:...
void SetDataTestStatistics(double testStat_data_val)
set the value of the test statistics on data
virtual Double_t CLb() const
Convert NullPValue into a "confidence level".
virtual Double_t CLsplusb() const
Convert AlternatePValue into a "confidence level".
virtual Double_t Significance() const
familiar name for the Null p-value in terms of 1-sided Gaussian significance
virtual Double_t CLs() const
is simply (not a method, but a quantity)
virtual void SetSeed(ULong_t seed=0)
Set the random generator seed.
RooCmdArg Extended(Bool_t flag=kTRUE)
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...
Namespace for the RooStats classes.

 Example on how to use the HybridCalculatorOriginal class
Example on how to use the HybridCalculatorOriginal class