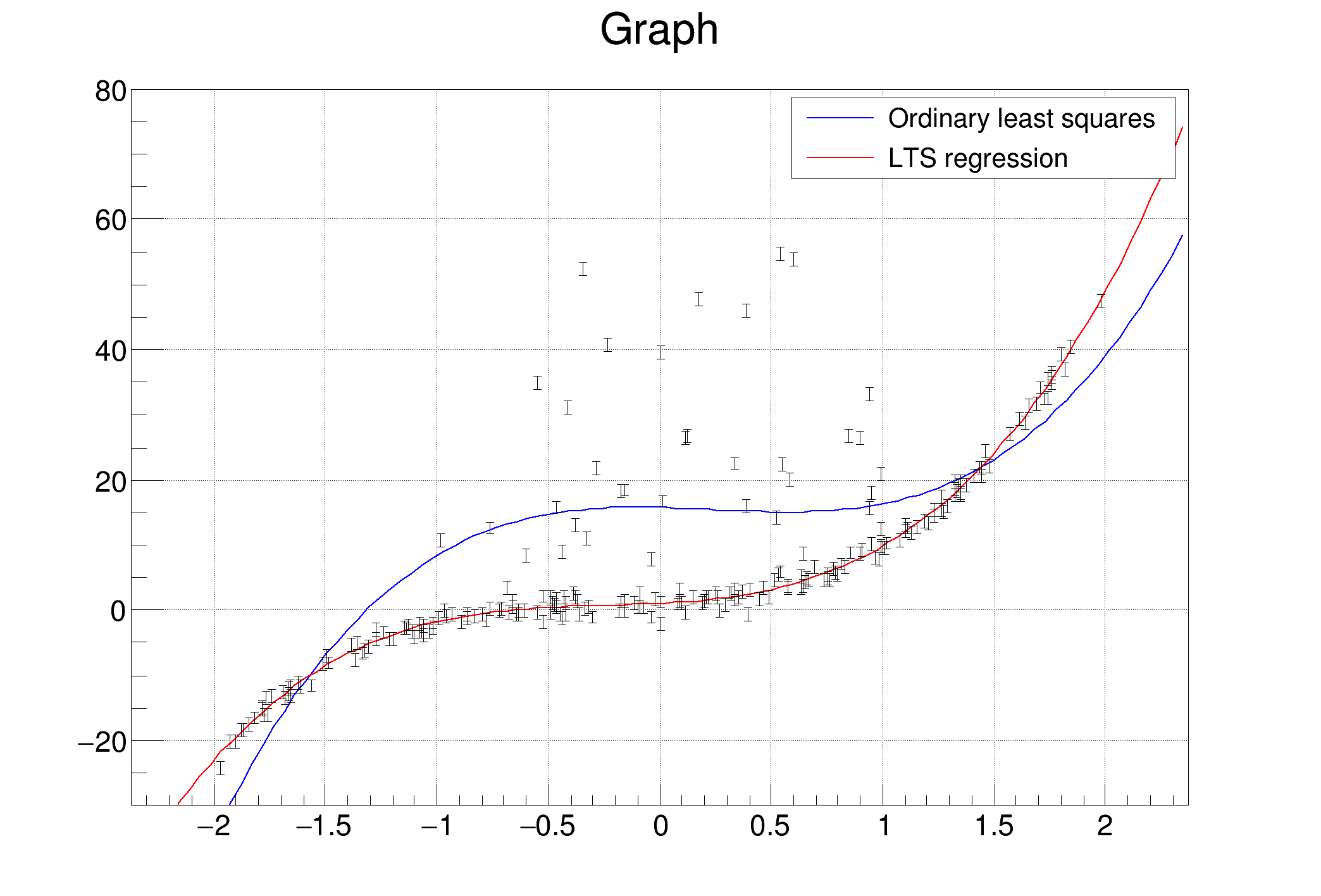
This tutorial shows how the least trimmed squares regression, included in the TLinearFitter class, can be used for fitting in cases when the data contains outliers.
This tutorial shows how the least trimmed squares regression, included in the TLinearFitter class, can be used for fitting in cases when the data contains outliers.
Here the fitting is done via the TGraph::Fit function with option "rob": If you want to use the linear fitter directly for computing the robust fitting coefficients, just use the TLinearFitter::EvalRobust function instead of TLinearFitter::Eval
Ordinary least squares:
****************************************
Minimizer is Linear / Migrad
Chi2 = 606758
NDf = 246
p0 = 15.724 +/- 0.0887641
p1 = -0.835912 +/- 0.14096
p2 = -3.40616 +/- 0.0607296
p3 = 4.82569 +/- 0.0602628
Resistant Least trimmed squares fit:
****************************************
Minimizer is Linear / Robust (h=0.75)
Chi2 = 634792
NDf = 246
p0 = 1.00953
p1 = 1.71148
p2 = 2.97937
p3 = 4.07752
void fitLinearRobust()
{
for (i=0; i<fraction; i++){
y[i]=1 + 2*
x[i] + 3*
x[i]*
x[i] + 4*
x[i]*
x[i]*
x[i] +
e[i]*
r.Gaus();
}
for (i=fraction; i<npoints; i++){
y[i] = 1 + 2*
x[i] + 3*
x[i]*
x[i] + 4*
x[i]*
x[i]*
x[i] +
r.Landau(10, 5);
}
TF1 *ffit1 =
new TF1(
"ffit1",
"pol3", -5, 5);
TF1 *ffit2 =
new TF1(
"ffit2",
"pol3", -5, 5);
TCanvas *myc =
new TCanvas(
"myc",
"Linear and robust linear fitting");
printf("Ordinary least squares:\n");
printf("Resistant Least trimmed squares fit:\n");
grr->
Fit(ffit2,
"+rob=0.75");
leg->AddEntry(ffit1,
"Ordinary least squares",
"l");
leg->AddEntry(ffit2,
"LTS regression",
"l");
}
virtual void SetLineColor(Color_t lcolor)
Set the line color.
A TGraphErrors is a TGraph with error bars.
virtual void SetMaximum(Double_t maximum=-1111)
Set the maximum of the graph.
virtual TFitResultPtr Fit(const char *formula, Option_t *option="", Option_t *goption="", Axis_t xmin=0, Axis_t xmax=0)
Fit this graph with function with name fname.
virtual void Draw(Option_t *chopt="")
Draw this graph with its current attributes.
virtual void SetMinimum(Double_t minimum=-1111)
Set the minimum of the graph.
This class displays a legend box (TPaveText) containing several legend entries.
void SetGrid(Int_t valuex=1, Int_t valuey=1) override
This is the base class for the ROOT Random number generators.
- Author
- Anna Kreshuk
Definition in file fitLinearRobust.C.

 This tutorial shows how the least trimmed squares regression, included in the TLinearFitter class, can be used for fitting in cases when the data contains outliers.
This tutorial shows how the least trimmed squares regression, included in the TLinearFitter class, can be used for fitting in cases when the data contains outliers.