Logo ROOT  

Reference Guide
 
Loading...
Searching...
No Matches
rf610_visualerror.C File Reference
Tutorials » RooFit Tutorials

Detailed Description

View in nbviewer Open in SWAN Likelihood and minimization: visualization of errors from a covariance matrix

␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- The following expressions will be evaluated in cache-and-track mode: (sig,bkg)
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 fsig 3.30000e-01 1.00000e-01 0.00000e+00 1.00000e+00
2 m 0.00000e+00 2.00000e+00 -1.00000e+01 1.00000e+01
3 m2 -1.00000e+00 2.00000e+00 -1.00000e+01 1.00000e+01
4 s 2.00000e+00 5.00000e-01 1.00000e+00 5.00000e+01
5 s2 6.00000e+00 2.50000e+00 1.00000e+00 5.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 2500 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=2770.05 FROM MIGRAD STATUS=INITIATE 20 CALLS 21 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 fsig 3.30000e-01 1.00000e-01 2.14988e-01 -9.80006e+00
2 m 0.00000e+00 2.00000e+00 2.01358e-01 -3.95919e+01
3 m2 -1.00000e+00 2.00000e+00 2.02430e-01 3.98515e+01
4 s 2.00000e+00 5.00000e-01 7.46809e-02 2.95415e+01
5 s2 6.00000e+00 2.50000e+00 1.74125e-01 4.56667e+01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2767.65 FROM MIGRAD STATUS=CONVERGED 125 CALLS 126 TOTAL
EDM=1.56678e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 fsig 2.98883e-01 6.74303e-02 2.39863e-03 7.00359e-03
2 m 3.08816e-01 2.09098e-01 6.83546e-04 -2.93512e-02
3 m2 -1.31219e+00 3.64277e-01 9.46152e-04 8.97852e-02
4 s 1.78229e+00 2.51997e-01 9.25951e-04 -2.49363e-02
5 s2 5.51197e+00 4.85498e-01 6.94615e-04 1.27501e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 5 ERR DEF=0.5
4.580e-03 -3.800e-03 -1.557e-02 1.331e-02 2.642e-02
-3.800e-03 4.373e-02 -3.141e-03 -1.195e-02 -2.959e-02
-1.557e-02 -3.141e-03 1.328e-01 -4.509e-02 -1.100e-01
1.331e-02 -1.195e-02 -4.509e-02 6.354e-02 7.253e-02
2.642e-02 -2.959e-02 -1.100e-01 7.253e-02 2.358e-01
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5
1 0.89430 1.000 -0.269 -0.632 0.780 0.804
2 0.43384 -0.269 1.000 -0.041 -0.227 -0.291
3 0.70478 -0.632 -0.041 1.000 -0.491 -0.621
4 0.78303 0.780 -0.227 -0.491 1.000 0.593
5 0.82883 0.804 -0.291 -0.621 0.593 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 2500
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2767.65 FROM HESSE STATUS=OK 31 CALLS 157 TOTAL
EDM=1.56685e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 fsig 2.98883e-01 6.78952e-02 4.79727e-04 -4.13956e-01
2 m 3.08816e-01 2.09026e-01 1.36709e-04 3.08865e-02
3 m2 -1.31219e+00 3.67042e-01 1.89230e-04 -1.31599e-01
4 s 1.78229e+00 2.53102e-01 1.85190e-04 -1.31741e+00
5 s2 5.51197e+00 4.89300e-01 1.38923e-04 -9.54177e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 5 ERR DEF=0.5
4.644e-03 -3.811e-03 -1.596e-02 1.350e-02 2.692e-02
-3.811e-03 4.370e-02 -2.970e-03 -1.206e-02 -2.967e-02
-1.596e-02 -2.970e-03 1.348e-01 -4.619e-02 -1.129e-01
1.350e-02 -1.206e-02 -4.619e-02 6.410e-02 7.402e-02
2.692e-02 -2.967e-02 -1.129e-01 7.402e-02 2.395e-01
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5
1 0.89584 1.000 -0.268 -0.638 0.782 0.807
2 0.43319 -0.268 1.000 -0.039 -0.228 -0.290
3 0.71012 -0.638 -0.039 1.000 -0.497 -0.628
4 0.78518 0.782 -0.228 -0.497 1.000 0.597
5 0.83175 0.807 -0.290 -0.628 0.597 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
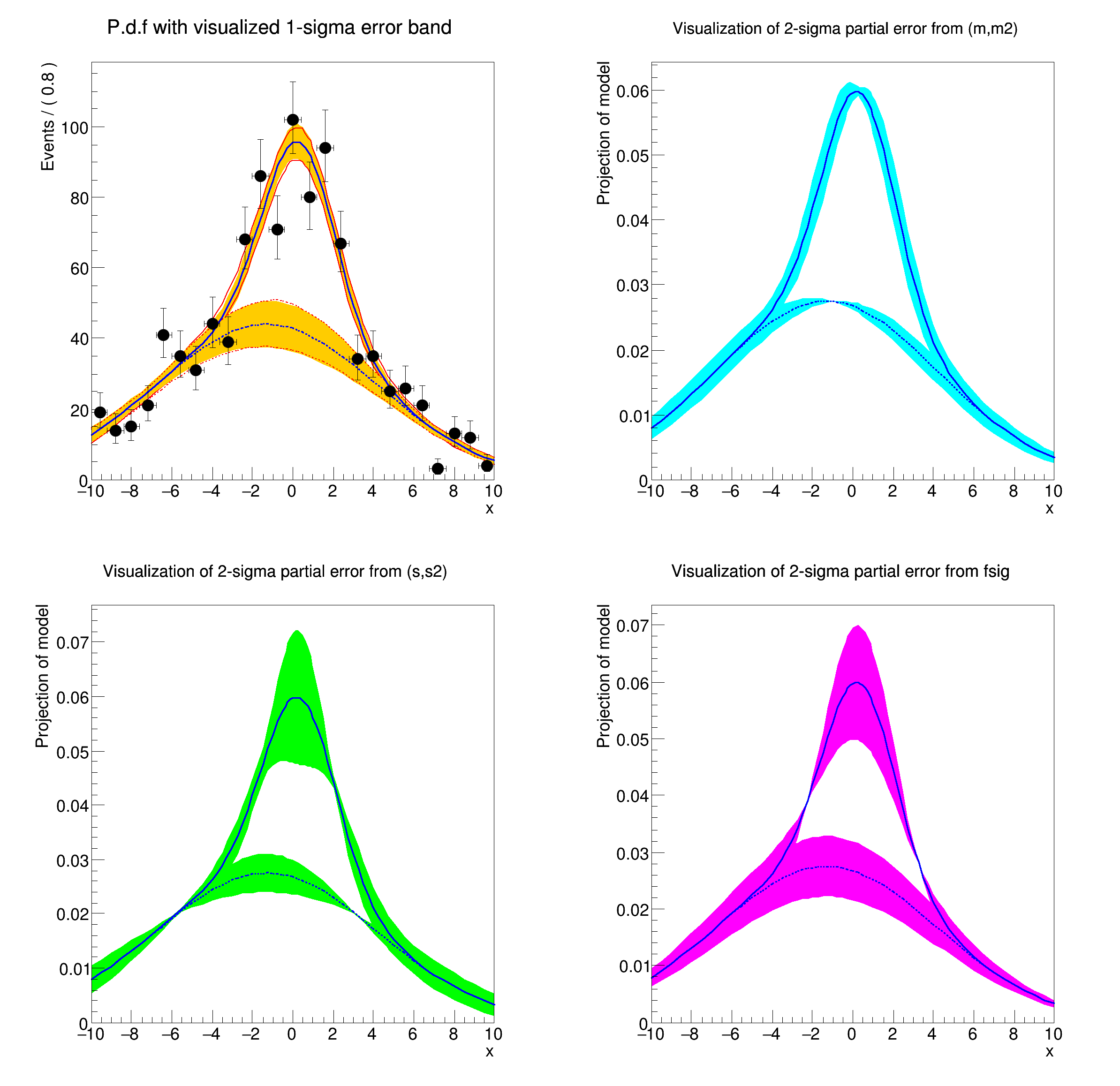
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) INFO: visualizing 1-sigma uncertainties in parameters (m,s,fsig,m2,s2) from fit result fitresult_model_genData using 315 samplings.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) INFO: visualizing 1-sigma uncertainties in parameters (m,s,fsig,m2,s2) from fit result fitresult_model_genData using 315 samplings.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#0] WARNING:Plotting -- Fill color or style was set for plotting "model", but these only have an effect when 'DrawOption("F")' for fill is used at the same time.
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) directly selected PDF components: (bkg)
[#1] INFO:Plotting -- RooAbsPdf::plotOn(model) indirectly selected PDF components: ()
#include "RooRealVar.h"
#include "RooDataHist.h"
#include "RooGaussian.h"
#include "RooConstVar.h"
#include "RooAddPdf.h"
#include "RooPlot.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "TAxis.h"
using namespace RooFit;
void rf610_visualerror()
{
// S e t u p e x a m p l e f i t
// ---------------------------------------
// Create sum of two Gaussians pdf with factory
RooRealVar x("x", "x", -10, 10);
RooRealVar m("m", "m", 0, -10, 10);
RooRealVar s("s", "s", 2, 1, 50);
RooGaussian sig("sig", "sig", x, m, s);
RooRealVar m2("m2", "m2", -1, -10, 10);
RooRealVar s2("s2", "s2", 6, 1, 50);
RooGaussian bkg("bkg", "bkg", x, m2, s2);
RooRealVar fsig("fsig", "fsig", 0.33, 0, 1);
RooAddPdf model("model", "model", RooArgList(sig, bkg), fsig);
// Create binned dataset
x.setBins(25);
RooAbsData *d = model.generateBinned(x, 1000);
// Perform fit and save fit result
RooFitResult *r = model.fitTo(*d, Save());
// V i s u a l i z e f i t e r r o r
// -------------------------------------
// Make plot frame
RooPlot *frame = x.frame(Bins(40), Title("P.d.f with visualized 1-sigma error band"));
d->plotOn(frame);
// Visualize 1-sigma error encoded in fit result 'r' as orange band using linear error propagation
// This results in an error band that is by construction symmetric
//
// The linear error is calculated as
// error(x) = Z* F_a(x) * Corr(a,a') F_a'(x)
//
// where F_a(x) = [ f(x,a+da) - f(x,a-da) ] / 2,
//
// with f(x) = the plotted curve
// 'da' = error taken from the fit result
// Corr(a,a') = the correlation matrix from the fit result
// Z = requested significance 'Z sigma band'
//
// The linear method is fast (required 2*N evaluations of the curve, where N is the number of parameters),
// but may not be accurate in the presence of strong correlations (~>0.9) and at Z>2 due to linear and
// Gaussian approximations made
//
model.plotOn(frame, VisualizeError(*r, 1), FillColor(kOrange));
// Calculate error using sampling method and visualize as dashed red line.
//
// In this method a number of curves is calculated with variations of the parameter values, as sampled
// from a multi-variate Gaussian pdf that is constructed from the fit results covariance matrix.
// The error(x) is determined by calculating a central interval that capture N% of the variations
// for each value of x, where N% is controlled by Z (i.e. Z=1 gives N=68%). The number of sampling curves
// is chosen to be such that at least 100 curves are expected to be outside the N% interval, and is minimally
// 100 (e.g. Z=1->Ncurve=356, Z=2->Ncurve=2156)) Intervals from the sampling method can be asymmetric,
// and may perform better in the presence of strong correlations, but may take (much) longer to calculate
model.plotOn(frame, VisualizeError(*r, 1, kFALSE), DrawOption("L"), LineWidth(2), LineColor(kRed));
// Perform the same type of error visualization on the background component only.
// The VisualizeError() option can generally applied to _any_ kind of plot (components, asymmetries, efficiencies
// etc..)
model.plotOn(frame, VisualizeError(*r, 1), FillColor(kOrange), Components("bkg"));
model.plotOn(frame, VisualizeError(*r, 1, kFALSE), DrawOption("L"), LineWidth(2), LineColor(kRed), Components("bkg"),
LineStyle(kDashed));
// Overlay central value
model.plotOn(frame);
model.plotOn(frame, Components("bkg"), LineStyle(kDashed));
d->plotOn(frame);
frame->SetMinimum(0);
// V i s u a l i z e p a r t i a l f i t e r r o r
// ------------------------------------------------------
// Make plot frame
RooPlot *frame2 = x.frame(Bins(40), Title("Visualization of 2-sigma partial error from (m,m2)"));
// Visualize partial error. For partial error visualization the covariance matrix is first reduced as follows
// ___ -1
// Vred = V22 = V11 - V12 * V22 * V21
//
// Where V11,V12,V21,V22 represent a block decomposition of the covariance matrix into observables that
// are propagated (labeled by index '1') and that are not propagated (labeled by index '2'), and V22bar
// is the Shur complement of V22, calculated as shown above
//
// (Note that Vred is _not_ a simple sub-matrix of V)
// Propagate partial error due to shape parameters (m,m2) using linear and sampling method
model.plotOn(frame2, VisualizeError(*r, RooArgSet(m, m2), 2), FillColor(kCyan));
model.plotOn(frame2, Components("bkg"), VisualizeError(*r, RooArgSet(m, m2), 2), FillColor(kCyan));
model.plotOn(frame2);
model.plotOn(frame2, Components("bkg"), LineStyle(kDashed));
frame2->SetMinimum(0);
// Make plot frame
RooPlot *frame3 = x.frame(Bins(40), Title("Visualization of 2-sigma partial error from (s,s2)"));
// Propagate partial error due to yield parameter using linear and sampling method
model.plotOn(frame3, VisualizeError(*r, RooArgSet(s, s2), 2), FillColor(kGreen));
model.plotOn(frame3, Components("bkg"), VisualizeError(*r, RooArgSet(s, s2), 2), FillColor(kGreen));
model.plotOn(frame3);
model.plotOn(frame3, Components("bkg"), LineStyle(kDashed));
frame3->SetMinimum(0);
// Make plot frame
RooPlot *frame4 = x.frame(Bins(40), Title("Visualization of 2-sigma partial error from fsig"));
// Propagate partial error due to yield parameter using linear and sampling method
model.plotOn(frame4, VisualizeError(*r, RooArgSet(fsig), 2), FillColor(kMagenta));
model.plotOn(frame4, Components("bkg"), VisualizeError(*r, RooArgSet(fsig), 2), FillColor(kMagenta));
model.plotOn(frame4);
model.plotOn(frame4, Components("bkg"), LineStyle(kDashed));
frame4->SetMinimum(0);
TCanvas *c = new TCanvas("rf610_visualerror", "rf610_visualerror", 800, 800);
c->Divide(2, 2);
c->cd(1);
gPad->SetLeftMargin(0.15);
frame->GetYaxis()->SetTitleOffset(1.4);
frame->Draw();
c->cd(2);
gPad->SetLeftMargin(0.15);
frame2->GetYaxis()->SetTitleOffset(1.6);
frame2->Draw();
c->cd(3);
gPad->SetLeftMargin(0.15);
frame3->GetYaxis()->SetTitleOffset(1.6);
frame3->Draw();
c->cd(4);
gPad->SetLeftMargin(0.15);
frame4->GetYaxis()->SetTitleOffset(1.6);
frame4->Draw();
}
r
ROOT::R::TRInterface & r
Definition Object.C:4
d
#define d(i)
Definition RSha256.hxx:102
c
#define c(i)
Definition RSha256.hxx:101
kFALSE
const Bool_t kFALSE
Definition RtypesCore.h:92
kRed
@ kRed
Definition Rtypes.h:66
kOrange
@ kOrange
Definition Rtypes.h:67
kGreen
@ kGreen
Definition Rtypes.h:66
kMagenta
@ kMagenta
Definition Rtypes.h:66
kCyan
@ kCyan
Definition Rtypes.h:66
kDashed
@ kDashed
Definition TAttLine.h:48
gPad
#define gPad
Definition TVirtualPad.h:287
RooAbsData
RooAbsData is the common abstract base class for binned and unbinned datasets.
Definition RooAbsData.h:49
RooAddPdf
RooAddPdf is an efficient implementation of a sum of PDFs of the form.
Definition RooAddPdf.h:32
RooArgList
RooArgList is a container object that can hold multiple RooAbsArg objects.
Definition RooArgList.h:21
RooArgSet
RooArgSet is a container object that can hold multiple RooAbsArg objects.
Definition RooArgSet.h:29
RooFitResult
RooFitResult is a container class to hold the input and output of a PDF fit to a dataset.
Definition RooFitResult.h:40
RooGaussian
Plain Gaussian p.d.f.
Definition RooGaussian.h:24
RooPlot
A RooPlot is a plot frame and a container for graphics objects within that frame.
Definition RooPlot.h:44
RooPlot::SetMinimum
virtual void SetMinimum(Double_t minimum=-1111)
Set minimum value of Y axis.
Definition RooPlot.cxx:1091
RooPlot::GetYaxis
TAxis * GetYaxis() const
Definition RooPlot.cxx:1263
RooPlot::frame
static RooPlot * frame(const RooAbsRealLValue &var, Double_t xmin, Double_t xmax, Int_t nBins)
Create a new frame for a given variable in x.
Definition RooPlot.cxx:249
RooPlot::Draw
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
Definition RooPlot.cxx:691
RooRealVar
RooRealVar represents a variable that can be changed from the outside.
Definition RooRealVar.h:39
TAttAxis::SetTitleOffset
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title.
Definition TAttAxis.cxx:293
TCanvas
The Canvas class.
Definition TCanvas.h:23
x
Double_t x[n]
Definition legend1.C:17
RooFit
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...
Definition RooCFunction1Binding.h:29
rf610_visualerror
Definition rf610_visualerror.py:1
m
auto * m
Definition textangle.C:8
Date
April 2009
Author
Wouter Verkerke

Definition in file rf610_visualerror.C.