␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 alpha 5.00000e+00 9.90000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 500 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=35708.9 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 alpha 5.00000e+00 9.90000e-01 2.01369e-01 1.02940e+02
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=35708.6 FROM MIGRAD STATUS=CONVERGED 12 CALLS 13 TOTAL
EDM=1.24247e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 alpha 4.96355e+00 4.16961e-02 1.10376e-03 -4.18389e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
1.739e-03
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 500
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=35708.6 FROM HESSE STATUS=OK 5 CALLS 18 TOTAL
EDM=1.24183e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 alpha 4.96355e+00 4.16961e-02 2.20752e-04 -1.74664e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
1.739e-03
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 mean2 1.00000e+01 5.00000e+00 0.00000e+00 2.00000e+02
2 sigma 3.00000e+00 9.90000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=5148.93 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mean2 1.00000e+01 5.00000e+00 1.18625e-01 -5.23438e+03
2 sigma 3.00000e+00 9.90000e-01 2.22742e-01 -7.90389e+03
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2551.39 FROM MIGRAD STATUS=CONVERGED 59 CALLS 60 TOTAL
EDM=8.7852e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mean2 1.00100e+02 1.98019e+00 6.89576e-04 4.58015e-02
2 sigma 3.11719e+00 7.12427e-02 5.29831e-04 1.79331e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
3.922e+00 2.826e-03
2.826e-03 5.076e-03
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.02003 1.000 0.020
2 0.02003 0.020 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2551.39 FROM HESSE STATUS=OK 10 CALLS 70 TOTAL
EDM=8.78617e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 mean2 1.00100e+02 1.98016e+00 1.37915e-04 1.00004e-03
2 sigma 3.11719e+00 7.12418e-02 1.05966e-04 -4.01138e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
3.922e+00 2.730e-03
2.730e-03 5.076e-03
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.01935 1.000 0.019
2 0.01935 0.019 1.000
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
RooFitResult: minimized FCN value: 2551.39, estimated distance to minimum: 8.78617e-06
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
mean2 1.0010e+02 +/- 1.98e+00
sigma 3.1172e+00 +/- 7.12e-02

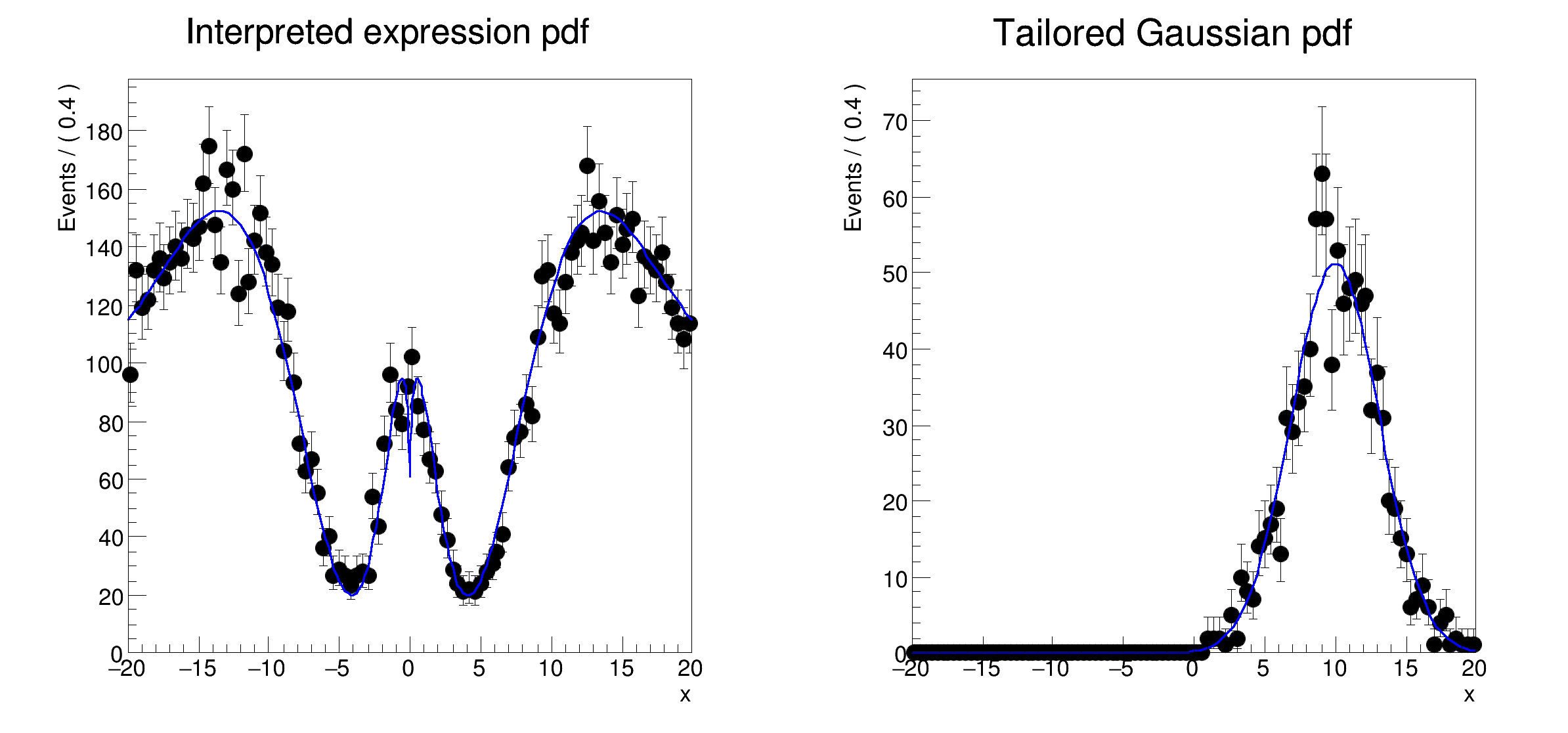
 Basic functionality: interpreted functions and PDFs.
Basic functionality: interpreted functions and PDFs.