This tutorial requires FFT3 to be enabled.
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Eval -- RooRealVar::setRange(mean) new range named 'refrange_fft_model' created with bounds [-3,3]
[#0] WARNING:Eval -- The FFT convolution 'model' will run with 50 bins. A decent accuracy for difficult convolutions is typically only reached with n >= 1000. Suggest to increase the number of bins of the observable 'mean'.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(gx_Int[mean,x]) using numeric integrator RooIntegrator1D to calculate Int(mean)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_mean_Int[mean]) using numeric integrator RooIntegrator1D to calculate Int(mean)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(model) creating new cache 0x5597a6382380 with pdf gx_CONV_model_mean_CACHE_Obs[x,mean]_NORM_x_mean for nset (x,mean) with code 0
[#0] WARNING:Eval -- The FFT convolution 'model' will run with 50 bins. A decent accuracy for difficult convolutions is typically only reached with n >= 1000. Suggest to increase the number of bins of the observable 'mean'.
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(model) creating new cache 0x5597a6ec0c80 with pdf gx_CONV_model_mean_CACHE_Obs[x,mean]_NORM_x_mean for nset (x,mean) with code 0 from preexisting content.
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#0] WARNING:Minimization -- RooAbsMinimizerFcn::synchronize: WARNING: no initial error estimate available for a: using 0.5
[#0] WARNING:Minimization -- RooAbsMinimizerFcn::synchronize: WARNING: no initial error estimate available for sigma: using 0.2
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a 2.00000e+00 5.00000e-01 1.00000e+00 1.00000e+01
2 sigma 5.00000e-01 2.00000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
prevFCN = 2171.275755 START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
a=2.012, sigma=0.5, [#1] INFO:NumericIntegration -- RooRealIntegral::init(gx_Int[mean,x]) using numeric integrator RooIntegrator1D to calculate Int(mean)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_mean_Int[mean]) using numeric integrator RooIntegrator1D to calculate Int(mean)
prevFCN = 2171.275755 a=1.988,
prevFCN = 2171.275755 a=2.121,
prevFCN = 2171.861215 a=1.886,
prevFCN = 2172.184717 a=2.012,
prevFCN = 2171.275755 a=1.988,
prevFCN = 2171.275755 a=2, sigma=0.5047,
prevFCN = 2171.286528 sigma=0.4953,
prevFCN = 2171.267762 sigma=0.5029,
prevFCN = 2171.281998 sigma=0.4971,
prevFCN = 2171.270547 a=2.012, sigma=0.5,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.012,
prevFCN = 2171.275755 a=2.121,
prevFCN = 2171.861215 a=1.886,
prevFCN = 2172.184717 a=2.012,
prevFCN = 2171.275755 a=1.988,
prevFCN = 2171.275755 a=2.121,
prevFCN = 2171.861215 a=1.886,
prevFCN = 2172.184717 a=2, sigma=0.5029,
prevFCN = 2171.281998 sigma=0.4971,
prevFCN = 2171.270547 FCN=2171.28 FROM MIGRAD STATUS=INITIATE 29 CALLS 30 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 2.00000e+00 5.00000e-01 0.00000e+00 -3.89301e+00
2 sigma 5.00000e-01 2.00000e-01 0.00000e+00 3.88521e+00
ERR DEF= 0.5
a=2.013, sigma=0.4843,
prevFCN = 2171.259881 a=2.009, sigma=0.4884,
prevFCN = 2171.260992 a=2.025, sigma=0.4843,
prevFCN = 2171.259881 a=2.001,
prevFCN = 2171.259881 a=2.134,
prevFCN = 2171.692149 a=1.898,
prevFCN = 2172.378568 a=2.025,
prevFCN = 2171.259881 a=2.001,
prevFCN = 2171.259881 a=2.013, sigma=0.4871,
prevFCN = 2171.26042 sigma=0.4815,
prevFCN = 2171.260367 MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
sigma=0.4843,
prevFCN = 2171.259881 MINUIT WARNING IN HESSE
============== Second derivative enters zero, param 1
a=2.025,
prevFCN = 2171.259881 a=2.001,
prevFCN = 2171.259881 a=2.134,
prevFCN = 2171.692149 a=1.898,
prevFCN = 2172.378568 a=2.013, sigma=0.4871,
prevFCN = 2171.26042 sigma=0.4815,
prevFCN = 2171.260367 a=2.015, sigma=0.4843,
prevFCN = 2171.259881 a=2.011,
prevFCN = 2171.259881 a=2.013, sigma=0.4848,
prevFCN = 2171.259907 sigma=0.4837,
prevFCN = 2171.259896 a=2.134, sigma=0.4871,
prevFCN = 2171.720718 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2171.26 FROM HESSE STATUS=OK 12 CALLS 52 TOTAL
EDM=0.0753125 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 2.01276e+00 1.33301e-01 4.15492e-02 -8.26033e+00
2 sigma 4.84270e-01 1.23533e-01 1.47360e-03 1.78734e-02
ERR DEF= 0.5
a=2.065, sigma=0.4512,
prevFCN = 2171.332894 a=2.03, sigma=0.473,
prevFCN = 2171.26812 a=2.02, sigma=0.4794,
prevFCN = 2171.261381 a=2.016, sigma=0.482,
prevFCN = 2171.260198 a=2.014, sigma=0.4832,
prevFCN = 2171.25995 a=2.014, sigma=0.4837,
prevFCN = 2171.259895 a=2.013, sigma=0.484,
prevFCN = 2171.259883 a=2.013, sigma=0.4841,
prevFCN = 2171.259881 a=2.013, sigma=0.4842,
prevFCN = 2171.25988 a=2.025,
prevFCN = 2171.25988 a=2.001,
prevFCN = 2171.25988 a=2.134,
prevFCN = 2171.691427 a=1.898,
prevFCN = 2172.379556 a=2.025,
prevFCN = 2171.25988 a=2.001,
prevFCN = 2171.25988 a=2.013, sigma=0.487,
prevFCN = 2171.260398 sigma=0.4814,
prevFCN = 2171.260398 MIGRAD MINIMIZATION HAS CONVERGED.
FCN=2171.26 FROM MIGRAD STATUS=CONVERGED 68 CALLS 69 TOTAL
EDM=6.7408e-11 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 75.5 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 2.01287e+00 6.17567e-03 3.89434e-05 0.00000e+00
2 sigma 4.84198e-01 8.78354e-02 -3.78079e-05 1.79608e-04
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
3.814e-05 -2.915e-07
-2.915e-07 7.720e-03
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00054 1.000 -0.001
2 0.00054 -0.001 1.000
sigma=0.4842, **********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
prevFCN = 2171.25988 MINUIT WARNING IN HESSE
============== Second derivative enters zero, param 1
a=2.025,
prevFCN = 2171.25988 a=2.001,
prevFCN = 2171.25988 a=2.134,
prevFCN = 2171.691427 a=1.898,
prevFCN = 2172.379556 a=2.013, sigma=0.487,
prevFCN = 2171.260398 sigma=0.4814,
prevFCN = 2171.260398 a=2.015, sigma=0.4842,
prevFCN = 2171.25988 a=2.011,
prevFCN = 2171.25988 a=2.013, sigma=0.4848,
prevFCN = 2171.259901 sigma=0.4836,
prevFCN = 2171.259901 sigma=0.4843,
prevFCN = 2171.259881 sigma=0.4841,
prevFCN = 2171.259881 a=2.134, sigma=0.487,
prevFCN = 2171.720107 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2171.26 FROM HESSE STATUS=OK 14 CALLS 83 TOTAL
EDM=0.150733 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a 2.01287e+00 1.33303e-01 4.15492e-02 -8.86586e-01
2 sigma 4.84198e-01 1.23531e-01 1.48033e-03 -1.17421e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.778e-02 -1.158e-02
-1.158e-02 1.528e-02
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.70265 1.000 -0.703
2 0.70265 -0.703 1.000
a=2.013, sigma=0.4842, [#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#0] WARNING:Eval -- The FFT convolution 'model' will run with 50 bins. A decent accuracy for difficult convolutions is typically only reached with n >= 1000. Suggest to increase the number of bins of the observable 'mean'.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(gx_Int[mean,x]) using numeric integrator RooIntegrator1D to calculate Int(mean)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_mean_Int[mean]) using numeric integrator RooIntegrator1D to calculate Int(mean)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(model) creating new cache 0x5597a722dba0 with pdf gx_CONV_model_mean_CACHE_Obs[x,mean]_NORM_x_mean for nset (x,mean) with code 0
[#0] WARNING:Eval -- The FFT convolution 'model' will run with 50 bins. A decent accuracy for difficult convolutions is typically only reached with n >= 1000. Suggest to increase the number of bins of the observable 'mean'.
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(model) creating new cache 0x5597a722dba0 with pdf gx_CONV_model_mean_CACHE_Obs[x,mean]_NORM_x for nset (x) with code 0 from preexisting content.

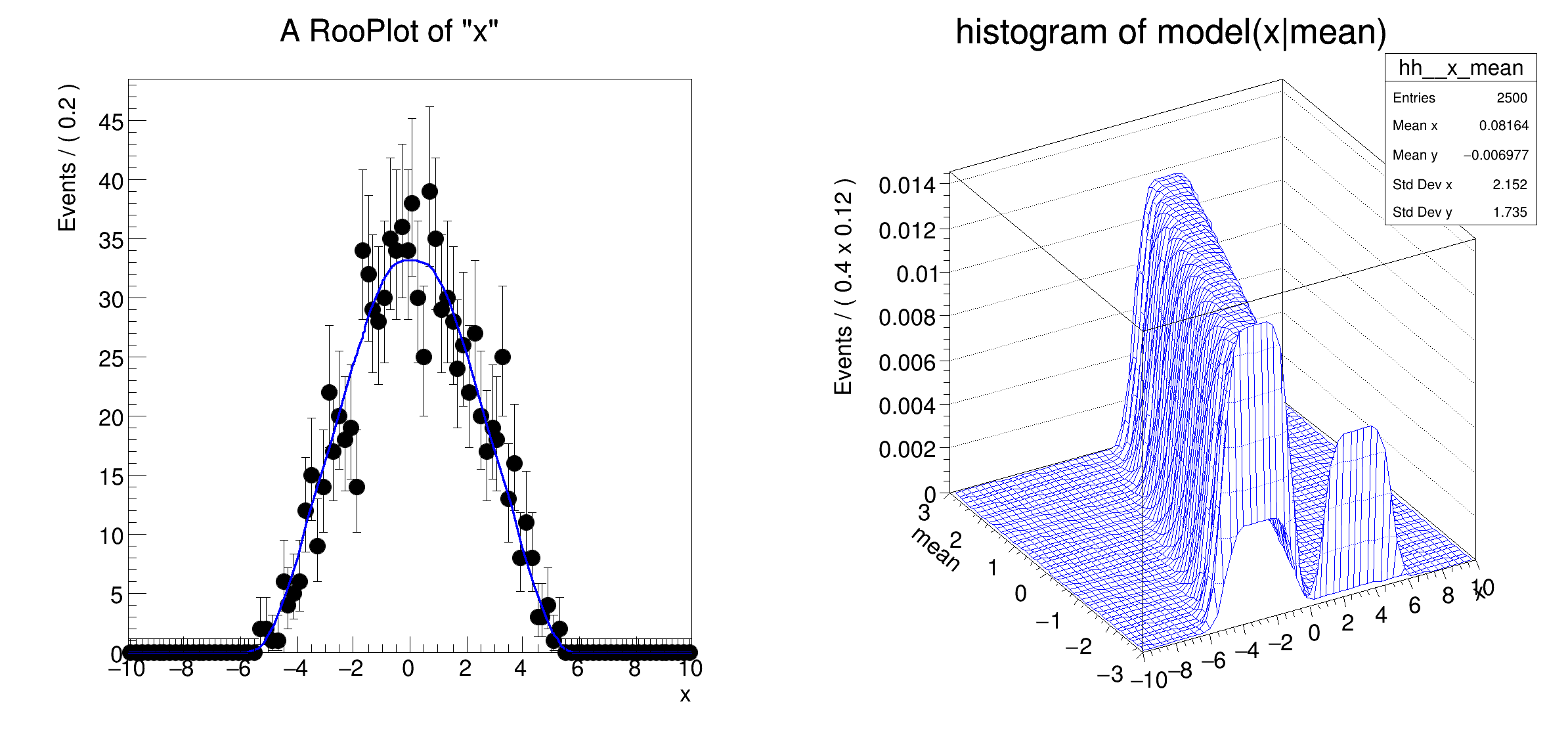
 Addition and convolution: working with a pdf with a convolution operator in terms of a parameter
Addition and convolution: working with a pdf with a convolution operator in terms of a parameter