Namespaces
namespace	multifit

Detailed Description

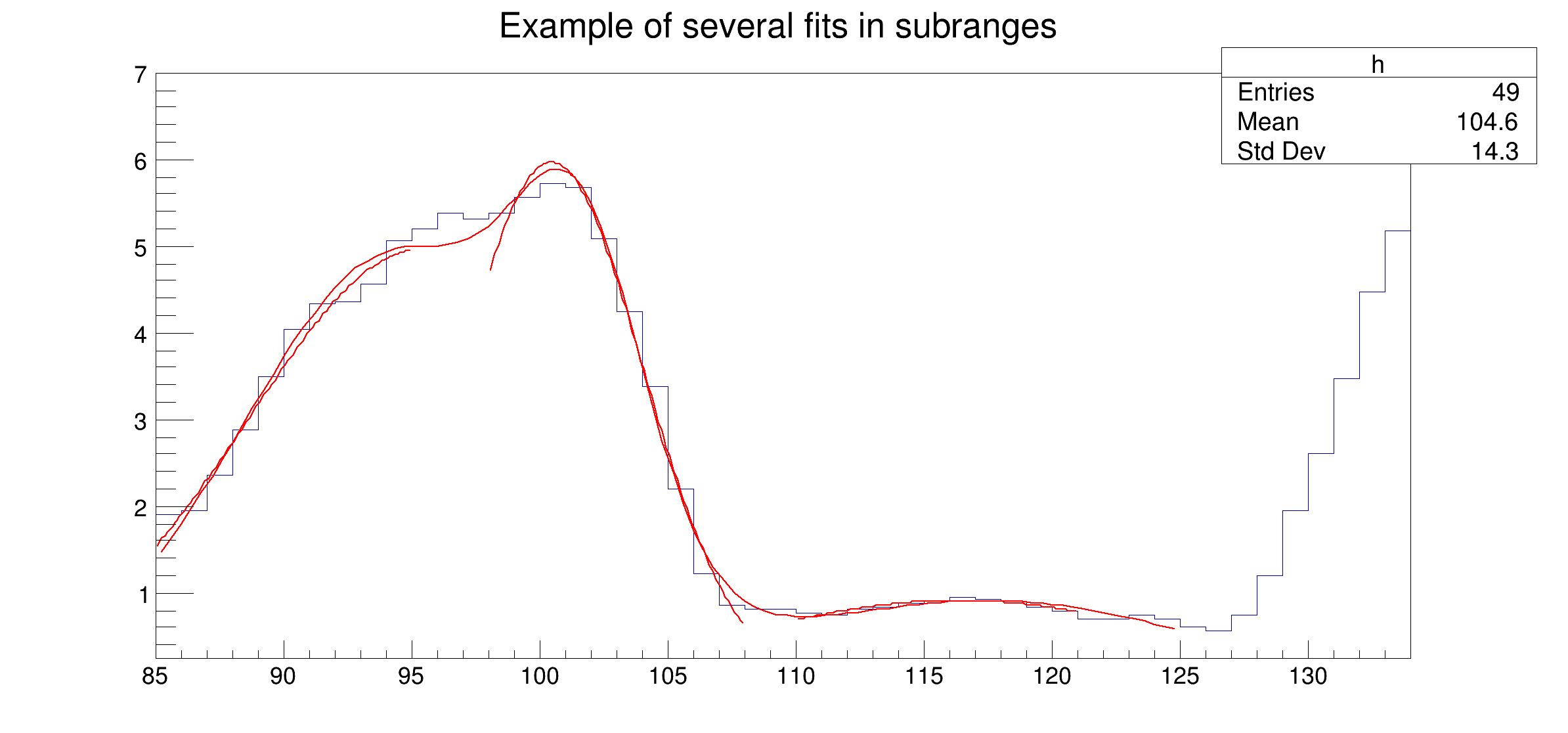
Fitting multiple functions to different ranges of a 1-D histogram Example showing how to fit in a sub-range of an histogram A histogram is created and filled with the bin contents and errors defined in the table below.

Three Gaussians are fitted in sub-ranges of this histogram. A new function (a sum of 3 Gaussians) is fitted on another subrange Note that when fitting simple functions, such as Gaussians, the initial values of parameters are automatically computed by ROOT. In the more complicated case of the sum of 3 Gaussians, the initial values of parameters must be given. In this particular case, the initial values are taken from the result of the individual fits.

 FCN=0.0848003 FROM MIGRAD    STATUS=CONVERGED     105 CALLS         106 TOTAL
                     EDM=1.77382e-07    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     4.96664e+00   2.83221e+00   4.26889e-04   1.67619e-04
   2  Mean         9.54663e+01   1.23905e+01   7.53972e-04  -2.63161e-04
   3  Sigma        6.82779e+00   7.49131e+00   5.87496e-05   3.68521e-03
 FCN=0.0771026 FROM MIGRAD    STATUS=CONVERGED      72 CALLS          73 TOTAL
                     EDM=2.00364e-07    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     5.96312e+00   1.14355e+00   4.82019e-04   1.52951e-04
   2  Mean         1.00467e+02   1.53372e+00   3.74926e-04   6.69980e-04
   3  Sigma        3.54806e+00   1.16899e+00   3.22077e-05   3.86167e-03
 FCN=0.0087702 FROM MIGRAD    STATUS=CONVERGED      93 CALLS          94 TOTAL
                     EDM=5.57239e-07    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     9.12665e-01   4.37176e-01   1.46528e-04   2.91010e-04
   2  Mean         1.16309e+02   8.37408e+00   3.57386e-03  -3.17966e-05
   3  Sigma        8.38413e+00   1.84577e+01   4.99414e-04  -4.98793e-04
 FCN=0.312817 FROM MIGRAD    STATUS=CONVERGED     515 CALLS         516 TOTAL
                     EDM=1.73245e-07    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  p0           4.91145e+00   1.41387e+00   3.61239e-04  -3.22790e-04
   2  p1           9.44525e+01   3.71612e+00   5.60861e-04  -6.78941e-05
   3  p2           5.94796e+00   2.41732e+00   4.25396e-04   2.68176e-05
   4  p3           3.22134e+00   3.11650e+00   5.86729e-04  -1.82620e-04
   5  p4           1.01663e+02   1.67863e+00   5.56527e-04   3.95769e-04
   6  p5           2.48454e+00   1.91461e+00   3.85832e-04   7.23818e-05
   7  p6           9.11463e-01   3.68235e-01   1.45489e-04   5.77239e-04
   8  p7           1.17582e+02   5.06329e+00   2.01798e-03  -8.25382e-05
   9  p8           7.58627e+00   8.76000e+00   2.12468e-03   2.02614e-05
[  4.96663958  95.46632975   6.8277931    5.9631179  100.46745499
   3.54806038   0.91266549 116.30923996   8.38412804]

 
import ROOT
 
import numpy as np
 
n_x = 49
 
# fmt: off
x = np.array( [ 1.913521, 1.953769, 2.347435, 2.883654, 3.493567, 4.047560,
    4.337210, 4.364347, 4.563004, 5.054247, 5.194183, 5.380521, 5.303213,
    5.384578, 5.563983, 5.728500, 5.685752, 5.080029, 4.251809, 3.372246,
    2.207432, 1.227541, 0.8597788, 0.8220503, 0.8046592, 0.7684097, 0.7469761,
    0.8019787, 0.8362375, 0.8744895, 0.9143721, 0.9462768, 0.9285364,
    0.8954604, 0.8410891, 0.7853871, 0.7100883, 0.6938808, 0.7363682,
    0.7032954, 0.6029015, 0.5600163, 0.7477068, 1.188785, 1.938228, 2.602717,
    3.472962, 4.465014, 5.177035, ], dtype=np.float32,)
# fmt: on
 
# The histogram are filled with bins defined in the array x.
h = ROOT.TH1F("h", "Example of several fits in subranges", n_x, 85, 134)
h.SetMaximum(7)
 
for i, x_i in enumerate(x):
    h.SetBinContent(i + 1, x[i])
 
# Define the parameter array for the total function.
par = np.zeros(9)
 
# Three TF1 objects are created, one for each subrange.
g1 = ROOT.TF1("g1", "gaus", 85, 95)
g2 = ROOT.TF1("g2", "gaus", 98, 108)
g3 = ROOT.TF1("g3", "gaus", 110, 121)
 
# The total is the sum of the three, each has three parameters.
total = ROOT.TF1("total", "gaus(0)+gaus(3)+gaus(6)", 85, 125)
total.SetLineColor(2)
 
# The canvas that the histograms and fit functions are drawn on.
c = ROOT.TCanvas("multifit", "multifit", 800, 400)
 
# Fit each function and add it to the list of functions. By default, TH1::Fit()
# fits the function on the defined histogram range. You can specify the "R"
# option in the second parameter of TH1::Fit() to restrict the fit to the range
# specified in the TF1 constructor. Alternatively, you can also specify the
# range in the call to TH1::Fit(), which we demonstrate here with the 3rd
# Gaussian. The "+" option needs to be added to the later fits to not replace
# existing fitted functions in the histogram.
h.Fit(g1, "R")
h.Fit(g2, "R+")
h.Fit(g3, "+", "", 110, 121);
 
# Get the parameters from the fit.
g1.GetParameters(par[:3])
g2.GetParameters(par[3:6])
g3.GetParameters(par[6:])
 
print(par)
 
# Use the parameters on the sum.
total.SetParameters(par)
 
h.Draw()
h.Fit(total, "R+")
 
# Save the plot for later inspection.
c.SaveAs("multifit.png")

Authors: Jonas Rembser, Rene Brun (C++ version)

Definition in file multifit.py.

Namespaces

Detailed Description