rf611_weightedfits.C File Reference

Detailed Description

Likelihood and minimization: Parameter uncertainties for weighted unbinned ML fits

Parameter uncertainties for weighted unbinned ML fits

Based on example from https://arxiv.org/abs/1911.01303

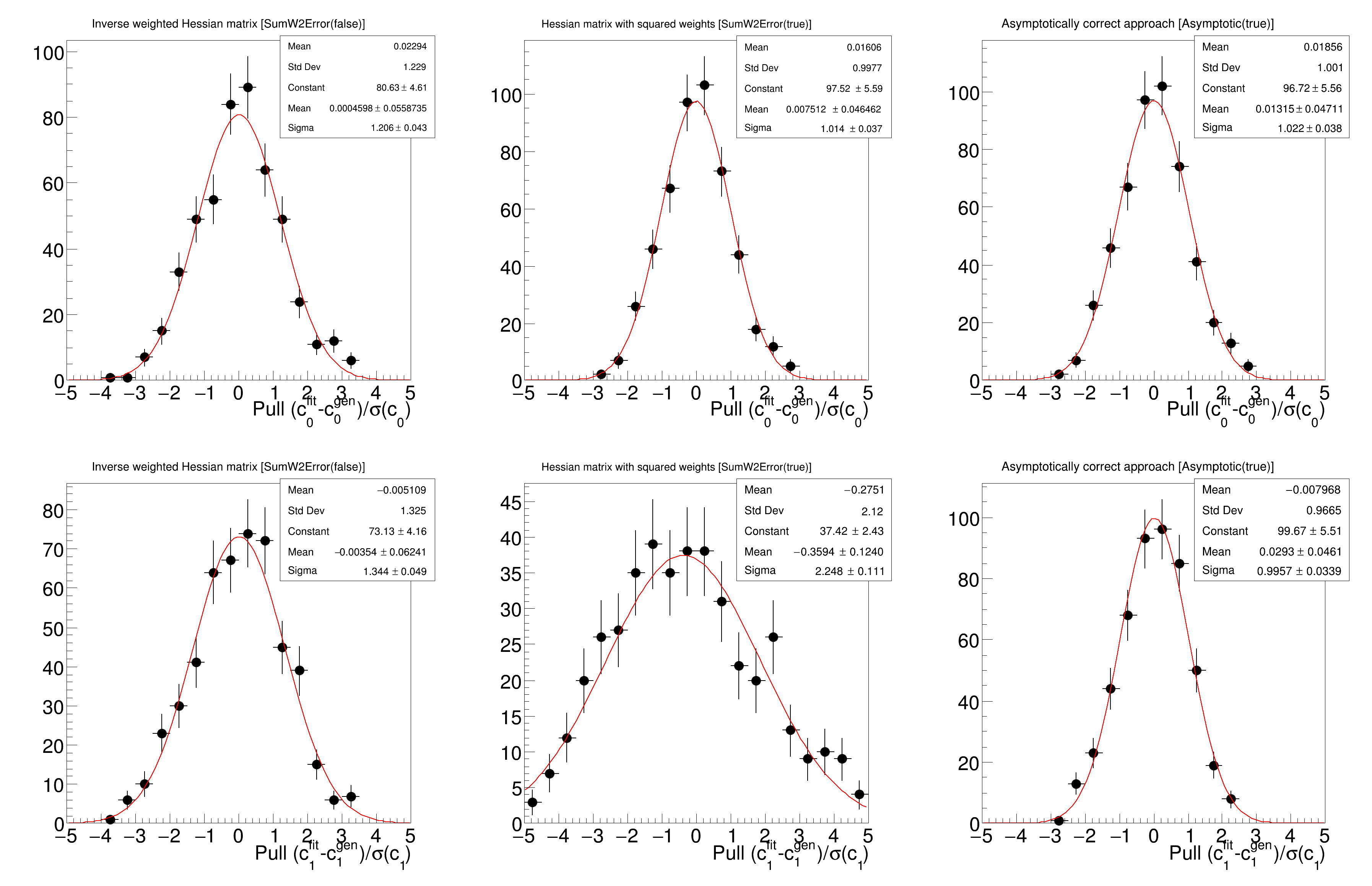
This example compares different approaches to determining parameter uncertainties in weighted unbinned maximum likelihood fits. Performing a weighted unbinned maximum likelihood fits can be useful to account for acceptance effects and to statistically subtract background events using the sPlot formalism. It is however well known that the inverse Hessian matrix does not yield parameter uncertainties with correct coverage in the presence of event weights. Three approaches to the determination of parameter uncertainties are compared in this example:

1. Using the inverse weighted Hessian matrix [SumW2Error(false)]
2. Using the expression [SumW2Error(true)]

   \[ V_{ij} = H_{ik}^{-1} C_{kl} H_{lj}^{-1} \]

   where H is the weighted Hessian matrix and C is the Hessian matrix with squared weights
3. The asymptotically correct approach (for details please see https://arxiv.org/abs/1911.01303) [Asymptotic(true)]

   \[ V_{ij} = H_{ik}^{-1} D_{kl} H_{lj}^{-1} \]

   where H is the weighted Hessian matrix and D is given by

   \[ D_{kl} = \sum_{e=1}^{N} w_e^2 \frac{\partial \log(P)}{\partial \lambda_k}\frac{\partial \log(P)}{\partial \lambda_l} \]

   with the event weight \(w_e\).

The example performs the fit of a second order polynomial in the angle cos(theta) [-1,1] to a weighted data set. The polynomial is given by

\[ P = \frac{ 1 + c_0 \cdot \cos(\theta) + c_1 \cdot \cos(\theta) \cdot \cos(\theta) }{\mathrm{Norm}} \]

The two coefficients \( c_0 \) and \( c_1 \) and their uncertainties are to be determined in the fit.

The per-event weight is used to correct for an acceptance effect, two different acceptance models can be studied:

• acceptancemodel==1: eff = \( 0.3 + 0.7 \cdot \cos(\theta) \cdot \cos(\theta) \)
• acceptancemodel==2: eff = \( 1.0 - 0.7 \cdot \cos(\theta) \cdot \cos(\theta) \) The data is generated to be flat before the acceptance effect.

The performance of the different approaches to determine parameter uncertainties is compared using the pull distributions from a large number of pseudoexperiments. The pull is defined as \( (\lambda_i - \lambda_{gen})/\sigma(\lambda_i) \), where \( \lambda_i \) is the fitted parameter and \( \sigma(\lambda_i) \) its uncertainty for pseudoexperiment number i. If the fit is unbiased and the parameter uncertainties are estimated correctly, the pull distribution should be a Gaussian centered around zero with a width of one.

 
#include "TH1D.h"
#include "TCanvas.h"
#include "TROOT.h"
#include "TStyle.h"
#include "TRandom3.h"
#include "TLegend.h"
#include "RooRealVar.h"
#include "RooFitResult.h"
#include "RooDataSet.h"
#include "RooPolynomial.h"
 
using namespace RooFit;
 
 
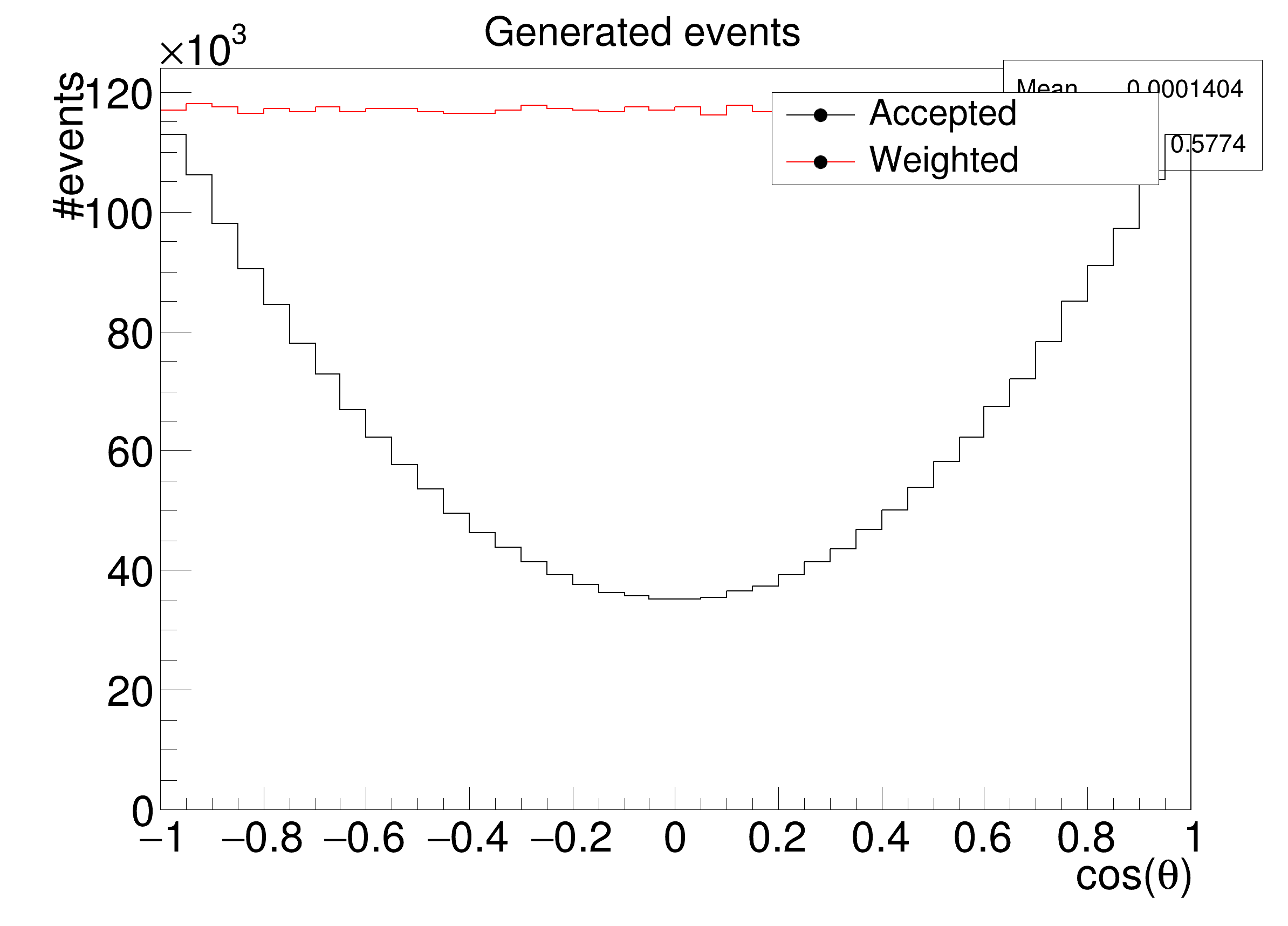
int rf611_weightedfits(int acceptancemodel=2) {
  // I n i t i a l i s a t i o n   a n d   S e t u p
  //------------------------------------------------
 
  //plotting options
  gStyle->SetPaintTextFormat(".1f");
  gStyle->SetEndErrorSize(6.0);
  gStyle->SetTitleSize(0.05, "XY");
  gStyle->SetLabelSize(0.05, "XY");
  gStyle->SetTitleOffset(0.9, "XY");
  gStyle->SetTextSize(0.05);
  gStyle->SetPadLeftMargin(0.125);
  gStyle->SetPadBottomMargin(0.125);
  gStyle->SetPadTopMargin(0.075);
  gStyle->SetPadRightMargin(0.075);
  gStyle->SetMarkerStyle(20);
  gStyle->SetMarkerSize(1.0);
  gStyle->SetHistLineWidth(2.0);
  gStyle->SetHistLineColor(1);
 
  //initialise TRandom3
  TRandom3* rnd = new TRandom3();
  rnd->SetSeed(191101303);
 
  //accepted events and events weighted to account for the acceptance
  TH1D* haccepted = new TH1D("haccepted", "Generated events;cos(#theta);#events", 40, -1.0, 1.0);
  TH1D* hweighted = new TH1D("hweighted", "Generated events;cos(#theta);#events", 40, -1.0, 1.0);
  //histograms holding pull distributions
  //using the inverse Hessian matrix
  TH1D* hc0pull1 = new TH1D("hc0pull1", "Inverse weighted Hessian matrix [SumW2Error(false)];Pull (c_{0}^{fit}-c_{0}^{gen})/#sigma(c_{0});", 20, -5.0, 5.0);
  TH1D* hc1pull1 = new TH1D("hc1pull1", "Inverse weighted Hessian matrix [SumW2Error(false)];Pull (c_{1}^{fit}-c_{1}^{gen})/#sigma(c_{1});", 20, -5.0, 5.0);
  //using the correction with the Hessian matrix with squared weights
  TH1D* hc0pull2 = new TH1D("hc0pull2", "Hessian matrix with squared weights [SumW2Error(true)];Pull (c_{0}^{fit}-c_{0}^{gen})/#sigma(c_{0});", 20, -5.0, 5.0);
  TH1D* hc1pull2 = new TH1D("hc1pull2", "Hessian matrix with squared weights [SumW2Error(true)];Pull (c_{1}^{fit}-c_{1}^{gen})/#sigma(c_{1});", 20, -5.0, 5.0);
  //asymptotically correct approach
  TH1D* hc0pull3 = new TH1D("hc0pull3", "Asymptotically correct approach [Asymptotic(true)];Pull (c_{0}^{fit}-c_{0}^{gen})/#sigma(c_{0});", 20, -5.0, 5.0);
  TH1D* hc1pull3 = new TH1D("hc1pull3", "Asymptotically correct approach [Asymptotic(true)];Pull (c_{1}^{fit}-c_{1}^{gen})/#sigma(c_{1});", 20, -5.0, 5.0);
 
  //number of pseudoexperiments (toys) and number of events per pseudoexperiment
  constexpr unsigned int ntoys = 500;
  constexpr unsigned int nstats = 5000;
  //parameters used in the generation
  constexpr double c0gen = 0.0;
  constexpr double c1gen = 0.0;
 
  // Silence fitting and minimisation messages
  auto& msgSv = RooMsgService::instance();
  msgSv.getStream(1).removeTopic(RooFit::Minimization);
  msgSv.getStream(1).removeTopic(RooFit::Fitting);
 
  std::cout << "Running " << ntoys*3 << " toy fits ..." << std::endl;
 
  // M a i n   l o o p :   r u n   p s e u d o e x p e r i m e n t s
  //----------------------------------------------------------------
  for (unsigned int i=0; i<ntoys; i++) {
    //S e t u p   p a r a m e t e r s   a n d   P D F
    //-----------------------------------------------
    //angle theta and the weight to account for the acceptance effect
    RooRealVar costheta("costheta","costheta", -1.0, 1.0);
    RooRealVar weight("weight","weight", 0.0, 1000.0);
 
    //initialise parameters to fit
    RooRealVar c0("c0","0th-order coefficient", c0gen, -1.0, 1.0);
    RooRealVar c1("c1","1st-order coefficient", c1gen, -1.0, 1.0);
    c0.setError(0.01);
    c1.setError(0.01);
    //create simple second-order polynomial as probability density function
    RooPolynomial pol("pol", "pol", costheta, RooArgList(c0, c1), 1);
 
    //G e n e r a t e   d a t a   s e t   f o r   p s e u d o e x p e r i m e n t   i
    //-------------------------------------------------------------------------------
    RooDataSet data("data","data",RooArgSet(costheta, weight), WeightVar("weight"));
    //generate nstats events
    for (unsigned int j=0; j<nstats; j++) {
      bool finished = false;
      //use simple accept/reject for generation
      while (!finished) {
        costheta = 2.0*rnd->Rndm()-1.0;
        //efficiency for the specific value of cos(theta)
        double eff = 1.0;
        if (acceptancemodel == 1)
          eff = 1.0 - 0.7 * costheta.getVal()*costheta.getVal();
        else
          eff = 0.3 + 0.7 * costheta.getVal()*costheta.getVal();
        //use 1/eff as weight to account for acceptance
        weight = 1.0/eff;
        //accept/reject
        if (10.0*rnd->Rndm() < eff*pol.getVal())
          finished = true;
      }
      haccepted->Fill(costheta.getVal());
      hweighted->Fill(costheta.getVal(), weight.getVal());
      data.add(RooArgSet(costheta, weight), weight.getVal());
    }
 
    //F i t   t o y   u s i n g   t h e   t h r e e   d i f f e r e n t   a p p r o a c h e s   t o   u n c e r t a i n t y   d e t e r m i n a t i o n
    //-------------------------------------------------------------------------------------------------------------------------------------------------
    //this uses the inverse weighted Hessian matrix
    std::unique_ptr<RooFitResult> result{pol.fitTo(data, Save(true), SumW2Error(false), PrintLevel(-1), BatchMode(true))};
    hc0pull1->Fill((c0.getVal()-c0gen)/c0.getError());
    hc1pull1->Fill((c1.getVal()-c1gen)/c1.getError());
 
    //this uses the correction with the Hesse matrix with squared weights
    result = std::unique_ptr<RooFitResult>{pol.fitTo(data, Save(true), SumW2Error(true), PrintLevel(-1), BatchMode(true))};
    hc0pull2->Fill((c0.getVal()-c0gen)/c0.getError());
    hc1pull2->Fill((c1.getVal()-c1gen)/c1.getError());
 
    //this uses the asymptotically correct approach
    result = std::unique_ptr<RooFitResult>{pol.fitTo(data, Save(true), AsymptoticError(true), PrintLevel(-1), BatchMode(true))};
    hc0pull3->Fill((c0.getVal()-c0gen)/c0.getError());
    hc1pull3->Fill((c1.getVal()-c1gen)/c1.getError());
  }
 
  std::cout << "... done." << std::endl;
 
  // P l o t   o u t p u t   d i s t r i b u t i o n s
  //--------------------------------------------------
 
  //plot accepted (weighted) events
  gStyle->SetOptStat(0);
  gStyle->SetOptFit(0);
  TCanvas* cevents = new TCanvas("cevents", "cevents", 800, 600);
  cevents->cd(1);
  hweighted->SetMinimum(0.0);
  hweighted->SetLineColor(2);
  hweighted->Draw("hist");
  haccepted->Draw("same hist");
  TLegend* leg = new TLegend(0.6, 0.8, 0.9, 0.9);
  leg->AddEntry(haccepted, "Accepted");
  leg->AddEntry(hweighted, "Weighted");
  leg->Draw();
  cevents->Update();
 
  //plot pull distributions
  TCanvas* cpull = new TCanvas("cpull", "cpull", 1200, 800);
  cpull->Divide(3,2);
  cpull->cd(1);
  gStyle->SetOptStat(1100);
  gStyle->SetOptFit(11);
  hc0pull1->Fit("gaus");
  hc0pull1->Draw("ep");
  cpull->cd(2);
  hc0pull2->Fit("gaus");
  hc0pull2->Draw("ep");
  cpull->cd(3);
  hc0pull3->Fit("gaus");
  hc0pull3->Draw("ep");
  cpull->cd(4);
  hc1pull1->Fit("gaus");
  hc1pull1->Draw("ep");
  cpull->cd(5);
  hc1pull2->Fit("gaus");
  hc1pull2->Draw("ep");
  cpull->cd(6);
  hc1pull3->Fit("gaus");
  hc1pull3->Draw("ep");
  cpull->Update();
 
  return 0;
}

 
Running 1500 toy fits ...
... done.
 FCN=13.515 FROM MIGRAD    STATUS=CONVERGED      60 CALLS          61 TOTAL
                     EDM=7.11482e-10    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     8.06326e+01   4.61035e+00   6.80051e-03   2.63179e-06
   2  Mean         4.59821e-04   5.58735e-02   1.02835e-04  -6.59629e-04
   3  Sigma        1.20608e+00   4.29699e-02   1.71309e-05   1.24617e-03
 FCN=5.84356 FROM MIGRAD    STATUS=CONVERGED      59 CALLS          60 TOTAL
                     EDM=4.43987e-09    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     9.75213e+01   5.59338e+00   5.60402e-03  -1.97617e-05
   2  Mean         7.51216e-03   4.64617e-02   5.90804e-05  -7.04981e-04
   3  Sigma        1.01358e+00   3.70947e-02   1.21766e-05  -6.78934e-03
 FCN=5.92321 FROM MIGRAD    STATUS=CONVERGED      59 CALLS          60 TOTAL
                     EDM=2.82374e-09    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     9.67219e+01   5.56424e+00   5.59080e-03  -1.59410e-05
   2  Mean         1.31546e-02   4.71082e-02   5.99842e-05  -5.99126e-04
   3  Sigma        1.02204e+00   3.77681e-02   1.23082e-05  -4.76847e-03
 FCN=9.99353 FROM MIGRAD    STATUS=CONVERGED      51 CALLS          52 TOTAL
                     EDM=1.54209e-08    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     7.31330e+01   4.15612e+00   5.34878e-03   8.14696e-06
   2  Mean        -3.53982e-03   6.24075e-02   1.00776e-04   2.69686e-03
   3  Sigma        1.34426e+00   4.86401e-02   1.55414e-05   6.26797e-03
 FCN=13.9377 FROM MIGRAD    STATUS=CONVERGED      59 CALLS          60 TOTAL
                     EDM=1.41305e-07    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     3.74207e+01   2.42528e+00   3.48790e-03  -5.82511e-05
   2  Mean        -3.59360e-01   1.24029e-01   2.28239e-04   3.37657e-03
   3  Sigma        2.24823e+00   1.11069e-01   2.42149e-05  -2.95187e-02
 FCN=6.06878 FROM MIGRAD    STATUS=CONVERGED      60 CALLS          61 TOTAL
                     EDM=2.14707e-09    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     9.96656e+01   5.51125e+00   5.82217e-03  -7.19806e-06
   2  Mean         2.92964e-02   4.61022e-02   5.98483e-05   1.20218e-03
   3  Sigma        9.95652e-01   3.38750e-02   1.20391e-05  -3.38248e-03
(int) 0

Date

November 2019

Author

Christoph Langenbruch

Definition in file rf611_weightedfits.C.