rs101_limitexample.py File Reference

Namespaces
namespace	rs101_limitexample

Detailed Description

Limits: number counting experiment with uncertainty on both the background rate and signal efficiency.

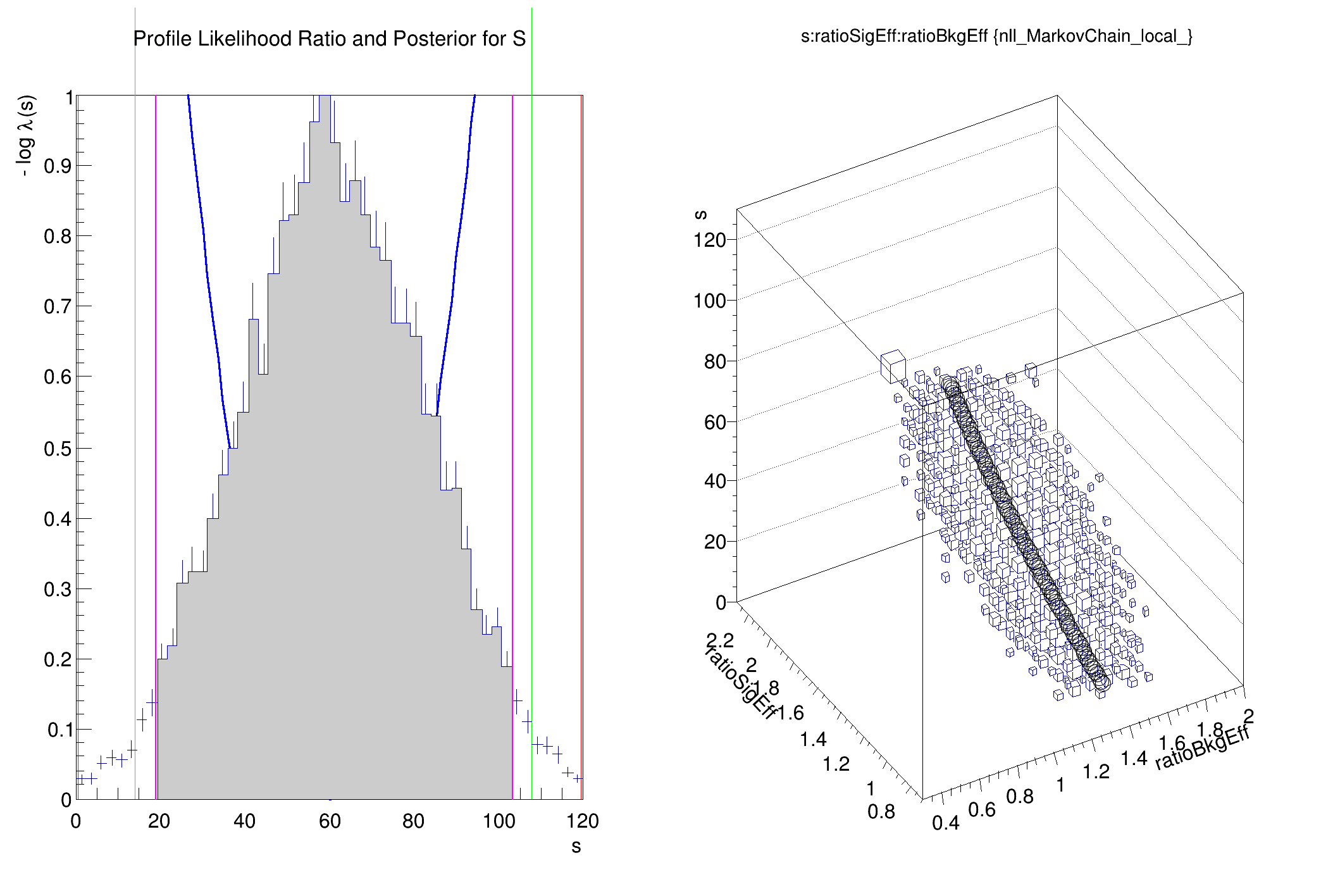
The usage of a Confidence Interval Calculator to set a limit on the signal is illustrated

 
RooWorkspace()  contents
 
variables
---------
(b,gSigBkg,gSigEff,obs,ratioBkgEff,ratioSigEff,s)
 
p.d.f.s
-------
RooGaussian::bkgConstraint[ x=gSigBkg mean=ratioBkgEff sigma=0.2 ] = 1
RooPoisson::countingModel[ x=obs mean=countingModel_2 ] = 0.0325554
RooProdPdf::modelWithConstraints[ countingModel * sigConstraint * bkgConstraint ] = 0.0325554
RooGaussian::sigConstraint[ x=gSigEff mean=ratioSigEff sigma=0.05 ] = 1
 
functions
--------
RooAddition::countingModel_2[ countingModel_2_[s_x_ratioSigEff] + countingModel_2_[b_x_ratioBkgEff] ] = 150
RooProduct::countingModel_2_[b_x_ratioBkgEff][ b * ratioBkgEff ] = 100
RooProduct::countingModel_2_[s_x_ratioSigEff][ s * ratioSigEff ] = 50
 
[#1] INFO:Minimization --  Including the following constraint terms in minimization: (sigConstraint,bkgConstraint)
[#1] INFO:Minimization -- The global observables are not defined , normalize constraints with respect to the parameters (ratioSigEff,ratioBkgEff)
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_modelWithConstraints_exampleData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization --  The following expressions will be evaluated in cache-and-track mode: (countingModel)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:ObjectHandling -- RooWorkspace::import() importing dataset exampleData
[#1] INFO:InputArguments -- The deprecated RooFit::CloneData(1) option passed to createNLL() is ignored.
[#1] INFO:Minimization --  Including the following constraint terms in minimization: (sigConstraint,bkgConstraint)
[#1] INFO:Minimization -- The following global observables have been defined and their values are taken from the model: (gSigEff,gSigBkg)
[#0] PROGRESS:Minimization -- ProfileLikelihoodCalcultor::DoGLobalFit - find MLE 
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_modelWithConstraints_exampleData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization --  The following expressions will be evaluated in cache-and-track mode: (countingModel)
[#0] PROGRESS:Minimization -- ProfileLikelihoodCalcultor::DoMinimizeNLL - using Minuit / Migrad with strategy 1
[#1] INFO:Minimization -- 
  RooFitResult: minimized FCN value: 0.689753, estimated distance to minimum: 9.56453e-09
                covariance matrix quality: Full, accurate covariance matrix
                Status : MINIMIZE=0 
 
    Floating Parameter    FinalValue +/-  Error   
  --------------------  --------------------------
           ratioBkgEff    1.0000e+00 +/-  1.99e-01
           ratioSigEff    1.0000e+00 +/-  5.00e-02
                     s    5.9998e+01 +/-  2.32e+01
 
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) Creating instance of MINUIT
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_modelWithConstraints_exampleData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) determining minimum likelihood for current configurations w.r.t all observable
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) minimum found at (s=59.9982)
.
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) Creating instance of MINUIT
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_modelWithConstraints_exampleData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) determining minimum likelihood for current configurations w.r.t all observable
[#0] ERROR:InputArguments -- RooArgSet::checkForDup: ERROR argument with name s is already in this set
[#1] INFO:Minimization -- RooProfileLL::evaluate(nll_modelWithConstraints_exampleData_with_constr_Profile[s]) minimum found at (s=59.9989)
..........................................................................................................................................................................................................
=== Using the following for ModelConfig ===
Observables:             RooArgSet:: = (obs)
Parameters of Interest:  RooArgSet:: = (s)
Nuisance Parameters:     RooArgSet:: = (ratioSigEff,ratioBkgEff)
Global Observables:      RooArgSet:: = (gSigEff,gSigBkg)
PDF:                     RooProdPdf::modelWithConstraints[ countingModel * sigConstraint * bkgConstraint ] = 0.00460195
 
FeldmanCousins: ntoys per point: adaptive
FeldmanCousins: nEvents per toy will not fluctuate, will always be 1
FeldmanCousins: Model has nuisance parameters, will do profile construction
FeldmanCousins: # points to test = 100
NeymanConstruction: Prog: 1/100 total MC = 80 this test stat = 3.21178
 s=0.6 ratioSigEff=0.999976 ratioBkgEff=1.43644 [-1e+30, 4.68588]  in interval = 1
 
NeymanConstruction: Prog: 2/100 total MC = 80 this test stat = 3.08218
 s=1.8 ratioSigEff=1.00018 ratioBkgEff=1.42695 [-1e+30, 3.71884]  in interval = 1
 
NeymanConstruction: Prog: 3/100 total MC = 80 this test stat = 2.95515
 s=3 ratioSigEff=1.00055 ratioBkgEff=1.4177 [-1e+30, 3.91238]  in interval = 1
 
NeymanConstruction: Prog: 4/100 total MC = 80 this test stat = 2.83091
 s=4.2 ratioSigEff=1.00106 ratioBkgEff=1.40849 [-1e+30, 3.65945]  in interval = 1
 
NeymanConstruction: Prog: 5/100 total MC = 80 this test stat = 2.7093
 s=5.4 ratioSigEff=1.00133 ratioBkgEff=1.39955 [-1e+30, 3.10318]  in interval = 1
 
NeymanConstruction: Prog: 6/100 total MC = 80 this test stat = 2.59036
 s=6.6 ratioSigEff=1.00159 ratioBkgEff=1.39061 [-1e+30, 2.97611]  in interval = 1
 
NeymanConstruction: Prog: 7/100 total MC = 240 this test stat = 2.47407
 s=7.8 ratioSigEff=1.00186 ratioBkgEff=1.38228 [-1e+30, 3.15094]  in interval = 1
 
NeymanConstruction: Prog: 8/100 total MC = 80 this test stat = 2.36054
 s=9 ratioSigEff=1.0021 ratioBkgEff=1.37325 [-1e+30, 3.1239]  in interval = 1
 
NeymanConstruction: Prog: 9/100 total MC = 80 this test stat = 2.24968
 s=10.2 ratioSigEff=1.00232 ratioBkgEff=1.36423 [-1e+30, 3.40684]  in interval = 1
 
NeymanConstruction: Prog: 10/100 total MC = 80 this test stat = 2.14147
 s=11.4 ratioSigEff=1.00253 ratioBkgEff=1.35522 [-1e+30, 3.1714]  in interval = 1
 
NeymanConstruction: Prog: 11/100 total MC = 80 this test stat = 2.03601
 s=12.6 ratioSigEff=1.00268 ratioBkgEff=1.3462 [-1e+30, 3.24645]  in interval = 1
 
NeymanConstruction: Prog: 12/100 total MC = 80 this test stat = 1.93321
 s=13.8 ratioSigEff=1.00287 ratioBkgEff=1.3372 [-1e+30, 2.53824]  in interval = 1
 
NeymanConstruction: Prog: 13/100 total MC = 80 this test stat = 1.83309
 s=15 ratioSigEff=1.00308 ratioBkgEff=1.32821 [-1e+30, 2.70016]  in interval = 1
 
NeymanConstruction: Prog: 14/100 total MC = 80 this test stat = 1.73564
 s=16.2 ratioSigEff=1.00323 ratioBkgEff=1.31922 [-1e+30, 2.77008]  in interval = 1
 
NeymanConstruction: Prog: 15/100 total MC = 80 this test stat = 1.64094
 s=17.4 ratioSigEff=1.00337 ratioBkgEff=1.31025 [-1e+30, 2.84065]  in interval = 1
 
NeymanConstruction: Prog: 16/100 total MC = 80 this test stat = 1.5489
 s=18.6 ratioSigEff=1.00347 ratioBkgEff=1.30119 [-1e+30, 2.44334]  in interval = 1
 
NeymanConstruction: Prog: 17/100 total MC = 80 this test stat = 1.4595
 s=19.8 ratioSigEff=1.00359 ratioBkgEff=1.29224 [-1e+30, 2.51006]  in interval = 1
 
NeymanConstruction: Prog: 18/100 total MC = 80 this test stat = 1.37287
 s=21 ratioSigEff=1.0037 ratioBkgEff=1.2833 [-1e+30, 2.30853]  in interval = 1
 
NeymanConstruction: Prog: 19/100 total MC = 80 this test stat = 1.28887
 s=22.2 ratioSigEff=1.00379 ratioBkgEff=1.27438 [-1e+30, 2.11523]  in interval = 1
 
NeymanConstruction: Prog: 20/100 total MC = 80 this test stat = 1.20756
 s=23.4 ratioSigEff=1.00387 ratioBkgEff=1.26546 [-1e+30, 2.09374]  in interval = 1
 
NeymanConstruction: Prog: 21/100 total MC = 80 this test stat = 1.12892
 s=24.6 ratioSigEff=1.00394 ratioBkgEff=1.25655 [-1e+30, 2.1559]  in interval = 1
 
NeymanConstruction: Prog: 22/100 total MC = 80 this test stat = 1.05299
 s=25.8 ratioSigEff=1.00399 ratioBkgEff=1.24765 [-1e+30, 2.48172]  in interval = 1
 
NeymanConstruction: Prog: 23/100 total MC = 80 this test stat = 0.979748
 s=27 ratioSigEff=1.00403 ratioBkgEff=1.23877 [-1e+30, 1.9489]  in interval = 1
 
NeymanConstruction: Prog: 24/100 total MC = 80 this test stat = 0.909174
 s=28.2 ratioSigEff=1.00405 ratioBkgEff=1.22989 [-1e+30, 1.92837]  in interval = 1
 
NeymanConstruction: Prog: 25/100 total MC = 80 this test stat = 0.841264
 s=29.4 ratioSigEff=1.00408 ratioBkgEff=1.22097 [-1e+30, 1.90797]  in interval = 1
 
NeymanConstruction: Prog: 26/100 total MC = 80 this test stat = 0.776027
 s=30.6 ratioSigEff=1.00408 ratioBkgEff=1.21214 [-1e+30, 2.04836]  in interval = 1
 
NeymanConstruction: Prog: 27/100 total MC = 80 this test stat = 0.713453
 s=31.8 ratioSigEff=1.00406 ratioBkgEff=1.2033 [-1e+30, 1.42563]  in interval = 1
 
NeymanConstruction: Prog: 28/100 total MC = 80 this test stat = 0.653543
 s=33 ratioSigEff=1.00403 ratioBkgEff=1.19446 [-1e+30, 1.92614]  in interval = 1
 
NeymanConstruction: Prog: 29/100 total MC = 80 this test stat = 0.596293
 s=34.2 ratioSigEff=1.00399 ratioBkgEff=1.18562 [-1e+30, 1.53064]  in interval = 1
 
NeymanConstruction: Prog: 30/100 total MC = 80 this test stat = 0.541678
 s=35.4 ratioSigEff=1.00393 ratioBkgEff=1.17679 [-1e+30, 1.65725]  in interval = 1
 
NeymanConstruction: Prog: 31/100 total MC = 80 this test stat = 0.489749
 s=36.6 ratioSigEff=1.00386 ratioBkgEff=1.16795 [-1e+30, 1.42567]  in interval = 1
 
NeymanConstruction: Prog: 32/100 total MC = 80 this test stat = 0.440465
 s=37.8 ratioSigEff=1.00378 ratioBkgEff=1.15913 [-1e+30, 1.40855]  in interval = 1
 
NeymanConstruction: Prog: 33/100 total MC = 80 this test stat = 0.393811
 s=39 ratioSigEff=1.00369 ratioBkgEff=1.15032 [-1e+30, 1.2593]  in interval = 1
 
NeymanConstruction: Prog: 34/100 total MC = 80 this test stat = 0.349798
 s=40.2 ratioSigEff=1.00358 ratioBkgEff=1.14152 [-1e+30, 1.30825]  in interval = 1
 
NeymanConstruction: Prog: 35/100 total MC = 80 this test stat = 0.30842
 s=41.4 ratioSigEff=1.00347 ratioBkgEff=1.13274 [-1e+30, 0.874179]  in interval = 1
 
NeymanConstruction: Prog: 36/100 total MC = 80 this test stat = 0.269673
 s=42.6 ratioSigEff=1.00334 ratioBkgEff=1.12397 [-1e+30, 1.14949]  in interval = 1
 
NeymanConstruction: Prog: 37/100 total MC = 80 this test stat = 0.233551
 s=43.8 ratioSigEff=1.00319 ratioBkgEff=1.11573 [-1e+30, 1.07403]  in interval = 1
 
NeymanConstruction: Prog: 38/100 total MC = 80 this test stat = 0.200042
 s=45 ratioSigEff=1.00303 ratioBkgEff=1.10705 [-1e+30, 1.30848]  in interval = 1
 
NeymanConstruction: Prog: 39/100 total MC = 80 this test stat = 0.169154
 s=46.2 ratioSigEff=1.00285 ratioBkgEff=1.09838 [-1e+30, 0.987229]  in interval = 1
 
NeymanConstruction: Prog: 40/100 total MC = 80 this test stat = 0.140928
 s=47.4 ratioSigEff=1.00267 ratioBkgEff=1.08972 [-1e+30, 0.917557]  in interval = 1
 
NeymanConstruction: Prog: 41/100 total MC = 80 this test stat = 0.115258
 s=48.6 ratioSigEff=1.00247 ratioBkgEff=1.08109 [-1e+30, 0.850481]  in interval = 1
 
NeymanConstruction: Prog: 42/100 total MC = 80 this test stat = 0.0921856
 s=49.8 ratioSigEff=1.00226 ratioBkgEff=1.07247 [-1e+30, 0.891152]  in interval = 1
 
NeymanConstruction: Prog: 43/100 total MC = 80 this test stat = 0.071704
 s=51 ratioSigEff=1.00204 ratioBkgEff=1.06387 [-1e+30, 1.04631]  in interval = 1
 
NeymanConstruction: Prog: 44/100 total MC = 80 this test stat = 0.0538069
 s=52.2 ratioSigEff=1.00181 ratioBkgEff=1.05529 [-1e+30, 0.574131]  in interval = 1
 
NeymanConstruction: Prog: 45/100 total MC = 80 this test stat = 0.0384876
 s=53.4 ratioSigEff=1.00156 ratioBkgEff=1.04672 [-1e+30, 0.749926]  in interval = 1
 
NeymanConstruction: Prog: 46/100 total MC = 80 this test stat = 0.0257395
 s=54.6 ratioSigEff=1.00131 ratioBkgEff=1.03818 [-1e+30, 0.839739]  in interval = 1
 
NeymanConstruction: Prog: 47/100 total MC = 80 this test stat = 0.0155555
 s=55.8 ratioSigEff=1.00104 ratioBkgEff=1.02966 [-1e+30, 0.715161]  in interval = 1
 
NeymanConstruction: Prog: 48/100 total MC = 80 this test stat = 0.00792855
 s=57 ratioSigEff=1.00075 ratioBkgEff=1.02116 [-1e+30, 0.574145]  in interval = 1
 
NeymanConstruction: Prog: 49/100 total MC = 80 this test stat = 0.00285134
 s=58.2 ratioSigEff=1.00046 ratioBkgEff=1.01268 [-1e+30, 0.732099]  in interval = 1
 
NeymanConstruction: Prog: 50/100 total MC = 80 this test stat = 0.000340162
 s=59.4 ratioSigEff=1.00051 ratioBkgEff=1.00385 [-1e+30, 0.692058]  in interval = 1
 
NeymanConstruction: Prog: 51/100 total MC = 80 this test stat = 0.000338383
 s=60.6 ratioSigEff=0.999538 ratioBkgEff=0.996051 [-1e+30, 0.645986]  in interval = 1
 
NeymanConstruction: Prog: 52/100 total MC = 80 this test stat = 0.00280022
 s=61.8 ratioSigEff=0.999513 ratioBkgEff=0.987372 [-1e+30, 0.513396]  in interval = 1
 
NeymanConstruction: Prog: 53/100 total MC = 80 this test stat = 0.00784733
 s=63 ratioSigEff=0.999173 ratioBkgEff=0.978981 [-1e+30, 0.477501]  in interval = 1
 
NeymanConstruction: Prog: 54/100 total MC = 80 this test stat = 0.0154172
 s=64.2 ratioSigEff=0.998823 ratioBkgEff=0.970615 [-1e+30, 0.721505]  in interval = 1
 
NeymanConstruction: Prog: 55/100 total MC = 80 this test stat = 0.0254769
 s=65.4 ratioSigEff=0.998461 ratioBkgEff=0.962272 [-1e+30, 0.628705]  in interval = 1
 
NeymanConstruction: Prog: 56/100 total MC = 80 this test stat = 0.0380399
 s=66.6 ratioSigEff=0.998088 ratioBkgEff=0.953953 [-1e+30, 0.636603]  in interval = 1
 
NeymanConstruction: Prog: 57/100 total MC = 80 this test stat = 0.0530874
 s=67.8 ratioSigEff=0.997703 ratioBkgEff=0.945659 [-1e+30, 0.596425]  in interval = 1
 
NeymanConstruction: Prog: 58/100 total MC = 80 this test stat = 0.0706058
 s=69 ratioSigEff=0.997308 ratioBkgEff=0.93739 [-1e+30, 0.865376]  in interval = 1
 
NeymanConstruction: Prog: 59/100 total MC = 80 this test stat = 0.0905894
 s=70.2 ratioSigEff=0.996902 ratioBkgEff=0.929146 [-1e+30, 0.817861]  in interval = 1
 
NeymanConstruction: Prog: 60/100 total MC = 80 this test stat = 0.11303
 s=71.4 ratioSigEff=0.996485 ratioBkgEff=0.920928 [-1e+30, 1.06483]  in interval = 1
 
NeymanConstruction: Prog: 61/100 total MC = 80 this test stat = 0.137918
 s=72.6 ratioSigEff=0.996057 ratioBkgEff=0.912736 [-1e+30, 0.780337]  in interval = 1
 
NeymanConstruction: Prog: 62/100 total MC = 80 this test stat = 0.165246
 s=73.8 ratioSigEff=0.995619 ratioBkgEff=0.904571 [-1e+30, 0.684448]  in interval = 1
 
NeymanConstruction: Prog: 63/100 total MC = 80 this test stat = 0.195001
 s=75 ratioSigEff=0.99517 ratioBkgEff=0.896432 [-1e+30, 1.03028]  in interval = 1
 
NeymanConstruction: Prog: 64/100 total MC = 80 this test stat = 0.227176
 s=76.2 ratioSigEff=0.99471 ratioBkgEff=0.888321 [-1e+30, 0.978198]  in interval = 1
 
NeymanConstruction: Prog: 65/100 total MC = 80 this test stat = 0.261776
 s=77.4 ratioSigEff=0.99424 ratioBkgEff=0.880238 [-1e+30, 1.11253]  in interval = 1
 
NeymanConstruction: Prog: 66/100 total MC = 80 this test stat = 0.298772
 s=78.6 ratioSigEff=0.99376 ratioBkgEff=0.872182 [-1e+30, 1.1878]  in interval = 1
 
NeymanConstruction: Prog: 67/100 total MC = 80 this test stat = 0.338144
 s=79.8 ratioSigEff=0.993269 ratioBkgEff=0.864155 [-1e+30, 1.48097]  in interval = 1
 
NeymanConstruction: Prog: 68/100 total MC = 80 this test stat = 0.379914
 s=81 ratioSigEff=0.992768 ratioBkgEff=0.856156 [-1e+30, 1.56743]  in interval = 1
 
NeymanConstruction: Prog: 69/100 total MC = 80 this test stat = 0.424071
 s=82.2 ratioSigEff=0.992257 ratioBkgEff=0.848186 [-1e+30, 1.28528]  in interval = 1
 
NeymanConstruction: Prog: 70/100 total MC = 80 this test stat = 0.470561
 s=83.4 ratioSigEff=0.991736 ratioBkgEff=0.840246 [-1e+30, 1.43791]  in interval = 1
 
NeymanConstruction: Prog: 71/100 total MC = 80 this test stat = 0.519388
 s=84.6 ratioSigEff=0.991205 ratioBkgEff=0.832335 [-1e+30, 1.84071]  in interval = 1
 
NeymanConstruction: Prog: 72/100 total MC = 80 this test stat = 0.570629
 s=85.8 ratioSigEff=0.990664 ratioBkgEff=0.824454 [-1e+30, 1.31507]  in interval = 1
 
NeymanConstruction: Prog: 73/100 total MC = 80 this test stat = 0.624119
 s=87 ratioSigEff=0.990114 ratioBkgEff=0.816603 [-1e+30, 1.18907]  in interval = 1
 
NeymanConstruction: Prog: 74/100 total MC = 80 this test stat = 0.679954
 s=88.2 ratioSigEff=0.989553 ratioBkgEff=0.808783 [-1e+30, 1.33487]  in interval = 1
 
NeymanConstruction: Prog: 75/100 total MC = 80 this test stat = 0.738064
 s=89.4 ratioSigEff=0.988831 ratioBkgEff=0.800144 [-1e+30, 1.56433]  in interval = 1
 
NeymanConstruction: Prog: 76/100 total MC = 80 this test stat = 0.798499
 s=90.6 ratioSigEff=0.988237 ratioBkgEff=0.792303 [-1e+30, 1.49944]  in interval = 1
 
NeymanConstruction: Prog: 77/100 total MC = 80 this test stat = 0.861245
 s=91.8 ratioSigEff=0.987632 ratioBkgEff=0.784488 [-1e+30, 1.7418]  in interval = 1
 
NeymanConstruction: Prog: 78/100 total MC = 80 this test stat = 0.926247
 s=93 ratioSigEff=0.987017 ratioBkgEff=0.7767 [-1e+30, 1.37459]  in interval = 1
 
NeymanConstruction: Prog: 79/100 total MC = 80 this test stat = 0.993496
 s=94.2 ratioSigEff=0.986393 ratioBkgEff=0.76894 [-1e+30, 2.1909]  in interval = 1
 
NeymanConstruction: Prog: 80/100 total MC = 80 this test stat = 1.06297
 s=95.4 ratioSigEff=0.985758 ratioBkgEff=0.761207 [-1e+30, 1.85545]  in interval = 1
 
NeymanConstruction: Prog: 81/100 total MC = 80 this test stat = 1.13473
 s=96.6 ratioSigEff=0.985113 ratioBkgEff=0.753502 [-1e+30, 1.86619]  in interval = 1
 
NeymanConstruction: Prog: 82/100 total MC = 80 this test stat = 1.20872
 s=97.8 ratioSigEff=0.984458 ratioBkgEff=0.745825 [-1e+30, 2.41018]  in interval = 1
 
NeymanConstruction: Prog: 83/100 total MC = 80 this test stat = 1.28491
 s=99 ratioSigEff=0.983794 ratioBkgEff=0.738176 [-1e+30, 2.4215]  in interval = 1
 
NeymanConstruction: Prog: 84/100 total MC = 80 this test stat = 1.36329
 s=100.2 ratioSigEff=0.98312 ratioBkgEff=0.730555 [-1e+30, 2.43281]  in interval = 1
 
NeymanConstruction: Prog: 85/100 total MC = 80 this test stat = 1.44387
 s=101.4 ratioSigEff=0.982436 ratioBkgEff=0.722963 [-1e+30, 2.44404]  in interval = 1
 
NeymanConstruction: Prog: 86/100 total MC = 80 this test stat = 1.52662
 s=102.6 ratioSigEff=0.981742 ratioBkgEff=0.7154 [-1e+30, 2.09032]  in interval = 1
 
NeymanConstruction: Prog: 87/100 total MC = 80 this test stat = 1.61153
 s=103.8 ratioSigEff=0.981039 ratioBkgEff=0.707866 [-1e+30, 2.76135]  in interval = 1
 
NeymanConstruction: Prog: 88/100 total MC = 80 this test stat = 1.69863
 s=105 ratioSigEff=0.980326 ratioBkgEff=0.700361 [-1e+30, 2.20046]  in interval = 1
 
NeymanConstruction: Prog: 89/100 total MC = 80 this test stat = 1.78786
 s=106.2 ratioSigEff=0.979605 ratioBkgEff=0.692886 [-1e+30, 2.58534]  in interval = 1
 
NeymanConstruction: Prog: 90/100 total MC = 80 this test stat = 1.87921
 s=107.4 ratioSigEff=0.978873 ratioBkgEff=0.685441 [-1e+30, 2.89797]  in interval = 1
 
NeymanConstruction: Prog: 91/100 total MC = 80 this test stat = 1.97265
 s=108.6 ratioSigEff=0.978133 ratioBkgEff=0.678026 [-1e+30, 3.1204]  in interval = 1
 
NeymanConstruction: Prog: 92/100 total MC = 80 this test stat = 2.06825
 s=109.8 ratioSigEff=0.977383 ratioBkgEff=0.67064 [-1e+30, 3.0252]  in interval = 1
 
NeymanConstruction: Prog: 93/100 total MC = 80 this test stat = 2.16592
 s=111 ratioSigEff=0.976625 ratioBkgEff=0.663286 [-1e+30, 2.93195]  in interval = 1
 
NeymanConstruction: Prog: 94/100 total MC = 80 this test stat = 2.26567
 s=112.2 ratioSigEff=0.975857 ratioBkgEff=0.655962 [-1e+30, 3.15451]  in interval = 1
 
NeymanConstruction: Prog: 95/100 total MC = 80 this test stat = 2.36747
 s=113.4 ratioSigEff=0.975049 ratioBkgEff=0.648489 [-1e+30, 3.05911]  in interval = 1
 
NeymanConstruction: Prog: 96/100 total MC = 80 this test stat = 2.47134
 s=114.6 ratioSigEff=0.97426 ratioBkgEff=0.641206 [-1e+30, 2.96561]  in interval = 1
 
NeymanConstruction: Prog: 97/100 total MC = 80 this test stat = 2.57725
 s=115.8 ratioSigEff=0.973462 ratioBkgEff=0.633952 [-1e+30, 3.5205]  in interval = 1
 
NeymanConstruction: Prog: 98/100 total MC = 720 this test stat = 2.68519
 s=117 ratioSigEff=0.972655 ratioBkgEff=0.626728 [-1e+30, 3.19948]  in interval = 1
 
NeymanConstruction: Prog: 99/100 total MC = 80 this test stat = 2.79514
 s=118.2 ratioSigEff=0.971839 ratioBkgEff=0.619534 [-1e+30, 3.43015]  in interval = 1
 
NeymanConstruction: Prog: 100/100 total MC = 80 this test stat = 2.90706
 s=119.4 ratioSigEff=0.971014 ratioBkgEff=0.61237 [-1e+30, 3.55406]  in interval = 1
 
[#1] INFO:Eval -- 100 points in interval
 
[#1] INFO:Minimization --  Including the following constraint terms in minimization: (sigConstraint,bkgConstraint)
[#1] INFO:Minimization -- The global observables are not defined , normalize constraints with respect to the parameters (b,ratioBkgEff,ratioSigEff,s)
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_modelWithConstraints_exampleData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization --  The following expressions will be evaluated in cache-and-track mode: (countingModel)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:Minimization --  Including the following constraint terms in minimization: (sigConstraint,bkgConstraint)
[#1] INFO:Minimization -- The following global observables have been defined and their values are taken from the model: (gSigEff,gSigBkg)
Metropolis-Hastings progress: ....................................................................................................
[#1] INFO:Eval -- Proposal acceptance rate: 47.705%
[#1] INFO:Eval -- Number of steps in chain: 9541
Real time 0:00:12, CP time 12.420
Profile lower limit on s =  13.949725090292226
Profile upper limit on s =  107.95033326808289
FC lower limit on s =  0.6
FC upper limit on s =  119.39999999999999
MCMC lower limit on s =  18.926872759370006
MCMC upper limit on s =  103.11334757225421
MCMC Actual confidence level:  0.9499523594604082
plotting the chain data - nentries =  9541
plotting the scanned points used in the frequentist construction - npoints =  100

 
import ROOT
 
# --------------------------------------
# An example of setting a limit in a number counting experiment with uncertainty on background and signal
 
# to time the macro
t = ROOT.TStopwatch()
t.Start()
 
# --------------------------------------
# The Model building stage
# --------------------------------------
wspace = ROOT.RooWorkspace()
wspace.factory(
    "Poisson::countingModel(obs[150,0,300], " "sum(s[50,0,120]*ratioSigEff[1.,0,3.],b[100]*ratioBkgEff[1.,0.,3.]))"
)  # counting model
wspace.factory("Gaussian::sigConstraint(gSigEff[1,0,3],ratioSigEff,0.05)")  # 5% signal efficiency uncertainty
wspace.factory("Gaussian::bkgConstraint(gSigBkg[1,0,3],ratioBkgEff,0.2)")  # 10% background efficiency uncertainty
wspace.factory("PROD::modelWithConstraints(countingModel,sigConstraint,bkgConstraint)")  # product of terms
wspace.Print()
 
modelWithConstraints = wspace["modelWithConstraints"]  # get the model
obs = wspace["obs"]  # get the observable
s = wspace["s"]  # get the signal we care about
b = wspace["b"]  # get the background and set it to a constant.  Uncertainty included in ratioBkgEff
b.setConstant()
 
ratioSigEff = wspace["ratioSigEff"]  # get uncertain parameter to constrain
ratioBkgEff = wspace["ratioBkgEff"]  # get uncertain parameter to constrain
constrainedParams = {ratioSigEff, ratioBkgEff}  # need to constrain these in the fit (should change default behavior)
 
gSigEff = wspace["gSigEff"]  # global observables for signal efficiency
gSigBkg = wspace["gSigBkg"]  # global obs for background efficiency
gSigEff.setConstant()
gSigBkg.setConstant()
 
# Create an example dataset with 160 observed events
obs.setVal(160.0)
data = ROOT.RooDataSet("exampleData", "exampleData", {obs})
data.add(obs)
 
# not necessary
modelWithConstraints.fitTo(data, Constrain=constrainedParams, PrintLevel=-1)
 
# Now let's make some confidence intervals for s, our parameter of interest
modelConfig = ROOT.RooStats.ModelConfig(wspace)
modelConfig.SetPdf(modelWithConstraints)
modelConfig.SetParametersOfInterest({s})
modelConfig.SetNuisanceParameters(constrainedParams)
modelConfig.SetObservables(obs)
modelConfig.SetGlobalObservables({gSigEff, gSigBkg})
modelConfig.SetName("ModelConfig")
wspace.Import(modelConfig)
wspace.Import(data)
wspace.SetName("w")
wspace.writeToFile("rs101_ws.root")
 
# First, let's use a Calculator based on the Profile Likelihood Ratio
plc = ROOT.RooStats.ProfileLikelihoodCalculator(data, modelConfig)
plc.SetTestSize(0.05)
lrinterval = plc.GetInterval()
 
# Let's make a plot
dataCanvas = ROOT.TCanvas("dataCanvas")
dataCanvas.Divide(2, 1)
dataCanvas.cd(1)
 
plotInt = ROOT.RooStats.LikelihoodIntervalPlot(lrinterval)
plotInt.SetTitle("Profile Likelihood Ratio and Posterior for S")
plotInt.Draw()
 
# Second, use a Calculator based on the Feldman Cousins technique
fc = ROOT.RooStats.FeldmanCousins(data, modelConfig)
fc.UseAdaptiveSampling(True)
fc.FluctuateNumDataEntries(False)  # number counting analysis: dataset always has 1 entry with N events observed
fc.SetNBins(100)  # number of points to test per parameter
fc.SetTestSize(0.05)
# fc.SaveBeltToFile(True) # optional
fcint = fc.GetInterval()
 
fit = modelWithConstraints.fitTo(data, Save=True, PrintLevel=-1)
 
# Third, use a Calculator based on Markov Chain monte carlo
# Before configuring the calculator, let's make a ProposalFunction
# that will achieve a high acceptance rate
ph = ROOT.RooStats.ProposalHelper()
ph.SetVariables(fit.floatParsFinal())
ph.SetCovMatrix(fit.covarianceMatrix())
ph.SetUpdateProposalParameters(True)
ph.SetCacheSize(100)
pdfProp = ph.GetProposalFunction()
 
mc = ROOT.RooStats.MCMCCalculator(data, modelConfig)
mc.SetNumIters(20000)  # steps to propose in the chain
mc.SetTestSize(0.05)  # 95% CL
mc.SetNumBurnInSteps(40)  # ignore first N steps in chain as "burn in"
mc.SetProposalFunction(pdfProp)
mc.SetLeftSideTailFraction(0.5)  # find a "central" interval
mcInt = mc.GetInterval()
 
# Get Lower and Upper limits from Profile Calculator
print("Profile lower limit on s = ", lrinterval.LowerLimit(s))
print("Profile upper limit on s = ", lrinterval.UpperLimit(s))
 
# Get Lower and Upper limits from FeldmanCousins with profile construction
if fcint:
    fcul = fcint.UpperLimit(s)
    fcll = fcint.LowerLimit(s)
    print("FC lower limit on s = ", fcll)
    print("FC upper limit on s = ", fcul)
    fcllLine = ROOT.TLine(fcll, 0, fcll, 1)
    fculLine = ROOT.TLine(fcul, 0, fcul, 1)
    fcllLine.SetLineColor(ROOT.kRed)
    fculLine.SetLineColor(ROOT.kRed)
    fcllLine.Draw("same")
    fculLine.Draw("same")
    dataCanvas.Update()
 
# Plot MCMC interval and print some statistics
mcPlot = ROOT.RooStats.MCMCIntervalPlot(mcInt)
mcPlot.SetLineColor(ROOT.kMagenta)
mcPlot.SetLineWidth(2)
mcPlot.Draw("same")
 
mcul = mcInt.UpperLimit(s)
mcll = mcInt.LowerLimit(s)
print("MCMC lower limit on s = ", mcll)
print("MCMC upper limit on s = ", mcul)
print("MCMC Actual confidence level: ", mcInt.GetActualConfidenceLevel())
 
# 3-d plot of the parameter points
dataCanvas.cd(2)
 
# also plot the points in the markov chain
chainData = mcInt.GetChainAsDataSet()
 
print("plotting the chain data - nentries = ", chainData.numEntries())
chain = ROOT.RooStats.GetAsTTree("chainTreeData", "chainTreeData", chainData)
chain.SetMarkerStyle(6)
chain.SetMarkerColor(ROOT.kRed)
 
chain.Draw("s:ratioSigEff:ratioBkgEff", "nll_MarkovChain_local_", "box")  # 3-d box proportional to posterior
 
# the points used in the profile construction
parScanData = fc.GetPointsToScan()
print("plotting the scanned points used in the frequentist construction - npoints = ", parScanData.numEntries())
 
gr = ROOT.TGraph2D(parScanData.numEntries())
for ievt in range(parScanData.numEntries()):
    evt = parScanData.get(ievt)
    x = evt.getRealValue("ratioBkgEff")
    y = evt.getRealValue("ratioSigEff")
    z = evt.getRealValue("s")
    gr.SetPoint(ievt, x, y, z)
 
gr.SetMarkerStyle(24)
gr.Draw("P SAME")
 
# print timing info
t.Stop()
t.Print()
 
dataCanvas.SaveAs("rs101_limitexample.png")
 
# TODO: The MCMCCalculator has to be destructed first. Otherwise, we can get
# segmentation faults depending on the destruction order, which is random in
# Python. Probably the issue is that some object has a non-owning pointer to
# another object, which it uses in its destructor. This should be fixed either
# in the design of RooStats in C++, or with phythonizations.
del mc

Date

June 2022

Authors

Artem Busorgin, Kyle Cranmer (C++ version)

Definition in file rs101_limitexample.py.