library: libCore
#include "TMath.h" |
TMath
class description - source file - inheritance tree (.ps)
private:
static Double_t GamCf(Double_t a, Double_t x)
static Double_t GamSer(Double_t a, Double_t x)
public:
TMath()
TMath(const TMath&)
~TMath()
static Short_t Abs(Short_t d)
static Int_t Abs(Int_t d)
static Long_t Abs(Long_t d)
static Long64_t Abs(Long64_t d)
static Float_t Abs(Float_t d)
static Double_t Abs(Double_t d)
static Double_t ACos(Double_t x)
static Double_t ACosH(Double_t)
static Double_t ASin(Double_t x)
static Double_t ASinH(Double_t)
static Double_t ATan(Double_t x)
static Double_t ATan2(Double_t y, Double_t x)
static Double_t ATanH(Double_t)
static Double_t BesselI(Int_t n, Double_t x)
static Double_t BesselI0(Double_t x)
static Double_t BesselI1(Double_t x)
static Double_t BesselJ0(Double_t x)
static Double_t BesselJ1(Double_t x)
static Double_t BesselK(Int_t n, Double_t x)
static Double_t BesselK0(Double_t x)
static Double_t BesselK1(Double_t x)
static Double_t BesselY0(Double_t x)
static Double_t BesselY1(Double_t x)
static Double_t Beta(Double_t p, Double_t q)
static Double_t BetaCf(Double_t x, Double_t a, Double_t b)
static Double_t BetaIncomplete(Double_t x, Double_t a, Double_t b)
static Int_t BinarySearch(Int_t n, const Short_t* array, Short_t value)
static Int_t BinarySearch(Int_t n, const Short_t** array, Short_t value)
static Int_t BinarySearch(Int_t n, const Int_t* array, Int_t value)
static Int_t BinarySearch(Int_t n, const Int_t** array, Int_t value)
static Int_t BinarySearch(Int_t n, const Float_t* array, Float_t value)
static Int_t BinarySearch(Int_t n, const Float_t** array, Float_t value)
static Int_t BinarySearch(Int_t n, const Double_t* array, Double_t value)
static Int_t BinarySearch(Int_t n, const Double_t** array, Double_t value)
static Int_t BinarySearch(Int_t n, const Long_t* array, Long_t value)
static Int_t BinarySearch(Int_t n, const Long_t** array, Long_t value)
static Int_t BinarySearch(Int_t n, const Long64_t* array, Long64_t value)
static Int_t BinarySearch(Int_t n, const Long64_t** array, Long64_t value)
static Double_t Binomial(Int_t n, Int_t k)
static Double_t BinomialI(Double_t p, Int_t n, Int_t k)
static Double_t BreitWigner(Double_t x, Double_t mean = 0, Double_t gamma = 1)
static void BubbleHigh(Int_t Narr, Double_t* arr1, Int_t* arr2)
static void BubbleLow(Int_t Narr, Double_t* arr1, Int_t* arr2)
static Double_t C()
static Double_t Ccgs()
static Double_t Ceil(Double_t x)
static TClass* Class()
static Double_t Cos(Double_t x)
static Double_t CosH(Double_t x)
static Float_t* Cross(Float_t* v1, Float_t* v2, Float_t* out)
static Double_t* Cross(Double_t* v1, Double_t* v2, Double_t* out)
static Double_t CUncertainty()
static Double_t DegToRad()
static Double_t E()
static Double_t Erf(Double_t x)
static Double_t Erfc(Double_t x)
static Double_t ErfcInverse(Double_t x)
static Double_t ErfInverse(Double_t x)
static Bool_t Even(Long_t a)
static Double_t Exp(Double_t x)
static Double_t Factorial(Int_t i)
static Double_t FDist(Double_t F, Double_t N, Double_t M)
static Double_t FDistI(Double_t F, Double_t N, Double_t M)
static Int_t Finite(Double_t x)
static Double_t Floor(Double_t x)
static Double_t Freq(Double_t x)
static Double_t G()
static Double_t Gamma(Double_t z)
static Double_t Gamma(Double_t a, Double_t x)
static Double_t Gaus(Double_t x, Double_t mean = 0, Double_t sigma = 1, Bool_t norm = kFALSE)
static Double_t Gcgs()
static Double_t GeomMean(Int_t n, const Short_t* a)
static Double_t GeomMean(Int_t n, const Int_t* a)
static Double_t GeomMean(Int_t n, const Float_t* a)
static Double_t GeomMean(Int_t n, const Double_t* a)
static Double_t GeomMean(Int_t n, const Long_t* a)
static Double_t GeomMean(Int_t n, const Long64_t* a)
static Double_t GhbarC()
static Double_t GhbarCUncertainty()
static Double_t Gn()
static Double_t GnUncertainty()
static Double_t GUncertainty()
static Double_t H()
static ULong_t Hash(const void* txt, Int_t ntxt)
static ULong_t Hash(const char* str)
static Double_t Hbar()
static Double_t Hbarcgs()
static Double_t HbarUncertainty()
static Double_t HC()
static Double_t HCcgs()
static Double_t Hcgs()
static Double_t HUncertainty()
static Double_t Hypot(Double_t x, Double_t y)
static Long_t Hypot(Long_t x, Long_t y)
static Double_t InvPi()
virtual TClass* IsA() const
static Bool_t IsInside(Double_t xp, Double_t yp, Int_t np, Double_t* x, Double_t* y)
static Bool_t IsInside(Float_t xp, Float_t yp, Int_t np, Float_t* x, Float_t* y)
static Bool_t IsInside(Int_t xp, Int_t yp, Int_t np, Int_t* x, Int_t* y)
static Int_t IsNaN(Double_t x)
static Double_t K()
static Double_t Kcgs()
static Double_t KolmogorovProb(Double_t z)
static Double_t KUncertainty()
static Double_t Landau(Double_t x, Double_t mean = 0, Double_t sigma = 1)
static Double_t Ldexp(Double_t x, Int_t exp)
static Double_t Ln10()
static Double_t LnGamma(Double_t z)
static Int_t LocMax(Int_t n, const Short_t* a)
static Int_t LocMax(Int_t n, const Int_t* a)
static Int_t LocMax(Int_t n, const Float_t* a)
static Int_t LocMax(Int_t n, const Double_t* a)
static Int_t LocMax(Int_t n, const Long_t* a)
static Int_t LocMax(Int_t n, const Long64_t* a)
static Int_t LocMin(Int_t n, const Short_t* a)
static Int_t LocMin(Int_t n, const Int_t* a)
static Int_t LocMin(Int_t n, const Float_t* a)
static Int_t LocMin(Int_t n, const Double_t* a)
static Int_t LocMin(Int_t n, const Long_t* a)
static Int_t LocMin(Int_t n, const Long64_t* a)
static Double_t Log(Double_t x)
static Double_t Log10(Double_t x)
static Double_t Log2(Double_t x)
static Double_t LogE()
static Short_t Max(Short_t a, Short_t b)
static UShort_t Max(UShort_t a, UShort_t b)
static Int_t Max(Int_t a, Int_t b)
static UInt_t Max(UInt_t a, UInt_t b)
static Long_t Max(Long_t a, Long_t b)
static ULong_t Max(ULong_t a, ULong_t b)
static Long64_t Max(Long64_t a, Long64_t b)
static ULong64_t Max(ULong64_t a, ULong64_t b)
static Float_t Max(Float_t a, Float_t b)
static Double_t Max(Double_t a, Double_t b)
static Double_t Mean(Int_t n, const Short_t* a, const Double_t* w = 0)
static Double_t Mean(Int_t n, const Int_t* a, const Double_t* w = 0)
static Double_t Mean(Int_t n, const Float_t* a, const Double_t* w = 0)
static Double_t Mean(Int_t n, const Double_t* a, const Double_t* w = 0)
static Double_t Mean(Int_t n, const Long_t* a, const Double_t* w = 0)
static Double_t Mean(Int_t n, const Long64_t* a, const Double_t* w = 0)
static Short_t Median(Int_t n, const Short_t* a, const Double_t* w = 0, Int_t* work = 0)
static Int_t Median(Int_t n, const Int_t* a, const Double_t* w = 0, Int_t* work = 0)
static Float_t Median(Int_t n, const Float_t* a, const Double_t* w = 0, Int_t* work = 0)
static Double_t Median(Int_t n, const Double_t* a, const Double_t* w = 0, Int_t* work = 0)
static Long_t Median(Int_t n, const Long_t* a, const Double_t* w = 0, Int_t* work = 0)
static Long64_t Median(Int_t n, const Long64_t* a, const Double_t* w = 0, Int_t* work = 0)
static Double_t MedianSorted(Int_t n, Double_t* a)
static Short_t Min(Short_t a, Short_t b)
static UShort_t Min(UShort_t a, UShort_t b)
static Int_t Min(Int_t a, Int_t b)
static UInt_t Min(UInt_t a, UInt_t b)
static Long_t Min(Long_t a, Long_t b)
static ULong_t Min(ULong_t a, ULong_t b)
static Long64_t Min(Long64_t a, Long64_t b)
static ULong64_t Min(ULong64_t a, ULong64_t b)
static Float_t Min(Float_t a, Float_t b)
static Double_t Min(Double_t a, Double_t b)
static Double_t MWair()
static Double_t Na()
static Double_t NaUncertainty()
static Long_t NextPrime(Long_t x)
static Int_t Nint(Float_t x)
static Int_t Nint(Double_t x)
static Float_t* Normal2Plane(Float_t* v1, Float_t* v2, Float_t* v3, Float_t* normal)
static Double_t* Normal2Plane(Double_t* v1, Double_t* v2, Double_t* v3, Double_t* normal)
static Float_t Normalize(Float_t* v)
static Double_t Normalize(Double_t* v)
static Float_t NormCross(Float_t* v1, Float_t* v2, Float_t* out)
static Double_t NormCross(Double_t* v1, Double_t* v2, Double_t* out)
static Bool_t Odd(Long_t a)
TMath& operator=(const TMath&)
static Bool_t Permute(Int_t n, Int_t* a)
static Double_t Pi()
static Double_t PiOver2()
static Double_t PiOver4()
static Double_t Poisson(Double_t x, Double_t par)
static Double_t PoissonI(Double_t x, Double_t par)
static Double_t Power(Double_t x, Double_t y)
static Double_t Prob(Double_t chi2, Int_t ndf)
static Double_t Qe()
static Double_t QeUncertainty()
static Double_t R()
static Double_t RadToDeg()
static Short_t Range(Short_t lb, Short_t ub, Short_t x)
static Int_t Range(Int_t lb, Int_t ub, Int_t x)
static Long_t Range(Long_t lb, Long_t ub, Long_t x)
static ULong_t Range(ULong_t lb, ULong_t ub, ULong_t x)
static Double_t Range(Double_t lb, Double_t ub, Double_t x)
static Double_t Rgair()
static Double_t RMS(Int_t n, const Short_t* a)
static Double_t RMS(Int_t n, const Int_t* a)
static Double_t RMS(Int_t n, const Float_t* a)
static Double_t RMS(Int_t n, const Double_t* a)
static Double_t RMS(Int_t n, const Long_t* a)
static Double_t RMS(Int_t n, const Long64_t* a)
static void RootsCubic(Double_t* coef, Double_t& a, Double_t& b, Double_t& c)
static Double_t RUncertainty()
virtual void ShowMembers(TMemberInspector& insp, char* parent)
static Double_t Sigma()
static Double_t SigmaUncertainty()
static Short_t Sign(Short_t a, Short_t b)
static Int_t Sign(Int_t a, Int_t b)
static Long_t Sign(Long_t a, Long_t b)
static Long64_t Sign(Long64_t a, Long64_t b)
static Float_t Sign(Float_t a, Float_t b)
static Double_t Sign(Double_t a, Double_t b)
static Double_t Sin(Double_t x)
static Double_t SinH(Double_t x)
static void Sort(Int_t n, const Short_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, const Int_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, const Float_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, const Double_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, const Long_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, const Long64_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Long64_t n, const Long64_t* a, Long64_t* index, Bool_t down = kTRUE)
static Double_t Sqrt(Double_t x)
static Long_t Sqrt(Long_t x)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
static Double_t StruveH0(Double_t x)
static Double_t StruveH1(Double_t x)
static Double_t StruveL0(Double_t x)
static Double_t StruveL1(Double_t x)
static Double_t Student(Double_t T, Double_t ndf)
static Double_t StudentI(Double_t T, Double_t ndf)
static Double_t Tan(Double_t x)
static Double_t TanH(Double_t x)
static Double_t TwoPi()
static Double_t Voigt(Double_t x, Double_t sigma, Double_t lg, Int_t R = 4)
TMath
Encapsulate math routines (i.e. provide a kind of namespace).
For the time being avoid templates.
Long_t Sqrt(Long_t x)
Long_t Hypot(Long_t x, Long_t y)
Double_t Hypot(Double_t x, Double_t y)
Double_t ASinH(Double_t x)
Double_t ACosH(Double_t x)
Double_t ATanH(Double_t x)
Double_t Log2(Double_t x)
Long_t NextPrime(Long_t x)
Return next prime number after x, unless x is a prime in which case
x is returned.
Int_t Nint(Float_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Int_t Nint(Double_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Float_t* Cross(Float_t v1[3],Float_t v2[3],Float_t out[3])
Calculate the Cross Product of two vectors:
out = [v1 x v2]
Double_t* Cross(Double_t v1[3],Double_t v2[3],Double_t out[3])
Calculate the Cross Product of two vectors:
out = [v1 x v2]
Double_t Erf(Double_t x)
Computation of the error function erf(x).
Erf(x) = (2/sqrt(pi)) Integral(exp(-t^2))dt between 0 and x
Double_t Erfc(Double_t x)
Compute the complementary error function erfc(x).
Erfc(x) = (2/sqrt(pi)) Integral(exp(-t^2))dt between x and infinity
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t ErfInverse(Double_t x)
returns the inverse error function
x must be <-1<x<1
Double_t Factorial(Int_t n)
Compute factorial(n).
Double_t Freq(Double_t x)
Computation of the normal frequency function freq(x).
Freq(x) = (1/sqrt(2pi)) Integral(exp(-t^2/2))dt between -infinity and x.
Translated from CERNLIB C300 by Rene Brun.
Double_t Gamma(Double_t z)
Computation of gamma(z) for all z>0.
C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Gamma(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t GamCf(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
via its continued fraction representation.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t GamSer(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
via its series representation.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t BreitWigner(Double_t x, Double_t mean, Double_t gamma)
Calculate a Breit Wigner function with mean and gamma.
Double_t Gaus(Double_t x, Double_t mean, Double_t sigma, Bool_t norm)
Calculate a gaussian function with mean and sigma.
If norm=kTRUE (default is kFALSE) the result is divided
by sqrt(2*Pi)*sigma.
Double_t Landau(Double_t x, Double_t mpv, Double_t sigma)
The LANDAU function with mpv(most probable value) and sigma.
This function has been adapted from the CERNLIB routine G110 denlan.
Double_t LnGamma(Double_t z)
Computation of ln[gamma(z)] for all z>0.
C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
The accuracy of the result is better than 2e-10.
--- Nve 14-nov-1998 UU-SAP Utrecht
Float_t Normalize(Float_t v[3])
Normalize a vector v in place.
Returns the norm of the original vector.
Double_t Normalize(Double_t v[3])
Normalize a vector v in place.
Returns the norm of the original vector.
This implementation (thanks Kevin Lynch <krlynch@bu.edu>) is protected
against possible overflows.
Float_t* Normal2Plane(Float_t p1[3],Float_t p2[3],Float_t p3[3], Float_t normal[3])
Calculate a normal vector of a plane.
Input:
Float_t *p1,*p2,*p3 - 3 3D points belonged the plane to define it.
Return:
Pointer to 3D normal vector (normalized)
Double_t* Normal2Plane(Double_t p1[3],Double_t p2[3],Double_t p3[3], Double_t normal[3])
Calculate a normal vector of a plane.
Input:
Float_t *p1,*p2,*p3 - 3 3D points belonged the plane to define it.
Return:
Pointer to 3D normal vector (normalized)
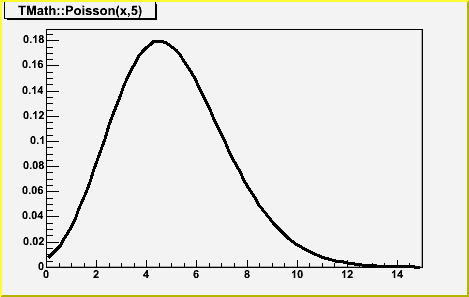
Double_t Poisson(Double_t x, Double_t par)
compute the Poisson distribution function for (x,par)
The Poisson PDF is implemented by means of Euler's Gamma-function
(for the factorial), so for all integer arguments it is correct.
BUT for non-integer values it IS NOT equal to the Poisson distribution.
see TMath::PoissonI to get a non-smooth function.
Note that for large values of par, it is better to call
TMath::Gaus(x,par,sqrt(par),kTRUE)
/*
 */
*/
Double_t PoissonI(Double_t x, Double_t par)
compute the Poisson distribution function for (x,par)
This is a non-smooth function
/*
 */
*/
Double_t Prob(Double_t chi2,Int_t ndf)
Computation of the probability for a certain Chi-squared (chi2)
and number of degrees of freedom (ndf).
Calculations are based on the incomplete gamma function P(a,x),
where a=ndf/2 and x=chi2/2.
P(a,x) represents the probability that the observed Chi-squared
for a correct model should be less than the value chi2.
The returned probability corresponds to 1-P(a,x),
which denotes the probability that an observed Chi-squared exceeds
the value chi2 by chance, even for a correct model.
--- NvE 14-nov-1998 UU-SAP Utrecht
Double_t KolmogorovProb(Double_t z)
Calculates the Kolmogorov distribution function,
/*
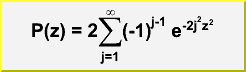 */
*/
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB.
Double_t Voigt(Double_t x, Double_t sigma, Double_t lg, Int_t R)
Computation of Voigt function (normalised).
Voigt is a convolution of
gauss(x) = 1/(sqrt(2*pi)*sigma) * exp(x*x/(2*sigma*sigma)
and
lorentz(x) = (1/pi) * (lg/2) / (x*x + g*g/4)
functions.
The Voigt function is known to be the real part of Faddeeva function also
called complex error function [2].
The algoritm was developed by J. Humlicek [1].
This code is based on fortran code presented by R. J. Wells [2].
Translated and adapted by Miha D. Puc
To calculate the Faddeeva function with relative error less than 10^(-R).
R can be set by the the user subject to the constraints 2 <= R <= 5.
[1] J. Humlicek, JQSRT, 21, 437 (1982).
[2] R.J. Wells "Rapid Approximation to the Voigt/Faddeeva Function and its
Derivatives" JQSRT 62 (1999), pp 29-48.
http://www-atm.physics.ox.ac.uk/user/wells/voigt.html
void RootsCubic(Double_t coef[4],Double_t &a, Double_t &b, Double_t &c)
Computes the roots of a cubic polynomial
coef: Coefficients
a,b,c: references to the roots
Author: Jan Conrad
Int_t LocMin(Int_t n, const Short_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMin(Int_t n, const Int_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMin(Int_t n, const Float_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMin(Int_t n, const Double_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMin(Int_t n, const Long_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMin(Int_t n, const Long64_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Int_t LocMax(Int_t n, const Short_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Int_t LocMax(Int_t n, const Int_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Int_t LocMax(Int_t n, const Float_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Int_t LocMax(Int_t n, const Double_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Int_t LocMax(Int_t n, const Long_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Int_t LocMax(Int_t n, const Long64_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Double_t Mean(Int_t n, const Short_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t Mean(Int_t n, const Int_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t Mean(Int_t n, const Float_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t Mean(Int_t n, const Double_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t Mean(Int_t n, const Long_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t Mean(Int_t n, const Long64_t *a, const Double_t *w)
Return the weighted mean of an array a with length n.
Double_t GeomMean(Int_t n, const Short_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t GeomMean(Int_t n, const Int_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t GeomMean(Int_t n, const Float_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t GeomMean(Int_t n, const Double_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t GeomMean(Int_t n, const Long_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t GeomMean(Int_t n, const Long64_t *a)
Return the geometric mean of an array a with length n.
geometric_mean = (Prod_i=0,n-1 |a[i]|)^1/n
Double_t MedianSorted(Int_t n, Double_t *a)
Return the median of an array a in monotonic order with length n
where median is a number which divides sequence of n numbers
into 2 halves. When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
WARNING; Input array a is modified by this function.
Short_t Median(Int_t n, const Short_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Int_t Median(Int_t n, const Int_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Float_t Median(Int_t n, const Float_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Int_t n, const Double_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Long_t Median(Int_t n, const Long_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Long64_t Median(Int_t n, const Long64_t *a, const Double_t *w, Int_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd, the median is kth element k = (n + 1) / 2.
when n is even the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t RMS(Int_t n, const Short_t *a)
Return the RMS of an array a with length n.
Double_t RMS(Int_t n, const Int_t *a)
Return the RMS of an array a with length n.
Double_t RMS(Int_t n, const Float_t *a)
Return the RMS of an array a with length n.
Double_t RMS(Int_t n, const Double_t *a)
Return the RMS of an array a with length n.
Double_t RMS(Int_t n, const Long_t *a)
Return the RMS of an array a with length n.
Double_t RMS(Int_t n, const Long64_t *a)
Return the RMS of an array a with length n.
Int_t BinarySearch(Int_t n, const Short_t *array, Short_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Short_t **array, Short_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Int_t *array, Int_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Int_t **array, Int_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Float_t *array, Float_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Float_t **array, Float_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Double_t *array, Double_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Double_t **array, Double_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Long_t *array, Long_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Long_t **array, Long_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Long64_t *array, Long64_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, const Long64_t **array, Long64_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Bool_t IsInside(Double_t xp, Double_t yp, Int_t np, Double_t *x, Double_t *y)
Function which returns kTRUE if point xp,yp lies inside the
polygon defined by the np points in arrays x and y, kFALSE otherwise
NOTE that the polygon must be a closed polygon (1st and last point
must be identical)
Bool_t IsInside(Float_t xp, Float_t yp, Int_t np, Float_t *x, Float_t *y)
Function which returns kTRUE if point xp,yp lies inside the
polygon defined by the np points in arrays x and y, kFALSE otherwise
NOTE that the polygon must be a closed polygon (1st and last point
must be identical)
Bool_t IsInside(Int_t xp, Int_t yp, Int_t np, Int_t *x, Int_t *y)
Function which returns kTRUE if point xp,yp lies inside the
polygon defined by the np points in arrays x and y, kFALSE otherwise
NOTE that the polygon must be a closed polygon (1st and last point
must be identical)
void Sort(Int_t n1, const Short_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Short_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Int_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Int_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Float_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Float_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Double_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Double_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Long_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Long_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Long64_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Long64_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void BubbleHigh(Int_t Narr, Double_t *arr1, Int_t *arr2)
Bubble sort variant to obtain the order of an array's elements into
an index in order to do more useful things than the standard built
in functions.
*arr1 is unchanged;
*arr2 is the array of indicies corresponding to the decending value
of arr1 with arr2[0] corresponding to the largest arr1 value and
arr2[Narr] the smallest.
Author: Adrian Bevan (bevan@slac.stanford.edu)
Copyright: Liverpool University, July 2001
void BubbleLow(Int_t Narr, Double_t *arr1, Int_t *arr2)
Opposite ordering of the array arr2[] to that of BubbleHigh.
Author: Adrian Bevan (bevan@slac.stanford.edu)
Copyright: Liverpool University, July 2001
ULong_t Hash(const void *txt, Int_t ntxt)
Calculates hash index from any char string.
Based on precalculated table of 256 specially selected random numbers.
For string: i = TMath::Hash(string,nstring);
For int: i = TMath::Hash(&intword,sizeof(int));
For pointer: i = TMath::Hash(&pointer,sizeof(void*));
Limitation: for ntxt>256 calculates hash only from first 256 bytes
V.Perev
ULong_t Hash(const void *txt, Int_t ntxt)
Calculates hash index from any char string.
Based on precalculated table of 256 specially selected numbers.
These numbers are selected in such a way, that for string
length == 4 (integer number) the hash is unambigous, i.e.
from hash value we can recalculate input (no degeneration).
The quality of hash method is good enough, that
"random" numbers made as R = Hash(1), Hash(2), ...Hash(N)
tested by <R>, <R*R>, <Ri*Ri+1> gives the same result
as for libc rand().
For string: i = TMath::Hash(string,nstring);
For int: i = TMath::Hash(&intword,sizeof(int));
For pointer: i = TMath::Hash(&pointer,sizeof(void*));
V.Perev
ULong_t Hash(const char *txt)
Double_t BesselI0(Double_t x)
Compute the modified Bessel function I_0(x) for any real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK0(Double_t x)
Compute the modified Bessel function K_0(x) for positive real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI1(Double_t x)
Compute the modified Bessel function I_1(x) for any real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK1(Double_t x)
Compute the modified Bessel function K_1(x) for positive real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK(Int_t n,Double_t x)
Compute the Integer Order Modified Bessel function K_n(x)
for n=0,1,2,... and positive real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI(Int_t n,Double_t x)
Compute the Integer Order Modified Bessel function I_n(x)
for n=0,1,2,... and any real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselJ0(Double_t x)
Returns the Bessel function J0(x) for any real x.
Double_t BesselJ1(Double_t x)
Returns the Bessel function J1(x) for any real x.
Double_t BesselY0(Double_t x)
Returns the Bessel function Y0(x) for positive x.
Double_t BesselY1(Double_t x)
Returns the Bessel function Y1(x) for positive x.
Double_t StruveH0(Double_t x)
Struve Functions of Order 0
Converted from CERNLIB M342 by Rene Brun.
Double_t StruveH1(Double_t x)
Struve Functions of Order 1
Converted from CERNLIB M342 by Rene Brun.
Double_t StruveL0(Double_t x)
Modified Struve Function of Order 0.
By Kirill Filimonov.
Double_t StruveL1(Double_t x)
Modified Struve Function of Order 1.
By Kirill Filimonov.
Double_t Beta(Double_t p, Double_t q)
Calculates Beta-function Gamma(p)*Gamma(q)/Gamma(p+q) .
Double_t BetaCf(Double_t x, Double_t a, Double_t b)
Continued fraction evaluation by modified Lentz's method
used in calculation of incomplete Beta function.
Double_t BetaIncomplete(Double_t x, Double_t a, Double_t b)
Calculates the incomplete Beta-function.
--implementation by Anna Kreshuk
Double_t Binomial(Int_t n,Int_t k)
Calculate the binomial coefficient n over k.
Double_t BinomialI(Double_t p, Int_t n, Int_t k)
Suppose an event occurs with probability _p_ per trial
Then the probability P of its occuring _k_ or more times
in _n_ trials is termed a cumulative binomial probability
the formula is P = sum_from_j=k_to_n(TMath::Binomial(n, j)*
*TMath::Power(p, j)*TMath::Power(1-p, n-j)
For _n_ larger than 12 BetaIncomplete is a much better way
to evaluate the sum than would be the straightforward sum calculation
for _n_ smaller than 12 either method is acceptable
("Numerical Recipes")
--implementation by Anna Kreshuk
Double_t FDist(Double_t F, Double_t N, Double_t M)
Computes the density function of F-distribution
(probability function, integral of density, is computed in FDistI)
parameters N and M stand for degrees of freedom of chi-squares
mentioned above
parameter F is the actual variable x of the density function p(x)
and the point at which the density function is calculated.
about F distribution:
F-distribution arises in testing whether two random samples
have the same variance. It is the ratio of two chi-square
distributions, with N and M degrees of freedom respectively,
where each chi-square is first divided by it's number of degrees
of freedom.
--implementation by Anna Kreshuk
Double_t FDistI(Double_t F, Double_t N, Double_t M)
Calculates the cumulative distribution function of F-distribution
this function occurs in the statistical test of whether two observed
samples have the same variance. For this test a certain statistic F, the ratio of
observed dispersion fo the first sample to that of the second sample,
is calculated. N and M stand for numbers of degrees of freedom in the samples
1-FDistI() is the significance level at which the hypothesis "1 has smaller
variance than 2" can be rejected. A small numerical value of 1 - FDistI() implies
a very significant rejection, in turn implying high confidence in the hypothesis
"1 has variance greater than 2".
--implementation by Anna Kreshuk
Bool_t Permute(Int_t n, Int_t *a)
Simple recursive algorithm to find the permutations of
n natural numbers, not necessarily all distinct
adapted from CERNLIB routine PERMU
The input array has to be initialised with a non descending
sequence. The method returns kFALSE when
all combinations are exhausted
Double_t Student(Double_t T, Double_t ndf)
Computes density function for Student's t- distribution
(the probability function (integral of density) is computed in StudentI)
First parameter stands for x - the actual variable of the
density function p(x) and the point at which the density is calculated.
Second parameter stands for number of degrees of freedom
About Student distribution:
Student's t-distribution is used for many significance tests, for example,
for the Student's t-tests for the statistical significance of difference
between two sample means and for confidence intervals for the difference
between two population means.
Example: suppose we have a random sample of size n drawn from normal
distribution with mean Mu and st.deviation Sigma. Then the variable
t = (sample_mean - Mu)/(sample_deviation / sqrt(n))
has Student's t-distribution with n-1 degrees of freedom
NOTE that this function's second argument is number of degrees of freedom,
not the sample size.
As the number of degrees of freedom grows, t-distribution approaches
Normal(0,1) distribution.
--implementation by Anna Kreshuk
Double_t StudentI(Double_t T, Double_t ndf)
Calculates the cumulative distribution function of Student's t-distribution
second parameter stands for number of degrees of freedom, not for the number
of samples
if x has Student's t-distribution, the function returns the probability of
x being less than T
--implementation by Anna Kreshuk
Inline Functions
void ~TMath()
Double_t Pi()
Double_t TwoPi()
Double_t PiOver2()
Double_t PiOver4()
Double_t InvPi()
Double_t RadToDeg()
Double_t DegToRad()
Double_t E()
Double_t Ln10()
Double_t LogE()
Double_t C()
Double_t Ccgs()
Double_t CUncertainty()
Double_t G()
Double_t Gcgs()
Double_t GUncertainty()
Double_t GhbarC()
Double_t GhbarCUncertainty()
Double_t Gn()
Double_t GnUncertainty()
Double_t H()
Double_t Hcgs()
Double_t HUncertainty()
Double_t Hbar()
Double_t Hbarcgs()
Double_t HbarUncertainty()
Double_t HC()
Double_t HCcgs()
Double_t K()
Double_t Kcgs()
Double_t KUncertainty()
Double_t Sigma()
Double_t SigmaUncertainty()
Double_t Na()
Double_t NaUncertainty()
Double_t R()
Double_t RUncertainty()
Double_t MWair()
Double_t Rgair()
Double_t Qe()
Double_t QeUncertainty()
Double_t Sin(Double_t x)
Double_t Cos(Double_t x)
Double_t Tan(Double_t x)
Double_t SinH(Double_t x)
Double_t CosH(Double_t x)
Double_t TanH(Double_t x)
Double_t ASin(Double_t x)
Double_t ACos(Double_t x)
Double_t ATan(Double_t x)
Double_t ATan2(Double_t y, Double_t x)
Double_t Ceil(Double_t x)
Double_t Floor(Double_t x)
Double_t Exp(Double_t x)
Double_t Ldexp(Double_t x, Int_t exp)
Double_t Power(Double_t x, Double_t y)
Double_t Log(Double_t x)
Double_t Log10(Double_t x)
Int_t Finite(Double_t x)
Int_t IsNaN(Double_t x)
Long_t Sqrt(Long_t x)
Short_t Abs(Short_t d)
Int_t Abs(Int_t d)
Long_t Abs(Long_t d)
Long64_t Abs(Long64_t d)
Float_t Abs(Float_t d)
Double_t Abs(Double_t d)
Bool_t Even(Long_t a)
Bool_t Odd(Long_t a)
Short_t Sign(Short_t a, Short_t b)
Int_t Sign(Int_t a, Int_t b)
Long_t Sign(Long_t a, Long_t b)
Long64_t Sign(Long64_t a, Long64_t b)
Float_t Sign(Float_t a, Float_t b)
Double_t Sign(Double_t a, Double_t b)
Short_t Min(Short_t a, Short_t b)
UShort_t Min(UShort_t a, UShort_t b)
Int_t Min(Int_t a, Int_t b)
UInt_t Min(UInt_t a, UInt_t b)
Long_t Min(Long_t a, Long_t b)
ULong_t Min(ULong_t a, ULong_t b)
Long64_t Min(Long64_t a, Long64_t b)
ULong64_t Min(ULong64_t a, ULong64_t b)
Float_t Min(Float_t a, Float_t b)
Double_t Min(Double_t a, Double_t b)
Short_t Max(Short_t a, Short_t b)
UShort_t Max(UShort_t a, UShort_t b)
Int_t Max(Int_t a, Int_t b)
UInt_t Max(UInt_t a, UInt_t b)
Long_t Max(Long_t a, Long_t b)
ULong_t Max(ULong_t a, ULong_t b)
Long64_t Max(Long64_t a, Long64_t b)
ULong64_t Max(ULong64_t a, ULong64_t b)
Float_t Max(Float_t a, Float_t b)
Double_t Max(Double_t a, Double_t b)
Short_t Range(Short_t lb, Short_t ub, Short_t x)
Int_t Range(Int_t lb, Int_t ub, Int_t x)
Long_t Range(Long_t lb, Long_t ub, Long_t x)
ULong_t Range(ULong_t lb, ULong_t ub, ULong_t x)
Double_t Range(Double_t lb, Double_t ub, Double_t x)
Float_t NormCross(Float_t* v1, Float_t* v2, Float_t* out)
Double_t NormCross(Double_t* v1, Double_t* v2, Double_t* out)
Double_t ErfcInverse(Double_t x)
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
TMath TMath()
TMath TMath(const TMath&)
TMath& operator=(const TMath&)
Author: Fons Rademakers 29/07/95
Last update: root/base:$Name: $:$Id: TMath.cxx,v 1.72 2004/07/09 17:40:32 brun Exp $
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
*/
 */
*/
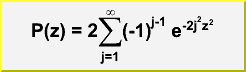 */
*/