// @(#)root/geom:$Name: $:$Id: TGeoMatrix.cxx,v 1.20 2004/02/10 08:56:20 brun Exp $
// Author: Andrei Gheata 25/10/01
/*************************************************************************
* Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
* All rights reserved. *
* *
* For the licensing terms see $ROOTSYS/LICENSE. *
* For the list of contributors see $ROOTSYS/README/CREDITS. *
*************************************************************************/
// Author : Andrei Gheata - Wed 24 Oct 2001 09:46:13 AM CEST
////////////////////////////////////////////////////////////////////////////////
// Geometrical transformation package.
//
// All geometrical transformations handled by the modeller are provided as a
// built-in package. This was designed to minimize memory requirements and
// optimize performance of point/vector master-to-local and local-to-master
// computation. We need to have in mind that a transformation in TGeo has 2
// major use-cases. The first one is for defining the placement of a volume
// with respect to its container reference frame. This frame will be called
// 'master' and the frame of the positioned volume - 'local'. If T is a
// transformation used for positioning volume daughters, then:
//
// MASTER = T * LOCAL
//
// Therefore a local-to-master conversion will be performed by using T, while
// a master-to-local by using its inverse. The second use case is the computation
// of the global transformation of a given object in the geometry. Since the
// geometry is built as 'volumes-inside-volumes', this global transformation
// represent the pile-up of all local transformations in the corresponding
// branch. The conversion from the global reference frame and the given object
// is also called master-to-local, but it is handled by the manager class.
// A general homogenous transformation is defined as a 4x4 matrix embeeding
// a rotation, a translation and a scale. The advantage of this description
// is that each basic transformation can be represented as a homogenous matrix,
// composition being performed as simple matrix multiplication.
// Rotation: Inverse rotation:
// r11 r12 r13 0 r11 r21 r31 0
// r21 r22 r23 0 r12 r22 r32 0
// r31 r32 r33 0 r13 r23 r33 0
// 0 0 0 1 0 0 0 1
//
// Translation: Inverse translation:
// 1 0 0 0 1 0 0 0
// 0 1 0 0 0 1 0 0
// 0 0 1 0 0 0 1 0
// tx ty tz 1 -tx -ty -tz 1
//
// Scale: Inverse scale:
// sx 0 0 0 1/sx 0 0 0
// 0 sy 0 0 0 1/sy 0 0
// 0 0 sz 0 0 0 1/sz 0
// 0 0 0 1 0 0 0 1
//
// where: rij are the 3x3 rotation matrix components,
// tx, ty, tz are the translation components
// sx, sy, sz are arbitrary scale constants on the eacks axis,
//
// The disadvantage in using this approach is that computation for 4x4 matrices
// is expensive. Even combining two translation would become a multiplication
// of their corresponding matrices, which is quite an undesired effect. On the
// other hand, it is not a good idea to store a translation as a block of 16
// numbers. We have therefore chosen to implement each basic transformation type
// as a class deriving from the same basic abstract class and handling its specific
// data and point/vector transformation algorithms.
//
//
/*
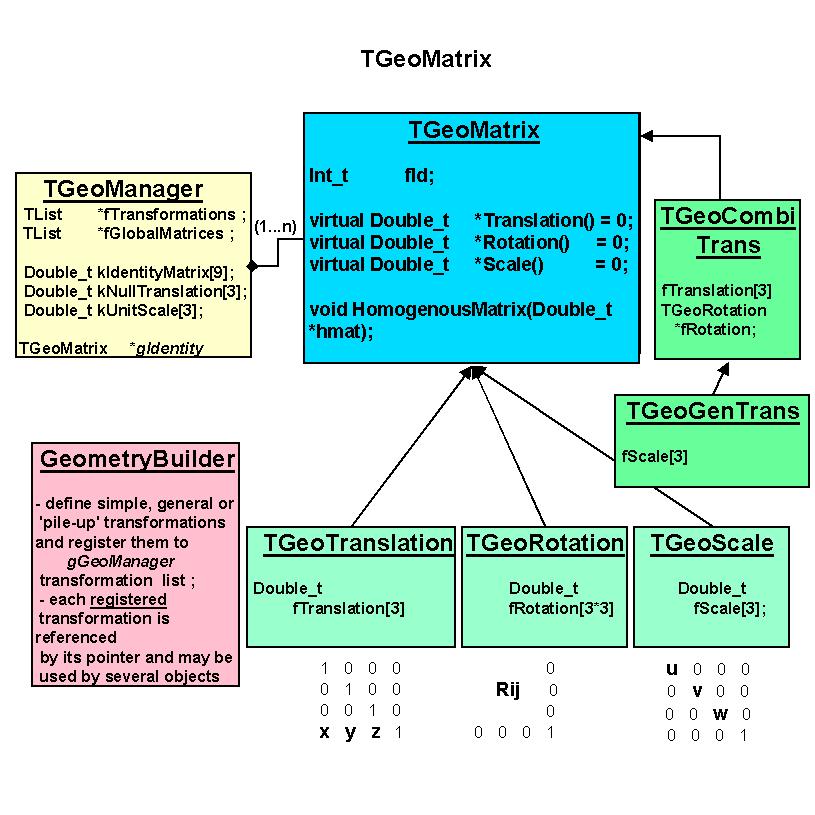 */
//
//
// The base class TGeoMatrix defines abstract metods for:
//
// - translation, rotation and scale getters. Every derived class stores only
// its specific data, e.g. a translation stores an array of 3 doubles and a
// rotation an array of 9. However, asking which is the rotation array of a
// TGeoTranslation through the base TGeoMatrix interface is a legal operation.
// The answer in this case is a pointer to a global constant array representing
// an identity rotation.
// Double_t *TGeoMatrix::GetTranslation()
// Double_t *TGeoMatrix::GetRotation()
// Double_t *TGeoMatrix::GetScale()
//
// - MasterToLocal() and LocalToMaster() point and vector transformations :
// void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master)
// void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master)
// These allow correct conversion also for reflections.
// - Transformation type getters :
// Bool_t TGeoMatrix::IsIdentity()
// Bool_t TGeoMatrix::IsTranslation()
// Bool_t TGeoMatrix::IsRotation()
// Bool_t TGeoMatrix::IsScale()
// Bool_t TGeoMatrix::IsCombi() (translation + rotation)
// Bool_t TGeoMatrix::IsGeneral() (translation + rotation + scale)
//
// Combinations of basic transformations are represented by specific classes
// deriving from TGeoMatrix. In order to define a matrix as a combination of several
// others, a special class TGeoHMatrix is provided. Here is an example of matrix
// creation :
//
// Matrix creation example:
//
// root[0] TGeoRotation r1,r2;
// r1.SetAngles(90,0,30); // rotation defined by Euler angles
// r2.SetAngles(90,90,90,180,0,0); // rotation defined by GEANT3 angles
// TGeoTranslation t1(-10,10,0);
// TGeoTranslation t2(10,-10,5);
// TGeoCombiTrans c1(t1,r1);
// TGeoCombiTrans c2(t2,r2);
// TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix class
// root[7] TGeoHMatrix *ph = new TGeoHMatrix(hm); // this is the one we want to
// // use for positioning a volume
// root[8] ph->Print();
// ...
// pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by the manager
//
// Rule for matrix creation:
// - unless explicitly used for positioning nodes (TGeoVolume::AddNode()) all
// matrices deletion have to be managed by users. Matrices passed to geometry
// have to be created by using new() operator and their deletion is done by
// TGeoManager class.
//
// Available geometrical transformations
//
// 1. TGeoTranslation - represent a (dx,dy,dz) translation. Data members:
// Double_t fTranslation[3]. Translations can be added/subtracted.
// TGeoTranslation t1;
// t1->SetTranslation(-5,10,4);
// TGeoTranslation *t2 = new TGeoTranslation(4,3,10);
// t2->Subtract(&t1);
//
// 2. Rotations - represent a pure rotation. Data members: Double_t fRotationMatrix[3*3].
// Rotations can be defined either by Euler angles, either, by GEANT3 angles :
// TGeoRotation *r1 = new TGeoRotation();
// r1->SetAngles(phi, theta, psi); // all angles in degrees
// This represent the composition of : first a rotation about Z axis with
// angle phi, then a rotation with theta about the rotated X axis, and
// finally a rotation with psi about the new Z axis.
//
// r1->SetAngles(th1,phi1, th2,phi2, th3,phi3)
// This is a rotation defined in GEANT3 style. Theta and phi are the spherical
// angles of each axis of the rotated coordinate system with respect to the
// initial one. This construction allows definition of malformed rotations,
// e.g. not orthogonal. A check is performed and an error message is issued
// in this case.
//
// Specific utilities : determinant, inverse.
//
// 3. Scale transformations - represent a scale shrinking/enlargement. Data
// members :Double_t fScale[3]. Not fully implemented yet.
//
// 4. Combined transformations - represent a rotation folowed by a translation.
// Data members: Double_t fTranslation[3], TGeoRotation *fRotation.
// TGeoRotation *rot = new TGeoRotation("rot",10,20,30);
// TGeoTranslation trans;
// ...
// TGeoCombiTrans *c1 = new TGeoCombiTrans(trans, rot);
// TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot)
//
// 5. TGeoGenTrans - combined transformations including a scale. Not implemented.
// 6. TGeoIdentity - a generic singleton matrix representing a identity transformation
// NOTE: identified by the global variable gGeoIdentity.
//
//
#include "TObjArray.h"
#include "TGeoManager.h"
#include "TGeoMatrix.h"
TGeoIdentity *gGeoIdentity = 0;
const Int_t kN3 = 3*sizeof(Double_t);
const Int_t kN9 = 9*sizeof(Double_t);
// statics and globals
ClassImp(TGeoMatrix)
ClassImp(TGeoTranslation)
ClassImp(TGeoRotation)
ClassImp(TGeoScale)
ClassImp(TGeoCombiTrans)
ClassImp(TGeoGenTrans)
ClassImp(TGeoIdentity)
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix()
{
// dummy constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix(const char *name)
:TNamed(name, "")
{
// Constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::~TGeoMatrix()
{
// Destructor
if (IsRegistered() && gGeoManager) {
if (gGeoManager->GetListOfVolumes()) {
gGeoManager->GetListOfMatrices()->Remove(this);
Error("dtor", "a registered matrix was removed !!!");
}
}
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoMatrix::operator*(const TGeoMatrix &right) const
{
// Multiplication
static TGeoHMatrix h;
h = *this;
h.Multiply(&right);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoMatrix::IsRotAboutZ() const
{
// Returns true if no rotation or the rotation is about Z axis
if (IsIdentity()) return kTRUE;
const Double_t *rot = GetRotationMatrix();
if (TMath::Abs(rot[6])>1E-9) return kFALSE;
if (TMath::Abs(rot[7])>1E-9) return kFALSE;
if ((1.-TMath::Abs(rot[8]))>1E-9) return kFALSE;
return kTRUE;
}
//-----------------------------------------------------------------------------
Int_t TGeoMatrix::GetByteCount() const
{
// Get total size in bytes of this
Int_t count = 4+28+strlen(GetName())+strlen(GetTitle()); // fId + TNamed
if (IsTranslation()) count += 12;
if (IsScale()) count += 12;
if (IsCombi() || IsGeneral()) count += 4 + 36;
return count;
}
//-----------------------------------------------------------------------------
void TGeoMatrix::GetHomogenousMatrix(Double_t *hmat) const
{
// The homogenous matrix associated with the transformation is used for
// piling up's and visualization. A homogenous matrix is a 4*4 array
// containing the translation, the rotation and the scale components
//
// | R00*sx R01 R02 dx |
// | R10 R11*sy R12 dy |
// | R20 R21 R22*sz dz |
// | 0 0 0 1 |
//
// where Rij is the rotation matrix, (sx, sy, sz) is the scale
// transformation and (dx, dy, dz) is the translation.
Double_t *hmatrix = hmat;
const Double_t *mat = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
memcpy(hmatrix, mat, kN3);
mat += 3;
hmatrix += 3;
*hmatrix = 0.0;
hmatrix++;
}
memcpy(hmatrix, GetTranslation(), kN3);
hmatrix = hmat;
if (IsScale()) {
for (Int_t i=0; i<3; i++) {
*hmatrix *= GetScale()[i];
hmatrix += 5;
}
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = tr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = bombtr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
Double_t mt0 = master[0]-tr[0];
Double_t mt1 = master[1]-tr[1];
Double_t mt2 = master[2]-tr[2];
local[0] = mt0*rot[0] + mt1*rot[3] + mt2*rot[6];
local[1] = mt0*rot[1] + mt1*rot[4] + mt2*rot[7];
local[2] = mt0*rot[2] + mt1*rot[5] + mt2*rot[8];
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = (master[0]-bombtr[0])*rot[i]
+ (master[1]-bombtr[1])*rot[i+3]
+ (master[2]-bombtr[2])*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::Print(Option_t *) const
{
// print the matrix in 4x4 format
const Double_t *rot = GetRotationMatrix();
const Double_t *tr = GetTranslation();
const Double_t *sc = GetScale();
printf("matrix %s - translation : %i rotation : %i scale : %in", GetName(),(Int_t)IsTranslation(),
(Int_t)IsRotation(), (Int_t)IsScale());
printf(" %g %g %g %gn", rot[0], rot[1], rot[2], (Double_t)0);
printf(" %g %g %g %gn", rot[3], rot[4], rot[5], (Double_t)0);
printf(" %g %g %g %gn", rot[6], rot[7], rot[8], (Double_t)0);
printf(" %g %g %g %gn", tr[0], tr[1], tr[2], (Double_t)1);
if (IsScale()) printf("Scale : %g %g %gn", sc[0], sc[1], sc[2]);
}
//-----------------------------------------------------------------------------
void TGeoMatrix::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::SetDefaultName()
{
// If no name was supplied in the ctor, the type of transformation is checked.
// A letter will be prepended to the name :
// t - translation
// r - rotation
// s - scale
// c - combi (translation + rotation)
// g - general (tr+rot+scale)
// The index of the transformation in gGeoManager list of transformations will
// be appended.
if (!gGeoManager) return;
if (strlen(GetName())) return;
char type = 'n';
if (IsTranslation()) type = 't';
if (IsRotation()) type = 'r';
if (IsScale()) type = 's';
if (IsCombi()) type = 'c';
if (IsGeneral()) type = 'g';
TObjArray *matrices = gGeoManager->GetListOfMatrices();
Int_t index = 0;
if (matrices) index =matrices->GetEntriesFast() - 1;
Int_t digits = 1;
Int_t num = 10;
while ((Int_t)(index/num)) {
digits++;
num *= 10;
}
char *name = new char[digits+2];
sprintf(name, "%c%i", type, index);
SetName(name);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation()
{
// Default constructor
SetBit(kGeoTranslation);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const TGeoTranslation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoTranslation);
const Double_t *transl = other.GetTranslation();
memcpy(fTranslation, transl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix("")
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetDefaultName();
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const char *name, Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix(name)
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoTranslation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
return h;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Add(const TGeoTranslation *other)
{
// Adding a translation to this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] += trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Subtract(const TGeoTranslation *other)
{
// Subtracting a translation from this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] -= trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// Set translation components
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
master[i] = tr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector to MARS
memcpy(master, local, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
master[i] = bombtr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
local[i] = master[i]-tr[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a vector from MARS to local
memcpy(local, master, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
local[i] = master[i]-bombtr[i];
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation()
{
// Default constructor.
SetBit(kGeoRotation);
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const TGeoRotation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoRotation);
SetRotation(other);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name)
:TGeoMatrix(name)
{
// Named rotation constructor
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
SetBit(kGeoRotation);
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t phi, Double_t theta, Double_t psi)
:TGeoMatrix(name)
{
// Default rotation constructor with Euler angles. Phi is the rotation angle about
// Z axis and is done first, theta is the rotation about new Y and is done
// second, psi is the rotation angle about new Z and is done third. All angles are in
// degrees.
SetBit(kGeoRotation);
SetAngles(phi, theta, psi);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
:TGeoMatrix(name)
{
// Rotation constructor a la GEANT3. Angles theta(i), phi(i) are the polar and azimuthal
// angles of the (i) axis of the rotated system with respect to the initial non-rotated
// system.
// Example : the identity matrix (no rotation) is composed by
// theta1=90, phi1=0, theta2=90, phi2=90, theta3=0, phi3=0
SetBit(kGeoRotation);
SetAngles(theta1, phi1, theta2, phi2, theta3, phi3);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoRotation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoRotation::IsValid() const
{
// Perform orthogonality test for rotation.
const Double_t *r = fRotationMatrix;
Double_t cij;
for (Int_t i=0; i<2; i++) {
for (Int_t j=i+1; j<3; j++) {
// check columns
cij = TMath::Abs(r[i]*r[j]+r[i+3]*r[j+3]+r[i+6]*r[j+6]);
if (cij>1E-4) return kFALSE;
// check rows
cij = TMath::Abs(r[3*i]*r[3*j]+r[3*i+1]*r[3*j+1]+r[3*i+2]*r[3*j+2]);
if (cij>1E-4) return kFALSE;
}
}
return kTRUE;
}
//-----------------------------------------------------------------------------
void TGeoRotation::Clear(Option_t *)
{
// reset data members to 0
memset(&fRotationMatrix[0], 0, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::FastRotZ(Double_t *sincos)
{
fRotationMatrix[0] = sincos[1];
fRotationMatrix[1] = -sincos[0];
fRotationMatrix[3] = sincos[0];
fRotationMatrix[4] = sincos[1];
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::GetPhiRotation() const
{
//--- Returns rotation angle about Z axis in degrees.
Double_t phi = 180.*TMath::ATan2(fRotationMatrix[1], fRotationMatrix[0])/TMath::Pi();
return phi;
}
//-----------------------------------------------------------------------------
void TGeoRotation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetRotation(const TGeoRotation &other)
{
// Copy rotation elements from other rotation matrix.
const Double_t *rot = other.GetRotationMatrix();
memcpy(fRotationMatrix, rot, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t phi, Double_t theta, Double_t psi)
{
// Set matrix elements according to Euler angles
Double_t degrad = TMath::Pi()/180.;
Double_t sinphi = TMath::Sin(degrad*phi);
Double_t cosphi = TMath::Cos(degrad*phi);
Double_t sinthe = TMath::Sin(degrad*theta);
Double_t costhe = TMath::Cos(degrad*theta);
Double_t sinpsi = TMath::Sin(degrad*psi);
Double_t cospsi = TMath::Cos(degrad*psi);
fRotationMatrix[0] = cospsi*cosphi - costhe*sinphi*sinpsi;
fRotationMatrix[1] = -sinpsi*cosphi - costhe*sinphi*cospsi;
fRotationMatrix[2] = sinthe*sinphi;
fRotationMatrix[3] = cospsi*sinphi + costhe*cosphi*sinpsi;
fRotationMatrix[4] = -sinpsi*sinphi + costhe*cosphi*cospsi;
fRotationMatrix[5] = -sinthe*cosphi;
fRotationMatrix[6] = sinpsi*sinthe;
fRotationMatrix[7] = cospsi*sinthe;
fRotationMatrix[8] = costhe;
if (!IsValid()) Error("SetAngles", "invalid rotation (Euler angles : phi=%f theta=%f psi=%f)",phi,theta,psi);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
{
// Set matrix elements in the GEANT3 way
Double_t degrad = TMath::Pi()/180.;
fRotationMatrix[0] = TMath::Cos(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[3] = TMath::Sin(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[6] = TMath::Cos(degrad*theta1);
fRotationMatrix[1] = TMath::Cos(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[4] = TMath::Sin(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[7] = TMath::Cos(degrad*theta2);
fRotationMatrix[2] = TMath::Cos(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[5] = TMath::Sin(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[8] = TMath::Cos(degrad*theta3);
// do the trick to eliminate most of the floating point errors
for (Int_t i=0; i<9; i++) {
if (TMath::Abs(fRotationMatrix[i])<1E-15) fRotationMatrix[i] = 0;
if (TMath::Abs(fRotationMatrix[i]-1)<1E-15) fRotationMatrix[i] = 1;
if (TMath::Abs(fRotationMatrix[i]+1)<1E-15) fRotationMatrix[i] = -1;
}
if (!IsValid()) Error("SetAngles", "invalid rotation (G3 angles, th1=%f phi1=%f, th2=%f ph2=%f, th3=%f phi3=%f)",
theta1,phi1,theta2,phi2,theta3,phi3);
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetAngles(Double_t &theta1, Double_t &phi1, Double_t &theta2, Double_t &phi2,
Double_t &theta3, Double_t &phi3) const
{
// Retreive rotation angles
Double_t raddeg = 180./TMath::Pi();
theta1 = raddeg*TMath::ACos(fRotationMatrix[6]);
theta2 = raddeg*TMath::ACos(fRotationMatrix[7]);
theta3 = raddeg*TMath::ACos(fRotationMatrix[8]);
if (TMath::Abs(fRotationMatrix[0])<1E-6 && TMath::Abs(fRotationMatrix[3])<1E-6) phi1=0.;
else phi1 = raddeg*TMath::ATan2(fRotationMatrix[3],fRotationMatrix[0]);
if (phi1<0) phi1+=360.;
if (TMath::Abs(fRotationMatrix[1])<1E-6 && TMath::Abs(fRotationMatrix[4])<1E-6) phi2=0.;
else phi2 = raddeg*TMath::ATan2(fRotationMatrix[4],fRotationMatrix[1]);
if (phi2<0) phi2+=360.;
if (TMath::Abs(fRotationMatrix[2])<1E-6 && TMath::Abs(fRotationMatrix[5])<1E-6) phi3=0.;
else phi3 = raddeg*TMath::ATan2(fRotationMatrix[5],fRotationMatrix[2]);
if (phi3<0) phi3+=360.;
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::Determinant() const
{
// computes determinant of the rotation matrix
Double_t
det = fRotationMatrix[0]*fRotationMatrix[4]*fRotationMatrix[8] +
fRotationMatrix[3]*fRotationMatrix[7]*fRotationMatrix[1] +
fRotationMatrix[6]*fRotationMatrix[1]*fRotationMatrix[5] -
fRotationMatrix[2]*fRotationMatrix[4]*fRotationMatrix[6] -
fRotationMatrix[5]*fRotationMatrix[7]*fRotationMatrix[0] -
fRotationMatrix[7]*fRotationMatrix[1]*fRotationMatrix[3];
return det;
}
//-----------------------------------------------------------------------------
void TGeoRotation::CheckMatrix()
{
// performes an orthogonality check and finds if the matrix is a reflection
// Warning("CheckMatrix", "orthogonality check not performed yet");
if (Determinant() < 0) {
SetBit(kGeoReflection);
// printf("matrix %s is reflection/n", GetName());
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetInverse(Double_t *invmat) const
{
// Get the inverse rotation matrix (which is simply the transpose)
if (!invmat) {
Error("GetInverse", "no place to store the inverse matrix");
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; i<3; i++) {
invmat[3*i+j] = fRotationMatrix[3*j+i];
}
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MultiplyBy(TGeoRotation *rot, Bool_t after)
{
const Double_t *matleft, *matright;
Double_t newmat[9] = {0};
if (after) {
matleft = &fRotationMatrix[0];
matright = rot->GetRotationMatrix();
} else {
matleft = rot->GetRotationMatrix();
matright = &fRotationMatrix[0];
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; j<3; j++) {
for (Int_t k=0; k<3; k++) {
newmat[3*i+j] += matleft[3*i+k] * matright[3*k+j];
}
}
}
memcpy(&fRotationMatrix[0], &newmat[0], kN9);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale()
{
// default constructor
SetBit(kGeoScale);
for (Int_t i=0; i<3; i++) fScale[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const TGeoScale &other)
:TGeoMatrix()
{
// Copy constructor
SetBit(kGeoScale);
const Double_t *scl = other.GetScale();
memcpy(fScale, scl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix("")
{
// default constructor
SetBit(kGeoScale);
SetDefaultName();
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const char *name, Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix(name)
{
// default constructor
SetBit(kGeoScale);
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::~TGeoScale()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoScale::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t scale[3];
scale[0] = 1./fScale[0];
scale[1] = 1./fScale[1];
scale[2] = 1./fScale[2];
h.SetScale(scale);
return h;
}
//-----------------------------------------------------------------------------
void TGeoScale::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// scale setter
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
Bool_t TGeoScale::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans()
{
// dummy ctor
SetBit(kGeoCombiTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoCombiTrans &other)
:TGeoMatrix()
{
// Copy ctor
SetBit(kGeoCombiTrans);
const Double_t *trans = other.GetTranslation();
const TGeoRotation rot = *other.GetRotation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoTranslation &tr, const TGeoRotation &rot)
{
SetBit(kGeoCombiTrans);
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = new TGeoRotation("");
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix("")
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name, Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::~TGeoCombiTrans()
{
// destructor
if (fRotation) delete fRotation;
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoCombiTrans::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
Double_t newrot[9];
const Double_t *rot = GetRotationMatrix();
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
newrot[0] = rot[0];
newrot[1] = rot[3];
newrot[2] = rot[6];
newrot[3] = rot[1];
newrot[4] = rot[4];
newrot[5] = rot[7];
newrot[6] = rot[2];
newrot[7] = rot[5];
newrot[8] = rot[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
// if (fRotation) fRotation->RegisterYourself();
}
if (!gGeoManager)
Warning("RegisterYourself", "cannot register without geometry");
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateX(Double_t angle)
{
// Combine this with a rotation about X axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateX", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateX(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = fTranslation[0];
tr[1] = c*fTranslation[1]+s*fTranslation[2];
tr[2] = -s*fTranslation[1]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateY(Double_t angle)
{
// Combine this with a rotation about Y axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateY", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateY(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]-s*fTranslation[2];
tr[1] = fTranslation[1];
tr[2] = s*fTranslation[0]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateZ(Double_t angle)
{
// Combine this with a rotation about Z axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateZ", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateZ(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]+s*fTranslation[1];
tr[1] = -s*fTranslation[0]+c*fTranslation[1];
tr[2] = fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(TGeoRotation *rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
const TGeoRotation r = *rot;
fRotation->SetRotation(r);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(const TGeoRotation &rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
fRotation->SetRotation(rot);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(const TGeoTranslation &tr)
{
// copy the translation component
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// set the translation component
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t *vect)
{
// set the translation component
fTranslation[0] = vect[0];
fTranslation[1] = vect[1];
fTranslation[2] = vect[2];
}
//-----------------------------------------------------------------------------
const Double_t *TGeoCombiTrans::GetRotationMatrix() const
{
// get the rotation array
if (!fRotation) return kIdentityMatrix;
return fRotation->GetRotationMatrix();
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans()
{
// dummy ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans("")
{
// ctor
SetBit(kGeoGenTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name, Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::~TGeoGenTrans()
{
// destructor
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::Clear(Option_t *)
{
// clear the fields of this transformation
memset(&fTranslation[0], 0, kN3);
memset(&fScale[0], 0, kN3);
if (fRotation) fRotation->Clear();
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// set the scale
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoGenTrans::Inverse() const
{
// Return a temporary inverse of this.
Error("Inverse", "not implemented");
static TGeoHMatrix h;
h = *this;
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoGenTrans::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity()
{
// dummy ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity(const char *name)
:TGeoMatrix(name)
{
// ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoIdentity::Inverse() const
{
// Return a temporary inverse of this.
return *gGeoIdentity;
}
/*************************************************************************
* TGeoHMatrix - Matrix class used for computing global transformations *
* Should NOT be used for node definition. An instance of this class *
* is generally used to pile-up local transformations starting from *
* the top level physical node, down to the current node. *
*************************************************************************/
ClassImp(TGeoHMatrix)
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix()
{
// dummy ctor
memset(&fTranslation[0], 0, kN3);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
memcpy(fScale,kUnitScale,kN3);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const char* name)
:TGeoMatrix(name)
{
// ctor
memset(&fTranslation[0], 0, kN3);
SetRotation(&kIdentityMatrix[0]);
SetScale(&kUnitScale[0]);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const TGeoMatrix &matrix)
{
// assignment
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
SetTranslation(matrix.GetTranslation());
} else {
memset(&fTranslation[0], 0, kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoHMatrix::~TGeoHMatrix()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix *matrix)
{
// assignment
if (matrix == this) return *this;
Clear();
if (matrix->IsIdentity()) return *this;
if (matrix->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix->GetTranslation(),kN3);
}
if (matrix->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix->GetRotationMatrix(),kN9);
}
if (matrix->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix->GetScale(),kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix &matrix)
{
// assignment
if (&matrix == this) return *this;
if (matrix.IsIdentity()) return *this;
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix.GetTranslation(),kN3);
} else {
memcpy(fTranslation,kNullVector,kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Clear(Option_t *)
{
// clear the data for this matrix
if (IsIdentity()) return;
if (IsTranslation()) {
ResetBit(kGeoTranslation);
memcpy(fTranslation,kNullVector,kN3);
}
if (IsRotation()) {
ResetBit(kGeoRotation);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (IsScale()) {
ResetBit(kGeoScale);
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoHMatrix::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
if (IsTranslation()) {
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
}
if (IsRotation()) {
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
}
if (IsScale()) {
Double_t sc[3];
sc[0] = 1./fScale[0];
sc[1] = 1./fScale[1];
sc[2] = 1./fScale[2];
h.SetScale(sc);
}
return h;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Multiply(const TGeoMatrix *right)
{
// multiply to the right with an other transformation
// if right is identity matrix, just return
if (right == gGeoIdentity) return;
const Double_t *r_tra = right->GetTranslation();
const Double_t *r_rot = right->GetRotationMatrix();
const Double_t *r_scl = right->GetScale();
if (IsIdentity()) {
if (right->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,r_rot,kN9);
}
if (right->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,r_scl,kN3);
}
if (right->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,r_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_rot[9];
if (right->IsRotation()) SetBit(kGeoRotation);
if (right->IsScale()) SetBit(kGeoScale);
if (right->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
fTranslation[i] += fRotationMatrix[3*i]*r_tra[0]
+ fRotationMatrix[3*i+1]*r_tra[1]
+ fRotationMatrix[3*i+2]*r_tra[2];
}
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = fRotationMatrix[3*i]*r_rot[j] +
fRotationMatrix[3*i+1]*r_rot[3+j] +
fRotationMatrix[3*i+2]*r_rot[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= r_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::MultiplyLeft(const TGeoMatrix *left)
{
// multiply to the left with an other transformation
// if right is identity matrix, just return
if (left == gGeoIdentity) return;
const Double_t *l_tra = left->GetTranslation();
const Double_t *l_rot = left->GetRotationMatrix();
const Double_t *l_scl = left->GetScale();
if (IsIdentity()) {
if (left->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,l_rot,kN9);
}
if (left->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,l_scl,kN3);
}
if (left->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,l_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_tra[3];
Double_t new_rot[9];
if (left->IsRotation()) SetBit(kGeoRotation);
if (left->IsScale()) SetBit(kGeoScale);
if (left->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
new_tra[i] = l_tra[i]
+ l_rot[3*i]* fTranslation[0]
+ l_rot[3*i+1]*fTranslation[1]
+ l_rot[3*i+2]*fTranslation[2];
}
memcpy(fTranslation,new_tra,kN3);
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = l_rot[3*i]*fRotationMatrix[j] +
l_rot[3*i+1]*fRotationMatrix[3+j] +
l_rot[3*i+2]*fRotationMatrix[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= l_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = fTranslation[0];
v[1] = c*fTranslation[1]+s*fTranslation[2];
v[2] = -s*fTranslation[1]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]-s*fTranslation[2];
v[1] = fTranslation[1];
v[2] = s*fTranslation[0]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]+s*fTranslation[1];
v[1] = -s*fTranslation[0]+c*fTranslation[1];
v[2] = fTranslation[2];
memcpy(fTranslation,v,kN3);
}
*/
//
//
// The base class TGeoMatrix defines abstract metods for:
//
// - translation, rotation and scale getters. Every derived class stores only
// its specific data, e.g. a translation stores an array of 3 doubles and a
// rotation an array of 9. However, asking which is the rotation array of a
// TGeoTranslation through the base TGeoMatrix interface is a legal operation.
// The answer in this case is a pointer to a global constant array representing
// an identity rotation.
// Double_t *TGeoMatrix::GetTranslation()
// Double_t *TGeoMatrix::GetRotation()
// Double_t *TGeoMatrix::GetScale()
//
// - MasterToLocal() and LocalToMaster() point and vector transformations :
// void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master)
// void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master)
// These allow correct conversion also for reflections.
// - Transformation type getters :
// Bool_t TGeoMatrix::IsIdentity()
// Bool_t TGeoMatrix::IsTranslation()
// Bool_t TGeoMatrix::IsRotation()
// Bool_t TGeoMatrix::IsScale()
// Bool_t TGeoMatrix::IsCombi() (translation + rotation)
// Bool_t TGeoMatrix::IsGeneral() (translation + rotation + scale)
//
// Combinations of basic transformations are represented by specific classes
// deriving from TGeoMatrix. In order to define a matrix as a combination of several
// others, a special class TGeoHMatrix is provided. Here is an example of matrix
// creation :
//
// Matrix creation example:
//
// root[0] TGeoRotation r1,r2;
// r1.SetAngles(90,0,30); // rotation defined by Euler angles
// r2.SetAngles(90,90,90,180,0,0); // rotation defined by GEANT3 angles
// TGeoTranslation t1(-10,10,0);
// TGeoTranslation t2(10,-10,5);
// TGeoCombiTrans c1(t1,r1);
// TGeoCombiTrans c2(t2,r2);
// TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix class
// root[7] TGeoHMatrix *ph = new TGeoHMatrix(hm); // this is the one we want to
// // use for positioning a volume
// root[8] ph->Print();
// ...
// pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by the manager
//
// Rule for matrix creation:
// - unless explicitly used for positioning nodes (TGeoVolume::AddNode()) all
// matrices deletion have to be managed by users. Matrices passed to geometry
// have to be created by using new() operator and their deletion is done by
// TGeoManager class.
//
// Available geometrical transformations
//
// 1. TGeoTranslation - represent a (dx,dy,dz) translation. Data members:
// Double_t fTranslation[3]. Translations can be added/subtracted.
// TGeoTranslation t1;
// t1->SetTranslation(-5,10,4);
// TGeoTranslation *t2 = new TGeoTranslation(4,3,10);
// t2->Subtract(&t1);
//
// 2. Rotations - represent a pure rotation. Data members: Double_t fRotationMatrix[3*3].
// Rotations can be defined either by Euler angles, either, by GEANT3 angles :
// TGeoRotation *r1 = new TGeoRotation();
// r1->SetAngles(phi, theta, psi); // all angles in degrees
// This represent the composition of : first a rotation about Z axis with
// angle phi, then a rotation with theta about the rotated X axis, and
// finally a rotation with psi about the new Z axis.
//
// r1->SetAngles(th1,phi1, th2,phi2, th3,phi3)
// This is a rotation defined in GEANT3 style. Theta and phi are the spherical
// angles of each axis of the rotated coordinate system with respect to the
// initial one. This construction allows definition of malformed rotations,
// e.g. not orthogonal. A check is performed and an error message is issued
// in this case.
//
// Specific utilities : determinant, inverse.
//
// 3. Scale transformations - represent a scale shrinking/enlargement. Data
// members :Double_t fScale[3]. Not fully implemented yet.
//
// 4. Combined transformations - represent a rotation folowed by a translation.
// Data members: Double_t fTranslation[3], TGeoRotation *fRotation.
// TGeoRotation *rot = new TGeoRotation("rot",10,20,30);
// TGeoTranslation trans;
// ...
// TGeoCombiTrans *c1 = new TGeoCombiTrans(trans, rot);
// TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot)
//
// 5. TGeoGenTrans - combined transformations including a scale. Not implemented.
// 6. TGeoIdentity - a generic singleton matrix representing a identity transformation
// NOTE: identified by the global variable gGeoIdentity.
//
//
#include "TObjArray.h"
#include "TGeoManager.h"
#include "TGeoMatrix.h"
TGeoIdentity *gGeoIdentity = 0;
const Int_t kN3 = 3*sizeof(Double_t);
const Int_t kN9 = 9*sizeof(Double_t);
// statics and globals
ClassImp(TGeoMatrix)
ClassImp(TGeoTranslation)
ClassImp(TGeoRotation)
ClassImp(TGeoScale)
ClassImp(TGeoCombiTrans)
ClassImp(TGeoGenTrans)
ClassImp(TGeoIdentity)
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix()
{
// dummy constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix(const char *name)
:TNamed(name, "")
{
// Constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::~TGeoMatrix()
{
// Destructor
if (IsRegistered() && gGeoManager) {
if (gGeoManager->GetListOfVolumes()) {
gGeoManager->GetListOfMatrices()->Remove(this);
Error("dtor", "a registered matrix was removed !!!");
}
}
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoMatrix::operator*(const TGeoMatrix &right) const
{
// Multiplication
static TGeoHMatrix h;
h = *this;
h.Multiply(&right);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoMatrix::IsRotAboutZ() const
{
// Returns true if no rotation or the rotation is about Z axis
if (IsIdentity()) return kTRUE;
const Double_t *rot = GetRotationMatrix();
if (TMath::Abs(rot[6])>1E-9) return kFALSE;
if (TMath::Abs(rot[7])>1E-9) return kFALSE;
if ((1.-TMath::Abs(rot[8]))>1E-9) return kFALSE;
return kTRUE;
}
//-----------------------------------------------------------------------------
Int_t TGeoMatrix::GetByteCount() const
{
// Get total size in bytes of this
Int_t count = 4+28+strlen(GetName())+strlen(GetTitle()); // fId + TNamed
if (IsTranslation()) count += 12;
if (IsScale()) count += 12;
if (IsCombi() || IsGeneral()) count += 4 + 36;
return count;
}
//-----------------------------------------------------------------------------
void TGeoMatrix::GetHomogenousMatrix(Double_t *hmat) const
{
// The homogenous matrix associated with the transformation is used for
// piling up's and visualization. A homogenous matrix is a 4*4 array
// containing the translation, the rotation and the scale components
//
// | R00*sx R01 R02 dx |
// | R10 R11*sy R12 dy |
// | R20 R21 R22*sz dz |
// | 0 0 0 1 |
//
// where Rij is the rotation matrix, (sx, sy, sz) is the scale
// transformation and (dx, dy, dz) is the translation.
Double_t *hmatrix = hmat;
const Double_t *mat = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
memcpy(hmatrix, mat, kN3);
mat += 3;
hmatrix += 3;
*hmatrix = 0.0;
hmatrix++;
}
memcpy(hmatrix, GetTranslation(), kN3);
hmatrix = hmat;
if (IsScale()) {
for (Int_t i=0; i<3; i++) {
*hmatrix *= GetScale()[i];
hmatrix += 5;
}
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = tr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = bombtr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
Double_t mt0 = master[0]-tr[0];
Double_t mt1 = master[1]-tr[1];
Double_t mt2 = master[2]-tr[2];
local[0] = mt0*rot[0] + mt1*rot[3] + mt2*rot[6];
local[1] = mt0*rot[1] + mt1*rot[4] + mt2*rot[7];
local[2] = mt0*rot[2] + mt1*rot[5] + mt2*rot[8];
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = (master[0]-bombtr[0])*rot[i]
+ (master[1]-bombtr[1])*rot[i+3]
+ (master[2]-bombtr[2])*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::Print(Option_t *) const
{
// print the matrix in 4x4 format
const Double_t *rot = GetRotationMatrix();
const Double_t *tr = GetTranslation();
const Double_t *sc = GetScale();
printf("matrix %s - translation : %i rotation : %i scale : %in", GetName(),(Int_t)IsTranslation(),
(Int_t)IsRotation(), (Int_t)IsScale());
printf(" %g %g %g %gn", rot[0], rot[1], rot[2], (Double_t)0);
printf(" %g %g %g %gn", rot[3], rot[4], rot[5], (Double_t)0);
printf(" %g %g %g %gn", rot[6], rot[7], rot[8], (Double_t)0);
printf(" %g %g %g %gn", tr[0], tr[1], tr[2], (Double_t)1);
if (IsScale()) printf("Scale : %g %g %gn", sc[0], sc[1], sc[2]);
}
//-----------------------------------------------------------------------------
void TGeoMatrix::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::SetDefaultName()
{
// If no name was supplied in the ctor, the type of transformation is checked.
// A letter will be prepended to the name :
// t - translation
// r - rotation
// s - scale
// c - combi (translation + rotation)
// g - general (tr+rot+scale)
// The index of the transformation in gGeoManager list of transformations will
// be appended.
if (!gGeoManager) return;
if (strlen(GetName())) return;
char type = 'n';
if (IsTranslation()) type = 't';
if (IsRotation()) type = 'r';
if (IsScale()) type = 's';
if (IsCombi()) type = 'c';
if (IsGeneral()) type = 'g';
TObjArray *matrices = gGeoManager->GetListOfMatrices();
Int_t index = 0;
if (matrices) index =matrices->GetEntriesFast() - 1;
Int_t digits = 1;
Int_t num = 10;
while ((Int_t)(index/num)) {
digits++;
num *= 10;
}
char *name = new char[digits+2];
sprintf(name, "%c%i", type, index);
SetName(name);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation()
{
// Default constructor
SetBit(kGeoTranslation);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const TGeoTranslation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoTranslation);
const Double_t *transl = other.GetTranslation();
memcpy(fTranslation, transl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix("")
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetDefaultName();
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const char *name, Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix(name)
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoTranslation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
return h;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Add(const TGeoTranslation *other)
{
// Adding a translation to this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] += trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Subtract(const TGeoTranslation *other)
{
// Subtracting a translation from this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] -= trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// Set translation components
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
master[i] = tr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector to MARS
memcpy(master, local, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
master[i] = bombtr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
local[i] = master[i]-tr[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a vector from MARS to local
memcpy(local, master, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
local[i] = master[i]-bombtr[i];
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation()
{
// Default constructor.
SetBit(kGeoRotation);
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const TGeoRotation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoRotation);
SetRotation(other);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name)
:TGeoMatrix(name)
{
// Named rotation constructor
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
SetBit(kGeoRotation);
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t phi, Double_t theta, Double_t psi)
:TGeoMatrix(name)
{
// Default rotation constructor with Euler angles. Phi is the rotation angle about
// Z axis and is done first, theta is the rotation about new Y and is done
// second, psi is the rotation angle about new Z and is done third. All angles are in
// degrees.
SetBit(kGeoRotation);
SetAngles(phi, theta, psi);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
:TGeoMatrix(name)
{
// Rotation constructor a la GEANT3. Angles theta(i), phi(i) are the polar and azimuthal
// angles of the (i) axis of the rotated system with respect to the initial non-rotated
// system.
// Example : the identity matrix (no rotation) is composed by
// theta1=90, phi1=0, theta2=90, phi2=90, theta3=0, phi3=0
SetBit(kGeoRotation);
SetAngles(theta1, phi1, theta2, phi2, theta3, phi3);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoRotation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoRotation::IsValid() const
{
// Perform orthogonality test for rotation.
const Double_t *r = fRotationMatrix;
Double_t cij;
for (Int_t i=0; i<2; i++) {
for (Int_t j=i+1; j<3; j++) {
// check columns
cij = TMath::Abs(r[i]*r[j]+r[i+3]*r[j+3]+r[i+6]*r[j+6]);
if (cij>1E-4) return kFALSE;
// check rows
cij = TMath::Abs(r[3*i]*r[3*j]+r[3*i+1]*r[3*j+1]+r[3*i+2]*r[3*j+2]);
if (cij>1E-4) return kFALSE;
}
}
return kTRUE;
}
//-----------------------------------------------------------------------------
void TGeoRotation::Clear(Option_t *)
{
// reset data members to 0
memset(&fRotationMatrix[0], 0, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::FastRotZ(Double_t *sincos)
{
fRotationMatrix[0] = sincos[1];
fRotationMatrix[1] = -sincos[0];
fRotationMatrix[3] = sincos[0];
fRotationMatrix[4] = sincos[1];
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::GetPhiRotation() const
{
//--- Returns rotation angle about Z axis in degrees.
Double_t phi = 180.*TMath::ATan2(fRotationMatrix[1], fRotationMatrix[0])/TMath::Pi();
return phi;
}
//-----------------------------------------------------------------------------
void TGeoRotation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetRotation(const TGeoRotation &other)
{
// Copy rotation elements from other rotation matrix.
const Double_t *rot = other.GetRotationMatrix();
memcpy(fRotationMatrix, rot, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t phi, Double_t theta, Double_t psi)
{
// Set matrix elements according to Euler angles
Double_t degrad = TMath::Pi()/180.;
Double_t sinphi = TMath::Sin(degrad*phi);
Double_t cosphi = TMath::Cos(degrad*phi);
Double_t sinthe = TMath::Sin(degrad*theta);
Double_t costhe = TMath::Cos(degrad*theta);
Double_t sinpsi = TMath::Sin(degrad*psi);
Double_t cospsi = TMath::Cos(degrad*psi);
fRotationMatrix[0] = cospsi*cosphi - costhe*sinphi*sinpsi;
fRotationMatrix[1] = -sinpsi*cosphi - costhe*sinphi*cospsi;
fRotationMatrix[2] = sinthe*sinphi;
fRotationMatrix[3] = cospsi*sinphi + costhe*cosphi*sinpsi;
fRotationMatrix[4] = -sinpsi*sinphi + costhe*cosphi*cospsi;
fRotationMatrix[5] = -sinthe*cosphi;
fRotationMatrix[6] = sinpsi*sinthe;
fRotationMatrix[7] = cospsi*sinthe;
fRotationMatrix[8] = costhe;
if (!IsValid()) Error("SetAngles", "invalid rotation (Euler angles : phi=%f theta=%f psi=%f)",phi,theta,psi);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
{
// Set matrix elements in the GEANT3 way
Double_t degrad = TMath::Pi()/180.;
fRotationMatrix[0] = TMath::Cos(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[3] = TMath::Sin(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[6] = TMath::Cos(degrad*theta1);
fRotationMatrix[1] = TMath::Cos(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[4] = TMath::Sin(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[7] = TMath::Cos(degrad*theta2);
fRotationMatrix[2] = TMath::Cos(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[5] = TMath::Sin(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[8] = TMath::Cos(degrad*theta3);
// do the trick to eliminate most of the floating point errors
for (Int_t i=0; i<9; i++) {
if (TMath::Abs(fRotationMatrix[i])<1E-15) fRotationMatrix[i] = 0;
if (TMath::Abs(fRotationMatrix[i]-1)<1E-15) fRotationMatrix[i] = 1;
if (TMath::Abs(fRotationMatrix[i]+1)<1E-15) fRotationMatrix[i] = -1;
}
if (!IsValid()) Error("SetAngles", "invalid rotation (G3 angles, th1=%f phi1=%f, th2=%f ph2=%f, th3=%f phi3=%f)",
theta1,phi1,theta2,phi2,theta3,phi3);
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetAngles(Double_t &theta1, Double_t &phi1, Double_t &theta2, Double_t &phi2,
Double_t &theta3, Double_t &phi3) const
{
// Retreive rotation angles
Double_t raddeg = 180./TMath::Pi();
theta1 = raddeg*TMath::ACos(fRotationMatrix[6]);
theta2 = raddeg*TMath::ACos(fRotationMatrix[7]);
theta3 = raddeg*TMath::ACos(fRotationMatrix[8]);
if (TMath::Abs(fRotationMatrix[0])<1E-6 && TMath::Abs(fRotationMatrix[3])<1E-6) phi1=0.;
else phi1 = raddeg*TMath::ATan2(fRotationMatrix[3],fRotationMatrix[0]);
if (phi1<0) phi1+=360.;
if (TMath::Abs(fRotationMatrix[1])<1E-6 && TMath::Abs(fRotationMatrix[4])<1E-6) phi2=0.;
else phi2 = raddeg*TMath::ATan2(fRotationMatrix[4],fRotationMatrix[1]);
if (phi2<0) phi2+=360.;
if (TMath::Abs(fRotationMatrix[2])<1E-6 && TMath::Abs(fRotationMatrix[5])<1E-6) phi3=0.;
else phi3 = raddeg*TMath::ATan2(fRotationMatrix[5],fRotationMatrix[2]);
if (phi3<0) phi3+=360.;
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::Determinant() const
{
// computes determinant of the rotation matrix
Double_t
det = fRotationMatrix[0]*fRotationMatrix[4]*fRotationMatrix[8] +
fRotationMatrix[3]*fRotationMatrix[7]*fRotationMatrix[1] +
fRotationMatrix[6]*fRotationMatrix[1]*fRotationMatrix[5] -
fRotationMatrix[2]*fRotationMatrix[4]*fRotationMatrix[6] -
fRotationMatrix[5]*fRotationMatrix[7]*fRotationMatrix[0] -
fRotationMatrix[7]*fRotationMatrix[1]*fRotationMatrix[3];
return det;
}
//-----------------------------------------------------------------------------
void TGeoRotation::CheckMatrix()
{
// performes an orthogonality check and finds if the matrix is a reflection
// Warning("CheckMatrix", "orthogonality check not performed yet");
if (Determinant() < 0) {
SetBit(kGeoReflection);
// printf("matrix %s is reflection/n", GetName());
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetInverse(Double_t *invmat) const
{
// Get the inverse rotation matrix (which is simply the transpose)
if (!invmat) {
Error("GetInverse", "no place to store the inverse matrix");
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; i<3; i++) {
invmat[3*i+j] = fRotationMatrix[3*j+i];
}
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MultiplyBy(TGeoRotation *rot, Bool_t after)
{
const Double_t *matleft, *matright;
Double_t newmat[9] = {0};
if (after) {
matleft = &fRotationMatrix[0];
matright = rot->GetRotationMatrix();
} else {
matleft = rot->GetRotationMatrix();
matright = &fRotationMatrix[0];
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; j<3; j++) {
for (Int_t k=0; k<3; k++) {
newmat[3*i+j] += matleft[3*i+k] * matright[3*k+j];
}
}
}
memcpy(&fRotationMatrix[0], &newmat[0], kN9);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale()
{
// default constructor
SetBit(kGeoScale);
for (Int_t i=0; i<3; i++) fScale[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const TGeoScale &other)
:TGeoMatrix()
{
// Copy constructor
SetBit(kGeoScale);
const Double_t *scl = other.GetScale();
memcpy(fScale, scl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix("")
{
// default constructor
SetBit(kGeoScale);
SetDefaultName();
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const char *name, Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix(name)
{
// default constructor
SetBit(kGeoScale);
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::~TGeoScale()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoScale::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t scale[3];
scale[0] = 1./fScale[0];
scale[1] = 1./fScale[1];
scale[2] = 1./fScale[2];
h.SetScale(scale);
return h;
}
//-----------------------------------------------------------------------------
void TGeoScale::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// scale setter
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
Bool_t TGeoScale::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans()
{
// dummy ctor
SetBit(kGeoCombiTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoCombiTrans &other)
:TGeoMatrix()
{
// Copy ctor
SetBit(kGeoCombiTrans);
const Double_t *trans = other.GetTranslation();
const TGeoRotation rot = *other.GetRotation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoTranslation &tr, const TGeoRotation &rot)
{
SetBit(kGeoCombiTrans);
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = new TGeoRotation("");
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix("")
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name, Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::~TGeoCombiTrans()
{
// destructor
if (fRotation) delete fRotation;
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoCombiTrans::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
Double_t newrot[9];
const Double_t *rot = GetRotationMatrix();
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
newrot[0] = rot[0];
newrot[1] = rot[3];
newrot[2] = rot[6];
newrot[3] = rot[1];
newrot[4] = rot[4];
newrot[5] = rot[7];
newrot[6] = rot[2];
newrot[7] = rot[5];
newrot[8] = rot[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
// if (fRotation) fRotation->RegisterYourself();
}
if (!gGeoManager)
Warning("RegisterYourself", "cannot register without geometry");
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateX(Double_t angle)
{
// Combine this with a rotation about X axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateX", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateX(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = fTranslation[0];
tr[1] = c*fTranslation[1]+s*fTranslation[2];
tr[2] = -s*fTranslation[1]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateY(Double_t angle)
{
// Combine this with a rotation about Y axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateY", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateY(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]-s*fTranslation[2];
tr[1] = fTranslation[1];
tr[2] = s*fTranslation[0]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateZ(Double_t angle)
{
// Combine this with a rotation about Z axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateZ", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateZ(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]+s*fTranslation[1];
tr[1] = -s*fTranslation[0]+c*fTranslation[1];
tr[2] = fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(TGeoRotation *rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
const TGeoRotation r = *rot;
fRotation->SetRotation(r);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(const TGeoRotation &rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
fRotation->SetRotation(rot);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(const TGeoTranslation &tr)
{
// copy the translation component
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// set the translation component
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t *vect)
{
// set the translation component
fTranslation[0] = vect[0];
fTranslation[1] = vect[1];
fTranslation[2] = vect[2];
}
//-----------------------------------------------------------------------------
const Double_t *TGeoCombiTrans::GetRotationMatrix() const
{
// get the rotation array
if (!fRotation) return kIdentityMatrix;
return fRotation->GetRotationMatrix();
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans()
{
// dummy ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans("")
{
// ctor
SetBit(kGeoGenTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name, Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::~TGeoGenTrans()
{
// destructor
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::Clear(Option_t *)
{
// clear the fields of this transformation
memset(&fTranslation[0], 0, kN3);
memset(&fScale[0], 0, kN3);
if (fRotation) fRotation->Clear();
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// set the scale
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoGenTrans::Inverse() const
{
// Return a temporary inverse of this.
Error("Inverse", "not implemented");
static TGeoHMatrix h;
h = *this;
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoGenTrans::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity()
{
// dummy ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity(const char *name)
:TGeoMatrix(name)
{
// ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoIdentity::Inverse() const
{
// Return a temporary inverse of this.
return *gGeoIdentity;
}
/*************************************************************************
* TGeoHMatrix - Matrix class used for computing global transformations *
* Should NOT be used for node definition. An instance of this class *
* is generally used to pile-up local transformations starting from *
* the top level physical node, down to the current node. *
*************************************************************************/
ClassImp(TGeoHMatrix)
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix()
{
// dummy ctor
memset(&fTranslation[0], 0, kN3);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
memcpy(fScale,kUnitScale,kN3);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const char* name)
:TGeoMatrix(name)
{
// ctor
memset(&fTranslation[0], 0, kN3);
SetRotation(&kIdentityMatrix[0]);
SetScale(&kUnitScale[0]);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const TGeoMatrix &matrix)
{
// assignment
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
SetTranslation(matrix.GetTranslation());
} else {
memset(&fTranslation[0], 0, kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoHMatrix::~TGeoHMatrix()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix *matrix)
{
// assignment
if (matrix == this) return *this;
Clear();
if (matrix->IsIdentity()) return *this;
if (matrix->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix->GetTranslation(),kN3);
}
if (matrix->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix->GetRotationMatrix(),kN9);
}
if (matrix->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix->GetScale(),kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix &matrix)
{
// assignment
if (&matrix == this) return *this;
if (matrix.IsIdentity()) return *this;
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix.GetTranslation(),kN3);
} else {
memcpy(fTranslation,kNullVector,kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Clear(Option_t *)
{
// clear the data for this matrix
if (IsIdentity()) return;
if (IsTranslation()) {
ResetBit(kGeoTranslation);
memcpy(fTranslation,kNullVector,kN3);
}
if (IsRotation()) {
ResetBit(kGeoRotation);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (IsScale()) {
ResetBit(kGeoScale);
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoHMatrix::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
if (IsTranslation()) {
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
}
if (IsRotation()) {
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
}
if (IsScale()) {
Double_t sc[3];
sc[0] = 1./fScale[0];
sc[1] = 1./fScale[1];
sc[2] = 1./fScale[2];
h.SetScale(sc);
}
return h;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Multiply(const TGeoMatrix *right)
{
// multiply to the right with an other transformation
// if right is identity matrix, just return
if (right == gGeoIdentity) return;
const Double_t *r_tra = right->GetTranslation();
const Double_t *r_rot = right->GetRotationMatrix();
const Double_t *r_scl = right->GetScale();
if (IsIdentity()) {
if (right->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,r_rot,kN9);
}
if (right->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,r_scl,kN3);
}
if (right->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,r_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_rot[9];
if (right->IsRotation()) SetBit(kGeoRotation);
if (right->IsScale()) SetBit(kGeoScale);
if (right->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
fTranslation[i] += fRotationMatrix[3*i]*r_tra[0]
+ fRotationMatrix[3*i+1]*r_tra[1]
+ fRotationMatrix[3*i+2]*r_tra[2];
}
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = fRotationMatrix[3*i]*r_rot[j] +
fRotationMatrix[3*i+1]*r_rot[3+j] +
fRotationMatrix[3*i+2]*r_rot[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= r_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::MultiplyLeft(const TGeoMatrix *left)
{
// multiply to the left with an other transformation
// if right is identity matrix, just return
if (left == gGeoIdentity) return;
const Double_t *l_tra = left->GetTranslation();
const Double_t *l_rot = left->GetRotationMatrix();
const Double_t *l_scl = left->GetScale();
if (IsIdentity()) {
if (left->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,l_rot,kN9);
}
if (left->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,l_scl,kN3);
}
if (left->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,l_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_tra[3];
Double_t new_rot[9];
if (left->IsRotation()) SetBit(kGeoRotation);
if (left->IsScale()) SetBit(kGeoScale);
if (left->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
new_tra[i] = l_tra[i]
+ l_rot[3*i]* fTranslation[0]
+ l_rot[3*i+1]*fTranslation[1]
+ l_rot[3*i+2]*fTranslation[2];
}
memcpy(fTranslation,new_tra,kN3);
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = l_rot[3*i]*fRotationMatrix[j] +
l_rot[3*i+1]*fRotationMatrix[3+j] +
l_rot[3*i+2]*fRotationMatrix[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= l_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = fTranslation[0];
v[1] = c*fTranslation[1]+s*fTranslation[2];
v[2] = -s*fTranslation[1]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]-s*fTranslation[2];
v[1] = fTranslation[1];
v[2] = s*fTranslation[0]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]+s*fTranslation[1];
v[1] = -s*fTranslation[0]+c*fTranslation[1];
v[2] = fTranslation[2];
memcpy(fTranslation,v,kN3);
}
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
//
//
// The base class TGeoMatrix defines abstract metods for:
//
// - translation, rotation and scale getters. Every derived class stores only
// its specific data, e.g. a translation stores an array of 3 doubles and a
// rotation an array of 9. However, asking which is the rotation array of a
// TGeoTranslation through the base TGeoMatrix interface is a legal operation.
// The answer in this case is a pointer to a global constant array representing
// an identity rotation.
// Double_t *TGeoMatrix::GetTranslation()
// Double_t *TGeoMatrix::GetRotation()
// Double_t *TGeoMatrix::GetScale()
//
// - MasterToLocal() and LocalToMaster() point and vector transformations :
// void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master)
// void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master)
// These allow correct conversion also for reflections.
// - Transformation type getters :
// Bool_t TGeoMatrix::IsIdentity()
// Bool_t TGeoMatrix::IsTranslation()
// Bool_t TGeoMatrix::IsRotation()
// Bool_t TGeoMatrix::IsScale()
// Bool_t TGeoMatrix::IsCombi() (translation + rotation)
// Bool_t TGeoMatrix::IsGeneral() (translation + rotation + scale)
//
// Combinations of basic transformations are represented by specific classes
// deriving from TGeoMatrix. In order to define a matrix as a combination of several
// others, a special class TGeoHMatrix is provided. Here is an example of matrix
// creation :
//
// Matrix creation example:
//
// root[0] TGeoRotation r1,r2;
// r1.SetAngles(90,0,30); // rotation defined by Euler angles
// r2.SetAngles(90,90,90,180,0,0); // rotation defined by GEANT3 angles
// TGeoTranslation t1(-10,10,0);
// TGeoTranslation t2(10,-10,5);
// TGeoCombiTrans c1(t1,r1);
// TGeoCombiTrans c2(t2,r2);
// TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix class
// root[7] TGeoHMatrix *ph = new TGeoHMatrix(hm); // this is the one we want to
// // use for positioning a volume
// root[8] ph->Print();
// ...
// pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by the manager
//
// Rule for matrix creation:
// - unless explicitly used for positioning nodes (TGeoVolume::AddNode()) all
// matrices deletion have to be managed by users. Matrices passed to geometry
// have to be created by using new() operator and their deletion is done by
// TGeoManager class.
//
// Available geometrical transformations
//
// 1. TGeoTranslation - represent a (dx,dy,dz) translation. Data members:
// Double_t fTranslation[3]. Translations can be added/subtracted.
// TGeoTranslation t1;
// t1->SetTranslation(-5,10,4);
// TGeoTranslation *t2 = new TGeoTranslation(4,3,10);
// t2->Subtract(&t1);
//
// 2. Rotations - represent a pure rotation. Data members: Double_t fRotationMatrix[3*3].
// Rotations can be defined either by Euler angles, either, by GEANT3 angles :
// TGeoRotation *r1 = new TGeoRotation();
// r1->SetAngles(phi, theta, psi); // all angles in degrees
// This represent the composition of : first a rotation about Z axis with
// angle phi, then a rotation with theta about the rotated X axis, and
// finally a rotation with psi about the new Z axis.
//
// r1->SetAngles(th1,phi1, th2,phi2, th3,phi3)
// This is a rotation defined in GEANT3 style. Theta and phi are the spherical
// angles of each axis of the rotated coordinate system with respect to the
// initial one. This construction allows definition of malformed rotations,
// e.g. not orthogonal. A check is performed and an error message is issued
// in this case.
//
// Specific utilities : determinant, inverse.
//
// 3. Scale transformations - represent a scale shrinking/enlargement. Data
// members :Double_t fScale[3]. Not fully implemented yet.
//
// 4. Combined transformations - represent a rotation folowed by a translation.
// Data members: Double_t fTranslation[3], TGeoRotation *fRotation.
// TGeoRotation *rot = new TGeoRotation("rot",10,20,30);
// TGeoTranslation trans;
// ...
// TGeoCombiTrans *c1 = new TGeoCombiTrans(trans, rot);
// TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot)
//
// 5. TGeoGenTrans - combined transformations including a scale. Not implemented.
// 6. TGeoIdentity - a generic singleton matrix representing a identity transformation
// NOTE: identified by the global variable gGeoIdentity.
//
//
#include "TObjArray.h"
#include "TGeoManager.h"
#include "TGeoMatrix.h"
TGeoIdentity *gGeoIdentity = 0;
const Int_t kN3 = 3*sizeof(Double_t);
const Int_t kN9 = 9*sizeof(Double_t);
// statics and globals
ClassImp(TGeoMatrix)
ClassImp(TGeoTranslation)
ClassImp(TGeoRotation)
ClassImp(TGeoScale)
ClassImp(TGeoCombiTrans)
ClassImp(TGeoGenTrans)
ClassImp(TGeoIdentity)
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix()
{
// dummy constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix(const char *name)
:TNamed(name, "")
{
// Constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::~TGeoMatrix()
{
// Destructor
if (IsRegistered() && gGeoManager) {
if (gGeoManager->GetListOfVolumes()) {
gGeoManager->GetListOfMatrices()->Remove(this);
Error("dtor", "a registered matrix was removed !!!");
}
}
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoMatrix::operator*(const TGeoMatrix &right) const
{
// Multiplication
static TGeoHMatrix h;
h = *this;
h.Multiply(&right);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoMatrix::IsRotAboutZ() const
{
// Returns true if no rotation or the rotation is about Z axis
if (IsIdentity()) return kTRUE;
const Double_t *rot = GetRotationMatrix();
if (TMath::Abs(rot[6])>1E-9) return kFALSE;
if (TMath::Abs(rot[7])>1E-9) return kFALSE;
if ((1.-TMath::Abs(rot[8]))>1E-9) return kFALSE;
return kTRUE;
}
//-----------------------------------------------------------------------------
Int_t TGeoMatrix::GetByteCount() const
{
// Get total size in bytes of this
Int_t count = 4+28+strlen(GetName())+strlen(GetTitle()); // fId + TNamed
if (IsTranslation()) count += 12;
if (IsScale()) count += 12;
if (IsCombi() || IsGeneral()) count += 4 + 36;
return count;
}
//-----------------------------------------------------------------------------
void TGeoMatrix::GetHomogenousMatrix(Double_t *hmat) const
{
// The homogenous matrix associated with the transformation is used for
// piling up's and visualization. A homogenous matrix is a 4*4 array
// containing the translation, the rotation and the scale components
//
// | R00*sx R01 R02 dx |
// | R10 R11*sy R12 dy |
// | R20 R21 R22*sz dz |
// | 0 0 0 1 |
//
// where Rij is the rotation matrix, (sx, sy, sz) is the scale
// transformation and (dx, dy, dz) is the translation.
Double_t *hmatrix = hmat;
const Double_t *mat = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
memcpy(hmatrix, mat, kN3);
mat += 3;
hmatrix += 3;
*hmatrix = 0.0;
hmatrix++;
}
memcpy(hmatrix, GetTranslation(), kN3);
hmatrix = hmat;
if (IsScale()) {
for (Int_t i=0; i<3; i++) {
*hmatrix *= GetScale()[i];
hmatrix += 5;
}
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = tr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = bombtr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
Double_t mt0 = master[0]-tr[0];
Double_t mt1 = master[1]-tr[1];
Double_t mt2 = master[2]-tr[2];
local[0] = mt0*rot[0] + mt1*rot[3] + mt2*rot[6];
local[1] = mt0*rot[1] + mt1*rot[4] + mt2*rot[7];
local[2] = mt0*rot[2] + mt1*rot[5] + mt2*rot[8];
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = (master[0]-bombtr[0])*rot[i]
+ (master[1]-bombtr[1])*rot[i+3]
+ (master[2]-bombtr[2])*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::Print(Option_t *) const
{
// print the matrix in 4x4 format
const Double_t *rot = GetRotationMatrix();
const Double_t *tr = GetTranslation();
const Double_t *sc = GetScale();
printf("matrix %s - translation : %i rotation : %i scale : %in", GetName(),(Int_t)IsTranslation(),
(Int_t)IsRotation(), (Int_t)IsScale());
printf(" %g %g %g %gn", rot[0], rot[1], rot[2], (Double_t)0);
printf(" %g %g %g %gn", rot[3], rot[4], rot[5], (Double_t)0);
printf(" %g %g %g %gn", rot[6], rot[7], rot[8], (Double_t)0);
printf(" %g %g %g %gn", tr[0], tr[1], tr[2], (Double_t)1);
if (IsScale()) printf("Scale : %g %g %gn", sc[0], sc[1], sc[2]);
}
//-----------------------------------------------------------------------------
void TGeoMatrix::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::SetDefaultName()
{
// If no name was supplied in the ctor, the type of transformation is checked.
// A letter will be prepended to the name :
// t - translation
// r - rotation
// s - scale
// c - combi (translation + rotation)
// g - general (tr+rot+scale)
// The index of the transformation in gGeoManager list of transformations will
// be appended.
if (!gGeoManager) return;
if (strlen(GetName())) return;
char type = 'n';
if (IsTranslation()) type = 't';
if (IsRotation()) type = 'r';
if (IsScale()) type = 's';
if (IsCombi()) type = 'c';
if (IsGeneral()) type = 'g';
TObjArray *matrices = gGeoManager->GetListOfMatrices();
Int_t index = 0;
if (matrices) index =matrices->GetEntriesFast() - 1;
Int_t digits = 1;
Int_t num = 10;
while ((Int_t)(index/num)) {
digits++;
num *= 10;
}
char *name = new char[digits+2];
sprintf(name, "%c%i", type, index);
SetName(name);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation()
{
// Default constructor
SetBit(kGeoTranslation);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const TGeoTranslation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoTranslation);
const Double_t *transl = other.GetTranslation();
memcpy(fTranslation, transl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix("")
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetDefaultName();
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const char *name, Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix(name)
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoTranslation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
return h;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Add(const TGeoTranslation *other)
{
// Adding a translation to this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] += trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Subtract(const TGeoTranslation *other)
{
// Subtracting a translation from this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] -= trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// Set translation components
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
master[i] = tr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector to MARS
memcpy(master, local, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
master[i] = bombtr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
local[i] = master[i]-tr[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a vector from MARS to local
memcpy(local, master, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
local[i] = master[i]-bombtr[i];
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation()
{
// Default constructor.
SetBit(kGeoRotation);
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const TGeoRotation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoRotation);
SetRotation(other);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name)
:TGeoMatrix(name)
{
// Named rotation constructor
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
SetBit(kGeoRotation);
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t phi, Double_t theta, Double_t psi)
:TGeoMatrix(name)
{
// Default rotation constructor with Euler angles. Phi is the rotation angle about
// Z axis and is done first, theta is the rotation about new Y and is done
// second, psi is the rotation angle about new Z and is done third. All angles are in
// degrees.
SetBit(kGeoRotation);
SetAngles(phi, theta, psi);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
:TGeoMatrix(name)
{
// Rotation constructor a la GEANT3. Angles theta(i), phi(i) are the polar and azimuthal
// angles of the (i) axis of the rotated system with respect to the initial non-rotated
// system.
// Example : the identity matrix (no rotation) is composed by
// theta1=90, phi1=0, theta2=90, phi2=90, theta3=0, phi3=0
SetBit(kGeoRotation);
SetAngles(theta1, phi1, theta2, phi2, theta3, phi3);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoRotation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoRotation::IsValid() const
{
// Perform orthogonality test for rotation.
const Double_t *r = fRotationMatrix;
Double_t cij;
for (Int_t i=0; i<2; i++) {
for (Int_t j=i+1; j<3; j++) {
// check columns
cij = TMath::Abs(r[i]*r[j]+r[i+3]*r[j+3]+r[i+6]*r[j+6]);
if (cij>1E-4) return kFALSE;
// check rows
cij = TMath::Abs(r[3*i]*r[3*j]+r[3*i+1]*r[3*j+1]+r[3*i+2]*r[3*j+2]);
if (cij>1E-4) return kFALSE;
}
}
return kTRUE;
}
//-----------------------------------------------------------------------------
void TGeoRotation::Clear(Option_t *)
{
// reset data members to 0
memset(&fRotationMatrix[0], 0, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::FastRotZ(Double_t *sincos)
{
fRotationMatrix[0] = sincos[1];
fRotationMatrix[1] = -sincos[0];
fRotationMatrix[3] = sincos[0];
fRotationMatrix[4] = sincos[1];
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::GetPhiRotation() const
{
//--- Returns rotation angle about Z axis in degrees.
Double_t phi = 180.*TMath::ATan2(fRotationMatrix[1], fRotationMatrix[0])/TMath::Pi();
return phi;
}
//-----------------------------------------------------------------------------
void TGeoRotation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetRotation(const TGeoRotation &other)
{
// Copy rotation elements from other rotation matrix.
const Double_t *rot = other.GetRotationMatrix();
memcpy(fRotationMatrix, rot, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t phi, Double_t theta, Double_t psi)
{
// Set matrix elements according to Euler angles
Double_t degrad = TMath::Pi()/180.;
Double_t sinphi = TMath::Sin(degrad*phi);
Double_t cosphi = TMath::Cos(degrad*phi);
Double_t sinthe = TMath::Sin(degrad*theta);
Double_t costhe = TMath::Cos(degrad*theta);
Double_t sinpsi = TMath::Sin(degrad*psi);
Double_t cospsi = TMath::Cos(degrad*psi);
fRotationMatrix[0] = cospsi*cosphi - costhe*sinphi*sinpsi;
fRotationMatrix[1] = -sinpsi*cosphi - costhe*sinphi*cospsi;
fRotationMatrix[2] = sinthe*sinphi;
fRotationMatrix[3] = cospsi*sinphi + costhe*cosphi*sinpsi;
fRotationMatrix[4] = -sinpsi*sinphi + costhe*cosphi*cospsi;
fRotationMatrix[5] = -sinthe*cosphi;
fRotationMatrix[6] = sinpsi*sinthe;
fRotationMatrix[7] = cospsi*sinthe;
fRotationMatrix[8] = costhe;
if (!IsValid()) Error("SetAngles", "invalid rotation (Euler angles : phi=%f theta=%f psi=%f)",phi,theta,psi);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
{
// Set matrix elements in the GEANT3 way
Double_t degrad = TMath::Pi()/180.;
fRotationMatrix[0] = TMath::Cos(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[3] = TMath::Sin(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[6] = TMath::Cos(degrad*theta1);
fRotationMatrix[1] = TMath::Cos(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[4] = TMath::Sin(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[7] = TMath::Cos(degrad*theta2);
fRotationMatrix[2] = TMath::Cos(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[5] = TMath::Sin(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[8] = TMath::Cos(degrad*theta3);
// do the trick to eliminate most of the floating point errors
for (Int_t i=0; i<9; i++) {
if (TMath::Abs(fRotationMatrix[i])<1E-15) fRotationMatrix[i] = 0;
if (TMath::Abs(fRotationMatrix[i]-1)<1E-15) fRotationMatrix[i] = 1;
if (TMath::Abs(fRotationMatrix[i]+1)<1E-15) fRotationMatrix[i] = -1;
}
if (!IsValid()) Error("SetAngles", "invalid rotation (G3 angles, th1=%f phi1=%f, th2=%f ph2=%f, th3=%f phi3=%f)",
theta1,phi1,theta2,phi2,theta3,phi3);
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetAngles(Double_t &theta1, Double_t &phi1, Double_t &theta2, Double_t &phi2,
Double_t &theta3, Double_t &phi3) const
{
// Retreive rotation angles
Double_t raddeg = 180./TMath::Pi();
theta1 = raddeg*TMath::ACos(fRotationMatrix[6]);
theta2 = raddeg*TMath::ACos(fRotationMatrix[7]);
theta3 = raddeg*TMath::ACos(fRotationMatrix[8]);
if (TMath::Abs(fRotationMatrix[0])<1E-6 && TMath::Abs(fRotationMatrix[3])<1E-6) phi1=0.;
else phi1 = raddeg*TMath::ATan2(fRotationMatrix[3],fRotationMatrix[0]);
if (phi1<0) phi1+=360.;
if (TMath::Abs(fRotationMatrix[1])<1E-6 && TMath::Abs(fRotationMatrix[4])<1E-6) phi2=0.;
else phi2 = raddeg*TMath::ATan2(fRotationMatrix[4],fRotationMatrix[1]);
if (phi2<0) phi2+=360.;
if (TMath::Abs(fRotationMatrix[2])<1E-6 && TMath::Abs(fRotationMatrix[5])<1E-6) phi3=0.;
else phi3 = raddeg*TMath::ATan2(fRotationMatrix[5],fRotationMatrix[2]);
if (phi3<0) phi3+=360.;
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::Determinant() const
{
// computes determinant of the rotation matrix
Double_t
det = fRotationMatrix[0]*fRotationMatrix[4]*fRotationMatrix[8] +
fRotationMatrix[3]*fRotationMatrix[7]*fRotationMatrix[1] +
fRotationMatrix[6]*fRotationMatrix[1]*fRotationMatrix[5] -
fRotationMatrix[2]*fRotationMatrix[4]*fRotationMatrix[6] -
fRotationMatrix[5]*fRotationMatrix[7]*fRotationMatrix[0] -
fRotationMatrix[7]*fRotationMatrix[1]*fRotationMatrix[3];
return det;
}
//-----------------------------------------------------------------------------
void TGeoRotation::CheckMatrix()
{
// performes an orthogonality check and finds if the matrix is a reflection
// Warning("CheckMatrix", "orthogonality check not performed yet");
if (Determinant() < 0) {
SetBit(kGeoReflection);
// printf("matrix %s is reflection/n", GetName());
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetInverse(Double_t *invmat) const
{
// Get the inverse rotation matrix (which is simply the transpose)
if (!invmat) {
Error("GetInverse", "no place to store the inverse matrix");
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; i<3; i++) {
invmat[3*i+j] = fRotationMatrix[3*j+i];
}
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MultiplyBy(TGeoRotation *rot, Bool_t after)
{
const Double_t *matleft, *matright;
Double_t newmat[9] = {0};
if (after) {
matleft = &fRotationMatrix[0];
matright = rot->GetRotationMatrix();
} else {
matleft = rot->GetRotationMatrix();
matright = &fRotationMatrix[0];
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; j<3; j++) {
for (Int_t k=0; k<3; k++) {
newmat[3*i+j] += matleft[3*i+k] * matright[3*k+j];
}
}
}
memcpy(&fRotationMatrix[0], &newmat[0], kN9);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale()
{
// default constructor
SetBit(kGeoScale);
for (Int_t i=0; i<3; i++) fScale[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const TGeoScale &other)
:TGeoMatrix()
{
// Copy constructor
SetBit(kGeoScale);
const Double_t *scl = other.GetScale();
memcpy(fScale, scl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix("")
{
// default constructor
SetBit(kGeoScale);
SetDefaultName();
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const char *name, Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix(name)
{
// default constructor
SetBit(kGeoScale);
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::~TGeoScale()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoScale::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t scale[3];
scale[0] = 1./fScale[0];
scale[1] = 1./fScale[1];
scale[2] = 1./fScale[2];
h.SetScale(scale);
return h;
}
//-----------------------------------------------------------------------------
void TGeoScale::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// scale setter
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
Bool_t TGeoScale::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans()
{
// dummy ctor
SetBit(kGeoCombiTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoCombiTrans &other)
:TGeoMatrix()
{
// Copy ctor
SetBit(kGeoCombiTrans);
const Double_t *trans = other.GetTranslation();
const TGeoRotation rot = *other.GetRotation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoTranslation &tr, const TGeoRotation &rot)
{
SetBit(kGeoCombiTrans);
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = new TGeoRotation("");
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix("")
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name, Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::~TGeoCombiTrans()
{
// destructor
if (fRotation) delete fRotation;
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoCombiTrans::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
Double_t newrot[9];
const Double_t *rot = GetRotationMatrix();
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
newrot[0] = rot[0];
newrot[1] = rot[3];
newrot[2] = rot[6];
newrot[3] = rot[1];
newrot[4] = rot[4];
newrot[5] = rot[7];
newrot[6] = rot[2];
newrot[7] = rot[5];
newrot[8] = rot[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
// if (fRotation) fRotation->RegisterYourself();
}
if (!gGeoManager)
Warning("RegisterYourself", "cannot register without geometry");
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateX(Double_t angle)
{
// Combine this with a rotation about X axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateX", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateX(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = fTranslation[0];
tr[1] = c*fTranslation[1]+s*fTranslation[2];
tr[2] = -s*fTranslation[1]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateY(Double_t angle)
{
// Combine this with a rotation about Y axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateY", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateY(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]-s*fTranslation[2];
tr[1] = fTranslation[1];
tr[2] = s*fTranslation[0]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateZ(Double_t angle)
{
// Combine this with a rotation about Z axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateZ", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateZ(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]+s*fTranslation[1];
tr[1] = -s*fTranslation[0]+c*fTranslation[1];
tr[2] = fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(TGeoRotation *rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
const TGeoRotation r = *rot;
fRotation->SetRotation(r);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(const TGeoRotation &rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
fRotation->SetRotation(rot);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(const TGeoTranslation &tr)
{
// copy the translation component
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// set the translation component
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t *vect)
{
// set the translation component
fTranslation[0] = vect[0];
fTranslation[1] = vect[1];
fTranslation[2] = vect[2];
}
//-----------------------------------------------------------------------------
const Double_t *TGeoCombiTrans::GetRotationMatrix() const
{
// get the rotation array
if (!fRotation) return kIdentityMatrix;
return fRotation->GetRotationMatrix();
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans()
{
// dummy ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans("")
{
// ctor
SetBit(kGeoGenTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name, Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::~TGeoGenTrans()
{
// destructor
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::Clear(Option_t *)
{
// clear the fields of this transformation
memset(&fTranslation[0], 0, kN3);
memset(&fScale[0], 0, kN3);
if (fRotation) fRotation->Clear();
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// set the scale
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoGenTrans::Inverse() const
{
// Return a temporary inverse of this.
Error("Inverse", "not implemented");
static TGeoHMatrix h;
h = *this;
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoGenTrans::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity()
{
// dummy ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity(const char *name)
:TGeoMatrix(name)
{
// ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoIdentity::Inverse() const
{
// Return a temporary inverse of this.
return *gGeoIdentity;
}
/*************************************************************************
* TGeoHMatrix - Matrix class used for computing global transformations *
* Should NOT be used for node definition. An instance of this class *
* is generally used to pile-up local transformations starting from *
* the top level physical node, down to the current node. *
*************************************************************************/
ClassImp(TGeoHMatrix)
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix()
{
// dummy ctor
memset(&fTranslation[0], 0, kN3);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
memcpy(fScale,kUnitScale,kN3);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const char* name)
:TGeoMatrix(name)
{
// ctor
memset(&fTranslation[0], 0, kN3);
SetRotation(&kIdentityMatrix[0]);
SetScale(&kUnitScale[0]);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const TGeoMatrix &matrix)
{
// assignment
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
SetTranslation(matrix.GetTranslation());
} else {
memset(&fTranslation[0], 0, kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoHMatrix::~TGeoHMatrix()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix *matrix)
{
// assignment
if (matrix == this) return *this;
Clear();
if (matrix->IsIdentity()) return *this;
if (matrix->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix->GetTranslation(),kN3);
}
if (matrix->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix->GetRotationMatrix(),kN9);
}
if (matrix->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix->GetScale(),kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix &matrix)
{
// assignment
if (&matrix == this) return *this;
if (matrix.IsIdentity()) return *this;
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix.GetTranslation(),kN3);
} else {
memcpy(fTranslation,kNullVector,kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Clear(Option_t *)
{
// clear the data for this matrix
if (IsIdentity()) return;
if (IsTranslation()) {
ResetBit(kGeoTranslation);
memcpy(fTranslation,kNullVector,kN3);
}
if (IsRotation()) {
ResetBit(kGeoRotation);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (IsScale()) {
ResetBit(kGeoScale);
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoHMatrix::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
if (IsTranslation()) {
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
}
if (IsRotation()) {
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
}
if (IsScale()) {
Double_t sc[3];
sc[0] = 1./fScale[0];
sc[1] = 1./fScale[1];
sc[2] = 1./fScale[2];
h.SetScale(sc);
}
return h;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Multiply(const TGeoMatrix *right)
{
// multiply to the right with an other transformation
// if right is identity matrix, just return
if (right == gGeoIdentity) return;
const Double_t *r_tra = right->GetTranslation();
const Double_t *r_rot = right->GetRotationMatrix();
const Double_t *r_scl = right->GetScale();
if (IsIdentity()) {
if (right->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,r_rot,kN9);
}
if (right->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,r_scl,kN3);
}
if (right->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,r_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_rot[9];
if (right->IsRotation()) SetBit(kGeoRotation);
if (right->IsScale()) SetBit(kGeoScale);
if (right->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
fTranslation[i] += fRotationMatrix[3*i]*r_tra[0]
+ fRotationMatrix[3*i+1]*r_tra[1]
+ fRotationMatrix[3*i+2]*r_tra[2];
}
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = fRotationMatrix[3*i]*r_rot[j] +
fRotationMatrix[3*i+1]*r_rot[3+j] +
fRotationMatrix[3*i+2]*r_rot[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= r_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::MultiplyLeft(const TGeoMatrix *left)
{
// multiply to the left with an other transformation
// if right is identity matrix, just return
if (left == gGeoIdentity) return;
const Double_t *l_tra = left->GetTranslation();
const Double_t *l_rot = left->GetRotationMatrix();
const Double_t *l_scl = left->GetScale();
if (IsIdentity()) {
if (left->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,l_rot,kN9);
}
if (left->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,l_scl,kN3);
}
if (left->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,l_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_tra[3];
Double_t new_rot[9];
if (left->IsRotation()) SetBit(kGeoRotation);
if (left->IsScale()) SetBit(kGeoScale);
if (left->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
new_tra[i] = l_tra[i]
+ l_rot[3*i]* fTranslation[0]
+ l_rot[3*i+1]*fTranslation[1]
+ l_rot[3*i+2]*fTranslation[2];
}
memcpy(fTranslation,new_tra,kN3);
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = l_rot[3*i]*fRotationMatrix[j] +
l_rot[3*i+1]*fRotationMatrix[3+j] +
l_rot[3*i+2]*fRotationMatrix[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= l_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = fTranslation[0];
v[1] = c*fTranslation[1]+s*fTranslation[2];
v[2] = -s*fTranslation[1]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]-s*fTranslation[2];
v[1] = fTranslation[1];
v[2] = s*fTranslation[0]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]+s*fTranslation[1];
v[1] = -s*fTranslation[0]+c*fTranslation[1];
v[2] = fTranslation[2];
memcpy(fTranslation,v,kN3);
}
*/
//
//
// The base class TGeoMatrix defines abstract metods for:
//
// - translation, rotation and scale getters. Every derived class stores only
// its specific data, e.g. a translation stores an array of 3 doubles and a
// rotation an array of 9. However, asking which is the rotation array of a
// TGeoTranslation through the base TGeoMatrix interface is a legal operation.
// The answer in this case is a pointer to a global constant array representing
// an identity rotation.
// Double_t *TGeoMatrix::GetTranslation()
// Double_t *TGeoMatrix::GetRotation()
// Double_t *TGeoMatrix::GetScale()
//
// - MasterToLocal() and LocalToMaster() point and vector transformations :
// void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master)
// void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local)
// void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master)
// These allow correct conversion also for reflections.
// - Transformation type getters :
// Bool_t TGeoMatrix::IsIdentity()
// Bool_t TGeoMatrix::IsTranslation()
// Bool_t TGeoMatrix::IsRotation()
// Bool_t TGeoMatrix::IsScale()
// Bool_t TGeoMatrix::IsCombi() (translation + rotation)
// Bool_t TGeoMatrix::IsGeneral() (translation + rotation + scale)
//
// Combinations of basic transformations are represented by specific classes
// deriving from TGeoMatrix. In order to define a matrix as a combination of several
// others, a special class TGeoHMatrix is provided. Here is an example of matrix
// creation :
//
// Matrix creation example:
//
// root[0] TGeoRotation r1,r2;
// r1.SetAngles(90,0,30); // rotation defined by Euler angles
// r2.SetAngles(90,90,90,180,0,0); // rotation defined by GEANT3 angles
// TGeoTranslation t1(-10,10,0);
// TGeoTranslation t2(10,-10,5);
// TGeoCombiTrans c1(t1,r1);
// TGeoCombiTrans c2(t2,r2);
// TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix class
// root[7] TGeoHMatrix *ph = new TGeoHMatrix(hm); // this is the one we want to
// // use for positioning a volume
// root[8] ph->Print();
// ...
// pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by the manager
//
// Rule for matrix creation:
// - unless explicitly used for positioning nodes (TGeoVolume::AddNode()) all
// matrices deletion have to be managed by users. Matrices passed to geometry
// have to be created by using new() operator and their deletion is done by
// TGeoManager class.
//
// Available geometrical transformations
//
// 1. TGeoTranslation - represent a (dx,dy,dz) translation. Data members:
// Double_t fTranslation[3]. Translations can be added/subtracted.
// TGeoTranslation t1;
// t1->SetTranslation(-5,10,4);
// TGeoTranslation *t2 = new TGeoTranslation(4,3,10);
// t2->Subtract(&t1);
//
// 2. Rotations - represent a pure rotation. Data members: Double_t fRotationMatrix[3*3].
// Rotations can be defined either by Euler angles, either, by GEANT3 angles :
// TGeoRotation *r1 = new TGeoRotation();
// r1->SetAngles(phi, theta, psi); // all angles in degrees
// This represent the composition of : first a rotation about Z axis with
// angle phi, then a rotation with theta about the rotated X axis, and
// finally a rotation with psi about the new Z axis.
//
// r1->SetAngles(th1,phi1, th2,phi2, th3,phi3)
// This is a rotation defined in GEANT3 style. Theta and phi are the spherical
// angles of each axis of the rotated coordinate system with respect to the
// initial one. This construction allows definition of malformed rotations,
// e.g. not orthogonal. A check is performed and an error message is issued
// in this case.
//
// Specific utilities : determinant, inverse.
//
// 3. Scale transformations - represent a scale shrinking/enlargement. Data
// members :Double_t fScale[3]. Not fully implemented yet.
//
// 4. Combined transformations - represent a rotation folowed by a translation.
// Data members: Double_t fTranslation[3], TGeoRotation *fRotation.
// TGeoRotation *rot = new TGeoRotation("rot",10,20,30);
// TGeoTranslation trans;
// ...
// TGeoCombiTrans *c1 = new TGeoCombiTrans(trans, rot);
// TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot)
//
// 5. TGeoGenTrans - combined transformations including a scale. Not implemented.
// 6. TGeoIdentity - a generic singleton matrix representing a identity transformation
// NOTE: identified by the global variable gGeoIdentity.
//
//
#include "TObjArray.h"
#include "TGeoManager.h"
#include "TGeoMatrix.h"
TGeoIdentity *gGeoIdentity = 0;
const Int_t kN3 = 3*sizeof(Double_t);
const Int_t kN9 = 9*sizeof(Double_t);
// statics and globals
ClassImp(TGeoMatrix)
ClassImp(TGeoTranslation)
ClassImp(TGeoRotation)
ClassImp(TGeoScale)
ClassImp(TGeoCombiTrans)
ClassImp(TGeoGenTrans)
ClassImp(TGeoIdentity)
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix()
{
// dummy constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::TGeoMatrix(const char *name)
:TNamed(name, "")
{
// Constructor
}
//-----------------------------------------------------------------------------
TGeoMatrix::~TGeoMatrix()
{
// Destructor
if (IsRegistered() && gGeoManager) {
if (gGeoManager->GetListOfVolumes()) {
gGeoManager->GetListOfMatrices()->Remove(this);
Error("dtor", "a registered matrix was removed !!!");
}
}
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoMatrix::operator*(const TGeoMatrix &right) const
{
// Multiplication
static TGeoHMatrix h;
h = *this;
h.Multiply(&right);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoMatrix::IsRotAboutZ() const
{
// Returns true if no rotation or the rotation is about Z axis
if (IsIdentity()) return kTRUE;
const Double_t *rot = GetRotationMatrix();
if (TMath::Abs(rot[6])>1E-9) return kFALSE;
if (TMath::Abs(rot[7])>1E-9) return kFALSE;
if ((1.-TMath::Abs(rot[8]))>1E-9) return kFALSE;
return kTRUE;
}
//-----------------------------------------------------------------------------
Int_t TGeoMatrix::GetByteCount() const
{
// Get total size in bytes of this
Int_t count = 4+28+strlen(GetName())+strlen(GetTitle()); // fId + TNamed
if (IsTranslation()) count += 12;
if (IsScale()) count += 12;
if (IsCombi() || IsGeneral()) count += 4 + 36;
return count;
}
//-----------------------------------------------------------------------------
void TGeoMatrix::GetHomogenousMatrix(Double_t *hmat) const
{
// The homogenous matrix associated with the transformation is used for
// piling up's and visualization. A homogenous matrix is a 4*4 array
// containing the translation, the rotation and the scale components
//
// | R00*sx R01 R02 dx |
// | R10 R11*sy R12 dy |
// | R20 R21 R22*sz dz |
// | 0 0 0 1 |
//
// where Rij is the rotation matrix, (sx, sy, sz) is the scale
// transformation and (dx, dy, dz) is the translation.
Double_t *hmatrix = hmat;
const Double_t *mat = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
memcpy(hmatrix, mat, kN3);
mat += 3;
hmatrix += 3;
*hmatrix = 0.0;
hmatrix++;
}
memcpy(hmatrix, GetTranslation(), kN3);
hmatrix = hmat;
if (IsScale()) {
for (Int_t i=0; i<3; i++) {
*hmatrix *= GetScale()[i];
hmatrix += 5;
}
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = tr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
if (IsIdentity()) {
memcpy(master, local, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = bombtr[i]
+ local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
const Double_t *rot = GetRotationMatrix();
Double_t mt0 = master[0]-tr[0];
Double_t mt1 = master[1]-tr[1];
Double_t mt2 = master[2]-tr[2];
local[0] = mt0*rot[0] + mt1*rot[3] + mt2*rot[6];
local[1] = mt0*rot[1] + mt1*rot[4] + mt2*rot[7];
local[2] = mt0*rot[2] + mt1*rot[5] + mt2*rot[8];
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
if (IsIdentity()) {
memcpy(local, master, kN3);
return;
}
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = (master[0]-bombtr[0])*rot[i]
+ (master[1]-bombtr[1])*rot[i+3]
+ (master[2]-bombtr[2])*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::Print(Option_t *) const
{
// print the matrix in 4x4 format
const Double_t *rot = GetRotationMatrix();
const Double_t *tr = GetTranslation();
const Double_t *sc = GetScale();
printf("matrix %s - translation : %i rotation : %i scale : %in", GetName(),(Int_t)IsTranslation(),
(Int_t)IsRotation(), (Int_t)IsScale());
printf(" %g %g %g %gn", rot[0], rot[1], rot[2], (Double_t)0);
printf(" %g %g %g %gn", rot[3], rot[4], rot[5], (Double_t)0);
printf(" %g %g %g %gn", rot[6], rot[7], rot[8], (Double_t)0);
printf(" %g %g %g %gn", tr[0], tr[1], tr[2], (Double_t)1);
if (IsScale()) printf("Scale : %g %g %gn", sc[0], sc[1], sc[2]);
}
//-----------------------------------------------------------------------------
void TGeoMatrix::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
}
}
//-----------------------------------------------------------------------------
void TGeoMatrix::SetDefaultName()
{
// If no name was supplied in the ctor, the type of transformation is checked.
// A letter will be prepended to the name :
// t - translation
// r - rotation
// s - scale
// c - combi (translation + rotation)
// g - general (tr+rot+scale)
// The index of the transformation in gGeoManager list of transformations will
// be appended.
if (!gGeoManager) return;
if (strlen(GetName())) return;
char type = 'n';
if (IsTranslation()) type = 't';
if (IsRotation()) type = 'r';
if (IsScale()) type = 's';
if (IsCombi()) type = 'c';
if (IsGeneral()) type = 'g';
TObjArray *matrices = gGeoManager->GetListOfMatrices();
Int_t index = 0;
if (matrices) index =matrices->GetEntriesFast() - 1;
Int_t digits = 1;
Int_t num = 10;
while ((Int_t)(index/num)) {
digits++;
num *= 10;
}
char *name = new char[digits+2];
sprintf(name, "%c%i", type, index);
SetName(name);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation()
{
// Default constructor
SetBit(kGeoTranslation);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const TGeoTranslation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoTranslation);
const Double_t *transl = other.GetTranslation();
memcpy(fTranslation, transl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix("")
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetDefaultName();
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoTranslation::TGeoTranslation(const char *name, Double_t dx, Double_t dy, Double_t dz)
:TGeoMatrix(name)
{
// Default constructor defining the translation
SetBit(kGeoTranslation);
SetTranslation(dx, dy, dz);
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoTranslation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
return h;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Add(const TGeoTranslation *other)
{
// Adding a translation to this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] += trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::Subtract(const TGeoTranslation *other)
{
// Subtracting a translation from this one
const Double_t *trans = other->GetTranslation();
for (Int_t i=0; i<3; i++)
fTranslation[i] -= trans[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// Set translation components
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
master[i] = tr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterVect(const Double_t *local, Double_t *master) const
{
// convert a vector to MARS
memcpy(master, local, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::LocalToMasterBomb(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->BombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
master[i] = bombtr[i] + local[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
for (Int_t i=0; i<3; i++)
local[i] = master[i]-tr[i];
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalVect(const Double_t *master, Double_t *local) const
{
// convert a vector from MARS to local
memcpy(local, master, kN3);
}
//-----------------------------------------------------------------------------
void TGeoTranslation::MasterToLocalBomb(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *tr = GetTranslation();
Double_t bombtr[3];
gGeoManager->UnbombTranslation(tr, &bombtr[0]);
for (Int_t i=0; i<3; i++)
local[i] = master[i]-bombtr[i];
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation()
{
// Default constructor.
SetBit(kGeoRotation);
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const TGeoRotation &other)
:TGeoMatrix()
{
// Copy ctor.
SetBit(kGeoRotation);
SetRotation(other);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name)
:TGeoMatrix(name)
{
// Named rotation constructor
for (Int_t i=0; i<9; i++) {
if (i%4) fRotationMatrix[i] = 0;
else fRotationMatrix[i] = 1.0;
}
SetBit(kGeoRotation);
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t phi, Double_t theta, Double_t psi)
:TGeoMatrix(name)
{
// Default rotation constructor with Euler angles. Phi is the rotation angle about
// Z axis and is done first, theta is the rotation about new Y and is done
// second, psi is the rotation angle about new Z and is done third. All angles are in
// degrees.
SetBit(kGeoRotation);
SetAngles(phi, theta, psi);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoRotation::TGeoRotation(const char *name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
:TGeoMatrix(name)
{
// Rotation constructor a la GEANT3. Angles theta(i), phi(i) are the polar and azimuthal
// angles of the (i) axis of the rotated system with respect to the initial non-rotated
// system.
// Example : the identity matrix (no rotation) is composed by
// theta1=90, phi1=0, theta2=90, phi2=90, theta3=0, phi3=0
SetBit(kGeoRotation);
SetAngles(theta1, phi1, theta2, phi2, theta3, phi3);
CheckMatrix();
SetDefaultName();
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoRotation::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoRotation::IsValid() const
{
// Perform orthogonality test for rotation.
const Double_t *r = fRotationMatrix;
Double_t cij;
for (Int_t i=0; i<2; i++) {
for (Int_t j=i+1; j<3; j++) {
// check columns
cij = TMath::Abs(r[i]*r[j]+r[i+3]*r[j+3]+r[i+6]*r[j+6]);
if (cij>1E-4) return kFALSE;
// check rows
cij = TMath::Abs(r[3*i]*r[3*j]+r[3*i+1]*r[3*j+1]+r[3*i+2]*r[3*j+2]);
if (cij>1E-4) return kFALSE;
}
}
return kTRUE;
}
//-----------------------------------------------------------------------------
void TGeoRotation::Clear(Option_t *)
{
// reset data members to 0
memset(&fRotationMatrix[0], 0, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::FastRotZ(Double_t *sincos)
{
fRotationMatrix[0] = sincos[1];
fRotationMatrix[1] = -sincos[0];
fRotationMatrix[3] = sincos[0];
fRotationMatrix[4] = sincos[1];
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::GetPhiRotation() const
{
//--- Returns rotation angle about Z axis in degrees.
Double_t phi = 180.*TMath::ATan2(fRotationMatrix[1], fRotationMatrix[0])/TMath::Pi();
return phi;
}
//-----------------------------------------------------------------------------
void TGeoRotation::LocalToMaster(const Double_t *local, Double_t *master) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
master[i] = local[0]*rot[3*i]
+ local[1]*rot[3*i+1]
+ local[2]*rot[3*i+2];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MasterToLocal(const Double_t *master, Double_t *local) const
{
// convert a point by multiplying its column vector (x, y, z, 1) to matrix
const Double_t *rot = GetRotationMatrix();
for (Int_t i=0; i<3; i++) {
local[i] = master[0]*rot[i]
+ master[1]*rot[i+3]
+ master[2]*rot[i+6];
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetRotation(const TGeoRotation &other)
{
// Copy rotation elements from other rotation matrix.
const Double_t *rot = other.GetRotationMatrix();
memcpy(fRotationMatrix, rot, kN9);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t phi, Double_t theta, Double_t psi)
{
// Set matrix elements according to Euler angles
Double_t degrad = TMath::Pi()/180.;
Double_t sinphi = TMath::Sin(degrad*phi);
Double_t cosphi = TMath::Cos(degrad*phi);
Double_t sinthe = TMath::Sin(degrad*theta);
Double_t costhe = TMath::Cos(degrad*theta);
Double_t sinpsi = TMath::Sin(degrad*psi);
Double_t cospsi = TMath::Cos(degrad*psi);
fRotationMatrix[0] = cospsi*cosphi - costhe*sinphi*sinpsi;
fRotationMatrix[1] = -sinpsi*cosphi - costhe*sinphi*cospsi;
fRotationMatrix[2] = sinthe*sinphi;
fRotationMatrix[3] = cospsi*sinphi + costhe*cosphi*sinpsi;
fRotationMatrix[4] = -sinpsi*sinphi + costhe*cosphi*cospsi;
fRotationMatrix[5] = -sinthe*cosphi;
fRotationMatrix[6] = sinpsi*sinthe;
fRotationMatrix[7] = cospsi*sinthe;
fRotationMatrix[8] = costhe;
if (!IsValid()) Error("SetAngles", "invalid rotation (Euler angles : phi=%f theta=%f psi=%f)",phi,theta,psi);
}
//-----------------------------------------------------------------------------
void TGeoRotation::SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2,
Double_t theta3, Double_t phi3)
{
// Set matrix elements in the GEANT3 way
Double_t degrad = TMath::Pi()/180.;
fRotationMatrix[0] = TMath::Cos(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[3] = TMath::Sin(degrad*phi1)*TMath::Sin(degrad*theta1);
fRotationMatrix[6] = TMath::Cos(degrad*theta1);
fRotationMatrix[1] = TMath::Cos(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[4] = TMath::Sin(degrad*phi2)*TMath::Sin(degrad*theta2);
fRotationMatrix[7] = TMath::Cos(degrad*theta2);
fRotationMatrix[2] = TMath::Cos(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[5] = TMath::Sin(degrad*phi3)*TMath::Sin(degrad*theta3);
fRotationMatrix[8] = TMath::Cos(degrad*theta3);
// do the trick to eliminate most of the floating point errors
for (Int_t i=0; i<9; i++) {
if (TMath::Abs(fRotationMatrix[i])<1E-15) fRotationMatrix[i] = 0;
if (TMath::Abs(fRotationMatrix[i]-1)<1E-15) fRotationMatrix[i] = 1;
if (TMath::Abs(fRotationMatrix[i]+1)<1E-15) fRotationMatrix[i] = -1;
}
if (!IsValid()) Error("SetAngles", "invalid rotation (G3 angles, th1=%f phi1=%f, th2=%f ph2=%f, th3=%f phi3=%f)",
theta1,phi1,theta2,phi2,theta3,phi3);
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetAngles(Double_t &theta1, Double_t &phi1, Double_t &theta2, Double_t &phi2,
Double_t &theta3, Double_t &phi3) const
{
// Retreive rotation angles
Double_t raddeg = 180./TMath::Pi();
theta1 = raddeg*TMath::ACos(fRotationMatrix[6]);
theta2 = raddeg*TMath::ACos(fRotationMatrix[7]);
theta3 = raddeg*TMath::ACos(fRotationMatrix[8]);
if (TMath::Abs(fRotationMatrix[0])<1E-6 && TMath::Abs(fRotationMatrix[3])<1E-6) phi1=0.;
else phi1 = raddeg*TMath::ATan2(fRotationMatrix[3],fRotationMatrix[0]);
if (phi1<0) phi1+=360.;
if (TMath::Abs(fRotationMatrix[1])<1E-6 && TMath::Abs(fRotationMatrix[4])<1E-6) phi2=0.;
else phi2 = raddeg*TMath::ATan2(fRotationMatrix[4],fRotationMatrix[1]);
if (phi2<0) phi2+=360.;
if (TMath::Abs(fRotationMatrix[2])<1E-6 && TMath::Abs(fRotationMatrix[5])<1E-6) phi3=0.;
else phi3 = raddeg*TMath::ATan2(fRotationMatrix[5],fRotationMatrix[2]);
if (phi3<0) phi3+=360.;
}
//-----------------------------------------------------------------------------
Double_t TGeoRotation::Determinant() const
{
// computes determinant of the rotation matrix
Double_t
det = fRotationMatrix[0]*fRotationMatrix[4]*fRotationMatrix[8] +
fRotationMatrix[3]*fRotationMatrix[7]*fRotationMatrix[1] +
fRotationMatrix[6]*fRotationMatrix[1]*fRotationMatrix[5] -
fRotationMatrix[2]*fRotationMatrix[4]*fRotationMatrix[6] -
fRotationMatrix[5]*fRotationMatrix[7]*fRotationMatrix[0] -
fRotationMatrix[7]*fRotationMatrix[1]*fRotationMatrix[3];
return det;
}
//-----------------------------------------------------------------------------
void TGeoRotation::CheckMatrix()
{
// performes an orthogonality check and finds if the matrix is a reflection
// Warning("CheckMatrix", "orthogonality check not performed yet");
if (Determinant() < 0) {
SetBit(kGeoReflection);
// printf("matrix %s is reflection/n", GetName());
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::GetInverse(Double_t *invmat) const
{
// Get the inverse rotation matrix (which is simply the transpose)
if (!invmat) {
Error("GetInverse", "no place to store the inverse matrix");
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; i<3; i++) {
invmat[3*i+j] = fRotationMatrix[3*j+i];
}
}
}
//-----------------------------------------------------------------------------
void TGeoRotation::MultiplyBy(TGeoRotation *rot, Bool_t after)
{
const Double_t *matleft, *matright;
Double_t newmat[9] = {0};
if (after) {
matleft = &fRotationMatrix[0];
matright = rot->GetRotationMatrix();
} else {
matleft = rot->GetRotationMatrix();
matright = &fRotationMatrix[0];
}
for (Int_t i=0; i<3; i++) {
for (Int_t j=0; j<3; j++) {
for (Int_t k=0; k<3; k++) {
newmat[3*i+j] += matleft[3*i+k] * matright[3*k+j];
}
}
}
memcpy(&fRotationMatrix[0], &newmat[0], kN9);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale()
{
// default constructor
SetBit(kGeoScale);
for (Int_t i=0; i<3; i++) fScale[i] = 0;
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const TGeoScale &other)
:TGeoMatrix()
{
// Copy constructor
SetBit(kGeoScale);
const Double_t *scl = other.GetScale();
memcpy(fScale, scl, kN3);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix("")
{
// default constructor
SetBit(kGeoScale);
SetDefaultName();
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::TGeoScale(const char *name, Double_t sx, Double_t sy, Double_t sz)
:TGeoMatrix(name)
{
// default constructor
SetBit(kGeoScale);
SetScale(sx, sy, sz);
}
//-----------------------------------------------------------------------------
TGeoScale::~TGeoScale()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoScale::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t scale[3];
scale[0] = 1./fScale[0];
scale[1] = 1./fScale[1];
scale[2] = 1./fScale[2];
h.SetScale(scale);
return h;
}
//-----------------------------------------------------------------------------
void TGeoScale::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// scale setter
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
Bool_t TGeoScale::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans()
{
// dummy ctor
SetBit(kGeoCombiTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoCombiTrans &other)
:TGeoMatrix()
{
// Copy ctor
SetBit(kGeoCombiTrans);
const Double_t *trans = other.GetTranslation();
const TGeoRotation rot = *other.GetRotation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
SetName(other.GetName());
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const TGeoTranslation &tr, const TGeoRotation &rot)
{
SetBit(kGeoCombiTrans);
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
fRotation = new TGeoRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
fRotation = new TGeoRotation("");
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix("")
{
// ctor
SetBit(kGeoCombiTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::TGeoCombiTrans(const char *name, Double_t dx, Double_t dy, Double_t dz, TGeoRotation *rot)
:TGeoMatrix(name)
{
// ctor
SetBit(kGeoCombiTrans);
SetTranslation(dx, dy, dz);
fRotation = 0;
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoCombiTrans::~TGeoCombiTrans()
{
// destructor
if (fRotation) delete fRotation;
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoCombiTrans::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
Double_t tr[3];
Double_t newrot[9];
const Double_t *rot = GetRotationMatrix();
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
newrot[0] = rot[0];
newrot[1] = rot[3];
newrot[2] = rot[6];
newrot[3] = rot[1];
newrot[4] = rot[4];
newrot[5] = rot[7];
newrot[6] = rot[2];
newrot[7] = rot[5];
newrot[8] = rot[8];
h.SetRotation(newrot);
return h;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RegisterYourself()
{
if (!IsRegistered() && gGeoManager) {
gGeoManager->RegisterMatrix(this);
SetBit(kGeoRegistered);
// if (fRotation) fRotation->RegisterYourself();
}
if (!gGeoManager)
Warning("RegisterYourself", "cannot register without geometry");
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateX(Double_t angle)
{
// Combine this with a rotation about X axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateX", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateX(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = fTranslation[0];
tr[1] = c*fTranslation[1]+s*fTranslation[2];
tr[2] = -s*fTranslation[1]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateY(Double_t angle)
{
// Combine this with a rotation about Y axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateY", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateY(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]-s*fTranslation[2];
tr[1] = fTranslation[1];
tr[2] = s*fTranslation[0]+c*fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::RotateZ(Double_t angle)
{
// Combine this with a rotation about Z axis. Current rotation must be not NULL.
if (!fRotation) {
Warning("RotateZ", "cannot rotate since original rotation is not defined");
return;
}
fRotation->RotateZ(angle);
if (fTranslation[0]==0 && fTranslation[1]==0 && fTranslation[2]==0) return;
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t tr[3];
tr[0] = c*fTranslation[0]+s*fTranslation[1];
tr[1] = -s*fTranslation[0]+c*fTranslation[1];
tr[2] = fTranslation[2];
SetTranslation(tr);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(TGeoRotation *rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
const TGeoRotation r = *rot;
fRotation->SetRotation(r);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetRotation(const TGeoRotation &rot)
{
// Copy the rotation from another one.
if (!fRotation) fRotation = new TGeoRotation();
fRotation->SetRotation(rot);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(const TGeoTranslation &tr)
{
// copy the translation component
const Double_t *trans = tr.GetTranslation();
memcpy(fTranslation, trans, kN3);
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t dx, Double_t dy, Double_t dz)
{
// set the translation component
fTranslation[0] = dx;
fTranslation[1] = dy;
fTranslation[2] = dz;
}
//-----------------------------------------------------------------------------
void TGeoCombiTrans::SetTranslation(Double_t *vect)
{
// set the translation component
fTranslation[0] = vect[0];
fTranslation[1] = vect[1];
fTranslation[2] = vect[2];
}
//-----------------------------------------------------------------------------
const Double_t *TGeoCombiTrans::GetRotationMatrix() const
{
// get the rotation array
if (!fRotation) return kIdentityMatrix;
return fRotation->GetRotationMatrix();
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans()
{
// dummy ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
for (Int_t i=0; i<3; i++) fTranslation[i] = 0.0;
for (Int_t j=0; j<3; j++) fScale[j] = 1.0;
fRotation = 0;
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans("")
{
// ctor
SetBit(kGeoGenTrans);
SetDefaultName();
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::TGeoGenTrans(const char *name, Double_t dx, Double_t dy, Double_t dz,
Double_t sx, Double_t sy, Double_t sz, TGeoRotation *rot)
:TGeoCombiTrans(name)
{
// ctor
SetBit(kGeoGenTrans);
SetTranslation(dx, dy, dz);
SetScale(sx, sy, sz);
SetRotation(rot);
}
//-----------------------------------------------------------------------------
TGeoGenTrans::~TGeoGenTrans()
{
// destructor
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::Clear(Option_t *)
{
// clear the fields of this transformation
memset(&fTranslation[0], 0, kN3);
memset(&fScale[0], 0, kN3);
if (fRotation) fRotation->Clear();
}
//-----------------------------------------------------------------------------
void TGeoGenTrans::SetScale(Double_t sx, Double_t sy, Double_t sz)
{
// set the scale
fScale[0] = sx;
fScale[1] = sy;
fScale[2] = sz;
if (!(Normalize())) {
Error("ctor", "Invalid scale");
return;
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoGenTrans::Inverse() const
{
// Return a temporary inverse of this.
Error("Inverse", "not implemented");
static TGeoHMatrix h;
h = *this;
return h;
}
//-----------------------------------------------------------------------------
Bool_t TGeoGenTrans::Normalize()
{
// A scale transformation should be normalized by sx*sy*sz factor
Double_t normfactor = fScale[0]*fScale[1]*fScale[2];
if (normfactor <= 1E-5) return kFALSE;
for (Int_t i=0; i<3; i++)
fScale[i] /= normfactor;
return kTRUE;
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity()
{
// dummy ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoIdentity::TGeoIdentity(const char *name)
:TGeoMatrix(name)
{
// ctor
if (!gGeoIdentity) gGeoIdentity = this;
RegisterYourself();
}
//-----------------------------------------------------------------------------
TGeoMatrix &TGeoIdentity::Inverse() const
{
// Return a temporary inverse of this.
return *gGeoIdentity;
}
/*************************************************************************
* TGeoHMatrix - Matrix class used for computing global transformations *
* Should NOT be used for node definition. An instance of this class *
* is generally used to pile-up local transformations starting from *
* the top level physical node, down to the current node. *
*************************************************************************/
ClassImp(TGeoHMatrix)
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix()
{
// dummy ctor
memset(&fTranslation[0], 0, kN3);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
memcpy(fScale,kUnitScale,kN3);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const char* name)
:TGeoMatrix(name)
{
// ctor
memset(&fTranslation[0], 0, kN3);
SetRotation(&kIdentityMatrix[0]);
SetScale(&kUnitScale[0]);
}
//-----------------------------------------------------------------------------
TGeoHMatrix::TGeoHMatrix(const TGeoMatrix &matrix)
{
// assignment
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
SetTranslation(matrix.GetTranslation());
} else {
memset(&fTranslation[0], 0, kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoHMatrix::~TGeoHMatrix()
{
// destructor
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix *matrix)
{
// assignment
if (matrix == this) return *this;
Clear();
if (matrix->IsIdentity()) return *this;
if (matrix->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix->GetTranslation(),kN3);
}
if (matrix->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix->GetRotationMatrix(),kN9);
}
if (matrix->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix->GetScale(),kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
TGeoHMatrix &TGeoHMatrix::operator=(const TGeoMatrix &matrix)
{
// assignment
if (&matrix == this) return *this;
if (matrix.IsIdentity()) return *this;
if (matrix.IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,matrix.GetTranslation(),kN3);
} else {
memcpy(fTranslation,kNullVector,kN3);
}
if (matrix.IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,matrix.GetRotationMatrix(),kN9);
} else {
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (matrix.IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,matrix.GetScale(),kN3);
} else {
memcpy(fScale,kUnitScale,kN3);
}
return *this;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Clear(Option_t *)
{
// clear the data for this matrix
if (IsIdentity()) return;
if (IsTranslation()) {
ResetBit(kGeoTranslation);
memcpy(fTranslation,kNullVector,kN3);
}
if (IsRotation()) {
ResetBit(kGeoRotation);
memcpy(fRotationMatrix,kIdentityMatrix,kN9);
}
if (IsScale()) {
ResetBit(kGeoScale);
memcpy(fScale,kUnitScale,kN3);
}
}
//-----------------------------------------------------------------------------
TGeoMatrix& TGeoHMatrix::Inverse() const
{
// Return a temporary inverse of this.
static TGeoHMatrix h;
h = *this;
if (IsTranslation()) {
Double_t tr[3];
tr[0] = -fTranslation[0];
tr[1] = -fTranslation[1];
tr[2] = -fTranslation[2];
h.SetTranslation(tr);
}
if (IsRotation()) {
Double_t newrot[9];
newrot[0] = fRotationMatrix[0];
newrot[1] = fRotationMatrix[3];
newrot[2] = fRotationMatrix[6];
newrot[3] = fRotationMatrix[1];
newrot[4] = fRotationMatrix[4];
newrot[5] = fRotationMatrix[7];
newrot[6] = fRotationMatrix[2];
newrot[7] = fRotationMatrix[5];
newrot[8] = fRotationMatrix[8];
h.SetRotation(newrot);
}
if (IsScale()) {
Double_t sc[3];
sc[0] = 1./fScale[0];
sc[1] = 1./fScale[1];
sc[2] = 1./fScale[2];
h.SetScale(sc);
}
return h;
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::Multiply(const TGeoMatrix *right)
{
// multiply to the right with an other transformation
// if right is identity matrix, just return
if (right == gGeoIdentity) return;
const Double_t *r_tra = right->GetTranslation();
const Double_t *r_rot = right->GetRotationMatrix();
const Double_t *r_scl = right->GetScale();
if (IsIdentity()) {
if (right->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,r_rot,kN9);
}
if (right->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,r_scl,kN3);
}
if (right->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,r_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_rot[9];
if (right->IsRotation()) SetBit(kGeoRotation);
if (right->IsScale()) SetBit(kGeoScale);
if (right->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
fTranslation[i] += fRotationMatrix[3*i]*r_tra[0]
+ fRotationMatrix[3*i+1]*r_tra[1]
+ fRotationMatrix[3*i+2]*r_tra[2];
}
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = fRotationMatrix[3*i]*r_rot[j] +
fRotationMatrix[3*i+1]*r_rot[3+j] +
fRotationMatrix[3*i+2]*r_rot[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= r_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::MultiplyLeft(const TGeoMatrix *left)
{
// multiply to the left with an other transformation
// if right is identity matrix, just return
if (left == gGeoIdentity) return;
const Double_t *l_tra = left->GetTranslation();
const Double_t *l_rot = left->GetRotationMatrix();
const Double_t *l_scl = left->GetScale();
if (IsIdentity()) {
if (left->IsRotation()) {
SetBit(kGeoRotation);
memcpy(fRotationMatrix,l_rot,kN9);
}
if (left->IsScale()) {
SetBit(kGeoScale);
memcpy(fScale,l_scl,kN3);
}
if (left->IsTranslation()) {
SetBit(kGeoTranslation);
memcpy(fTranslation,l_tra,kN3);
}
return;
}
Int_t i, j;
Double_t new_tra[3];
Double_t new_rot[9];
if (left->IsRotation()) SetBit(kGeoRotation);
if (left->IsScale()) SetBit(kGeoScale);
if (left->IsTranslation()) SetBit(kGeoTranslation);
// new translation
if (IsTranslation()) {
for (i=0; i<3; i++) {
new_tra[i] = l_tra[i]
+ l_rot[3*i]* fTranslation[0]
+ l_rot[3*i+1]*fTranslation[1]
+ l_rot[3*i+2]*fTranslation[2];
}
memcpy(fTranslation,new_tra,kN3);
}
if (IsRotation()) {
// new rotation
for (i=0; i<3; i++) {
for (j=0; j<3; j++) {
new_rot[3*i+j] = l_rot[3*i]*fRotationMatrix[j] +
l_rot[3*i+1]*fRotationMatrix[3+j] +
l_rot[3*i+2]*fRotationMatrix[6+j];
}
}
memcpy(fRotationMatrix,new_rot,kN9);
}
// new scale
if (IsScale()) {
for (i=0; i<3; i++) fScale[i] *= l_scl[i];
}
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateX(Double_t angle)
{
// Rotate about X axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = fRotationMatrix[j];
v[1] = c*fRotationMatrix[j+1]+s*fRotationMatrix[j+2];
v[2] = -s*fRotationMatrix[j+1]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = fTranslation[0];
v[1] = c*fTranslation[1]+s*fTranslation[2];
v[2] = -s*fTranslation[1]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateY(Double_t angle)
{
// Rotate about Y axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]-s*fRotationMatrix[j+2];
v[1] = fRotationMatrix[j+1];
v[2] = s*fRotationMatrix[j]+c*fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]-s*fTranslation[2];
v[1] = fTranslation[1];
v[2] = s*fTranslation[0]+c*fTranslation[2];
memcpy(fTranslation,v,kN3);
}
//-----------------------------------------------------------------------------
void TGeoHMatrix::RotateZ(Double_t angle)
{
// Rotate about Z axis with angle expressed in degrees.
Double_t phi = angle*TMath::DegToRad();
Double_t c = TMath::Cos(phi);
Double_t s = TMath::Sin(phi);
Double_t v[3];
Int_t j;
for (Int_t i=0; i<3; i++) {
j = 3*i;
v[0] = c*fRotationMatrix[j]+s*fRotationMatrix[j+1];
v[1] = -s*fRotationMatrix[j]+c*fRotationMatrix[j+1];
v[2] = fRotationMatrix[j+2];
memcpy(&fRotationMatrix[j], v, kN3);
}
SetBit(kGeoRotation);
v[0] = c*fTranslation[0]+s*fTranslation[1];
v[1] = -s*fTranslation[0]+c*fTranslation[1];
v[2] = fTranslation[2];
memcpy(fTranslation,v,kN3);
}