library: libHist
#include "TH1.h" |
TH1
class description - source file - inheritance tree (.pdf)
private:
Int_t AxisChoice(Option_t* axis) const
void Build()
Int_t FitOptionsMake(Option_t* option, Foption_t& Foption)
protected:
TH1()
TH1(const char* name, const char* title, Int_t nbinsx, Axis_t xlow, Axis_t xup)
TH1(const char* name, const char* title, Int_t nbinsx, const Float_t* xbins)
TH1(const char* name, const char* title, Int_t nbinsx, const Double_t* xbins)
virtual Int_t BufferFill(Axis_t x, Stat_t w)
virtual void Copy(TObject& hnew) const
virtual void SavePrimitiveHelp(ofstream& out, Option_t* option)
public:
TH1(const TH1&)
virtual ~TH1()
virtual void Add(TF1* h1, Double_t c1 = 1, Option_t* option)
virtual void Add(const TH1* h1, Double_t c1 = 1)
virtual void Add(const TH1* h, const TH1* h2, Double_t c1 = 1, Double_t c2 = 1)
virtual void AddBinContent(Int_t bin)
virtual void AddBinContent(Int_t bin, Stat_t w)
static void AddDirectory(Bool_t add = kTRUE)
static Bool_t AddDirectoryStatus()
virtual void Browse(TBrowser* b)
virtual Int_t BufferEmpty(Int_t action = 0)
virtual Double_t Chi2Test(TH1* h, Option_t* option, Int_t constraint = 0)
static TClass* Class()
virtual Double_t ComputeIntegral()
virtual Int_t DistancetoPrimitive(Int_t px, Int_t py)
virtual void Divide(TF1* f1, Double_t c1 = 1)
virtual void Divide(const TH1* h1)
virtual void Divide(const TH1* h1, const TH1* h2, Double_t c1 = 1, Double_t c2 = 1, Option_t* option)
virtual void Draw(Option_t* option)
virtual TH1* DrawCopy(Option_t* option) const
virtual TH1* DrawNormalized(Option_t* option, Double_t norm = 1) const
virtual void DrawPanel()
virtual void Eval(TF1* f1, Option_t* option)
virtual void ExecuteEvent(Int_t event, Int_t px, Int_t py)
virtual Int_t Fill(Axis_t x)
virtual Int_t Fill(Axis_t x, Stat_t w)
virtual Int_t Fill(const char* name, Stat_t w)
virtual void FillN(Int_t ntimes, const Axis_t* x, const Double_t* w, Int_t stride = 1)
virtual void FillN(Int_t, const Axis_t*, const Axis_t*, const Double_t*, Int_t)
virtual void FillRandom(const char* fname, Int_t ntimes = 5000)
virtual void FillRandom(TH1* h, Int_t ntimes = 5000)
virtual Int_t FindBin(Axis_t x, Axis_t y = 0, Axis_t z = 0)
virtual TObject* FindObject(const char* name) const
virtual TObject* FindObject(const TObject* obj) const
virtual Int_t Fit(const char* formula, Option_t* option, Option_t* goption, Axis_t xmin = 0, Axis_t xmax = 0)
virtual Int_t Fit(TF1* f1, Option_t* option, Option_t* goption, Axis_t xmin = 0, Axis_t xmax = 0)
virtual void FitPanel()
TH1* GetAsymmetry(TH1* h2, Double_t c2 = 1, Double_t dc2 = 0)
virtual Color_t GetAxisColor(Option_t* axis = "X") const
virtual Float_t GetBarOffset() const
virtual Float_t GetBarWidth() const
virtual Int_t GetBin(Int_t binx, Int_t biny = 0, Int_t binz = 0) const
virtual Axis_t GetBinCenter(Int_t bin) const
virtual Stat_t GetBinContent(Int_t bin) const
virtual Stat_t GetBinContent(Int_t binx, Int_t biny) const
virtual Stat_t GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
virtual Stat_t GetBinError(Int_t bin) const
virtual Stat_t GetBinError(Int_t binx, Int_t biny) const
virtual Stat_t GetBinError(Int_t binx, Int_t biny, Int_t binz) const
virtual Axis_t GetBinLowEdge(Int_t bin) const
virtual Axis_t GetBinWidth(Int_t bin) const
const Double_t* GetBuffer() const
Int_t GetBufferLength() const
Int_t GetBufferSize() const
virtual Stat_t GetCellContent(Int_t binx, Int_t biny) const
virtual Stat_t GetCellError(Int_t binx, Int_t biny) const
virtual void GetCenter(Axis_t* center) const
virtual Int_t GetContour(Double_t* levels = 0)
virtual Double_t GetContourLevel(Int_t level) const
virtual Double_t GetContourLevelPad(Int_t level) const
static Int_t GetDefaultBufferSize()
virtual Int_t GetDimension() const
TDirectory* GetDirectory() const
virtual Stat_t GetEntries() const
virtual TF1* GetFunction(const char* name) const
virtual Double_t* GetIntegral()
virtual Color_t GetLabelColor(Option_t* axis = "X") const
virtual Style_t GetLabelFont(Option_t* axis = "X") const
virtual Float_t GetLabelOffset(Option_t* axis = "X") const
virtual Float_t GetLabelSize(Option_t* axis = "X") const
TList* GetListOfFunctions() const
virtual void GetLowEdge(Axis_t* edge) const
virtual Double_t GetMaximum(Double_t maxval = FLT_MAX) const
virtual Int_t GetMaximumBin() const
virtual Int_t GetMaximumBin(Int_t& locmax, Int_t& locmay, Int_t& locmaz) const
virtual Double_t GetMaximumStored() const
virtual Double_t GetMean(Int_t axis = 1) const
virtual Double_t GetMeanError(Int_t axis = 1) const
virtual Double_t GetMinimum(Double_t minval = -FLT_MAX) const
virtual Int_t GetMinimumBin() const
virtual Int_t GetMinimumBin(Int_t& locmix, Int_t& locmiy, Int_t& locmiz) const
virtual Double_t GetMinimumStored() const
virtual Int_t GetNbinsX() const
virtual Int_t GetNbinsY() const
virtual Int_t GetNbinsZ() const
virtual Int_t GetNdivisions(Option_t* axis = "X") const
virtual Double_t GetNormFactor() const
virtual char* GetObjectInfo(Int_t px, Int_t py) const
virtual Option_t* GetOption() const
TVirtualHistPainter* GetPainter()
virtual Int_t GetQuantiles(Int_t nprobSum, Double_t* q, const Double_t* probSum = 0)
virtual Axis_t GetRandom() const
virtual Double_t GetRMS(Int_t axis = 1) const
virtual Double_t GetRMSError(Int_t axis = 1) const
virtual void GetStats(Stat_t* stats) const
virtual Stat_t GetSumOfWeights() const
virtual Int_t GetSumw2N() const
virtual Float_t GetTickLength(Option_t* axis = "X") const
virtual Float_t GetTitleOffset(Option_t* axis = "X") const
virtual Float_t GetTitleSize(Option_t* axis = "X") const
TAxis* GetXaxis() const
TAxis* GetYaxis() const
TAxis* GetZaxis() const
virtual Stat_t Integral(Option_t* option) const
virtual Stat_t Integral(Int_t binx1, Int_t binx2, Option_t* option) const
virtual Stat_t Integral(Int_t, Int_t, Int_t, Int_t, Option_t*) const
virtual Stat_t Integral(Int_t, Int_t, Int_t, Int_t, Int_t, Int_t, Option_t*) const
virtual TClass* IsA() const
virtual Double_t KolmogorovTest(TH1* h2, Option_t* option) const
virtual void LabelsDeflate(Option_t* axis = "X")
virtual void LabelsInflate(Option_t* axis = "X")
virtual void LabelsOption(Option_t* option = "h", Option_t* axis = "X")
virtual Int_t Merge(TCollection* list)
virtual void Multiply(TF1* h1, Double_t c1 = 1)
virtual void Multiply(const TH1* h1)
virtual void Multiply(const TH1* h1, const TH1* h2, Double_t c1 = 1, Double_t c2 = 1, Option_t* option)
TH1& operator=(const TH1&)
virtual void Paint(Option_t* option)
virtual void Print(Option_t* option) const
virtual void PutStats(Stat_t* stats)
virtual TH1* Rebin(Int_t ngroup = 2, const char* newname)
virtual void RebinAxis(Axis_t x, Option_t* axis = "X")
virtual void Rebuild(Option_t* option)
virtual void RecursiveRemove(TObject* obj)
virtual void Reset(Option_t* option)
virtual void SavePrimitive(ofstream& out, Option_t* option)
virtual void Scale(Double_t c1 = 1)
virtual void SetAxisColor(Color_t color = 1, Option_t* axis = "X")
virtual void SetAxisRange(Axis_t xmin, Axis_t xmax, Option_t* axis = "X")
virtual void SetBarOffset(Float_t offset = 0.25)
virtual void SetBarWidth(Float_t width = 0.5)
virtual void SetBinContent(Int_t bin, Stat_t content)
virtual void SetBinContent(Int_t binx, Int_t biny, Stat_t content)
virtual void SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
virtual void SetBinError(Int_t bin, Stat_t error)
virtual void SetBinError(Int_t binx, Int_t biny, Stat_t error)
virtual void SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
virtual void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
virtual void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
virtual void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
virtual void SetBinsLength(Int_t = -1)
virtual void SetBuffer(Int_t buffersize, Option_t* option)
virtual void SetCellContent(Int_t binx, Int_t biny, Stat_t content)
virtual void SetCellError(Int_t binx, Int_t biny, Stat_t content)
virtual void SetContent(const Stat_t* content)
virtual void SetContour(Int_t nlevels, const Double_t* levels = 0)
virtual void SetContourLevel(Int_t level, Double_t value)
static void SetDefaultBufferSize(Int_t buffersize = 1000)
virtual void SetDirectory(TDirectory* dir)
virtual void SetEntries(Stat_t n)
virtual void SetError(const Stat_t* error)
virtual void SetLabelColor(Color_t color = 1, Option_t* axis = "X")
virtual void SetLabelFont(Style_t font = 62, Option_t* axis = "X")
virtual void SetLabelOffset(Float_t offset = 0.005, Option_t* axis = "X")
virtual void SetLabelSize(Float_t size = 0.02, Option_t* axis = "X")
virtual void SetMaximum(Double_t maximum = -1111)
virtual void SetMinimum(Double_t minimum = -1111)
virtual void SetName(const char* name)
virtual void SetNameTitle(const char* name, const char* title)
virtual void SetNdivisions(Int_t n = 510, Option_t* axis = "X")
virtual void SetNormFactor(Double_t factor = 1)
virtual void SetOption(Option_t* option = " ")
virtual void SetStats(Bool_t stats = kTRUE)
virtual void SetTickLength(Float_t length = 0.02, Option_t* axis = "X")
virtual void SetTitle(const char* title)
virtual void SetTitleOffset(Float_t offset = 1, Option_t* axis = "X")
virtual void SetTitleSize(Float_t size = 0.02, Option_t* axis = "X")
virtual void SetXTitle(const char* title)
virtual void SetYTitle(const char* title)
virtual void SetZTitle(const char* title)
virtual void ShowMembers(TMemberInspector& insp, char* parent)
virtual void Smooth(Int_t ntimes = 1, Int_t firstbin = -1, Int_t lastbin = -1)
static void SmoothArray(Int_t NN, Double_t* XX, Int_t ntimes = 1)
static void StatOverflows(Bool_t flag = kTRUE)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
virtual void Sumw2()
virtual void UseCurrentStyle()
protected:
Int_t fNcells number of bins(1D), cells (2D) +U/Overflows
TAxis fXaxis X axis descriptor
TAxis fYaxis Y axis descriptor
TAxis fZaxis Z axis descriptor
Short_t fBarOffset (1000*offset) for bar charts or legos
Short_t fBarWidth (1000*width) for bar charts or legos
Stat_t fEntries Number of entries
Stat_t fTsumw Total Sum of weights
Stat_t fTsumw2 Total Sum of squares of weights
Stat_t fTsumwx Total Sum of weight*X
Stat_t fTsumwx2 Total Sum of weight*X*X
Double_t fMaximum Maximum value for plotting
Double_t fMinimum Minimum value for plotting
Double_t fNormFactor Normalization factor
TArrayD fContour Array to display contour levels
TArrayD fSumw2 Array of sum of squares of weights
TString fOption histogram options
TList* fFunctions ->Pointer to list of functions (fits and user)
Int_t fBufferSize fBuffer size
Double_t* fBuffer [fBufferSize] entry buffer
TDirectory* fDirectory !Pointer to directory holding this histogram
Int_t fDimension !Histogram dimension (1, 2 or 3 dim)
Double_t* fIntegral !Integral of bins used by GetRandom
TVirtualHistPainter* fPainter !pointer to histogram painter
static Int_t fgBufferSize !default buffer size for automatic histograms
static Bool_t fgAddDirectory !flag to add histograms to the directory
static Bool_t fgStatOverflows !flag to use under/overflows in statistics
public:
static const enum TH1:: kNoStats
static const enum TH1:: kUserContour
static const enum TH1:: kCanRebin
static const enum TH1:: kLogX
static const enum TH1:: kIsZoomed
static const enum TH1:: kNoTitle
The H I S T O G R A M Classes
===============================
ROOT supports the following histogram types:
1-D histograms:
TH1C : histograms with one byte per channel. Maximum bin content = 255
TH1S : histograms with one short per channel. Maximum bin content = 65535
TH1I : histograms with one int per channel. Maximum bin content = 2147483647
TH1F : histograms with one float per channel. Maximum precision 7 digits
TH1D : histograms with one double per channel. Maximum precision 14 digits
2-D histograms:
TH2C : histograms with one byte per channel. Maximum bin content = 255
TH2S : histograms with one short per channel. Maximum bin content = 65535
TH2I : histograms with one int per channel. Maximum bin content = 2147483647
TH2F : histograms with one float per channel. Maximum precision 7 digits
TH2D : histograms with one double per channel. Maximum precision 14 digits
3-D histograms:
TH3C : histograms with one byte per channel. Maximum bin content = 255
TH3S : histograms with one short per channel. Maximum bin content = 65535
TH3I : histograms with one int per channel. Maximum bin content = 2147483647
TH3F : histograms with one float per channel. Maximum precision 7 digits
TH3D : histograms with one double per channel. Maximum precision 14 digits
Profile histograms: See classes TProfile and TProfile2D
Profile histograms are used to display the mean value of Y and its RMS
for each bin in X. Profile histograms are in many cases an elegant
replacement of two-dimensional histograms : the inter-relation of two
measured quantities X and Y can always be visualized by a two-dimensional
histogram or scatter-plot; If Y is an unknown (but single-valued)
approximate function of X, this function is displayed by a profile
histogram with much better precision than by a scatter-plot.
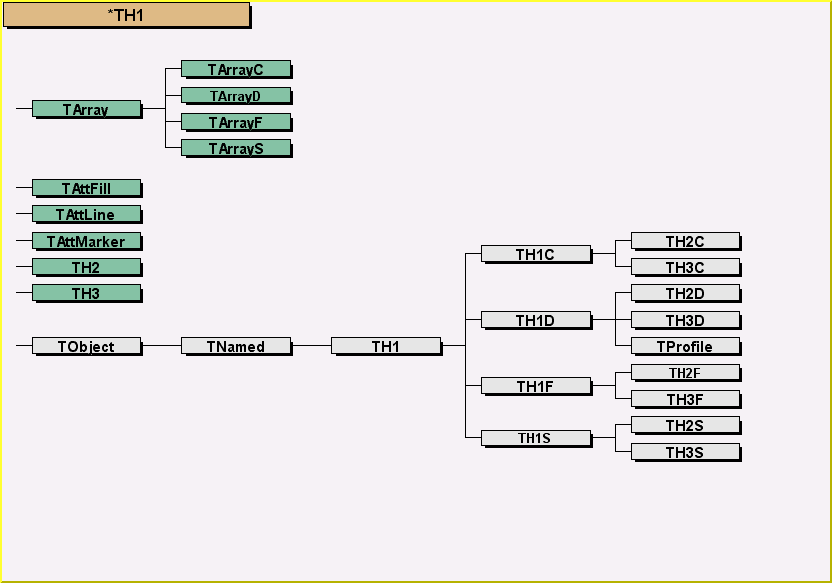
- All histogram classes are derived from the base class TH1
TH1
^
|
|
|
-----------------------------------------------------------
| | | | | | |
| | TH1C TH1S TH1I TH1F TH1D
| | |
| | |
| TH2 TProfile
| |
| |
| ----------------------------------
| | | | | |
| TH2C TH2S TH2I TH2F TH2D
| |
TH3 |
| TProfile2D
|
-------------------------------------
| | | | |
TH3C TH3S TH3I TH3F TH3D
The TH*C classes also inherit from the array class TArrayC.
The TH*S classes also inherit from the array class TArrayS.
The TH*I classes also inherit from the array class TArrayI.
The TH*F classes also inherit from the array class TArrayF.
The TH*D classes also inherit from the array class TArrayD.
Creating histograms
===================
Histograms are created by invoking one of the constructors, eg
TH1F *h1 = new TH1F("h1","h1 title",100,0,4.4);
TH2F *h2 = new TH2F("h2","h2 title",40,0,4,30,-3,3);
histograms may also be created by:
- calling the Clone function, see below
- making a projection from a 2-D or 3-D histogram, see below
- reading an histogram from a file
When an histogram is created, a reference to it is automatically added
to the list of in-memory objects for the current file or directory.
This default behaviour can be changed by:
h->SetDirectory(0); // for the current histogram h
TH1::AddDirectory(kFALSE); // sets a global switch disabling the reference
When the histogram is deleted, the reference to it is removed from
the list of objects in memory.
When a file is closed, all histograms in memory associated with this file
are automatically deleted.
Fix or variable bin size
========================
All histogram types support either fix or variable bin sizes.
2-D histograms may have fix size bins along X and variable size bins
along Y or vice-versa. The functions to fill, manipulate, draw or access
histograms are identical in both cases.
Each histogram always contains 3 objects TAxis: fXaxis, fYaxis and fZaxis
To access the axis parameters, do:
TAxis *xaxis = h->GetXaxis(); etc.
Double_t binCenter = xaxis->GetBinCenter(bin), etc.
See class TAxis for a description of all the access functions.
The axis range is always stored internally in double precision.
Convention for numbering bins
=============================
For all histogram types: nbins, xlow, xup
bin = 0; underflow bin
bin = 1; first bin with low-edge xlow INCLUDED
bin = nbins; last bin with upper-edge xup EXCLUDED
bin = nbins+1; overflow bin
In case of 2-D or 3-D histograms, a "global bin" number is defined.
For example, assuming a 3-D histogram with binx,biny,binz, the function
Int_t gbin = h->GetBin(binx,biny,binz);
returns a global/linearized gbin number. This global gbin is useful
to access the bin content/error information independently of the dimension.
Note that to access the information other than bin content and errors
one should use the TAxis object directly with eg:
Double_t xcenter = h3->GetZaxis()->GetBinCenter(27);
returns the center along z of bin number 27 (not the global bin)
in the 3-d histogram h3.
Alphanumeric Bin Labels
=======================
By default, an histogram axis is drawn with its numeric bin labels.
One can specify alphanumeric labels instead with:
1- call TAxis::SetBinLabel(bin,label);
This can always be done before or after filling.
When the histogram is drawn, bin labels will be automatically drawn.
See example in $ROOTSYS/tutorials/labels1.C, labels2.C
2- call to a Fill function with one of the arguments being a string, eg
hist1->Fill(somename,weigth);
hist2->Fill(x,somename,weight);
hist2->Fill(somename,y,weight);
hist2->Fill(somenamex,somenamey,weight);
See example in $ROOTSYS/tutorials/hlabels1.C, hlabels2.C
3- via TTree::Draw.
see for example $ROOTSYS/tutorials/cern.C
tree.Draw("Nation::Division"); where "Nation" and "Division"
are two branches of a Tree.
When using the options 2 or 3 above, the labels are automatically
added to the list (THashList) of labels for a given axis.
By default, an axis is drawn with the order of bins corresponding
to the filling sequence. It is possible to reorder the axis
- alphabetically
- by increasing or decreasing values
The reordering can be triggered via the TAxis contextMenu by selecting
the menu item "LabelsOption" or by calling directly
TH1::LabelsOption(option,axis) where
-axis may be "X","Y" or "Z"
-option may be:
option = "a" sort by alphabetic order
= ">" sort by decreasing values
= "<" sort by increasing values
= "h" draw labels horizonthal
= "v" draw labels vertical
= "u" draw labels up (end of label right adjusted)
= "d" draw labels down (start of label left adjusted)
When using the option 2 above, new labels are added by doubling the current
number of bins in case one label does not exist yet.
When the Filling is terminated, it is possible to trim the number
of bins to match the number of active labels by calling
TH1::LabelsDeflate(axis) with axis = "X","Y" or "Z"
This operation is automatic when using TTree::Draw.
Once bin labels have been created, they become persistent if the histogram
is written to a file or when generating the C++ code via SavePrimitive.
Histograms with automatic bins
==============================
When an histogram is created with an axis lower limit greater or equal
to its upper limit, the SetBuffer is automatically called with an
argument fBufferSize equal to fgBufferSize (default value=1000).
fgBufferSize may be reset via the static function TH1::SetDefaultBufferSize.
The axis limits will be automatically computed when the buffer will
be full or when the function BufferEmpty is called.
Filling histograms
==================
An histogram is typically filled with statements like:
h1->Fill(x);
h1->Fill(x,w); //fill with weight
h2->Fill(x,y)
h2->Fill(x,y,w)
h3->Fill(x,y,z)
h3->Fill(x,y,z,w)
or via one of the Fill functions accepting names described above.
The Fill functions compute the bin number corresponding to the given
x,y or z argument and increment this bin by the given weight.
The Fill functions return the bin number for 1-D histograms or global
bin number for 2-D and 3-D histograms.
If TH1::Sumw2 has been called before filling, the sum of squares of
weights is also stored.
One can also increment directly a bin number via TH1::AddBinContent
or replace the existing content via TH1::SetBinContent.
To access the bin content of a given bin, do:
Double_t binContent = h->GetBinContent(bin);
By default, the bin number is computed using the current axis ranges.
If the automatic binning option has been set via
h->SetBit(TH1::kCanRebin);
then, the Fill Function will automatically extend the axis range to
accomodate the new value specified in the Fill argument. The method
used is to double the bin size until the new value fits in the range,
merging bins two by two. This automatic binning options is extensively
used by the TTree::Draw function when histogramming Tree variables
with an unknown range.
This automatic binning option is supported for 1-d, 2-D and 3-D histograms.
During filling, some statistics parameters are incremented to compute
the mean value and Root Mean Square with the maximum precision.
In case of histograms of type TH1C, TH1S, TH2C, TH2S, TH3C, TH3S
a check is made that the bin contents do not exceed the maximum positive
capacity (127 or 65535). Histograms of all types may have positive
or/and negative bin contents.
Rebinning
=========
At any time, an histogram can be rebinned via TH1::Rebin. This function
returns a new histogram with the rebinned contents.
If bin errors were stored, they are recomputed during the rebinning.
Associated errors
=================
By default, for each bin, the sum of weights is computed at fill time.
One can also call TH1::Sumw2 to force the storage and computation
of the sum of the square of weights per bin.
If Sumw2 has been called, the error per bin is computed as the
sqrt(sum of squares of weights), otherwise the error is set equal
to the sqrt(bin content).
To return the error for a given bin number, do:
Double_t error = h->GetBinError(bin);
Associated functions
====================
One or more object (typically a TF1*) can be added to the list
of functions (fFunctions) associated to each histogram.
When TH1::Fit is invoked, the fitted function is added to this list.
Given an histogram h, one can retrieve an associated function
with: TF1 *myfunc = h->GetFunction("myfunc");
Operations on histograms
========================
Many types of operations are supported on histograms or between histograms
- Addition of an histogram to the current histogram
- Additions of two histograms with coefficients and storage into the current
histogram
- Multiplications and Divisions are supported in the same way as additions.
- The Add, Divide and Multiply functions also exist to add,divide or multiply
an histogram by a function.
If an histogram has associated error bars (TH1::Sumw2 has been called),
the resulting error bars are also computed assuming independent histograms.
In case of divisions, Binomial errors are also supported.
Fitting histograms
==================
Histograms (1-D,2-D,3-D and Profiles) can be fitted with a user
specified function via TH1::Fit. When an histogram is fitted, the
resulting function with its parameters is added to the list of functions
of this histogram. If the histogram is made persistent, the list of
associated functions is also persistent. Given a pointer (see above)
to an associated function myfunc, one can retrieve the function/fit
parameters with calls such as:
Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
Double_t err0 = myfunc->GetParError(0); //error on first parameter
Projections of histograms
========================
One can:
- make a 1-D projection of a 2-D histogram or Profile
see functions TH2::ProjectionX,Y, TH2::ProfileX,Y, TProfile::ProjectionX
- make a 1-D, 2-D or profile out of a 3-D histogram
see functions TH3::ProjectionZ, TH3::Project3D.
One can fit these projections via:
TH2::FitSlicesX,Y, TH3::FitSlicesZ.
Random Numbers and histograms
=============================
TH1::FillRandom can be used to randomly fill an histogram using
the contents of an existing TF1 function or another
TH1 histogram (for all dimensions).
For example the following two statements create and fill an histogram
10000 times with a default gaussian distribution of mean 0 and sigma 1:
TH1F h1("h1","histo from a gaussian",100,-3,3);
h1.FillRandom("gaus",10000);
TH1::GetRandom can be used to return a random number distributed
according the contents of an histogram.
Making a copy of an histogram
=============================
Like for any other ROOT object derived from TObject, one can use
the Clone() function. This makes an identical copy of the original
histogram including all associated errors and functions, e.g.:
TH1F *hnew = (TH1F*)h->Clone("hnew");
Normalizing histograms
======================
One can scale an histogram such that the bins integral is equal to
the normalization parameter via TH1::Scale(Double_t norm).
Drawing histograms
==================
Histograms are drawn via the THistPainter class. Each histogram has
a pointer to its own painter (to be usable in a multithreaded program).
Many drawing options are supported.
See THistPainter::Paint() for more details.
The same histogram can be drawn with different options in different pads.
When an histogram drawn in a pad is deleted, the histogram is
automatically removed from the pad or pads where it was drawn.
If an histogram is drawn in a pad, then filled again, the new status
of the histogram will be automatically shown in the pad next time
the pad is updated. One does not need to redraw the histogram.
To draw the current version of an histogram in a pad, one can use
h->DrawCopy();
This makes a clone (see Clone below) of the histogram. Once the clone
is drawn, the original histogram may be modified or deleted without
affecting the aspect of the clone.
One can use TH1::SetMaximum() and TH1::SetMinimum() to force a particular
value for the maximum or the minimum scale on the plot.
TH1::UseCurrentStyle() can be used to change all histogram graphics
attributes to correspond to the current selected style.
This function must be called for each histogram.
In case one reads and draws many histograms from a file, one can force
the histograms to inherit automatically the current graphics style
by calling before gROOT->ForceStyle().
Setting Drawing histogram contour levels (2-D hists only)
=========================================================
By default contours are automatically generated at equidistant
intervals. A default value of 20 levels is used. This can be modified
via TH1::SetContour() or TH1::SetContourLevel().
the contours level info is used by the drawing options "cont", "surf",
and "lego".
Setting histogram graphics attributes
=====================================
The histogram classes inherit from the attribute classes:
TAttLine, TAttFill, TAttMarker and TAttText.
See the member functions of these classes for the list of options.
Giving titles to the X, Y and Z axis
====================================
h->GetXaxis()->SetTitle("X axis title");
h->GetYaxis()->SetTitle("Y axis title");
The histogram title and the axis titles can be any TLatex string.
The titles are part of the persistent histogram.
It is also possible to specify the histogram title and the axis
titles at creation time. These titles can be given in the "title"
parameter. They must be separated by ";":
TH1F* h=new TH1F("h","Histogram title;X Axis;Y Axis;Z Axis",100,0,1);
Any title can be omitted:
TH1F* h=new TH1F("h","Histogram title;;Y Axis",100,0,1);
TH1F* h=new TH1F("h",";;Y Axis",100,0,1);
The method SetTitle has the same syntax:
h->SetTitle("Histogram title;An other X title Axis");
Saving/Reading histograms to/from a ROOT file
=============================================
The following statements create a ROOT file and store an histogram
on the file. Because TH1 derives from TNamed, the key identifier on
the file is the histogram name:
TFile f("histos.root","new");
TH1F h1("hgaus","histo from a gaussian",100,-3,3);
h1.FillRandom("gaus",10000);
h1->Write();
To Read this histogram in another Root session, do:
TFile f("histos.root");
TH1F *h = (TH1F*)f.Get("hgaus");
One can save all histograms in memory to the file by:
file->Write();
Miscelaneous operations
=======================
TH1::KolmogorovTest(): statistical test of compatibility in shape
between two histograms
TH1::Smooth() smooths the bin contents of a 1-d histogram
TH1::Integral() returns the integral of bin contents in a given bin range
TH1::GetMean(int axis) returns the mean value along axis
TH1::GetRMS(int axis) returns the sigma distribution along axis
TH1::GetEntries() returns the number of entries
TH1::Reset() resets the bin contents and errors of an histogram
/*
 */
*/
TH1(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
-*-*-*-*-*-*-*-*-*Histogram default constructor*-*-*-*-*-*-*-*-*-*-*-*-*
=============================
~TH1()
-*-*-*-*-*-*-*-*-*Histogram default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*
============================
TH1(const char *name,const char *title,Int_t nbins,Axis_t xlow,Axis_t xup)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
-*-*-*-*-*-*-*Normal constructor for fix bin size histograms*-*-*-*-*-*-*
==============================================
Creates the main histogram structure:
name : name of histogram (avoid blanks)
title : histogram title
if title is of the form "stringt;stringx;stringy;stringz"
the histogram title is set to stringt,
the x axis title to stringy, the y axis title to stringy,etc
nbins : number of bins
xlow : low edge of first bin
xup : upper edge of last bin (not included in last bin)
When an histogram is created, it is automatically added to the list
of special objects in the current directory.
To find the pointer to this histogram in the current directory
by its name, do:
TH1F *h1 = (TH1F*)gDirectory->FindObject(name);
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TH1(const char *name,const char *title,Int_t nbins,const Float_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
-*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
===================================================
Creates the main histogram structure:
name : name of histogram (avoid blanks)
title : histogram title
if title is of the form "stringt;stringx;stringy;stringz"
the histogram title is set to stringt,
the x axis title to stringy, the y axis title to stringy,etc
nbins : number of bins
xbins : array of low-edges for each bin
This is an array of size nbins+1
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TH1(const char *name,const char *title,Int_t nbins,const Double_t *xbins)
:TNamed(name,title), TAttLine(), TAttFill(), TAttMarker()
-*-*-*-*-*Normal constructor for variable bin size histograms*-*-*-*-*-*-*
===================================================
Creates the main histogram structure:
name : name of histogram (avoid blanks)
title : histogram title
if title is of the form "stringt;stringx;stringy;stringz"
the histogram title is set to stringt,
the x axis title to stringy, the y axis title to stringy,etc
nbins : number of bins
xbins : array of low-edges for each bin
This is an array of size nbins+1
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TH1(const TH1 &h) : TNamed(), TAttLine(), TAttFill(), TAttMarker()
Copy constructor.
The list of functions is not copied. (Use Clone if needed)
Bool_t AddDirectoryStatus()
static function: cannot be inlined on Windows/NT
void Browse(TBrowser *b)
void Build()
-*-*-*-*-*-*-*-*Creates histogram basic data structure*-*-*-*-*-*-*-*-*-*
======================================
void Add(TF1 *f1, Double_t c1, Option_t *option)
Performs the operation: this = this + c1*f1
if errors are defined (see TH1::Sumw2), errors are also recalculated.
By default, the function is computed at the centre of the bin.
if option "I" is specified (1-d histogram only), the integral of the
function in each bin is used instead of the value of the function at
the centre of the bin.
Only bins inside the function range are recomputed.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Add
void Add(const TH1 *h1, Double_t c1)
Performs the operation: this = this + c1*h1
if errors are defined (see TH1::Sumw2), errors are also recalculated.
Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
if not already set.
IMPORTANT NOTE1: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Add
IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor
is used , ie this = this + c1*factor*h1
Use the other TH1::Add function if you do not want this feature
void Add(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2)
-*-*-*Replace contents of this histogram by the addition of h1 and h2*-*-*
===============================================================
this = c1*h1 + c2*h2
if errors are defined (see TH1::Sumw2), errors are also recalculated
Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
if not already set.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Add
void AddBinContent(Int_t)
-*-*-*-*-*-*-*-*Increment bin content by 1*-*-*-*-*-*-*-*-*-*-*-*-*-*
==========================
void AddBinContent(Int_t, Stat_t)
-*-*-*-*-*-*-*-*Increment bin content by a weight w*-*-*-*-*-*-*-*-*-*-*
===================================
void AddDirectory(Bool_t add)
Sets the flag controlling the automatic add of histograms in memory
By default (fAddDirectory = kTRUE), histograms are automatically added
to the list of objects in memory.
Note that one histogram can be removed from its support directory
by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it
to the list of objects in the directory dir.
NOTE that this is a static function. To call it, use;
TH1::AddDirectory
Int_t BufferEmpty(Int_t action)
Fill histogram with all entries in the buffer.
action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
action = 0 histogram is filled from the buffer
action = 1 histogram is filled and buffer is deleted
The buffer is automatically deleted when the number of entries
in the buffer is greater than the number of entries in the histogram
Int_t BufferFill(Axis_t x, Stat_t w)
accumulate arguments in buffer. When buffer is full, empty the buffer
fBuffer[0] = number of entries in buffer
fBuffer[1] = w of first entry
fBuffer[2] = x of first entry
Double_t Chi2Test(TH1 *h, Option_t *option, Int_t constraint)
The Chi2 (Pearson's) test for differences between h and this histogram.
a small value of prob indicates a significant difference between the distributions
if the data was collected in such a way that the number of entries
in the first histogram is necessarily equal to the number of entries
in the second, the parameter _constraint_ must be made 1. Default is 0.
any additional constraints on the data lower the number of degrees of freedom
(i.e. increase constraint to more positive values) in accordance with
their number
/options:
"O" -overflows included
"U" - underflows included
"P" - print information about number of degrees of freedom and
the value of chi2
by default underflows and overflows are not included
Double_t ComputeIntegral()
Compute integral (cumulative sum of bins)
The result stored in fIntegral is used by the GetRandom functions.
This function is automatically called by GetRandom when the fIntegral
array does not exist or when the number of entries in the histogram
has changed since the previous call to GetRandom.
The resulting integral is normalized to 1
void Copy(TObject &obj) const
-*-*-*-*-*Copy this histogram structure to newth1*-*-*-*-*-*-*-*-*-*-*-*
=======================================
Note that this function does not copy the list of associated functions.
Use TObJect::Clone to make a full copy of an histogram.
Int_t DistancetoPrimitive(Int_t px, Int_t py)
-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a line*-*-*-*-*-*
===========================================
Compute the closest distance of approach from point px,py to elements
of an histogram.
The distance is computed in pixels units.
Algorithm:
Currently, this simple model computes the distance from the mouse
to the histogram contour only.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void Divide(TF1 *f1, Double_t c1)
Performs the operation: this = this/(c1*f1)
if errors are defined (see TH1::Sumw2), errors are also recalculated.
Only bins inside the function range are recomputed.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Divide
void Divide(const TH1 *h1)
-*-*-*-*-*-*-*-*-*Divide this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
===========================
this = this/h1
if errors are defined (see TH1::Sumw2), errors are also recalculated.
Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
if not already set.
The resulting errors are calculated assuming uncorrelated histograms.
See the other TH1::Divide that gives the possibility to optionaly
compute Binomial errors.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Scale
void Divide(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
-*-*-*Replace contents of this histogram by the division of h1 by h2*-*-*
==============================================================
this = c1*h1/(c2*h2)
if errors are defined (see TH1::Sumw2), errors are also recalculated
Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
if not already set.
The resulting errors are calculated assuming uncorrelated histograms.
However, if option ="B" is specified, Binomial errors are computed.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Divide
void Draw(Option_t *option)
-*-*-*-*-*-*-*-*-*Draw this histogram with options*-*-*-*-*-*-*-*-*-*-*-*
================================
Histograms are drawn via the THistPainter class. Each histogram has
a pointer to its own painter (to be usable in a multithreaded program).
The same histogram can be drawn with different options in different pads.
When an histogram drawn in a pad is deleted, the histogram is
automatically removed from the pad or pads where it was drawn.
If an histogram is drawn in a pad, then filled again, the new status
of the histogram will be automatically shown in the pad next time
the pad is updated. One does not need to redraw the histogram.
To draw the current version of an histogram in a pad, one can use
h->DrawCopy();
This makes a clone of the histogram. Once the clone is drawn, the original
histogram may be modified or deleted without affecting the aspect of the
clone.
By default, TH1::Draw clears the current pad.
One can use TH1::SetMaximum and TH1::SetMinimum to force a particular
value for the maximum or the minimum scale on the plot.
TH1::UseCurrentStyle can be used to change all histogram graphics
attributes to correspond to the current selected style.
This function must be called for each histogram.
In case one reads and draws many histograms from a file, one can force
the histograms to inherit automatically the current graphics style
by calling before gROOT->ForceStyle();
See THistPainter::Paint for a description of all the drawing options
=======================
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TH1* DrawCopy(Option_t *) const
-*-*-*-*-*Copy this histogram and Draw in the current pad*-*-*-*-*-*-*-*
===============================================
Once the histogram is drawn into the pad, any further modification
using graphics input will be made on the copy of the histogram,
and not to the original object.
See Draw for the list of options
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TH1* DrawNormalized(Option_t *option, Double_t norm) const
Draw a normalized copy of this histogram.
A clone of this histogram is normalized to norm and drawn with option.
A pointer to the normalized histogram is returned.
The contents of the histogram copy are scaled such that the new
sum of weights (excluding under and overflow) is equal to norm.
Note that the returned normalized histogram is not added to the list
of histograms in the current directory in memory.
It is the user's responsability to delete this histogram.
The kCanDelete bit is set for the returned object. If a pad containing
this copy is cleared, the histogram will be automatically deleted.
See Draw for the list of options
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void DrawPanel()
-*-*-*-*-*Display a panel with all histogram drawing options*-*-*-*-*-*
==================================================
See class TDrawPanelHist for example
void Eval(TF1 *f1, Option_t *option)
-*-*-*Evaluate function f1 at the center of bins of this histogram-*-*-*-*
============================================================
If option "R" is specified, the function is evaluated only
for the bins included in the function range.
If option "A" is specified, the value of the function is added to the
existing bin contents
If option "S" is specified, the value of the function is used to
generate a value, distributed according to the Poisson
distribution, with f1 as the mean.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void ExecuteEvent(Int_t event, Int_t px, Int_t py)
-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
=========================================
This member function is called when a histogram is clicked with the locator
If Left button clicked on the bin top value, then the content of this bin
is modified according to the new position of the mouse when it is released.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t Fill(Axis_t x)
-*-*-*-*-*-*-*-*Increment bin with abscissa X by 1*-*-*-*-*-*-*-*-*-*-*
==================================
if x is less than the low-edge of the first bin, the Underflow bin is incremented
if x is greater than the upper edge of last bin, the Overflow bin is incremented
If the storage of the sum of squares of weights has been triggered,
via the function Sumw2, then the sum of the squares of weights is incremented
by 1 in the bin corresponding to x.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t Fill(Axis_t x, Stat_t w)
-*-*-*-*-*-*Increment bin with abscissa X with a weight w*-*-*-*-*-*-*-*
=============================================
if x is less than the low-edge of the first bin, the Underflow bin is incremented
if x is greater than the upper edge of last bin, the Overflow bin is incremented
If the storage of the sum of squares of weights has been triggered,
via the function Sumw2, then the sum of the squares of weights is incremented
by w^2 in the bin corresponding to x.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Int_t Fill(const char *namex, Stat_t w)
Increment bin with namex with a weight w
if x is less than the low-edge of the first bin, the Underflow bin is incremented
if x is greater than the upper edge of last bin, the Overflow bin is incremented
If the storage of the sum of squares of weights has been triggered,
via the function Sumw2, then the sum of the squares of weights is incremented
by w^2 in the bin corresponding to x.
void FillN(Int_t ntimes, const Axis_t *x, const Double_t *w, Int_t stride)
-*-*-*-*-*-*Fill this histogram with an array x and weights w*-*-*-*-*
=================================================
ntimes: number of entries in arrays x and w (array size must be ntimes*stride)
x: array of values to be histogrammed
w: array of weighs
stride: step size through arrays x and w
If the storage of the sum of squares of weights has been triggered,
via the function Sumw2, then the sum of the squares of weights is incremented
by w[i]^2 in the bin corresponding to x[i].
if w is NULL each entry is assumed a weight=1
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void FillRandom(const char *fname, Int_t ntimes)
-*-*-*-*-*Fill histogram following distribution in function fname*-*-*-*
=======================================================
The distribution contained in the function fname (TF1) is integrated
over the channel contents.
It is normalized to 1.
Getting one random number implies:
- Generating a random number between 0 and 1 (say r1)
- Look in which bin in the normalized integral r1 corresponds to
- Fill histogram channel
ntimes random numbers are generated
One can also call TF1::GetRandom to get a random variate from a function.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
void FillRandom(TH1 *h, Int_t ntimes)
-*-*-*-*-*Fill histogram following distribution in histogram h*-*-*-*
====================================================
The distribution contained in the histogram h (TH1) is integrated
over the channel contents.
It is normalized to 1.
Getting one random number implies:
- Generating a random number between 0 and 1 (say r1)
- Look in which bin in the normalized integral r1 corresponds to
- Fill histogram channel
ntimes random numbers are generated
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Int_t FindBin(Axis_t x, Axis_t y, Axis_t z)
-*-*-*-*Return Global bin number corresponding to x,y,z*-*-*-*-*-*-*
===============================================
2-D and 3-D histograms are represented with a one dimensional
structure.
This has the advantage that all existing functions, such as
GetBinContent, GetBinError, GetBinFunction work for all dimensions.
See also TH1::GetBin
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TObject* FindObject(const char *name) const
search object named name in the list of functions
TObject* FindObject(const TObject *obj) const
search object obj in the list of functions
Int_t Fit(const char *fname ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
Fit histogram with function fname
=================================
fname is the name of an already predefined function created by TF1 or TF2
Predefined functions such as gaus, expo and poln are automatically
created by ROOT.
This function finds a pointer to the TF1 object with name fname
and calls TH1::Fit(TF1 *f1,...)
Int_t Fit(TF1 *f1 ,Option_t *option ,Option_t *goption, Axis_t xxmin, Axis_t xxmax)
Fit histogram with function f1
==============================
Fit this histogram with function f1.
The list of fit options is given in parameter option.
option = "W" Set all errors to 1
= "I" Use integral of function in bin instead of value at bin center
= "L" Use Loglikelihood method (default is chisquare method)
= "LL" Use Loglikelihood method and bin contents are not integers)
= "U" Use a User specified fitting algorithm (via SetFCN)
= "Q" Quiet mode (minimum printing)
= "V" Verbose mode (default is between Q and V)
= "E" Perform better Errors estimation using Minos technique
= "B" Use this option when you want to fix one or more parameters
and the fitting function is like "gaus","expo","poln","landau".
= "M" More. Improve fit results
= "R" Use the Range specified in the function range
= "N" Do not store the graphics function, do not draw
= "0" Do not plot the result of the fit. By default the fitted function
is drawn unless the option"N" above is specified.
= "+" Add this new fitted function to the list of fitted functions
(by default, any previous function is deleted)
When the fit is drawn (by default), the parameter goption may be used
to specify a list of graphics options. See TH1::Draw for a complete
list of these options.
In order to use the Range option, one must first create a function
with the expression to be fitted. For example, if your histogram
has a defined range between -4 and 4 and you want to fit a gaussian
only in the interval 1 to 3, you can do:
TF1 *f1 = new TF1("f1","gaus",1,3);
histo->Fit("f1","R");
Setting initial conditions
==========================
Parameters must be initialized before invoking the Fit function.
The setting of the parameter initial values is automatic for the
predefined functions : poln, expo, gaus, landau. One can however disable
this automatic computation by specifying the option "B".
Note that if a predefined function is defined with an argument,
eg, gaus(0), expo(1), you must specify the initial values for
the parameters.
You can specify boundary limits for some or all parameters via
f1->SetParLimits(p_number, parmin, parmax);
if parmin>=parmax, the parameter is fixed
Note that you are not forced to fix the limits for all parameters.
For example, if you fit a function with 6 parameters, you can do:
func->SetParameters(0,3.1,1.e-6,-8,0,100);
func->SetParLimits(3,-10,-4);
func->FixParameter(4,0);
func->SetParLimits(5, 1,1);
With this setup, parameters 0->2 can vary freely
Parameter 3 has boundaries [-10,-4] with initial value -8
Parameter 4 is fixed to 0
Parameter 5 is fixed to 100.
When the lower limit and upper limit are equal, the parameter is fixed.
However to fix a parameter to 0, one must call the FixParameter function.
Note that option "I" gives better results but is slower.
Changing the fitting function
=============================
By default the fitting function H1FitChisquare is used.
To specify a User defined fitting function, specify option "U" and
call the following functions:
TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)
where MyFittingFunction is of type:
extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
Associated functions
====================
One or more object (typically a TF1*) can be added to the list
of functions (fFunctions) associated to each histogram.
When TH1::Fit is invoked, the fitted function is added to this list.
Given an histogram h, one can retrieve an associated function
with: TF1 *myfunc = h->GetFunction("myfunc");
Access to the fit results
=========================
If the histogram is made persistent, the list of
associated functions is also persistent. Given a pointer (see above)
to an associated function myfunc, one can retrieve the function/fit
parameters with calls such as:
Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
Double_t err0 = myfunc->GetParError(0); //error on first parameter
Access to the fit covariance matrix
===================================
Example1:
TH1F h("h","test",100,-2,2);
h.FillRandom("gaus",1000);
h.Fit("gaus");
Double_t matrix[3][3];
gMinuit->mnemat(&matrix[0][0],3);
Example2:
TH1F h("h","test",100,-2,2);
h.FillRandom("gaus",1000);
h.Fit("gaus");
TVirtualFitter *fitter = TVirtualFitter::GetFitter();
TMatrixD matrix(npar,npar,fitter->GetCovarianceMatrix());
Double_t errorFirstPar = fitter->GetCovarianceMatrixElement(0,0);
Changing the maximum number of parameters
=========================================
By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
You can redefine this default value by calling :
TVirtualFitter::Fitter(0,150); //to get a maximum of 150 parameters
Excluding points
================
Use TF1::RejectPoint inside your fitting function to exclude points
within a certain range from the fit. Example:
Double_t fline(Double_t *x, Double_t *par)
{
if (x[0] > 2.5 && x[0] < 3.5) {
TF1::RejectPoint();
return 0;
}
return par[0] + par[1]*x[0];
}
void exclude() {
TF1 *f1 = new TF1("f1","[0] +[1]*x +gaus(2)",0,5);
f1->SetParameters(6,-1,5,3,0.2);
TH1F *h = new TH1F("h","background + signal",100,0,5);
h->FillRandom("f1",2000);
TF1 *fline = new TF1("fline",fline,0,5,2);
fline->SetParameters(2,-1);
h->Fit("fline","l");
}
Warning when using the option "0"
=================================
When selecting the option "0", the fitted function is added to
the list of functions of the histogram, but it is not drawn.
You can undo what you disabled in the following way:
h.Fit("myFunction","0"); // fit, store function but do not draw
h.Draw(); function is not drawn
const Int_t kNotDraw = 1<<9;
h.GetFunction("myFunction")->ResetBit(kNotDraw);
h.Draw(); // function is visible again
Access to the Fitter information during fitting
===============================================
This function calls only the abstract fitter TVirtualFitter.
The default fitter is TFitter (calls TMinuit).
The default fitter can be set in the resource file in etc/system.rootrc
Root.Fitter: Fumili
A different fitter can also be set via TVirtualFitter::SetDefaultFitter.
For example, to call the "Fumili" fitter instead of "Minuit", do
TVirtualFitter::SetDefaultFitter("Fumili");
During the fitting process, the objective function:
chisquare, likelihood or any user defined algorithm
is called (see eg in the TFitter class, the static functions
H1FitChisquare, H1FitLikelihood).
This objective function, in turn, calls the user theoretical function.
This user function is a static function called from the TF1 *f1 function.
Inside this user defined theoretical function , one can access:
TVirtualFitter *fitter = TVirtualFitter::GetFitter(); //the current fitter
TH1 *hist = (TH1*)fitter->GetObjectFit(); //the histogram being fitted
TF1 +f1 = (TF1*)fitter->GetUserFunction(); //the user theoretical function
By default, the fitter TMinuit is initialized with a maximum of 25 parameters.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void FitPanel()
-*-*-*-*-*Display a panel with all histogram fit options*-*-*-*-*-*
==============================================
See class TFitPanel for example
TH1* GetAsymmetry(TH1* h2, Double_t c2, Double_t dc2)
return an histogram containing the asymmetry of this histogram with h2,
where the asymmetry is defined as:
Asymmetry = (h1 - h2)/(h1 + h2) where h1 = this
works for 1D, 2D, etc. histograms
c2 is an optional argument that gives a relative weight between the two
histograms, and dc2 is the error on this weight. This is useful, for example,
when forming an asymmetry between two histograms from 2 different data sets that
need to be normalized to each other in some way. The function calculates
the errors asumming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).
example: assuming 'h1' and 'h2' are already filled
h3 = h1->GetAsymmetry(h2)
then 'h3' is created and filled with the asymmetry between 'h1' and 'h2';
h1 and h2 are left intact.
Note that it is the user's responsibility to manage the created histogram.
code proposed by Jason Seely (seely@mit.edu) and adapted by R.Brun
clone the histograms so top and bottom will have the
correct dimensions:
Sumw2 just makes sure the errors will be computed properly
when we form sums and ratios below.
Int_t GetDefaultBufferSize()
return the default buffer size for automatic histograms
the parameter fgBufferSize may be changed via SetDefaultBufferSize
Double_t GetEntries() const
return the current number of entries
char* GetObjectInfo(Int_t px, Int_t py) const
Redefines TObject::GetObjectInfo.
Displays the histogram info (bin number, contents, integral up to bin
corresponding to cursor position px,py
TVirtualHistPainter* GetPainter()
return pointer to painter
if painter does not exist, it is created
Int_t GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
Compute Quantiles for this histogram
Quantile x_q of a probability distribution Function F is defined as
F(x_q) = q with 0 <= q <= 1.
For instance the median x_0.5 of a distribution is defined as that value
of the random variable for which the distribution function equals 0.5:
F(x_0.5) = Probability(x < x_0.5) = 0.5
code from Eddy Offermann, Renaissance
input parameters
- this 1-d histogram (TH1F,D,etc). Could also be a TProfile
- nprobSum maximum size of array q and size of array probSum (if given)
- probSum array of positions where quantiles will be computed.
if probSum is null, probSum will be computed internally and will
have a size = number of bins + 1 in h. it will correspond to the
quantiles calculated at the lowest edge of the histogram (quantile=0) and
all the upper edges of the bins.
if probSum is not null, it is assumed to contain at least nprobSum values.
output
- return value nq (<=nprobSum) with the number of quantiles computed
- array q filled with nq quantiles
Note that the Integral of the histogram is automatically recomputed
if the number of entries is different of the number of entries when
the integral was computed last time. In case you do not use the Fill
functions to fill your histogram, but SetBinContent, you must call
TH1::ComputeIntegral before calling this function.
Getting quantiles q from two histograms and storing results in a TGraph,
a so-called QQ-plot
TGraph *gr = new TGraph(nprob);
h1->GetQuantiles(nprob,gr->GetX());
h2->GetQuantiles(nprob,gr->GetY());
gr->Draw("alp");
Example:
void quantiles() {
// demo for quantiles
const Int_t nq = 20;
TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
h->FillRandom("gaus",5000);
Double_t xq[nq]; // position where to compute the quantiles in [0,1]
Double_t yq[nq]; // array to contain the quantiles
for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
h->GetQuantiles(nq,yq,xq);
//show the original histogram in the top pad
TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
c1->Divide(1,2);
c1->cd(1);
h->Draw();
// show the quantiles in the bottom pad
c1->cd(2);
gPad->SetGrid();
TGraph *gr = new TGraph(nq,xq,yq);
gr->SetMarkerStyle(21);
gr->Draw("alp");
}
Int_t FitOptionsMake(Option_t *choptin, Foption_t &Foption)
-*-*-*-*-*-*-*Decode string choptin and fill Foption structure*-*-*-*-*-*
================================================
Int_t GetBin(Int_t binx, Int_t biny, Int_t binz) const
-*-*-*-*Return Global bin number corresponding to binx,y,z*-*-*-*-*-*-*
==================================================
2-D and 3-D histograms are represented with a one dimensional
structure.
This has the advantage that all existing functions, such as
GetBinContent, GetBinError, GetBinFunction work for all dimensions.
In case of a TH1x, returns binx directly.
Convention for numbering bins
=============================
For all histogram types: nbins, xlow, xup
bin = 0; underflow bin
bin = 1; first bin with low-edge xlow INCLUDED
bin = nbins; last bin with upper-edge xup EXCLUDED
bin = nbins+1; overflow bin
In case of 2-D or 3-D histograms, a "global bin" number is defined.
For example, assuming a 3-D histogram with binx,biny,binz, the function
Int_t bin = h->GetBin(binx,biny,binz);
returns a global/linearized bin number. This global bin is useful
to access the bin information independently of the dimension.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Axis_t GetRandom() const
return a random number distributed according the histogram bin contents.
This function checks if the bins integral exists. If not, the integral
is evaluated, normalized to one.
The integral is automatically recomputed if the number of entries
is not the same then when the integral was computed.
NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise.
Stat_t GetBinContent(Int_t) const
-*-*-*-*-*Return content of bin number bin
================================
Implemented in TH1C,S,F,D
Convention for numbering bins
=============================
For all histogram types: nbins, xlow, xup
bin = 0; underflow bin
bin = 1; first bin with low-edge xlow INCLUDED
bin = nbins; last bin with upper-edge xup EXCLUDED
bin = nbins+1; overflow bin
In case of 2-D or 3-D histograms, a "global bin" number is defined.
For example, assuming a 3-D histogram with binx,biny,binz, the function
Int_t bin = h->GetBin(binx,biny,binz);
returns a global/linearized bin number. This global bin is useful
to access the bin information independently of the dimension.
Stat_t GetBinContent(Int_t binx, Int_t biny) const
-*-*-*-*-*Return content of bin number binx, biny
=======================================
NB: Function to be called for 2-d histograms only
see convention for numbering bins in TH1::GetBin
Stat_t GetBinContent(Int_t binx, Int_t biny, Int_t binz) const
-*-*-*-*-*Return content of bin number binx,biny,binz
===========================================
NB: Function to be called for 3-d histograms only
see convention for numbering bins in TH1::GetBin
TAxis* GetXaxis() const
return a pointer to the X axis object
TAxis* GetYaxis() const
return a pointer to the Y axis object
TAxis* GetZaxis() const
return a pointer to the Z axis object
void LabelsDeflate(Option_t *ax)
Reduce the number of bins for this axis to the number of bins having a label.
void LabelsInflate(Option_t *ax)
Double the number of bins for axis.
Refill histogram
This function is called by TAxis::FindBin(const char *label)
void LabelsOption(Option_t *option, Option_t *ax)
Set option(s) to draw axis with labels
option = "a" sort by alphabetic order
= ">" sort by decreasing values
= "<" sort by increasing values
= "h" draw labels horizonthal
= "v" draw labels vertical
= "u" draw labels up (end of label right adjusted)
= "d" draw labels down (start of label left adjusted)
Int_t Merge(TCollection *list)
Add all histograms in the collection to this histogram.
This function computes the min/max for the x axis,
compute a new number of bins, if necessary,
add bin contents, errors and statistics.
If all histograms have bin labels, bins with identical labels
will be merged, no matter what their order is.
The function returns the merged number of entries if the merge is
successfull, -1 otherwise.
IMPORTANT remark. The axis x may have different number
of bins and different limits, BUT the largest bin width must be
a multiple of the smallest bin width.
Example:
void atest() {
TH1F *h1 = new TH1F("h1","h1",110,-110,0);
TH1F *h2 = new TH1F("h2","h2",220,0,110);
TH1F *h3 = new TH1F("h3","h3",330,-55,55);
TRandom r;
for (Int_t i=0;i<10000;i++) {
h1->Fill(r.Gaus(-55,10));
h2->Fill(r.Gaus(55,10));
h3->Fill(r.Gaus(0,10));
}
TList *list = new TList;
list->Add(h1);
list->Add(h2);
list->Add(h3);
TH1F *h = (TH1F*)h1->Clone("h");
h->Reset();
h.Merge(list);
h->Draw();
}
void Multiply(TF1 *f1, Double_t c1)
Performs the operation: this = this*c1*f1
if errors are defined (see TH1::Sumw2), errors are also recalculated.
Only bins inside the function range are recomputed.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Multiply
void Multiply(const TH1 *h1)
-*-*-*-*-*-*-*-*-*Multiply this histogram by h1*-*-*-*-*-*-*-*-*-*-*-*-*
=============================
this = this*h1
If errors of this are available (TH1::Sumw2), errors are recalculated.
Note that if h1 has Sumw2 set, Sumw2 is automatically called for this
if not already set.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Multiply
void Multiply(const TH1 *h1, const TH1 *h2, Double_t c1, Double_t c2, Option_t *option)
-*-*-*Replace contents of this histogram by multiplication of h1 by h2*-*
================================================================
this = (c1*h1)*(c2*h2)
If errors of this are available (TH1::Sumw2), errors are recalculated.
Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this
if not already set.
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Multiply
void Paint(Option_t *option)
-*-*-*-*-*-*-*Control routine to paint any kind of histograms*-*-*-*-*-*-*
===============================================
This function is automatically called by TCanvas::Update.
(see TH1::Draw for the list of options)
TH1* Rebin(Int_t ngroup, const char*newname)
-*-*-*Rebin this histogram grouping ngroup bins together*-*-*-*-*-*-*-*-*
==================================================
if newname is not blank a new temporary histogram hnew is created.
else the current histogram is modified (default)
The parameter ngroup indicates how many bins of this have to me merged
into one bin of hnew
If the original histogram has errors stored (via Sumw2), the resulting
histograms has new errors correctly calculated.
examples: if h1 is an existing TH1F histogram with 100 bins
h1->Rebin(); //merges two bins in one in h1: previous contents of h1 are lost
h1->Rebin(5); //merges five bins in one in h1
TH1F *hnew = h1->Rebin(5,"hnew"); // creates a new histogram hnew
//merging 5 bins of h1 in one bin
NOTE1: If ngroup is not an exact divider of the number of bins,
the top limit of the rebinned histogram is changed
to the upper edge of the bin=newbins*ngroup and the corresponding
bins are added to the overflow bin.
Statistics will be recomputed from the new bin contents.
NOTE2: This function cannot be used with variable bin size histograms.
void RebinAxis(Axis_t x, const char *ax)
Histogram is resized along ax such that x is in the axis range.
The new axis limits are recomputed by doubling iteratively
the current axis range until the specified value x is within the limits.
The algorithm makes a copy of the histogram, then loops on all bins
of the old histogram to fill the rebinned histogram.
Takes into account errors (Sumw2) if any.
The algorithm works for 1-d, 2-d and 3-d histograms.
The bit kCanRebin must be set before invoking this function.
Ex: h->SetBit(TH1::kCanRebin);
void RecursiveRemove(TObject *obj)
Recursively remove object from the list of functions
void Scale(Double_t c1)
-*-*-*Multiply this histogram by a constant c1*-*-*-*-*-*-*-*-*
========================================
this = c1*this
Note that both contents and errors(if any) are scaled.
This function uses the services of TH1::Add
IMPORTANT NOTE: If you intend to use the errors of this histogram later
you should call Sumw2 before making this operation.
This is particularly important if you fit the histogram after TH1::Scale
void SetDefaultBufferSize(Int_t buffersize)
static function to set the default buffer size for automatic histograms.
When an histogram is created with one of its axis lower limit greater
or equal to its upper limit, the function SetBuffer is automatically
called with the default buffer size.
void SetTitle(const char *title)
Change (i.e. set) the title
if title is of the form "stringt;stringx;stringy;stringz"
the histogram title is set to stringt,
the x axis title to stringx, the y axis title to stringy,etc
void SmoothArray(Int_t NN, Double_t *XX, Int_t ntimes)
smooth array XX, translation of Hbook routine hsmoof.F
based on algorithm 353QH twice presented by J. Friedman
in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.
void Smooth(Int_t ntimes, Int_t firstbin, Int_t lastbin)
Smooth bin contents of this histogram between firstbin and lastbin.
(if firstbin=-1 and lastbin=-1 (default) all bins are smoothed.
bin contents are replaced by their smooth values.
Errors (if any) are not modified.
algorithm can only be applied to 1-d histograms
void StatOverflows(Bool_t flag)
if flag=kTRUE, underflows and overflows are used by the Fill functions
in the computation of statistics (mean value, RMS).
By default, underflows or overflows are not used.
void Streamer(TBuffer &b)
-*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
=====================
void Print(Option_t *option) const
-*-*-*-*-*Print some global quantities for this histogram*-*-*-*-*-*-*-*
===============================================
If option "base" is given, number of bins and ranges are also printed
If option "range" is given, bin contents and errors are also printed
for all bins in the current range (default 1-->nbins)
If option "all" is given, bin contents and errors are also printed
for all bins including under and overflows.
void Rebuild(Option_t *)
Using the current bin info, recompute the arrays for contents and errors
void Reset(Option_t *option)
-*-*-*-*-*-*Reset this histogram: contents, errors, etc*-*-*-*-*-*-*-*
===========================================
if option "ICE" is specified, resets only Integral, Contents and Errors.
void SavePrimitive(ofstream &out, Option_t *option)
Save primitive as a C++ statement(s) on output stream out
void SavePrimitiveHelp(ofstream &out, Option_t *option)
helper function for the SavePrimitive functions from TH1
or classes derived from TH1, eg TProfile, TProfile2D.
void UseCurrentStyle()
-*-*-*-*Replace current attributes by current style*-*-*-*-*
===========================================
Double_t GetMean(Int_t axis) const
-*-*-*-*-*-*Return mean value of this histogram along the X axis*-*-*-*-*
====================================================
Note that the mean value/RMS is computed using the bins in the currently
defined range (see TAxis::SetRange). By default the range includes
all bins from 1 to nbins included, excluding underflows and overflows.
To force the underflows and overflows in the computation, one must
call the static function TH1::StatOverflows(kTRUE) before filling
the histogram.
Double_t GetMeanError(Int_t axis) const
-*-*-*-*-*-*Return standard error of mean of this histogram along the X axis*-*-*-*-*
====================================================
Note that the mean value/RMS is computed using the bins in the currently
defined range (see TAxis::SetRange). By default the range includes
all bins from 1 to nbins included, excluding underflows and overflows.
To force the underflows and overflows in the computation, one must
call the static function TH1::StatOverflows(kTRUE) before filling
the histogram.
Also note, that although the definition of standard error doesn't include the
assumption of normality, many uses of this feature implicitly assume it.
Double_t GetRMS(Int_t axis) const
Return the Sigma value of this histogram
Note that the mean value/sigma is computed using the bins in the currently
defined range (see TAxis::SetRange). By default the range includes
all bins from 1 to nbins included, excluding underflows and overflows.
To force the underflows and overflows in the computation, one must
call the static function TH1::StatOverflows(kTRUE) before filling
the histogram.
Note that this function returns the Standard Deviation (Sigma)
of the distribution (not RMS).
The Sigma estimate is computed as Sqrt((1/N)*(Sum(x_i-x_mean)^2))
The name "RMS" was introduced many years ago (Hbook/PAW times).
We kept the name for continuity.
Double_t GetRMSError(Int_t axis) const
Return error of RMS estimation for Normal distribution
Note that the mean value/RMS is computed using the bins in the currently
defined range (see TAxis::SetRange). By default the range includes
all bins from 1 to nbins included, excluding underflows and overflows.
To force the underflows and overflows in the computation, one must
call the static function TH1::StatOverflows(kTRUE) before filling
the histogram.
Value returned is standard deviation of sample standard deviation.
void GetStats(Stat_t *stats) const
fill the array stats from the contents of this histogram
The array stats must be correctly dimensionned in the calling program.
stats[0] = sumw
stats[1] = sumw2
stats[2] = sumwx
stats[3] = sumwx2
If no axis-subrange is specified (via TAxis::SetRange), the array stats
is simply a copy of the statistics quantities computed at filling time.
If a sub-range is specified, the function recomputes these quantities
from the bin contents in the current axis range.
Note that the mean value/RMS is computed using the bins in the currently
defined range (see TAxis::SetRange). By default the range includes
all bins from 1 to nbins included, excluding underflows and overflows.
To force the underflows and overflows in the computation, one must
call the static function TH1::StatOverflows(kTRUE) before filling
the histogram.
void PutStats(Stat_t *stats)
Replace current statistics with the values in array stats
Stat_t GetSumOfWeights() const
-*-*-*-*-*-*Return the sum of weights excluding under/overflows*-*-*-*-*
===================================================
Stat_t Integral(Option_t *option) const
Return integral of bin contents. Only bins in the bins range are considered.
By default the integral is computed as the sum of bin contents in the range.
if option "width" is specified, the integral is the sum of
the bin contents multiplied by the bin width in x.
Stat_t Integral(Int_t binx1, Int_t binx2, Option_t *option) const
Return integral of bin contents between binx1 and binx2 for a 1-D histogram
By default the integral is computed as the sum of bin contents in the range.
if option "width" is specified, the integral is the sum of
the bin contents multiplied by the bin width in x.
Double_t KolmogorovTest(TH1 *h2, Option_t *option) const
Statistical test of compatibility in shape between
THIS histogram and h2, using Kolmogorov test.
Default: Ignore under- and overflow bins in comparison
option is a character string to specify options
"U" include Underflows in test (also for 2-dim)
"O" include Overflows (also valid for 2-dim)
"N" include comparison of normalizations
"D" Put out a line of "Debug" printout
"M" Return the Maximum Kolmogorov distance instead of prob
"X" Run the pseudo experiments post-processor with the following procedure:
make pseudoexperiments based on random values from the parent
distribution and compare the KS distance of the pseudoexperiment
to the parent distribution. Bin the KS distances in a histogram,
and then take the integral of all the KS values above the value
obtained from the original data to Monte Carlo distribution.
The number of pseudo-experiments NEXPT is currently fixed at 1000.
The function returns the integral.
(thanks to Ben Kilminster to submit this procedure). Note that
this option "X" is much slower.
The returned function value is the probability of test
(much less than one means NOT compatible)
Code adapted by Rene Brun from original HBOOK routine HDIFF
void SetContent(const Stat_t *content)
-*-*-*-*-*-*Replace bin contents by the contents of array content*-*-*-*
=====================================================
Int_t GetContour(Double_t *levels)
Return contour values into array levels if pointer levels is non zero
The function returns the number of contour levels.
see GetContourLevel to return one contour only
Double_t GetContourLevel(Int_t level) const
Return value of contour number level
see GetContour to return the array of all contour levels
Double_t GetContourLevelPad(Int_t level) const
Return the value of contour number "level" in Pad coordinates ie: if the Pad
is in log scale along Z it returns le log of the contour level value.
see GetContour to return the array of all contour levels
void SetBuffer(Int_t buffersize, Option_t * /*option*/)
set the maximum number of entries to be kept in the buffer
void SetContour(Int_t nlevels, const Double_t *levels)
-*-*-*-*-*-*Set the number and values of contour levels*-*-*-*-*-*-*-*-*
===========================================
By default the number of contour levels is set to 20.
if argument levels = 0 or missing, equidistant contours are computed
void SetContourLevel(Int_t level, Double_t value)
-*-*-*-*-*-*-*-*-*Set value for one contour level*-*-*-*-*-*-*-*-*-*-*-*
===============================
Double_t GetMaximum(Double_t maxval) const
Return maximum value smaller than maxval of bins in the range*-*-*-*-*-*
Int_t GetMaximumBin() const
-*-*-*-*-*Return location of bin with maximum value in the range*-*
======================================================
Int_t GetMaximumBin(Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
-*-*-*-*-*Return location of bin with maximum value in the range*-*
======================================================
Double_t GetMinimum(Double_t minval) const
Return minimum value greater than minval of bins in the range
Int_t GetMinimumBin() const
-*-*-*-*-*Return location of bin with minimum value in the range*-*
======================================================
Int_t GetMinimumBin(Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
-*-*-*-*-*Return location of bin with minimum value in the range*-*
======================================================
void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax)
-*-*-*-*-*-*-*Redefine x axis parameters*-*-*-*-*-*-*-*-*-*-*-*
===========================
The X axis parameters are modified.
The bins content array is resized
if errors (Sumw2) the errors array is resized
The previous bin contents are lost
To change only the axis limits, see TAxis::SetRange
void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax)
-*-*-*-*-*-*-*Redefine x and y axis parameters*-*-*-*-*-*-*-*-*-*-*-*
=================================
The X and Y axis parameters are modified.
The bins content array is resized
if errors (Sumw2) the errors array is resized
The previous bin contents are lost
To change only the axis limits, see TAxis::SetRange
void SetBins(Int_t nx, Axis_t xmin, Axis_t xmax, Int_t ny, Axis_t ymin, Axis_t ymax, Int_t nz, Axis_t zmin, Axis_t zmax)
-*-*-*-*-*-*-*Redefine x, y and z axis parameters*-*-*-*-*-*-*-*-*-*-*-*
====================================
The X, Y and Z axis parameters are modified.
The bins content array is resized
if errors (Sumw2) the errors array is resized
The previous bin contents are lost
To change only the axis limits, see TAxis::SetRange
void SetMaximum(Double_t maximum)
-*-*-*-*-*-*-*Set the maximum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
====================================
By default the maximum value is automatically set to the maximum
bin content plus a margin of 10 per cent.
Use TH1::GetMaximum to find the maximum value of an histogram
Use TH1::GetMaximumBin to find the bin with the maximum value of an histogram
void SetMinimum(Double_t minimum)
-*-*-*-*-*-*-*Set the minimum value for the Y axis*-*-*-*-*-*-*-*-*-*-*-*
====================================
By default the minimum value is automatically set to zero if all bin contents
are positive or the minimum - 10 per cent otherwise.
Use TH1::GetMinimum to find the minimum value of an histogram
Use TH1::GetMinimumBin to find the bin with the minimum value of an histogram
void SetDirectory(TDirectory *dir)
By default when an histogram is created, it is added to the list
of histogram objects in the current directory in memory.
Remove reference to this histogram from current directory and add
reference to new directory dir. dir can be 0 in which case the
histogram does not belong to any directory.
void SetError(const Stat_t *error)
-*-*-*-*-*-*-*Replace bin errors by values in array error*-*-*-*-*-*-*-*-*
===========================================
void SetName(const char *name)
Change the name of this histogram
void SetNameTitle(const char *name, const char *title)
Change the name and title of this histogram
void SetStats(Bool_t stats)
-*-*-*-*-*-*-*Set statistics option on/off
============================
By default, the statistics box is drawn.
The paint options can be selected via gStyle->SetOptStats.
This function sets/resets the kNoStats bin in the histogram object.
It has priority over the Style option.
void Sumw2()
-*-*-*Create structure to store sum of squares of weights*-*-*-*-*-*-*-*
===================================================
if histogram is already filled, the sum of squares of weights
is filled with the existing bin contents
The error per bin will be computed as sqrt(sum of squares of weight)
for each bin.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1* GetFunction(const char *name) const
-*-*-*Return pointer to function with name*-*-*-*-*-*-*-*-*-*-*-*-*
===================================
Functions such as TH1::Fit store the fitted function in the list of
functions of this histogram.
Stat_t GetBinError(Int_t bin) const
-*-*-*-*-*Return value of error associated to bin number bin*-*-*-*-*
==================================================
if the sum of squares of weights has been defined (via Sumw2),
this function returns the sqrt(sum of w2).
otherwise it returns the sqrt(contents) for this bin.
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Stat_t GetBinError(Int_t binx, Int_t biny) const
-*-*-*-*-*Return error of bin number binx, biny
=====================================
NB: Function to be called for 2-d histograms only
Stat_t GetBinError(Int_t binx, Int_t biny, Int_t binz) const
-*-*-*-*-*Return error of bin number binx,biny,binz
=========================================
NB: Function to be called for 3-d histograms only
Stat_t GetCellContent(Int_t binx, Int_t biny) const
-*-*-*-*-*Return content of bin number binx, biny
=====================================
NB: Function to be called for 2-d histograms only
Stat_t GetCellError(Int_t binx, Int_t biny) const
-*-*-*-*-*Return error of bin number binx, biny
=====================================
NB: Function to be called for 2-d histograms only
void SetBinError(Int_t bin, Stat_t error)
see convention for numbering bins in TH1::GetBin
void SetBinContent(Int_t binx, Int_t biny, Stat_t content)
see convention for numbering bins in TH1::GetBin
void SetBinContent(Int_t binx, Int_t biny, Int_t binz, Stat_t content)
see convention for numbering bins in TH1::GetBin
void SetCellContent(Int_t binx, Int_t biny, Stat_t content)
void SetBinError(Int_t binx, Int_t biny, Stat_t error)
see convention for numbering bins in TH1::GetBin
void SetBinError(Int_t binx, Int_t biny, Int_t binz, Stat_t error)
see convention for numbering bins in TH1::GetBin
void SetCellError(Int_t binx, Int_t biny, Stat_t error)
see convention for numbering bins in TH1::GetBin
void SetBinContent(Int_t, Stat_t)
see convention for numbering bins in TH1::GetBin
Inline Functions
Int_t AxisChoice(Option_t* axis) const
void FillN(Int_t, const Axis_t*, const Axis_t*, const Double_t*, Int_t)
Int_t GetBufferLength() const
Int_t GetBufferSize() const
const Double_t* GetBuffer() const
Double_t* GetIntegral()
TList* GetListOfFunctions() const
Int_t GetNdivisions(Option_t* axis = "X") const
Color_t GetAxisColor(Option_t* axis = "X") const
Color_t GetLabelColor(Option_t* axis = "X") const
Style_t GetLabelFont(Option_t* axis = "X") const
Float_t GetLabelOffset(Option_t* axis = "X") const
Float_t GetLabelSize(Option_t* axis = "X") const
Float_t GetTitleOffset(Option_t* axis = "X") const
Float_t GetTitleSize(Option_t* axis = "X") const
Float_t GetTickLength(Option_t* axis = "X") const
Float_t GetBarOffset() const
Float_t GetBarWidth() const
Axis_t GetBinCenter(Int_t bin) const
Axis_t GetBinLowEdge(Int_t bin) const
Axis_t GetBinWidth(Int_t bin) const
void GetCenter(Axis_t* center) const
TDirectory* GetDirectory() const
Int_t GetDimension() const
void GetLowEdge(Axis_t* edge) const
Double_t GetMaximumStored() const
Double_t GetMinimumStored() const
Int_t GetNbinsX() const
Int_t GetNbinsY() const
Int_t GetNbinsZ() const
Double_t GetNormFactor() const
Option_t* GetOption() const
Int_t GetSumw2N() const
Stat_t Integral(Int_t, Int_t, Int_t, Int_t, Option_t*) const
Stat_t Integral(Int_t, Int_t, Int_t, Int_t, Int_t, Int_t, Option_t*) const
void SetAxisColor(Color_t color = 1, Option_t* axis = "X")
void SetAxisRange(Axis_t xmin, Axis_t xmax, Option_t* axis = "X")
void SetBarOffset(Float_t offset = 0.25)
void SetBarWidth(Float_t width = 0.5)
void SetBinsLength(Int_t = -1)
void SetEntries(Stat_t n)
void SetLabelColor(Color_t color = 1, Option_t* axis = "X")
void SetLabelFont(Style_t font = 62, Option_t* axis = "X")
void SetLabelOffset(Float_t offset = 0.005, Option_t* axis = "X")
void SetLabelSize(Float_t size = 0.02, Option_t* axis = "X")
void SetNdivisions(Int_t n = 510, Option_t* axis = "X")
void SetNormFactor(Double_t factor = 1)
void SetOption(Option_t* option = " ")
void SetTickLength(Float_t length = 0.02, Option_t* axis = "X")
void SetTitleOffset(Float_t offset = 1, Option_t* axis = "X")
void SetTitleSize(Float_t size = 0.02, Option_t* axis = "X")
void SetXTitle(const char* title)
void SetYTitle(const char* title)
void SetZTitle(const char* title)
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void StreamerNVirtual(TBuffer& b)
TH1& operator=(const TH1&)
Author: Rene Brun 26/12/94
Last update: root/hist:$Name: $:$Id: TH1.cxx,v 1.211 2004/11/26 15:07:49 brun Exp $
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
*/