| #include "TMultiLayerPerceptron.h" |
| Inheritance Chart: | |||||||||
|
private:
void BuildFirstLayer(TString&)
void BuildHiddenLayers(TString&)
void BuildLastLayer(TString&, Int_t)
void MLP_Line(Double_t*, Double_t*, Double_t)
void Shuffle(Int_t*, Int_t) const
protected:
void AttachData()
void BFGSDir(TMatrixD&, Double_t*)
void BuildNetwork()
void ConjugateGradientsDir(Double_t*, Double_t)
Double_t DerivDir(Double_t*)
bool GetBFGSH(TMatrixD&, TMatrixD&, TMatrixD&)
void GetEntry(Int_t) const
Bool_t LineSearch(Double_t*, Double_t*)
void MLP_Batch(Double_t*)
void MLP_Stochastic(Double_t*)
void SetGammaDelta(TMatrixD&, TMatrixD&, Double_t*)
void SteepestDir(Double_t*)
public:
TMultiLayerPerceptron()
TMultiLayerPerceptron(const char* layout, TTree* data = NULL, const char* training = "Entry$%2==0", const char* test)
TMultiLayerPerceptron(const char* layout, const char* weight, TTree* data = NULL, const char* training = "Entry$%2==0", const char* test)
TMultiLayerPerceptron(const char* layout, TTree* data, TEventList* training, TEventList* test)
TMultiLayerPerceptron(const char* layout, const char* weight, TTree* data, TEventList* training, TEventList* test)
virtual ~TMultiLayerPerceptron()
static TClass* Class()
void ComputeDEDw() const
virtual void Draw(Option_t* option)
void DrawResult(Int_t index = 0, Option_t* option) const
void DumpWeights(Option_t* filename) const
Double_t Evaluate(Int_t index, Double_t* params) const
void Export(Option_t* filename = "NNfunction", Option_t* language = "C++") const
Double_t GetDelta() const
Double_t GetEpsilon() const
Double_t GetError(Int_t event) const
Double_t GetError(TMultiLayerPerceptron::DataSet set) const
Double_t GetEta() const
Double_t GetEtaDecay() const
Int_t GetReset() const
TString GetStructure() const
Double_t GetTau() const
virtual TClass* IsA() const
void LoadWeights(Option_t* filename)
void Randomize() const
Double_t Result(Int_t event, Int_t index = 0) const
void SetData(TTree*)
void SetDelta(Double_t delta)
void SetEpsilon(Double_t eps)
void SetEta(Double_t eta)
void SetEtaDecay(Double_t ed)
void SetEventWeight(const char*)
void SetLearningMethod(TMultiLayerPerceptron::LearningMethod method)
void SetReset(Int_t reset)
void SetTau(Double_t tau)
void SetTestDataSet(TEventList* test)
void SetTestDataSet(const char* test)
void SetTrainingDataSet(TEventList* train)
void SetTrainingDataSet(const char* train)
virtual void ShowMembers(TMemberInspector& insp, char* parent)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
void Train(Int_t nEpoch, Option_t* option = "text")
private:
TTree* fData ! pointer to the tree used as datasource
Int_t fCurrentTree ! index of the current tree in a chain
Double_t fCurrentTreeWeight ! weight of the current tree in a chain
TObjArray fNetwork Collection of all the neurons in the network
TObjArray fFirstLayer Collection of the input neurons; subset of fNetwork
TObjArray fLastLayer Collection of the output neurons; subset of fNetwork
TObjArray fSynapses Collection of all the synapses in the network
TString fStructure String containing the network structure
TString fWeight String containing the event weight
TEventList* fTraining ! EventList defining the events in the training dataset
TEventList* fTest ! EventList defining the events in the test dataset
TMultiLayerPerceptron::LearningMethod fLearningMethod ! The Learning Method
TTreeFormula* fEventWeight ! formula representing the event weight
TTreeFormulaManager* fManager ! TTreeFormulaManager for the weight and neurons
Double_t fEta ! Eta - used in stochastic minimisation - Default=0.1
Double_t fEpsilon ! Epsilon - used in stochastic minimisation - Default=0.
Double_t fDelta ! Delta - used in stochastic minimisation - Default=0.
Double_t fEtaDecay ! EtaDecay - Eta *= EtaDecay at each epoch - Default=1.
Double_t fTau ! Tau - used in line search - Default=3.
Double_t fLastAlpha ! internal parameter used in line search
Int_t fReset ! number of epochs between two resets of the search direction to the steepest descent - Default=50
Bool_t fTrainingOwner ! internal flag whether one has to delete fTraining or not
Bool_t fTestOwner ! internal flag whether one has to delete fTest or not
public:
static const TMultiLayerPerceptron::LearningMethod kStochastic
static const TMultiLayerPerceptron::LearningMethod kBatch
static const TMultiLayerPerceptron::LearningMethod kSteepestDescent
static const TMultiLayerPerceptron::LearningMethod kRibierePolak
static const TMultiLayerPerceptron::LearningMethod kFletcherReeves
static const TMultiLayerPerceptron::LearningMethod kBFGS
static const TMultiLayerPerceptron::DataSet kTraining
static const TMultiLayerPerceptron::DataSet kTest
TMultiLayerPerceptron This class describes a neural network. There are facilities to train the network and use the output. The input layer is made of inactive neurons (returning the normalized input), hidden layers are made of sigmoids and output neurons are linear. The basic input is a TTree and two (training and test) TEventLists. Input and output neurons are assigned a value computed for each event with the same possibilities as for TTree::Draw(). Events may be weighted individualy or via TTree::SetWeight(). 6 learning methods are available: kStochastic, kBatch, kSteepestDescent, kRibierePolak, kFletcherReeves and kBFGS. This implementation, written by C. Delaere, is *inspired* from the mlpfit package from J.Schwindling et al.
Neural Networks are more and more used in various fields for data analysis and classification, both for research and commercial institutions. Some randomly choosen examples are:
image analysis
financial movements predictions and analysis
sales forecast and product shipping optimisation
in particles physics: mainly for classification tasks (signal over background discrimination)
More than 50% of neural networks are multilayer perceptrons. This implementation of multilayer perceptrons is inspired from the MLPfit package originaly written by Jerome Schwindling. MLPfit remains one of the fastest tool for neural networks studies, and this ROOT add-on will not try to compete on that. A clear and flexible Object Oriented implementation has been choosen over a faster but more difficult to maintain code. Nevertheless, the time penalty does not exceed a factor 2.
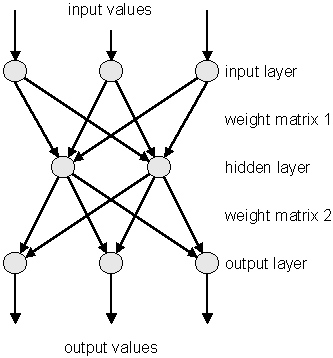
The multilayer perceptron is a simple feed-forward network with the following structure:

It is made of neurons characterized by a bias and weighted links between them (let's call those links synapses). The input neurons receive the inputs, normalize them and forward them to the first hidden layer.
Each neuron in any subsequent layer first computes a linear combination of the outputs of the previous layer. The output of the neuron is then function of that combination with f being linear for output neurons or a sigmoid for hidden layers. This is useful because of two theorems:
A linear combination of sigmoids can approximate any continuous function.
Trained with output = 1 for the signal and 0 for the background, the approximated function of inputs X is the probability of signal, knowing X.
The aim of all learning methods is to minimize the total error on a set of weighted examples. The error is defined as the sum in quadrature, devided by two, of the error on each individual output neuron.
In all methods implemented, one needs to compute the first derivative of that error with respect to the weights. Exploiting the well-known properties of the derivative, especialy the derivative of compound functions, one can write:
for a neuton: product of the local derivative with the weighted sum on the outputs of the derivatives.
for a synapse: product of the input with the local derivative of the output neuron.
This computation is called back-propagation of the errors. A loop over all examples is called an epoch.
Six learning methods are implemented.
Stochastic minimization: This is the most trivial learning method. This is the Robbins-Monro stochastic approximation applied to multilayer perceptrons. The weights are updated after each example according to the formula:
$w_{ij}(t+1) = w_{ij}(t) + \Delta w_{ij}(t)$
with
$\Delta w_{ij}(t) = - \eta(\d e_p / \d w_{ij} + \delta) + \epsilon \Deltaw_{ij}(t-1)$
The parameters for this method are Eta, EtaDecay, Delta and Epsilon.
Steepest descent with fixed step size (batch learning): It is the same as the stochastic minimization, but the weights are updated after considering all the examples, with the total derivative dEdw. The parameters for this method are Eta, EtaDecay, Delta and Epsilon.
Steepest descent algorithm: Weights are set to the minimum along the line defined by the gradient. The only parameter for this method is Tau. Lower tau = higher precision = slower search. A value Tau = 3 seems reasonable.
Conjugate gradients with the Polak-Ribiere updating formula: Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepes descent.
Conjugate gradients with the Fletcher-Reeves updating formula: Weights are set to the minimum along the line defined by the conjugate gradient. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepes descent.
Broyden, Fletcher, Goldfarb, Shanno (BFGS) method: Implies the computation of a NxN matrix computation, but seems more powerful at least for less than 300 weights. Parameters are Tau and Reset, which defines the epochs where the direction is reset to the steepes descent.
TMLP is build from 3 classes: TNeuron, TSynapse and TMultiLayerPerceptron. Only TMultiLayerPerceptron should be used explicitely by the user.
TMultiLayerPerceptron will take examples from a TTree given in the constructor. The network is described by a simple string: The input/output layers are defined by giving the expression for each neuron, separated by comas. Hidden layers are just described by the number of neurons. The layers are separated by semicolons. In addition, output layer formulas can be preceded by '@' (e.g "@out") if one wants to also normalize the output. Input and outputs are taken from the TTree given as second argument. Expressions are evaluated as for TTree::Draw(). One defines the training and test datasets by TEventLists.
Example: TMultiLayerPerceptron("x,y:10:5:f",inputTree);
Both the TTree and the TEventLists can be defined in the constructor, or later with the suited setter method.
The learning method is defined using the TMultiLayerPerceptron::SetLearningMethod() . Learning methods are :
TMultiLayerPerceptron::kStochastic,
TMultiLayerPerceptron::kBatch,
TMultiLayerPerceptron::kSteepestDescent,
TMultiLayerPerceptron::kRibierePolak,
TMultiLayerPerceptron::kFletcherReeves,
TMultiLayerPerceptron::kBFGS
A weight can be assigned to events, either in the constructor, either with TMultiLayerPerceptron::SetEventWeight(). In addition, the TTree weight is taken into account.
Finally, one starts the training with
TMultiLayerPerceptron::Train(Int_t nepoch, Option_t* options). The
output neurons can be normalized, this is not the case for mlpfit the neural net is exported in C++ (not in FORTRAN) the drawResult() method allows a fast check of the learning procedure
TMultiLayerPerceptron()
Default constructor
TMultiLayerPerceptron(const char * layout, TTree * data,
TEventList * training,
TEventList * test)
The network is described by a simple string:
The input/output layers are defined by giving
the branch names separated by comas.
Hidden layers are just described by the number of neurons.
The layers are separated by semicolons.
Ex: "x,y:10:5:f"
The output can be prepended by '@' if the variable has to be
normalized.
Input and outputs are taken from the TTree given as second argument.
training and test are the two TEventLists defining events
to be used during the neural net training.
Both the TTree and the TEventLists can be defined in the constructor,
or later with the suited setter method.
TMultiLayerPerceptron(const char * layout, const char * weight, TTree * data,
TEventList * training,
TEventList * test)
The network is described by a simple string:
The input/output layers are defined by giving
the branch names separated by comas.
Hidden layers are just described by the number of neurons.
The layers are separated by semicolons.
Ex: "x,y:10:5:f"
The output can be prepended by '@' if the variable has to be
normalized.
Input and outputs are taken from the TTree given as second argument.
training and test are the two TEventLists defining events
to be used during the neural net training.
Both the TTree and the TEventLists can be defined in the constructor,
or later with the suited setter method.
TMultiLayerPerceptron(const char * layout, TTree * data,
const char * training,
const char * test)
The network is described by a simple string:
The input/output layers are defined by giving
the branch names separated by comas.
Hidden layers are just described by the number of neurons.
The layers are separated by semicolons.
Ex: "x,y:10:5:f"
The output can be prepended by '@' if the variable has to be
normalized.
Input and outputs are taken from the TTree given as second argument.
training and test are two cuts (see TTreeFormula) defining events
to be used during the neural net training and testing.
Example: "Entry$%2", "(Entry$+1)%2".
Both the TTree and the cut can be defined in the constructor,
or later with the suited setter method.
TMultiLayerPerceptron(const char * layout, const char * weight, TTree * data,
const char * training,
const char * test)
The network is described by a simple string:
The input/output layers are defined by giving
the branch names separated by comas.
Hidden layers are just described by the number of neurons.
The layers are separated by semicolons.
Ex: "x,y:10:5:f"
The output can be prepended by '@' if the variable has to be
normalized.
Input and outputs are taken from the TTree given as second argument.
training and test are two cuts (see TTreeFormula) defining events
to be used during the neural net training and testing.
Example: "Entry$%2", "(Entry$+1)%2".
Both the TTree and the cut can be defined in the constructor,
or later with the suited setter method.
~TMultiLayerPerceptron()
void SetData(TTree * data)
Set the data source
void SetEventWeight(const char * branch)
Set the event weight
void SetTrainingDataSet(TEventList* train)
Sets the Training dataset.
Those events will be used for the minimization
void SetTestDataSet(TEventList* test)
Sets the Test dataset.
Those events will not be used for the minimization but for control
void SetTrainingDataSet(const char * train)
Sets the Training dataset.
Those events will be used for the minimization.
Note that the tree must be already defined.
void SetTestDataSet(const char * test)
Sets the Test dataset.
Those events will not be used for the minimization but for control.
Note that the tree must be already defined.
void SetLearningMethod(TMultiLayerPerceptron::LearningMethod method)
Sets the learning method.
Available methods are: kStochastic, kBatch,
kSteepestDescent, kRibierePolak, kFletcherReeves and kBFGS.
(look at the constructor for the complete description
of learning methods and parameters)
void SetEta(Double_t eta)
Sets Eta - used in stochastic minimisation
(look at the constructor for the complete description
of learning methods and parameters)
void SetEpsilon(Double_t eps)
Sets Epsilon - used in stochastic minimisation
(look at the constructor for the complete description
of learning methods and parameters)
void SetDelta(Double_t delta)
Sets Delta - used in stochastic minimisation
(look at the constructor for the complete description
of learning methods and parameters)
void SetEtaDecay(Double_t ed)
Sets EtaDecay - Eta *= EtaDecay at each epoch
(look at the constructor for the complete description
of learning methods and parameters)
void SetTau(Double_t tau)
Sets Tau - used in line search
(look at the constructor for the complete description
of learning methods and parameters)
void SetReset(Int_t reset)
Sets number of epochs between two resets of the
search direction to the steepest descent.
(look at the constructor for the complete description
of learning methods and parameters)
void GetEntry(Int_t entry) const
Load an entry into the network
void Train(Int_t nEpoch, Option_t * option)
Train the network.
nEpoch is the number of iterations.
option can contain:
- "text" (simple text output)
- "graph" (evoluting graphical training curves)
- "update=X" (step for the text/graph output update)
- "+" will skip the randomisation and start from the previous values.
All combinations are available.
Double_t Result(Int_t event, Int_t index) const
Computes the output for a given event.
Look at the output neuron designed by index.
Double_t GetError(Int_t event) const
Error on the output for a given event
Double_t GetError(TMultiLayerPerceptron::DataSet set) const
Error on the whole dataset
void ComputeDEDw() const
Compute the DEDw = sum on all training events of dedw for each weight
normalized by the number of events.
void Randomize() const
Randomize the weights
void AttachData()
Connects the TTree to Neurons in input and output
layers. The formulas associated to each neuron are created
and reported to the network formula manager.
By default, the branch is not normalised since this would degrade
performance for classification jobs.
Normalisation can be requested by putting '@' in front of the formula.
void BuildNetwork()
Instanciates the network from the description
void BuildFirstLayer(TString & input)
Instanciates the neurons in input
Inputs are normalised and the type is set to kOff
(simple forward of the formula value)
void BuildHiddenLayers(TString & hidden)
Builds hidden layers.
Neurons are Sigmoids.
void BuildLastLayer(TString & output, Int_t prev)
Builds the output layer
Neurons are linear combinations of input.
void DrawResult(Int_t index, Option_t * option) const
Draws the neural net output
It produces an histogram with the output for the two datasets.
Index is the number of the desired output neuron.
"option" can contain:
- test or train to select a dataset
- comp to produce a X-Y comparison plot
- nocanv to not create a new TCanvas for the plot
void DumpWeights(Option_t * filename) const
Dumps the weights to a text file.
Set filename to "-" (default) to dump to the standard output
void LoadWeights(Option_t * filename)
Loads the weights from a text file conforming to the format
defined by DumpWeights.
Double_t Evaluate(Int_t index, Double_t *params) const
Returns the Neural Net for a given set of input parameters
#parameters must equal #input neurons
void Export(Option_t * filename, Option_t * language) const
Exports the NN as a function for any non-ROOT-dependant code
Supported languages are: only C++ , FORTRAN and Python (yet)
This feature is also usefull if you want to plot the NN as
a function (TF1 or TF2).
void Shuffle(Int_t * index, Int_t n) const
Shuffle the Int_t index[n] in input.
Input:
index: the array to shuffle
n: the size of the array
Output:
index: the shuffled indexes
This method is used for stochastic training
void MLP_Stochastic(Double_t * buffer)
One step for the stochastic method
buffer should contain the previous dw vector and will be updated
void MLP_Batch(Double_t * buffer)
One step for the batch (stochastic) method.
DEDw should have been updated before calling this.
void MLP_Line(Double_t * origin, Double_t * dir, Double_t dist)
Sets the weights to a point along a line
Weights are set to [origin + (dist * dir)].
void SteepestDir(Double_t * dir)
Sets the search direction to steepest descent.
bool LineSearch(Double_t * direction, Double_t * buffer)
Search along the line defined by direction.
buffer is not used but is updated with the new dw
so that it can be used by a later stochastic step.
It returns true if the line search fails.
void ConjugateGradientsDir(Double_t * dir, Double_t beta)
Sets the search direction to conjugate gradient direction
beta should be:
||g_{(t+1)}||^2 / ||g_{(t)}||^2 (Fletcher-Reeves)
g_{(t+1)} (g_{(t+1)}-g_{(t)}) / ||g_{(t)}||^2 (Ribiere-Polak)
bool GetBFGSH(TMatrixD & BFGSH, TMatrixD & gamma, TMatrixD & delta)
Computes the hessian matrix using the BFGS update algorithm.
from gamma (g_{(t+1)}-g_{(t)}) and delta (w_{(t+1)}-w_{(t)}).
It returns true if such a direction could not be found
(if gamma and delta are orthogonal).
void SetGammaDelta(TMatrixD & gamma, TMatrixD & delta,
Double_t * buffer)
Sets the gamma (g_{(t+1)}-g_{(t)}) and delta (w_{(t+1)}-w_{(t)}) vectors
Gamma is computed here, so ComputeDEDw cannot have been called before,
and delta is a direct translation of buffer into a TMatrixD.
Double_t DerivDir(Double_t * dir)
scalar product between gradient and direction
= derivative along direction
void BFGSDir(TMatrixD & BFGSH, Double_t * dir)
Computes the direction for the BFGS algorithm as the product
between the Hessian estimate (BFGSH) and the dir.
void Draw(Option_t * /*option*/)
Draws the network structure.
Neurons are depicted by a blue disk, and synapses by
lines connecting neurons.
The line width is proportionnal to the weight.
Inline Functions
Double_t GetEta() const
Double_t GetEpsilon() const
Double_t GetDelta() const
Double_t GetEtaDecay() const
Double_t GetTau() const
Int_t GetReset() const
TString GetStructure() const
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
Author: Christophe.Delaere@cern.ch 20/07/03
Last update: root/mlp:$Name: $:$Id: TMultiLayerPerceptron.cxx,v 1.24 2004/12/16 21:20:47 brun Exp $
Copyright (C) 1995-2003, Rene Brun and Fons Rademakers. *