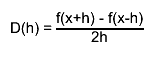| TF1() |
| TF1(const TF1& f1) |
| TF1(const char* name, const char* formula, Double_t xmin = 0, Double_t xmax = 1) |
| TF1(const char* name, Double_t xmin, Double_t xmax, Int_t npar) |
| TF1(const char* name, void* fcn, Double_t xmin, Double_t xmax, Int_t npar) |
| TF1(const char* name, ROOT::Math::ParamFunctor f, Double_t xmin = 0, Double_t xmax = 1, Int_t npar = 0) |
| TF1(const char* name, void* ptr, Double_t xmin, Double_t xmax, Int_t npar, char* className) |
| TF1(const char* name, void* ptr, void*, Double_t xmin, Double_t xmax, Int_t npar, char* className, char* methodName = 0) |
| virtual | ~TF1() |
| void | TObject::AbstractMethod(const char* method) const |
| static void | AbsValue(Bool_t reject = kTRUE) |
| virtual void | TFormula::Analyze(const char* schain, Int_t& err, Int_t offset = 0) |
| virtual Bool_t | TFormula::AnalyzeFunction(TString& chaine, Int_t& err, Int_t offset = 0) |
| virtual void | TObject::AppendPad(Option_t* option = "") |
| virtual void | Browse(TBrowser* b) |
| static void | CalcGaussLegendreSamplingPoints(Int_t num, Double_t* x, Double_t* w, Double_t eps = 3.0e-11) |
| virtual Double_t | CentralMoment(Double_t n, Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001) |
| static TClass* | Class() |
| virtual const char* | TObject::ClassName() const |
| virtual void | TFormula::Clear(Option_t* option = "") |
| virtual TObject* | TNamed::Clone(const char* newname = "") const |
| virtual Int_t | TNamed::Compare(const TObject* obj) const |
| virtual Int_t | TFormula::Compile(const char* expression = "") |
| virtual void | Copy(TObject& f1) const |
| virtual char* | TFormula::DefinedString(Int_t code) |
| virtual Double_t | TFormula::DefinedValue(Int_t code) |
| virtual Int_t | TFormula::DefinedVariable(TString& variable, Int_t& action) |
| virtual void | TObject::Delete(Option_t* option = "")MENU |
| virtual Double_t | Derivative(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const |
| virtual Double_t | Derivative2(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const |
| virtual Double_t | Derivative3(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const |
| static Double_t | DerivativeError() |
| Int_t | TAttLine::DistancetoLine(Int_t px, Int_t py, Double_t xp1, Double_t yp1, Double_t xp2, Double_t yp2) |
| virtual Int_t | DistancetoPrimitive(Int_t px, Int_t py) |
| virtual void | Draw(Option_t* option = "") |
| virtual void | TObject::DrawClass() constMENU |
| virtual TObject* | TObject::DrawClone(Option_t* option = "") constMENU |
| virtual TF1* | DrawCopy(Option_t* option = "") const |
| virtual void | DrawDerivative(Option_t* option = "al")MENU |
| virtual void | DrawF1(const char* formula, Double_t xmin, Double_t xmax, Option_t* option = "") |
| virtual void | DrawIntegral(Option_t* option = "al")MENU |
| virtual void | TObject::Dump() constMENU |
| virtual void | TObject::Error(const char* method, const char* msgfmt) const |
| virtual Double_t | Eval(Double_t x, Double_t y = 0, Double_t z = 0, Double_t t = 0) const |
| virtual Double_t | EvalPar(const Double_t* x, const Double_t* params = 0) |
| virtual Double_t | TFormula::EvalParOld(const Double_t* x, const Double_t* params = 0) |
| virtual void | TObject::Execute(const char* method, const char* params, Int_t* error = 0) |
| virtual void | TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0) |
| virtual void | ExecuteEvent(Int_t event, Int_t px, Int_t py) |
| virtual void | TObject::Fatal(const char* method, const char* msgfmt) const |
| virtual void | TNamed::FillBuffer(char*& buffer) |
| virtual TObject* | TObject::FindObject(const char* name) const |
| virtual TObject* | TObject::FindObject(const TObject* obj) const |
| virtual void | FixParameter(Int_t ipar, Double_t value) |
| Double_t | GetChisquare() const |
| static TF1* | GetCurrent() |
| virtual Option_t* | TObject::GetDrawOption() const |
| static Long_t | TObject::GetDtorOnly() |
| virtual TString | TFormula::GetExpFormula(Option_t* option = "") const |
| virtual Color_t | TAttFill::GetFillColor() const |
| virtual Style_t | TAttFill::GetFillStyle() const |
| TH1* | GetHistogram() const |
| virtual const char* | TObject::GetIconName() const |
| virtual const TObject* | TFormula::GetLinearPart(Int_t i) |
| virtual Color_t | TAttLine::GetLineColor() const |
| virtual Style_t | TAttLine::GetLineStyle() const |
| virtual Width_t | TAttLine::GetLineWidth() const |
| virtual Color_t | TAttMarker::GetMarkerColor() const |
| virtual Size_t | TAttMarker::GetMarkerSize() const |
| virtual Style_t | TAttMarker::GetMarkerStyle() const |
| virtual Double_t | GetMaximum(Double_t xmin = 0, Double_t xmax = 0) const |
| virtual Double_t | GetMaximumX(Double_t xmin = 0, Double_t xmax = 0) const |
| TMethodCall* | GetMethodCall() const |
| virtual Double_t | GetMinimum(Double_t xmin = 0, Double_t xmax = 0) const |
| virtual Double_t | GetMinimumX(Double_t xmin = 0, Double_t xmax = 0) const |
| virtual const char* | TNamed::GetName() const |
| virtual Int_t | GetNDF() const |
| virtual Int_t | TFormula::GetNdim() const |
| virtual Int_t | TFormula::GetNpar() const |
| virtual Int_t | GetNpx() const |
| virtual Int_t | TFormula::GetNumber() const |
| virtual Int_t | GetNumberFitPoints() const |
| virtual Int_t | GetNumberFreeParameters() const |
| virtual char* | GetObjectInfo(Int_t px, Int_t py) const |
| static Bool_t | TObject::GetObjectStat() |
| virtual Option_t* | TObject::GetOption() const |
| Double_t | TFormula::GetParameter(Int_t ipar) const |
| Double_t | TFormula::GetParameter(const char* name) const |
| virtual Double_t* | TFormula::GetParameters() const |
| virtual void | TFormula::GetParameters(Double_t* params) |
| TObject* | GetParent() const |
| virtual Double_t | GetParError(Int_t ipar) const |
| virtual Double_t* | GetParErrors() const |
| virtual void | GetParLimits(Int_t ipar, Double_t& parmin, Double_t& parmax) const |
| virtual const char* | TFormula::GetParName(Int_t ipar) const |
| virtual Int_t | TFormula::GetParNumber(const char* name) const |
| virtual Double_t | GetProb() const |
| virtual Int_t | GetQuantiles(Int_t nprobSum, Double_t* q, const Double_t* probSum) |
| virtual Double_t | GetRandom() |
| virtual Double_t | GetRandom(Double_t xmin, Double_t xmax) |
| virtual void | GetRange(Double_t& xmin, Double_t& xmax) const |
| virtual void | GetRange(Double_t& xmin, Double_t& ymin, Double_t& xmax, Double_t& ymax) const |
| virtual void | GetRange(Double_t& xmin, Double_t& ymin, Double_t& zmin, Double_t& xmax, Double_t& ymax, Double_t& zmax) const |
| virtual Double_t | GetSave(const Double_t* x) |
| virtual const char* | TNamed::GetTitle() const |
| virtual UInt_t | TObject::GetUniqueID() const |
| virtual Double_t | GetX(Double_t y, Double_t xmin = 0, Double_t xmax = 0) const |
| TAxis* | GetXaxis() const |
| virtual Double_t | GetXmax() const |
| virtual Double_t | GetXmin() const |
| TAxis* | GetYaxis() const |
| TAxis* | GetZaxis() const |
| virtual Double_t | GradientPar(Int_t ipar, const Double_t* x, Double_t eps = 0.01) |
| virtual void | GradientPar(const Double_t* x, Double_t* grad, Double_t eps = 0.01) |
| virtual Bool_t | TObject::HandleTimer(TTimer* timer) |
| virtual ULong_t | TNamed::Hash() const |
| virtual void | TObject::Info(const char* method, const char* msgfmt) const |
| virtual Bool_t | TObject::InheritsFrom(const char* classname) const |
| virtual Bool_t | TObject::InheritsFrom(const TClass* cl) const |
| virtual void | InitArgs(const Double_t* x, const Double_t* params) |
| static void | InitStandardFunctions() |
| virtual void | TObject::Inspect() constMENU |
| virtual Double_t | Integral(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 1e-12) |
| virtual Double_t | Integral(Double_t ax, Double_t bx, Double_t ay, Double_t by, Double_t epsilon = 1e-12) |
| virtual Double_t | Integral(Double_t ax, Double_t bx, Double_t ay, Double_t by, Double_t az, Double_t bz, Double_t epsilon = 1e-12) |
| virtual Double_t | IntegralError(Double_t a, Double_t b, Double_t epsilon = 1e-12) |
| virtual Double_t | IntegralFast(Int_t num, Double_t* x, Double_t* w, Double_t a, Double_t b, Double_t* params = 0, Double_t epsilon = 1e-12) |
| virtual Double_t | IntegralMultiple(Int_t n, const Double_t* a, const Double_t* b, Double_t epsilon, Double_t& relerr) |
| virtual Double_t | IntegralMultiple(Int_t n, const Double_t* a, const Double_t* b, Int_t minpts, Int_t maxpts, Double_t epsilon, Double_t& relerr, Int_t& nfnevl, Int_t& ifail) |
| void | TObject::InvertBit(UInt_t f) |
| virtual TClass* | IsA() const |
| virtual Bool_t | TObject::IsEqual(const TObject* obj) const |
| virtual Bool_t | TObject::IsFolder() const |
| virtual Bool_t | IsInside(const Double_t* x) const |
| virtual Bool_t | TFormula::IsLinear() |
| virtual Bool_t | TFormula::IsNormalized() |
| Bool_t | TObject::IsOnHeap() const |
| virtual Bool_t | TNamed::IsSortable() const |
| virtual Bool_t | TAttFill::IsTransparent() const |
| Bool_t | TObject::IsZombie() const |
| virtual void | TNamed::ls(Option_t* option = "") const |
| void | TObject::MayNotUse(const char* method) const |
| virtual Double_t | Mean(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001) |
| virtual void | TAttLine::Modify() |
| virtual Double_t | Moment(Double_t n, Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001) |
| virtual Bool_t | TObject::Notify() |
| static void | TObject::operator delete(void* ptr) |
| static void | TObject::operator delete(void* ptr, void* vp) |
| static void | TObject::operator delete[](void* ptr) |
| static void | TObject::operator delete[](void* ptr, void* vp) |
| void* | TObject::operator new(size_t sz) |
| void* | TObject::operator new(size_t sz, void* vp) |
| void* | TObject::operator new[](size_t sz) |
| void* | TObject::operator new[](size_t sz, void* vp) |
| virtual Double_t | operator()(const Double_t* x, const Double_t* params = 0) |
| virtual Double_t | operator()(Double_t x, Double_t y = 0, Double_t z = 0, Double_t t = 0) const |
| TF1& | operator=(const TF1& rhs) |
| void | TFormula::Optimize() |
| virtual void | Paint(Option_t* option = "") |
| virtual void | TObject::Pop() |
| virtual void | Print(Option_t* option = "") const |
| virtual void | TFormula::ProcessLinear(TString& replaceformula) |
| virtual Int_t | TObject::Read(const char* name) |
| virtual void | TObject::RecursiveRemove(TObject* obj) |
| static Bool_t | RejectedPoint() |
| static void | RejectPoint(Bool_t reject = kTRUE) |
| virtual void | ReleaseParameter(Int_t ipar) |
| virtual void | TAttFill::ResetAttFill(Option_t* option = "") |
| virtual void | TAttLine::ResetAttLine(Option_t* option = "") |
| virtual void | TAttMarker::ResetAttMarker(Option_t* toption = "") |
| void | TObject::ResetBit(UInt_t f) |
| virtual void | Save(Double_t xmin, Double_t xmax, Double_t ymin, Double_t ymax, Double_t zmin, Double_t zmax) |
| virtual void | TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU |
| virtual void | TAttFill::SaveFillAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1001) |
| virtual void | TAttLine::SaveLineAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1, Int_t widdef = 1) |
| virtual void | TAttMarker::SaveMarkerAttributes(ostream& out, const char* name, Int_t coldef = 1, Int_t stydef = 1, Int_t sizdef = 1) |
| virtual void | SavePrimitive(ostream& out, Option_t* option = "") |
| void | TObject::SetBit(UInt_t f) |
| void | TObject::SetBit(UInt_t f, Bool_t set) |
| virtual void | SetChisquare(Double_t chi2) |
| static void | SetCurrent(TF1* f1) |
| virtual void | TObject::SetDrawOption(Option_t* option = "")MENU |
| static void | TObject::SetDtorOnly(void* obj) |
| virtual void | TAttFill::SetFillAttributes()MENU |
| virtual void | TAttFill::SetFillColor(Color_t fcolor) |
| virtual void | TAttFill::SetFillStyle(Style_t fstyle) |
| virtual void | TAttLine::SetLineAttributes()MENU |
| virtual void | TAttLine::SetLineColor(Color_t lcolor) |
| virtual void | TAttLine::SetLineStyle(Style_t lstyle) |
| virtual void | TAttLine::SetLineWidth(Width_t lwidth) |
| virtual void | TAttMarker::SetMarkerAttributes()MENU |
| virtual void | TAttMarker::SetMarkerColor(Color_t tcolor = 1) |
| virtual void | TAttMarker::SetMarkerSize(Size_t msize = 1) |
| virtual void | TAttMarker::SetMarkerStyle(Style_t mstyle = 1) |
| static void | TFormula::SetMaxima(Int_t maxop = 1000, Int_t maxpar = 1000, Int_t maxconst = 1000) |
| virtual void | SetMaximum(Double_t maximum = -1111)MENU |
| virtual void | SetMinimum(Double_t minimum = -1111)MENU |
| virtual void | TNamed::SetName(const char* name)MENU |
| virtual void | TNamed::SetNameTitle(const char* name, const char* title) |
| virtual void | SetNDF(Int_t ndf) |
| virtual void | SetNpx(Int_t npx = 100)MENU |
| virtual void | TFormula::SetNumber(Int_t number) |
| virtual void | SetNumberFitPoints(Int_t npfits) |
| static void | TObject::SetObjectStat(Bool_t stat) |
| virtual void | TFormula::SetParameter(const char* name, Double_t parvalue) |
| virtual void | TFormula::SetParameter(Int_t ipar, Double_t parvalue) |
| virtual void | TFormula::SetParameters(const Double_t* params) |
| virtual void | TFormula::SetParameters(Double_t p0, Double_t p1, Double_t p2 = 0, Double_t p3 = 0, Double_t p4 = 0, Double_t p5 = 0, Double_t p6 = 0, Double_t p7 = 0, Double_t p8 = 0, Double_t p9 = 0, Double_t p10 = 0)MENU |
| virtual void | SetParent(TObject* p = 0) |
| virtual void | SetParError(Int_t ipar, Double_t error) |
| virtual void | SetParErrors(const Double_t* errors) |
| virtual void | SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax) |
| virtual void | TFormula::SetParName(Int_t ipar, const char* name) |
| virtual void | TFormula::SetParNames(const char* name0 = "p0", const char* name1 = "p1", const char* name2 = "p2", const char* name3 = "p3", const char* name4 = "p4", const char* name5 = "p5", const char* name6 = "p6", const char* name7 = "p7", const char* name8 = "p8", const char* name9 = "p9", const char* name10 = "p10")MENU |
| virtual void | SetRange(Double_t xmin, Double_t xmax)MENU |
| virtual void | SetRange(Double_t xmin, Double_t ymin, Double_t xmax, Double_t ymax) |
| virtual void | SetRange(Double_t xmin, Double_t ymin, Double_t zmin, Double_t xmax, Double_t ymax, Double_t zmax) |
| virtual void | SetSavedPoint(Int_t point, Double_t value) |
| virtual void | SetTitle(const char* title = "")MENU |
| virtual void | TObject::SetUniqueID(UInt_t uid) |
| virtual void | ShowMembers(TMemberInspector& insp, char* parent) |
| virtual Int_t | TNamed::Sizeof() const |
| virtual void | Streamer(TBuffer& b) |
| void | StreamerNVirtual(TBuffer& b) |
| virtual void | TObject::SysError(const char* method, const char* msgfmt) const |
| Bool_t | TObject::TestBit(UInt_t f) const |
| Int_t | TObject::TestBits(UInt_t f) const |
| virtual void | Update() |
| virtual void | TObject::UseCurrentStyle() |
| virtual Double_t | Variance(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001) |
| virtual void | TObject::Warning(const char* method, const char* msgfmt) const |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const |