
class TGraphPainter: public TVirtualGraphPainter
The graph painter class
Introduction
Graphs are drawn via the painter TGraphPainter class. This class implement all the various techniques need to display the various kind of graphs ie: TGraph, TGraphAsymmErrors, TGraphBentErrors and TGraphErrors.To draw a graph "g" is enough to do:
g->Draw("AL");
The option "AL" in the Draw() method means that the axis
syetem should be define (option "A") and that the graph should
be drawn as a simple line (option "L"). By default a graph is drawn
in the current pad in the current coordinates system. To define a suitable
coordinates system and drawn the axis the option "A" must be
specified.
TGraphPainter offers many options to paint the various kind of graphs.
The TGraphPainter class specializes in the drawing of graphs. It is separated from the graph so that one can have graphs without the graphics overhead, for example in a batch program.
When a displayed graph is modified, there is not need to call the Draw() method again; the image will be refreshed the next time the pad will be updated.
A pad is updated after one of these three actions:
- a carriage control on the ROOT command line,
- a click inside the pad,
- a call to TPad::Update.
Graphs' plotting options
Graphs can be drawn with the following options:
| "A" | Axis are drawn around the graph |
|---|---|
| "L" | A simple polyline between every points is drawn |
| "F" | A fill area is drawn ('CF' draw a smooth fill area) |
| "C" | A smooth Curve is drawn |
| "*" | A Star is plotted at each point |
| "P" | Idem with the current marker |
| "B" | A Bar chart is drawn at each point |
| "1" | ylow=rwymin |
| "X+" | The X-axis is drawn on the top side of the plot. |
| "Y+" | The Y-axis is drawn on the right side of the plot. |
Several drawing options can be combined. In the following example the graph is drawn as a smooth curve (optiob "C") and with markers (option "P"). The option "A" request the definition of the axis.
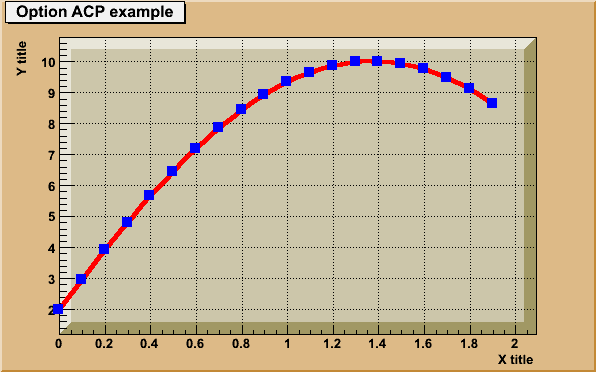
{
TCanvas *c1 = new TCanvas("c1","c1",200,10,600,400);
c1->SetFillColor(42);
c1->SetGrid();
const Int_t n = 20;
Double_t x[n], y[n];
for (Int_t i=0;i<n;i++) {
x[i] = i*0.1;
y[i] = 10*sin(x[i]+0.2);
}
gr = new TGraph(n,x,y);
gr->SetLineColor(2);
gr->SetLineWidth(4);
gr->SetMarkerColor(4);
gr->SetMarkerSize(1.5);
gr->SetMarkerStyle(21);
gr->SetTitle("Option ACP example");
gr->GetXaxis()->SetTitle("X title");
gr->GetYaxis()->SetTitle("Y title");
gr->Draw("ACP");
// TCanvas::Update() draws the frame, after which one can change it
c1->Update();
c1->GetFrame()->SetFillColor(21);
c1->GetFrame()->SetBorderSize(12);
c1->Modified();
return c1;
}Exclusion graphs
When a graph is painted with the option "C" or "L" it is possible to draw a filled area on one side of the line. This is useful to show exclusion zones.This drawing mode is activated when the absolute value of the graph line width (set thanks to SetLineWidth()) is greater than 99. In that case the line width number is interpreted as:
100*ff+ll = ffll
- The two digits number "ll" represent the normal line width
- The two digits number "ff" is the filled area width.
- The sign of "ffll" allows to flip the filled area from one side of the line to the other.
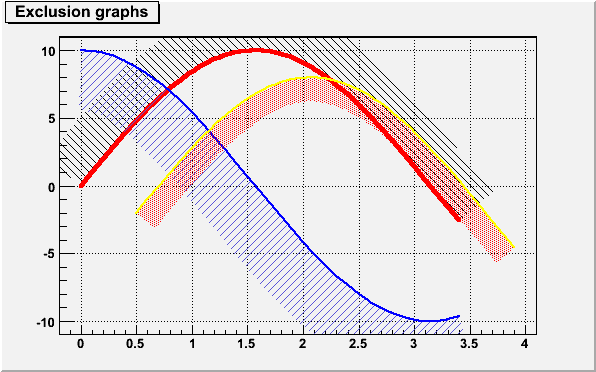
TCanvas *exclusiongraph() { // Draw three graphs with an exclusion zone. //Author: Olivier Couet TCanvas *c1 = new TCanvas("c1","Exclusion graphs examples",200,10,600,400); c1->SetGrid(); TMultiGraph *mg = new TMultiGraph(); mg->SetTitle("Exclusion graphs"); const Int_t n = 35; Double_t x1[n], x2[n], x3[n], y1[n], y2[n], y3[n]; for (Int_t i=0;i<n;i++) { x1[i] = i*0.1; x2[i] = x1[i]; x3[i] = x1[i]+.5; y1[i] = 10*sin(x1[i]); y2[i] = 10*cos(x1[i]); y3[i] = 10*sin(x1[i])-2; } TGraph *gr1 = new TGraph(n,x1,y1); gr1->SetLineColor(2); gr1->SetLineWidth(1504); gr1->SetFillStyle(3005); TGraph *gr2 = new TGraph(n,x2,y2); gr2->SetLineColor(4); gr2->SetLineWidth(-2002); gr2->SetFillStyle(3004); gr2->SetFillColor(9); TGraph *gr3 = new TGraph(n,x3,y3); gr3->SetLineColor(5); gr3->SetLineWidth(-802); gr3->SetFillStyle(3002); gr3->SetFillColor(2); mg->Add(gr1); mg->Add(gr2); mg->Add(gr3); mg->Draw("AC"); return c1; }
Graphs with error bars
Three classes are available to handle graphs with error bars: TGraphErrors, TGraphAsymmErrors and TGraphBentErrors. In addition to the drawing options previously described, the graphs with error bars can be drawn with the following extra options:
| "Z" | By default horizonthal and vertical small lines are drawn at the end of the error bars. If option "z" or "Z" is specified, these lines are not drawn. |
|---|---|
| ">" | An arrow is drawn at the end of the error bars. The size of the arrow is set to 2/3 of the marker size. |
| "|>" | A filled arrow is drawn at the end of the error bars. The size of the arrow is set to 2/3 of the marker size. |
| "X" | By default the error bars are drawn. If option "X" is specified, the errors are not drawn. The graph with errors in drawn like a normal graph. |
| "||" | Only the end vertical/horizonthal lines of the error bars are drawn. This option is interesting to superimpose systematic errors on top of a graph with statistical errors. |
| "[]" | Does the same as option "||" except that it draws additionnal tick marks at the end of the vertical/horizonthal lines. This makes less ambiguous plots in case several graphs are drawn on the same picture. |
| "2" | Error rectangles are drawn. |
| "3" | A filled area is drawn through the end points of the vertical error bars. |
| "4" | A smoothed filled area is drawn through the end points of the vertical error bars. |
gStyle->SetErrorX(dx) controls the size of the error along x. dx = 0 removes the error along x.
gStyle->SetEndErrorSize(np) controls the size of the lines at the end of the error bars (when option 1 is used). By default np=1. (np represents the number of pixels).
TGraphErrors
A TGraphErrors is a TGraph with error bars. The errors are defined along X and Y and are symmetric: The left and right errors are the same along X and the bottom and up errors are the same along Y.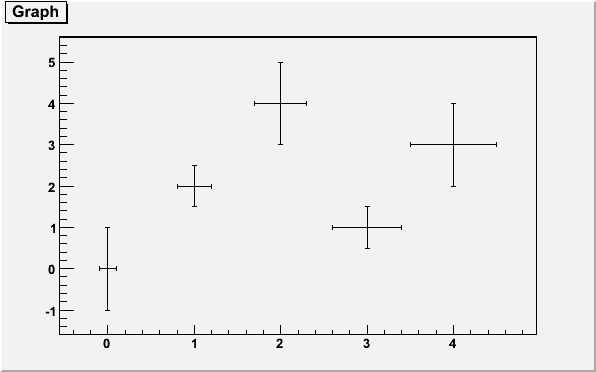
{
TCanvas *c4 = new TCanvas("c4","c4",200,10,600,400);
double x[] = {0, 1, 2, 3, 4};
double y[] = {0, 2, 4, 1, 3};
double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
double ey[] = {1, 0.5, 1, 0.5, 1};
TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
ge->Draw("ap");
return c4;
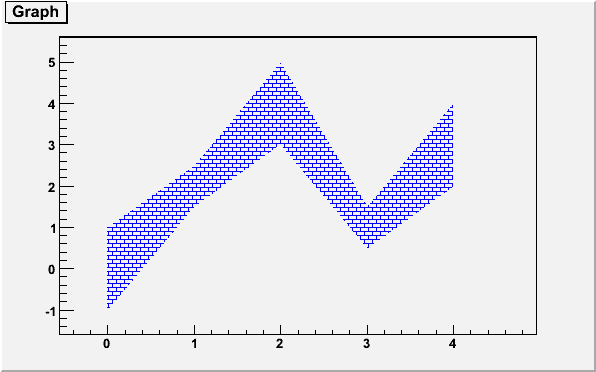
}
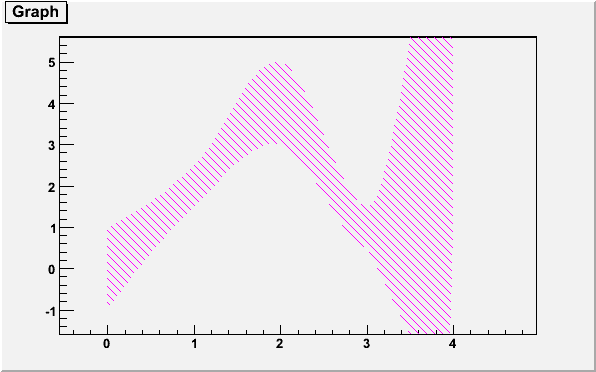
{
TCanvas *c41 = new TCanvas("c41","c41",200,10,600,400);
double x[] = {0, 1, 2, 3, 4};
double y[] = {0, 2, 4, 1, 3};
double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
double ey[] = {1, 0.5, 1, 0.5, 1};
TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
ge->SetFillColor(4);
ge->SetFillStyle(3010);
ge->Draw("a3");
return c41;
}
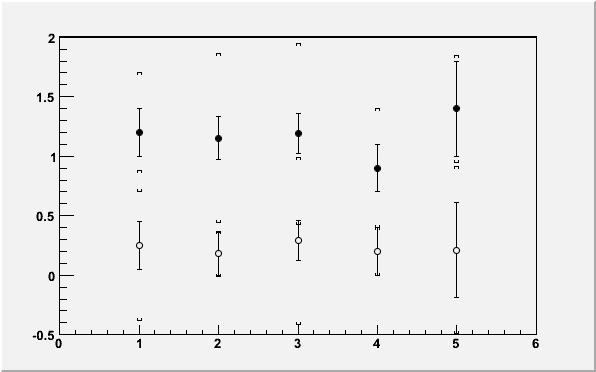
{
TCanvas *c42 = new TCanvas("c42","c42",200,10,600,400);
double x[] = {0, 1, 2, 3, 4};
double y[] = {0, 2, 4, 1, 3};
double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
double ey[] = {1, 0.5, 1, 0.5, 1};
TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
ge->SetFillColor(6);
ge->SetFillStyle(3005);
ge->Draw("a4");
return c42;
}
{
TCanvas *c43 = new TCanvas("c43","c43",200,10,600,400);
c43->DrawFrame(0., -0.5, 6., 2);
double x[5] = {1, 2, 3, 4, 5};
double zero[5] = {0, 0, 0, 0, 0};
// data set (1) with stat and sys errors
double y1[5] = {1.2, 1.15, 1.19, 0.9, 1.4};
double ey_stat1[5] = {0.2, 0.18, 0.17, 0.2, 0.4};
double ey_sys1[5] = {0.5, 0.71, 0.76, 0.5, 0.45};
// data set (2) with stat and sys errors
double y2[5] = {0.25, 0.18, 0.29, 0.2, 0.21};
double ey_stat2[5] = {0.2, 0.18, 0.17, 0.2, 0.4};
double ey_sys2[5] = {0.63, 0.19, 0.7, 0.2, 0.7};
// Now draw data set (1)
// We first have to draw it only with the stat errors
TGraphErrors *graph1 = new TGraphErrors(5, x, y1, zero, ey_stat1);
graph1->SetMarkerStyle(20);
graph1->Draw("P");
// Now we have to somehow depict the sys errors
TGraphErrors *graph1_sys = new TGraphErrors(5, x, y1, zero, ey_sys1);
graph1_sys->Draw("[]");
// Now draw data set (2)
// We first have to draw it only with the stat errors
TGraphErrors *graph2 = new TGraphErrors(5, x, y2, zero, ey_stat2);
graph2->SetMarkerStyle(24);
graph2->Draw("P");
// Now we have to somehow depict the sys errors
TGraphErrors *graph2_sys = new TGraphErrors(5, x, y2, zero, ey_sys2);
graph2_sys->Draw("[]");
return c43;
}TGraphAsymmErrors
A TGraphAsymmErrors is like a TGraphErrors but the errors defined along X and Y are not symmetric: The left and right errors are different along X and the bottom and up errors are different along Y.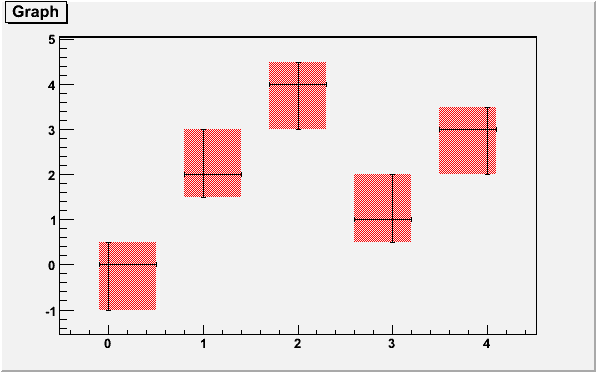
{
TCanvas *c2 = new TCanvas("c2","c2",200,10,600,400);
double ax[] = {0, 1, 2, 3, 4};
double ay[] = {0, 2, 4, 1, 3};
double aexl[] = {0.1, 0.2, 0.3, 0.4, 0.5};
double aexh[] = {0.5, 0.4, 0.3, 0.2, 0.1};
double aeyl[] = {1, 0.5, 1, 0.5, 1};
double aeyh[] = {0.5, 1, 0.5, 1, 0.5};
TGraphAsymmErrors* gae = new TGraphAsymmErrors(5, ax, ay, aexl, aexh, aeyl, aeyh);
gae->SetFillColor(2);
gae->SetFillStyle(3001);
gae->Draw("a2");
gae->Draw("p");
return c2;
}TGraphBentErrors
A TGraphBentErrors is like a TGraphAsymmErrors. An extra parameter allows to bent the error bars to better see them when several graphs are drawn on the same plot.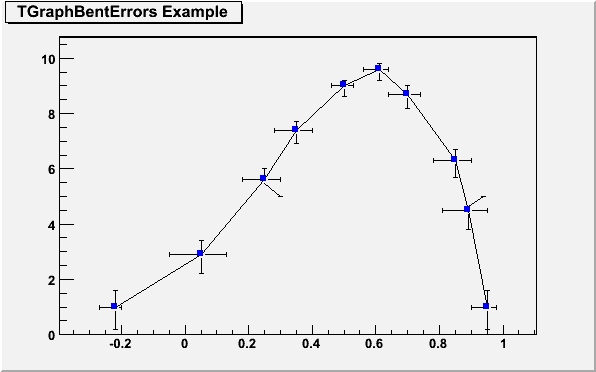
{
TCanvas *c3 = new TCanvas("c3","c3",200,10,600,400);
const Int_t n = 10;
Double_t x[n] = {-0.22, 0.05, 0.25, 0.35, 0.5, 0.61,0.7,0.85,0.89,0.95};
Double_t y[n] = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
Double_t exl[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Double_t eyl[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
Double_t exh[n] = {.02,.08,.05,.05,.03,.03,.04,.05,.06,.03};
Double_t eyh[n] = {.6,.5,.4,.3,.2,.2,.3,.4,.5,.6};
Double_t exld[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
Double_t eyld[n] = {.0,.0,.05,.0,.0,.0,.0,.0,.0,.0};
Double_t exhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
Double_t eyhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.05,.0};
TGraphBentErrors *gr = new TGraphBentErrors(n,x,y,exl,exh,eyl,eyh,exld,exhd,eyld,eyhd);
gr->SetTitle("TGraphBentErrors Example");
gr->SetMarkerColor(4);
gr->SetMarkerStyle(21);
gr->Draw("ALP");
return c3;
}TGraphPolar options
The drawing options for the polar graphs are the following values:| "O" | Polar labels are paint orthogonally to the polargram radius. |
|---|---|
| "P" | Polymarker are paint at each point position. |
| "E" | Paint error bars. |
| "F" | Paint fill area (closed polygon). |
| "A" | Force axis redrawing even if a polargram already exists. |
| "N" | Disable the display of the polar labels. |
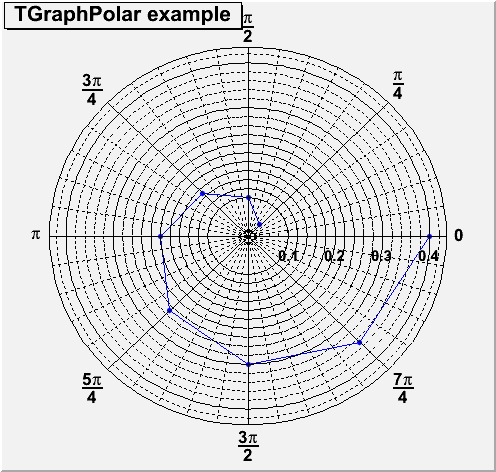
{
TCanvas *c1 = new TCanvas("c1","c1",500,500);
TGraphPolar * grP1 = new TGraphPolar();
grP1->SetTitle("TGraphPolar example");
grP1->SetPoint(0, (1*TMath::Pi())/4., 0.05);
grP1->SetPoint(1, (2*TMath::Pi())/4., 0.10);
grP1->SetPoint(2, (3*TMath::Pi())/4., 0.15);
grP1->SetPoint(3, (4*TMath::Pi())/4., 0.20);
grP1->SetPoint(4, (5*TMath::Pi())/4., 0.25);
grP1->SetPoint(5, (6*TMath::Pi())/4., 0.30);
grP1->SetPoint(6, (7*TMath::Pi())/4., 0.35);
grP1->SetPoint(7, (8*TMath::Pi())/4., 0.40);
grP1->SetMarkerStyle(20);
grP1->SetMarkerSize(1.);
grP1->SetMarkerColor(4);
grP1->SetLineColor(4);
grP1->Draw("ALP");
// Update, otherwise GetPolargram returns 0
c1->Update();
grP1->GetPolargram()->SetToRadian();
return c1;
}Function Members (Methods)
| TGraphPainter() | |
| TGraphPainter(const TGraphPainter&) | |
| virtual | ~TGraphPainter() |
| void | TObject::AbstractMethod(const char* method) const |
| virtual void | TObject::AppendPad(Option_t* option = "") |
| virtual void | TObject::Browse(TBrowser* b) |
| static TClass* | Class() |
| virtual const char* | TObject::ClassName() const |
| virtual void | TObject::Clear(Option_t* = "") |
| virtual TObject* | TObject::Clone(const char* newname = "") const |
| virtual Int_t | TObject::Compare(const TObject* obj) const |
| void | ComputeLogs(Int_t npoints, Int_t opt) |
| virtual void | TObject::Copy(TObject& object) const |
| virtual void | TObject::Delete(Option_t* option = "")MENU |
| virtual Int_t | TObject::DistancetoPrimitive(Int_t px, Int_t py) |
| virtual Int_t | DistancetoPrimitiveHelper(TGraph* theGraph, Int_t px, Int_t py) |
| virtual void | TObject::Draw(Option_t* option = "") |
| virtual void | TObject::DrawClass() constMENU |
| virtual TObject* | TObject::DrawClone(Option_t* option = "") constMENU |
| virtual void | DrawPanelHelper(TGraph* theGraph) |
| virtual void | TObject::Dump() constMENU |
| virtual void | TObject::Error(const char* method, const char* msgfmt) const |
| virtual void | TObject::Execute(const char* method, const char* params, Int_t* error = 0) |
| virtual void | TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0) |
| virtual void | TObject::ExecuteEvent(Int_t event, Int_t px, Int_t py) |
| virtual void | ExecuteEventHelper(TGraph* theGraph, Int_t event, Int_t px, Int_t py) |
| virtual void | TObject::Fatal(const char* method, const char* msgfmt) const |
| virtual TObject* | TObject::FindObject(const char* name) const |
| virtual TObject* | TObject::FindObject(const TObject* obj) const |
| virtual Option_t* | TObject::GetDrawOption() const |
| static Long_t | TObject::GetDtorOnly() |
| virtual const char* | TObject::GetIconName() const |
| virtual const char* | TObject::GetName() const |
| virtual char* | TObject::GetObjectInfo(Int_t px, Int_t py) const |
| virtual char* | GetObjectInfoHelper(TGraph* theGraph, Int_t px, Int_t py) const |
| static Bool_t | TObject::GetObjectStat() |
| virtual Option_t* | TObject::GetOption() const |
| static TVirtualGraphPainter* | TVirtualGraphPainter::GetPainter() |
| virtual const char* | TObject::GetTitle() const |
| virtual UInt_t | TObject::GetUniqueID() const |
| virtual Bool_t | TObject::HandleTimer(TTimer* timer) |
| virtual ULong_t | TObject::Hash() const |
| virtual void | TObject::Info(const char* method, const char* msgfmt) const |
| virtual Bool_t | TObject::InheritsFrom(const char* classname) const |
| virtual Bool_t | TObject::InheritsFrom(const TClass* cl) const |
| virtual void | TObject::Inspect() constMENU |
| void | TObject::InvertBit(UInt_t f) |
| virtual TClass* | IsA() const |
| virtual Bool_t | TObject::IsEqual(const TObject* obj) const |
| virtual Bool_t | TObject::IsFolder() const |
| Bool_t | TObject::IsOnHeap() const |
| virtual Bool_t | TObject::IsSortable() const |
| Bool_t | TObject::IsZombie() const |
| virtual void | TObject::ls(Option_t* option = "") const |
| void | TObject::MayNotUse(const char* method) const |
| virtual Bool_t | TObject::Notify() |
| static void | TObject::operator delete(void* ptr) |
| static void | TObject::operator delete(void* ptr, void* vp) |
| static void | TObject::operator delete[](void* ptr) |
| static void | TObject::operator delete[](void* ptr, void* vp) |
| void* | TObject::operator new(size_t sz) |
| void* | TObject::operator new(size_t sz, void* vp) |
| void* | TObject::operator new[](size_t sz) |
| void* | TObject::operator new[](size_t sz, void* vp) |
| TGraphPainter& | operator=(const TGraphPainter&) |
| virtual void | TObject::Paint(Option_t* option = "") |
| virtual void | PaintGraph(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt) |
| void | PaintGraphAsymmErrors(TGraph* theGraph, Option_t* option) |
| void | PaintGraphBentErrors(TGraph* theGraph, Option_t* option) |
| void | PaintGraphErrors(TGraph* theGraph, Option_t* option) |
| virtual void | PaintGrapHist(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt) |
| void | PaintGraphPolar(TGraph* theGraph, Option_t* option) |
| void | PaintGraphQQ(TGraph* theGraph, Option_t* option) |
| void | PaintGraphSimple(TGraph* theGraph, Option_t* option) |
| virtual void | PaintHelper(TGraph* theGraph, Option_t* option) |
| void | PaintPolyLineHatches(TGraph* theGraph, Int_t n, const Double_t* x, const Double_t* y) |
| virtual void | PaintStats(TGraph* theGraph, TF1* fit) |
| virtual void | TObject::Pop() |
| virtual void | TObject::Print(Option_t* option = "") const |
| virtual Int_t | TObject::Read(const char* name) |
| virtual void | TObject::RecursiveRemove(TObject* obj) |
| void | TObject::ResetBit(UInt_t f) |
| virtual void | TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU |
| virtual void | TObject::SavePrimitive(basic_ostream<char,char_traits<char> >& out, Option_t* option = "") |
| void | TObject::SetBit(UInt_t f) |
| void | TObject::SetBit(UInt_t f, Bool_t set) |
| virtual void | TObject::SetDrawOption(Option_t* option = "")MENU |
| static void | TObject::SetDtorOnly(void* obj) |
| static void | TObject::SetObjectStat(Bool_t stat) |
| static void | TVirtualGraphPainter::SetPainter(TVirtualGraphPainter* painter) |
| virtual void | TObject::SetUniqueID(UInt_t uid) |
| virtual void | ShowMembers(TMemberInspector& insp, char* parent) |
| void | Smooth(TGraph* theGraph, Int_t npoints, Double_t* x, Double_t* y, Int_t drawtype) |
| virtual void | Streamer(TBuffer& b) |
| void | StreamerNVirtual(TBuffer& b) |
| virtual void | TObject::SysError(const char* method, const char* msgfmt) const |
| Bool_t | TObject::TestBit(UInt_t f) const |
| Int_t | TObject::TestBits(UInt_t f) const |
| virtual void | TObject::UseCurrentStyle() |
| virtual void | TObject::Warning(const char* method, const char* msgfmt) const |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const |
| virtual void | TObject::DoError(int level, const char* location, const char* fmt, va_list va) const |
| void | TObject::MakeZombie() |
Data Members
| enum TObject::EStatusBits { | kCanDelete | |
| kMustCleanup | ||
| kObjInCanvas | ||
| kIsReferenced | ||
| kHasUUID | ||
| kCannotPick | ||
| kNoContextMenu | ||
| kInvalidObject | ||
| }; | ||
| enum TObject::[unnamed] { | kIsOnHeap | |
| kNotDeleted | ||
| kZombie | ||
| kBitMask | ||
| kSingleKey | ||
| kOverwrite | ||
| kWriteDelete | ||
| }; |
Class Charts
Function documentation
npoints : Number of points in gxwork and in gywork.
- opt = 1 CompulteLogs is called from PaintGrapHist
- opt = 0 CompulteLogs is called from PaintGraph
Compute the closest distance of approach from point px,py to this line. The distance is computed in pixels units.
This member function is called when a graph is clicked with the locator.
If the left mouse button is clicked on one of the line end points, this point follows the cursor until button is released.
If the middle mouse button clicked, the line is moved parallel to itself until the button is released.
Input parameters:
- npoints : Number of points in X or in Y.
- x[npoints] or x[0] : x coordinates or (xmin,xmax).
- y[npoints] or y[0] : y coordinates or (ymin,ymax).
- chopt : Option.
The aspect of the graph is done according to the value of the chopt.
| "R" |
Graph is drawn horizontaly, parallel to X axis. (default is vertically,
parallel to Y axis)
If option R is selected the user must give:
|
|---|---|
| "L" | A simple polyline beetwen every points is drawn |
| "H" | An Histogram with equidistant bins is drawn as a polyline. |
| "F" | An histogram with equidistant bins is drawn as a fill area. Contour is not drawn unless chopt='H' is also selected.. |
| "N" | Non equidistant bins (default is equidistant) If N is the number of channels array X and Y must be dimensionned as follow: If option R is not selected (default) then the user must give: (N+1) values for X (limits of channels). N values for Y, one for each channel. Otherwise the user must give: (N+1) values for Y (limits of channels). N values for X, one for each channel. |
| "F1" | Idem as 'F' except that fill area is no more reparted arround axis X=0 or Y=0 . |
| "F2" | Draw a Fill area polyline connecting the center of bins |
| "C" | A smooth Curve is drawn. |
| "*" | A Star is plotted at the center of each bin. |
| "P" | Idem with the current marker |
| "P0" | Idem with the current marker. Empty bins also drawn |
| "B" | A Bar chart with equidistant bins is drawn as fill areas (Contours are drawn). |
| "9" | Force graph to be drawn in high resolution mode. By default, the graph is drawn in low resolution in case the number of points is greater than the number of pixels in the current pad. |
| "][" | "Cutoff" style. When this option is selected together with H option, the first and last vertical lines of the histogram are not drawn. |
The original code come from an underlaying routine for Draw based on the CERN GD3 routine TVIPTE:
Author - Marlow etc. Modified by - P. Ward Date - 3.10.1973This method draws a smooth tangentially continuous curve through the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I)) the curve is approximated by a polygonal arc of short vectors . the data points can represent open curves, P(1) != P(N) or closed curves P(2) == P(N) . If a tangential discontinuity at P(I) is required , then set P(I)=P(I+1) . loops are also allowed .
Reference Marlow and Powell,Harwell report No.R.7092.1972 MCCONALOGUE,Computer Journal VOL.13,NO4,NOV1970Pp392 6
- npoints : Number of data points.
- x : Abscissa
- y : Ordinate