Abstract
ROOT is a software framework for data analysis and I/O: a powerful tool to cope with the demanding tasks typical of state of the art scientific data analysis. Among its prominent features are an advanced graphical user interface, ideal for interactive analysis, an interpreter for the C++ programming language, for rapid and efficient prototyping and a persistency mechanism for C++ objects, used also to write every year petabytes of data recorded by the Large Hadron Collider experiments. This introductory guide illustrates the main features of ROOT which are relevant for the typical problems of data analysis: input and plotting of data from measurements and fitting of analytical functions.
Original Authors - D. Piparo - G. Quast - M. Zeise
Welcome to data analysis!
Comparison of measurements to theoretical models is one of the standard tasks in experimental physics. In the most simple case, a “model” is just a function providing predictions of measured data. Very often, the model depends on parameters. Such a model may simply state “the current I is proportional to the voltage U”, and the task of the experimentalist consists of determining the resistance, R, from a set of measurements.
As a first step, a visualisation of the data is needed. Next, some manipulations typically have to be applied, e.g. corrections or parameter transformations. Quite often, these manipulations are complex ones, and a powerful library of mathematical functions and procedures should be provided - think for example of an integral or peak-search or a Fourier transformation applied to an input spectrum to obtain the actual measurement described by the model.
One specialty of experimental physics are the inevitable uncertainties affecting each measurement, and visualisation tools have to include these. In subsequent analysis, the statistical nature of the errors must be handled properly.
As the last step, measurements are compared to models, and free model parameters need to be determined in this process. See Figure 1.1 for an example of a function (model) fit to data points. Several standard methods are available, and a data analysis tool should provide easy access to more than one of them. Means to quantify the level of agreement between measurements and model must also be available.
Quite often, the data volume to be analyzed is large - think of fine-granular measurements accumulated with the aid of computers. A usable tool therefore must contain easy-to-use and efficient methods for storing and handling data.
In Quantum mechanics, models typically only predict the probability density function (“pdf”) of measurements depending on a number of parameters, and the aim of the experimental analysis is to extract the parameters from the observed distribution of frequencies at which certain values of the measurement are observed. Measurements of this kind require means to generate and visualize frequency distributions, so-called histograms, and stringent statistical treatment to extract the model parameters from purely statistical distributions.
Simulation of expected data is another important aspect in data analysis. By repeated generation of “pseudo-data”, which are analysed in the same manner as intended for the real data, analysis procedures can be validated or compared. In many cases, the distribution of the measurement errors is not precisely known, and simulation offers the possibility to test the effects of different assumptions.
A powerful software framework addressing all of the above requirements is ROOT, an open source project coordinated by the European Organisation for Nuclear Research, CERN in Geneva.
ROOT is very flexible and provides both a programming interface to use in own applications and a graphical user interface for interactive data analysis. The purpose of this document is to serve as a beginners guide and provides extendable examples for your own use cases, based on typical problems addressed in student labs. This guide will hopefully lay the ground for more complex applications in your future scientific work building on a modern, state-of the art tool for data analysis.
This guide in form of a tutorial is intended to introduce you quickly to the ROOT package. This goal will be accomplished using concrete examples, according to the “learning by doing” principle. Also because of this reason, this guide cannot cover all the complexity of the ROOT package. Nevertheless, once you feel confident with the concepts presented in the following chapters, you will be able to appreciate the ROOT Users Guide (The Root Users Guide 2020) and navigate through the Class Reference (The Root Reference Guide 2023) to find all the details you might be interested in. You can even look at the code itself, since ROOT is a free, open-source product. Use these documents in parallel to this tutorial!
The ROOT Data Analysis Framework itself is written in and heavily relies on the C++ programming language: some knowledge about C++ is required. Jus take advantage from the immense available literature about C++ if you do not have any idea of what this language is about.
ROOT is available for many platforms (Linux, Mac OS X, Windows…), but in this guide we will implicitly assume that you are using Linux. The first thing you need to do with ROOT is install it, don’t you ? Obtaining the latest ROOT version is straightforward. Just seek the “Pro” version on this webpage http://root.cern.ch/downloading-root. You will find precompiled versions for the different architectures, or the ROOT source code to compile yourself. Just pick up the flavour you need and follow the installation instructions.
Let’s dive into ROOT!
Now that you have installed ROOT, what’s this interactive shell thing you’re running ? It’s like this: ROOT leads a double life. It has an interpreter for macros (Cling (“What is Cling” 2015)) that you can run from the command line or run like applications. But it is also an interactive shell that can evaluate arbitrary statements and expressions. This is extremely useful for debugging, quick hacking and testing. Let us first have a look at some very simple examples.
You can even use the ROOT interactive shell in lieu of a calculator! Launch the ROOT interactive shell with the command
on your Linux box. The prompt should appear shortly:
and let’s dive in with the steps shown here:
root [0] 1+1
(int) 2
root [1] 2*(4+2)/12.
(double) 1.000000
root [2] sqrt(3.)
(double) 1.732051
root [3] 1 > 2
(bool) false
root [4] TMath::Pi()
(double) 3.141593
root [5] TMath::Erf(.2)
(double) 0.222703Not bad. You can see that ROOT offers you the possibility not only to type in C++ statements, but also advanced mathematical functions, which live in the TMath namespace.
Now let’s do something more elaborated. A numerical example with the well known geometrical series:
root [6] double x=.5
(double) 0.500000
root [7] int N=30
(int) 30
root [8] double geom_series=0
(double) 0.000000
root [9] for (int i=0;i<N;++i)geom_series+=TMath::Power(x,i)
root [10] cout << TMath::Abs(geom_series - (1-TMath::Power(x,N-1))/(1-x)) <<endl;
1.86265e-09Here we made a step forward. We even declared variables and used a for control structure. Note that there are some subtle differences between Cling and the standard C++ language. You do not need the “;” at the end of line in interactive mode – try the difference e.g. using the command at line root [6].
Behind the ROOT prompt there is an interpreter based on a real compiler toolkit: LLVM. It is therefore possible to exercise many features of C++ and the standard library. For example in the following snippet we define a lambda function, a vector and we sort it in different ways:
root [0] using doubles = std::vector<double>;
root [1] auto pVec = [](const doubles& v){for (auto&& x:v) cout << x << endl;};
root [2] doubles v{0,3,5,4,1,2};
root [3] pVec(v);
0
3
5
4
1
2
root [4] std::sort(v.begin(),v.end());
root [5] pVec(v);
0
1
2
3
4
5
root [6] std::sort(v.begin(),v.end(),[](double a, double b){return a>b;});
root [7] pVec(v);
5
4
3
2
1
0Or, if you prefer random number generation:
root [0] std::default_random_engine generator;
root [1] std::normal_distribution<double> distribution(0.,1.);
root [2] distribution(generator)
(std::normal_distribution<double>::result_type) -1.219658e-01
root [3] distribution(generator)
(std::normal_distribution<double>::result_type) -1.086818e+00
root [4] distribution(generator)
(std::normal_distribution<double>::result_type) 6.842899e-01Impressive isn’t it?
Using one of ROOT’s powerful classes, here TF1,1 will allow us to display a function of one variable, x. Try the following:
f1 is an instance of a TF1 class, the arguments are used in the constructor; the first one of type string is a name to be entered in the internal ROOT memory management system, the second string type parameter defines the function, here sin(x)/x, and the two parameters of type double define the range of the variable x. The Draw() method, here without any parameters, displays the function in a window which should pop up after you typed the above two lines.
A slightly extended version of this example is the definition of a function with parameters, called [0], [1] and so on in the ROOT formula syntax. We now need a way to assign values to these parameters; this is achieved with the method SetParameter(<parameter_number>,<parameter_value>) of class TF1. Here is an example:
root [13] TF1 f2("f2","[0]*sin([1]*x)/x",0.,10.);
root [14] f2.SetParameter(0,1);
root [15] f2.SetParameter(1,1);
root [16] f2.Draw();Of course, this version shows the same results as the initial one. Try playing with the parameters and plot the function again. The class TF1 has a large number of very useful methods, including integration and differentiation. To make full use of this and other ROOT classes, visit the documentation on the Internet under https://root.cern/doc/master/. Formulae in ROOT are evaluated using the class TFormula, so also look up the relevant class documentation for examples, implemented functions and syntax.
You should definitely download this guide to your own system to have it at you disposal whenever you need it.
To extend a little bit on the above example, consider a more complex function you would like to define. You can also do this using standard C or C++ code.
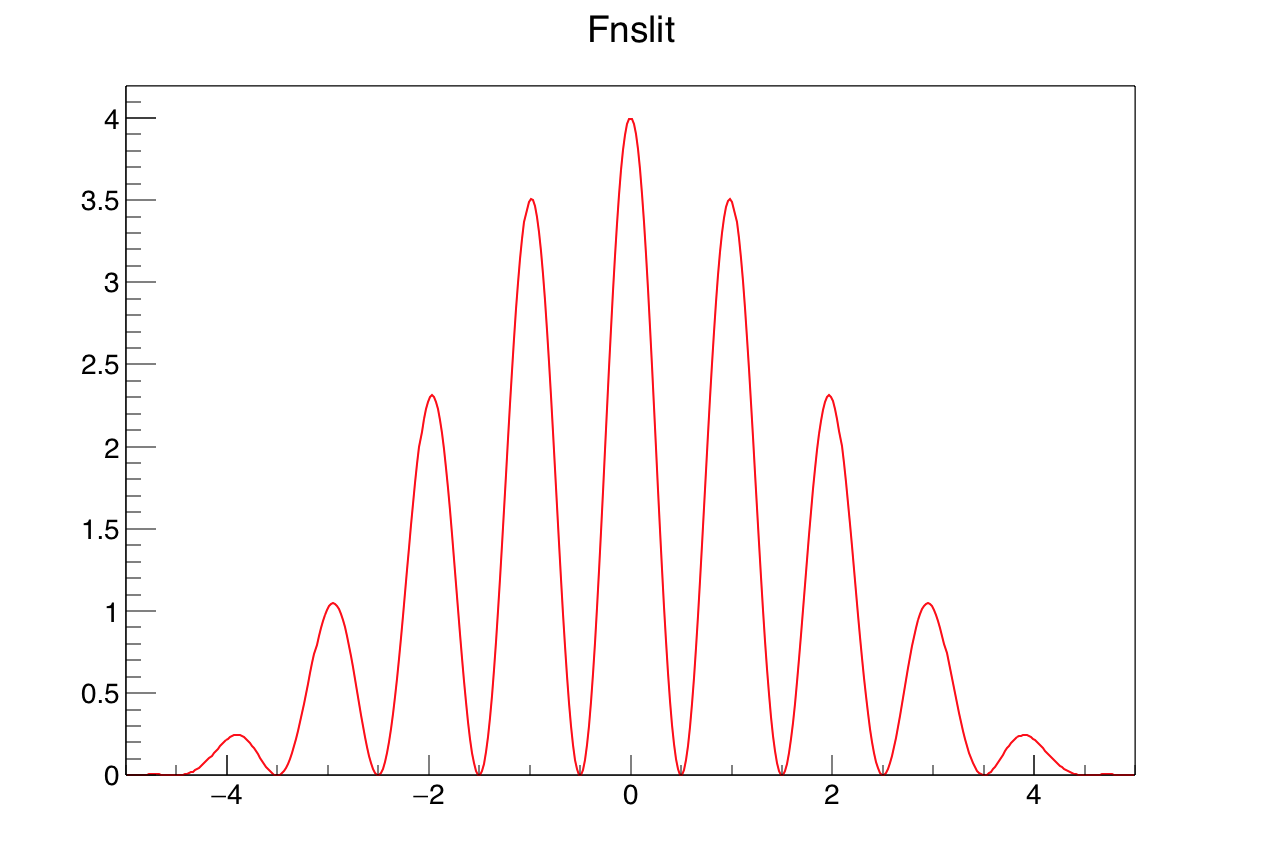
Consider the example below, which calculates and displays the interference pattern produced by light falling on a multiple slit. Please do not type in the example below at the ROOT command line, there is a much simpler way: Make sure you have the file slits.C on disk, and type root slits.C in the shell. This will start root and make it read the “macro” slits.C, i.e. all the lines in the file will be executed one after the other.
// Example drawing the interference pattern of light
// falling on a grid with n slits and ratio r of slit
// width over distance between slits.
auto pi = TMath::Pi();
// function code in C
double single(double *x, double *par) {
return pow(sin(pi*par[0]*x[0])/(pi*par[0]*x[0]),2);
}
double nslit0(double *x,double *par){
return pow(sin(pi*par[1]*x[0])/sin(pi*x[0]),2);
}
double nslit(double *x, double *par){
return single(x,par) * nslit0(x,par);
}
// This is the main program
void slits() {
float r,ns;
// request user input
cout << "slit width / g ? ";
scanf("%f",&r);
cout << "# of slits? ";
scanf("%f",&ns);
cout <<"interference pattern for "<< ns
<<" slits, width/distance: "<<r<<endl;
// define function and set options
TF1 *Fnslit = new TF1("Fnslit",nslit,-5.001,5.,2);
Fnslit->SetNpx(500);
// set parameters, as read in above
Fnslit->SetParameter(0,r);
Fnslit->SetParameter(1,ns);
// draw the interference pattern for a grid with n slits
Fnslit->Draw();
}
The example first asks for user input, namely the ratio of slit width over slit distance, and the number of slits. After entering this information, you should see the graphical output as is shown in Figure 2.1.
This is a more complicated example than the ones we have seen before, so spend some time analysing it carefully, you should have understood it before continuing. Let us go through it in detail:
Lines 7-18 define the necessary functions in C++ code, split into three separate functions, as suggested by the problem considered. The full interference pattern is given by the product of a function depending on the ratio of the width and distance of the slits, and a second one depending on the number of slits. More important for us here is the definition of the interface of these functions to make them usable for the ROOT class TF1: the first argument is the pointer to x, the second one points to the array of parameters.
The main program starts at line 21 with the definition of a function slits() of type void. After asking for user input, a ROOT function is defined using the C-type function given in the beginning. We can now use all methods of the TF1 class to control the behaviour of our function – nice, isn’t it ?
If you like, you can easily extend the example to also plot the interference pattern of a single slit, using function double single, or of a grid with narrow slits, function double nslit0, in TF1 instances.
Here, we used a macro, some sort of lightweight program, that the interpreter distributed with ROOT, Cling, is able to execute. This is a rather extraordinary situation, since C++ is not natively an interpreted language! There is much more to say: chapter is indeed dedicated to macros.
One more remark at this point: as every command you type into ROOT is usually interpreted by Cling, an “escape character” is needed to pass commands to ROOT directly. This character is the dot at the beginning of a line:
This is a selection of the most common commands.
quit root, simply type .q or .quit or .exit
obtain the full list of commands, use .? or .help
access the shell of the operating system, type .!<OS_command>; try, e.g. .!ls or .!pwd
execute a macro, enter .x <file_name>; in the above example, you might have used .x slits.C at the ROOT prompt
load a macro, type .L <file_name>; in the above example, you might instead have used the command .L slits.C followed by the function call slits();. Note that after loading a macro all functions and procedures defined therein are available at the ROOT prompt.
compile a macro, type .L <file_name>+; ROOT is able to manage for you the C++ compiler behind the scenes and to produce machine code starting from your macro. One could decide to compile a macro in order to obtain better performance or to get nearer to the production environment.
To display measurements in ROOT, including errors, there exists a powerful class TGraphErrors with different types of constructors. In the example here, we use data from the file ExampleData.txt in text format:
You should see the output shown in Figure 2.2.

Make sure the file ExampleData.txt is available in the directory from which you started ROOT. Inspect this file now with your favourite editor, or use the command less ExampleData.txt to inspect the file, you will see that the format is very simple and easy to understand. Lines beginning with # are ignored. It is very convenient to add some comments about the type of data. The data itself consist of lines with four real numbers each, representing the x- and y- coordinates and their errors of each data point.
The argument of the method Draw("AP") is important here. Behind the scenes, it tells the TGraphPainter class to show the axes and to plot markers at the x and y positions of the specified data points. Note that this simple example relies on the default settings of ROOT, concerning the size of the canvas holding the plot, the marker type and the line colours and thickness used and so on. In a well-written, complete example, all this would need to be specified explicitly in order to obtain nice and well readable results. A full chapter on graphs will explain many more of the features of the class TGraphErrors and its relation to other ROOT classes in much more detail.
Frequency distributions in ROOT are handled by a set of classes derived from the histogram class TH1, in our case TH1F. The letter F stands for “float”, meaning that the data type float is used to store the entries in one histogram bin.
root [0] TF1 efunc("efunc","exp([0]+[1]*x)",0.,5.);
root [1] efunc.SetParameter(0,1);
root [2] efunc.SetParameter(1,-1);
root [3] TH1F h("h","example histogram",100,0.,5.);
root [4] for (int i=0;i<1000;i++) {h.Fill(efunc.GetRandom());}
root [5] h.Draw();The first three lines of this example define a function, an exponential in this case, and set its parameters. In line 3 a histogram is instantiated, with a name, a title, a certain number of bins (100 of them, equidistant, equally sized) in the range from 0 to 5.

We use yet another new feature of ROOT to fill this histogram with data, namely pseudo-random numbers generated with the method TF1::GetRandom, which in turn uses an instance of the ROOT class TRandom created when ROOT is started. Data is entered in the histogram at line 4 using the method TH1F::Fill in a loop construct. As a result, the histogram is filled with 1000 random numbers distributed according to the defined function. The histogram is displayed using the method TH1F::Draw(). You may think of this example as repeated measurements of the life time of a quantum mechanical state, which are entered into the histogram, thus giving a visual impression of the probability density distribution. The plot is shown in Figure 2.3.
Note that you will not obtain an identical plot when executing the lines above, depending on how the random number generator is initialised.
The class TH1F does not contain a convenient input format from plain text files. The following lines of C++ code do the job. One number per line stored in the text file “expo.dat” is read in via an input stream and filled in the histogram until end of file is reached.
root [1] TH1F h("h","example histogram",100,0.,5.);
root [2] ifstream inp; double x;
root [3] inp.open("expo.dat");
root [4] while (inp >> x) { h.Fill(x); }
root [5] h.Draw();
root [6] inp.close();Histograms and random numbers are very important tools in statistical data analysis, a whole chapter will be dedicated to this topic.
Look at one of your plots again and move the mouse across. You will notice that this is much more than a static picture, as the mouse pointer changes its shape when touching objects on the plot. When the mouse is over an object, a right-click opens a pull-down menu displaying in the top line the name of the ROOT class you are dealing with, e.g. TCanvas for the display window itself, TFrame for the frame of the plot, TAxis for the axes, TPaveText for the plot name. Depending on which plot you are investigating, menus for the ROOT classes TF1, TGraphErrors or TH1F will show up when a right-click is performed on the respective graphical representations. The menu items allow direct access to the members of the various classes, and you can even modify them, e.g. change colour and size of the axis ticks or labels, the function lines, marker types and so on. Try it!
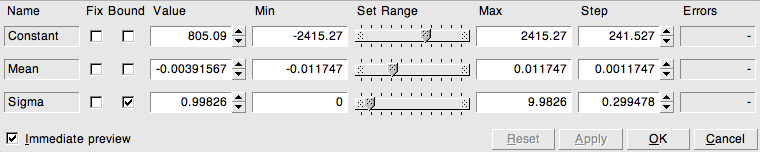
You will probably like the following: in the output produced by the example slits.C, right-click on the function line and select “SetLineAttributes”, then left-click on “Set Parameters”. This gives access to a panel allowing you to interactively change the parameters of the function, as shown in Figure 2.4. Change the slit width, or go from one to two and then three or more slits, just as you like. When clicking on “Apply”, the function plot is updated to reflect the actual value of the parameters you have set.
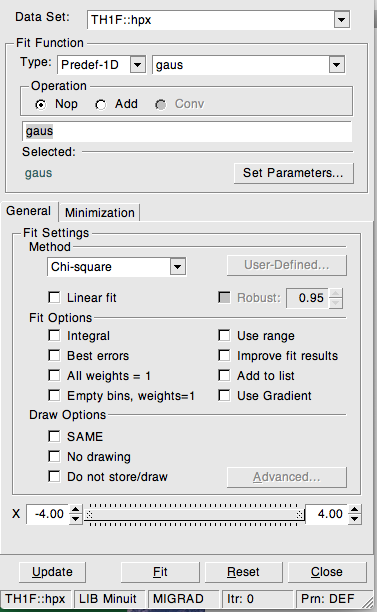
Another very useful interactive tool is the FitPanel, available for the classes TGraphErrors and TH1F. Predefined fit functions can be selected from a pull-down menu, including “gaus”, “expo” and “pol0” - “pol9” for Gaussian and exponential functions or polynomials of degree 0 to 9, respectively. In addition, user-defined functions using the same syntax as for functions with parameters are possible.
After setting the initial parameters, a fit of the selected function to the data of a graph or histogram can be performed and the result displayed on the plot. The fit panel is shown in Figure 2.5. The fit panel has a number of control options to select the fit method, fix or release individual parameters in the fit, to steer the level of output printed on the console, or to extract and display additional information like contour lines showing parameter correlations. As function fitting is of prime importance in any kind of data analysis, this topic will again show up later.
If you are satisfied with your plot, you probably want to save it. Just close all selector boxes you opened previously and select the menu item Save as... from the menu line of the window. It will pop up a file selector box to allow you to choose the format, file name and target directory to store the image. There is one very noticeable feature here: you can store a plot as a root macro! In this macro, you find the C++ representation of all methods and classes involved in generating the plot. This is a valuable source of information for your own macros, which you will hopefully write after having worked through this tutorial.
Using ROOT’s interactive capabilities is useful for a first exploration of possibilities. Other ROOT classes you will encounter in this tutorial have such graphical interfaces. We will not comment further on this, just be aware of the existence of ROOT’s interactive features and use them if you find them convenient. Some trial-and-error is certainly necessary to find your way through the huge number of menus and parameter settings.
At this point of the guide, some basic questions could have already come to your mind. We will try to clarify some of them with further explanations in the following.
In the official ROOT documentation, you find special data types replacing the normal ones, e.g. Double_t, Float_t or Int_t replacing the standard double, float or int types. Using the ROOT types makes it easier to port code between platforms (64/32 bit) or operating systems (windows/Linux), as these types are mapped to suitable ones in the ROOT header files. If you want adaptive code of this type, use the ROOT type declarations. However, usually you do not need such adaptive code, and you can safely use the standard C type declarations for your private code, as we did and will do throughout this guide. If you intend to become a ROOT developer, however, you better stick to the official coding rules!
The behaviour of a ROOT session can be tailored with the options in the .rootrc file. Examples of the tunable parameters are the ones related to the operating and window system, to the fonts to be used, to the location of start-up files. At start-up, ROOT looks for a .rootrc file in the following order:
./.rootrc //local directory
$HOME/.rootrc //user directory
$ROOTSYS/etc/system.rootrc //global ROOT directory
If more than one .rootrc files are found in the search paths above, the options are merged, with precedence local, user, global. The parsing and interpretation of this file is handled by the ROOT class TEnv. Have a look to its documentation if you need such rather advanced features. The file .rootrc defines the location of two rather important files inspected at start-up: rootalias.C and rootlogon.C. They can contain code that needs to be loaded and executed at ROOT startup. rootalias.C is only loaded and best used to define some often used functions. rootlogon.C contains code that will be executed at startup: this file is extremely useful for example to pre-load a custom style for the plots created with ROOT. This is done most easily by creating a new TStyle object with your preferred settings, as described in the class reference guide, and then use the command gROOT->SetStyle("MyStyleName"); to make this new style definition the default one. As an example, have a look in the file rootlogon.C coming with this tutorial. Another relevant file is rootlogoff.C that it called when the session is finished.
Every command typed at the ROOT prompt is stored in a file .root_hist in your home directory. ROOT uses this file to allow for navigation in the command history with the up-arrow and down-arrow keys. It is also convenient to extract successful ROOT commands with the help of a text editor for use in your own macros.
All global pointers in ROOT begin with a small “g”. Some of them were already implicitly introduced (for example in the section Configure ROOT at start-up). The most important among them are presented in the following:
gROOT: the gROOT variable is the entry point to the ROOT system. Technically it is an instance of the TROOT class. Using the gROOT pointer one has access to basically every object created in a ROOT based program. The TROOT object is essentially a container of several lists pointing to the main ROOT objects.
gStyle: By default ROOT creates a default style that can be accessed via the gStyle pointer. This class includes functions to set some of the following object attributes.
gSystem: An instance of a base class defining a generic interface to the underlying Operating System, in our case TUnixSystem.
gInterpreter: The entry point for the ROOT interpreter. Technically an abstraction level over a singleton instance of TCling.
At this point you have already learnt quite a bit about some basic features of ROOT.
Please move on to become an expert!
You know how other books go on and on about programming fundamentals and finally work up to building a complete, working program ? Let’s skip all that. In this guide, we will describe macros executed by the ROOT C++ interpreter Cling.
It is relatively easy to compile a macro, either as a pre-compiled library to load into ROOT, or as a stand-alone application, by adding some include statements for header file or some “dressing code” to any macro.
If you have a number of lines which you were able to execute at the ROOT prompt, they can be turned into a ROOT macro by giving them a name which corresponds to the file name without extension. The general structure for a macro stored in file MacroName.C is
The macro is executed by typing
at the system prompt, or executed using .x
at the ROOT prompt. or it can be loaded into a ROOT session and then be executed by typing
at the ROOT prompt. Note that more than one macro can be loaded this way, as each macro has a unique name in the ROOT name space. A small set of options can help making your plot nicer.
gROOT->SetStyle("Plain"); // set plain TStyle
gStyle->SetOptStat(111111); // draw statistics on plots,
// (0) for no output
gStyle->SetOptFit(1111); // draw fit results on plot,
// (0) for no ouput
gStyle->SetPalette(57); // set color map
gStyle->SetOptTitle(0); // suppress title box
...Next, you should create a canvas for graphical output, with size, subdivisions and format suitable to your needs, see documentation of class TCanvas:
TCanvas c1("c1","<Title>",0,0,400,300); // create a canvas, specify position and size in pixels
c1.Divide(2,2); //set subdivisions, called pads
c1.cd(1); //change to pad 1 of canvas c1These parts of a well-written macro are pretty standard, and you should remember to include pieces of code like in the examples above to make sure your plots always look as you had intended.
Below, in section Interpretation and Compilation, some more code fragments will be shown, allowing you to use the system compiler to compile macros for more efficient execution, or turn macros into stand-alone applications linked against the ROOT libraries.
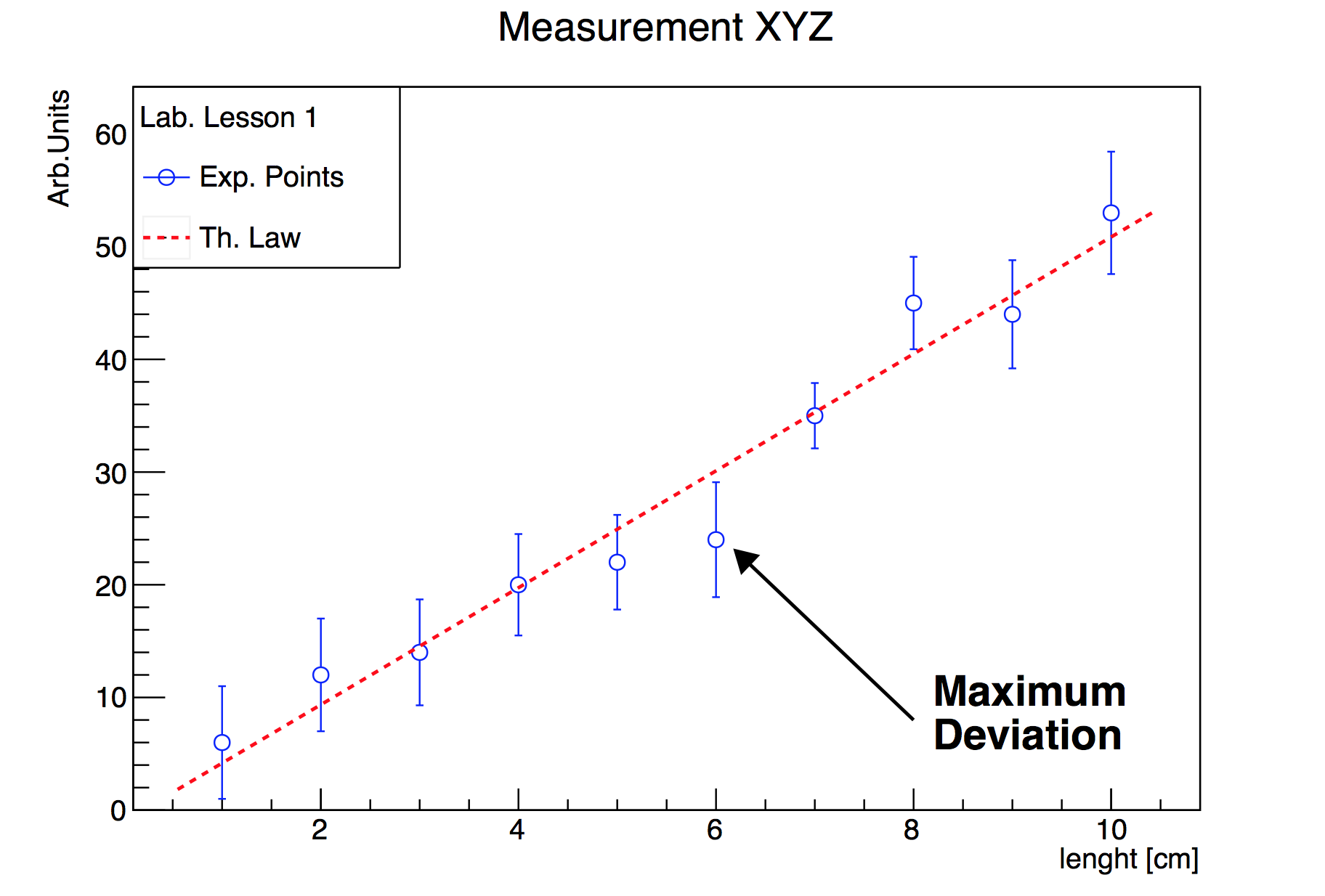
Let us now look at a rather complete example of a typical task in data analysis, a macro that constructs a graph with errors, fits a (linear) model to it and saves it as an image. To run this macro, simply type in the shell:
The code is built around the ROOT class TGraphErrors, which was already introduced previously. Have a look at it in the class reference guide, where you will also find further examples. The macro shown below uses additional classes, TF1 to define a function, TCanvas to define size and properties of the window used for our plot, and TLegend to add a nice legend. For the moment, ignore the commented include statements for header files, they will only become important at the end in section Interpretation and Compilation.
// Builds a graph with errors, displays it and saves it as
// image. First, include some header files
// (not necessary for Cling)
#include "TCanvas.h"
#include "TROOT.h"
#include "TGraphErrors.h"
#include "TF1.h"
#include "TLegend.h"
#include "TArrow.h"
#include "TLatex.h"
void macro1(){
// The values and the errors on the Y axis
const int n_points=10;
double x_vals[n_points]=
{1,2,3,4,5,6,7,8,9,10};
double y_vals[n_points]=
{6,12,14,20,22,24,35,45,44,53};
double y_errs[n_points]=
{5,5,4.7,4.5,4.2,5.1,2.9,4.1,4.8,5.43};
// Instance of the graph
TGraphErrors graph(n_points,x_vals,y_vals,nullptr,y_errs);
graph.SetTitle("Measurement XYZ;length [cm];Arb.Units");
// Make the plot estetically better
graph.SetMarkerStyle(kOpenCircle);
graph.SetMarkerColor(kBlue);
graph.SetLineColor(kBlue);
// The canvas on which we'll draw the graph
auto mycanvas = new TCanvas();
// Draw the graph !
graph.DrawClone("APE");
// Define a linear function
TF1 f("Linear law","[0]+x*[1]",.5,10.5);
// Let's make the function line nicer
f.SetLineColor(kRed); f.SetLineStyle(2);
// Fit it to the graph and draw it
graph.Fit(&f);
f.DrawClone("Same");
// Build and Draw a legend
TLegend leg(.1,.7,.3,.9,"Lab. Lesson 1");
leg.SetFillColor(0);
graph.SetFillColor(0);
leg.AddEntry(&graph,"Exp. Points");
leg.AddEntry(&f,"Th. Law");
leg.DrawClone("Same");
// Draw an arrow on the canvas
TArrow arrow(8,8,6.2,23,0.02,"|>");
arrow.SetLineWidth(2);
arrow.DrawClone();
// Add some text to the plot
TLatex text(8.2,7.5,"#splitline{Maximum}{Deviation}");
text.DrawClone();
mycanvas->Print("graph_with_law.pdf");
}
int main(){
macro1();
}Let’s comment it in detail:
Line 13: the name of the principal function (it plays the role of the “main” function in compiled programs) in the macro file. It has to be the same as the file name without extension.
Line 24-25: instance of the TGraphErrors class. The constructor takes the number of points and the pointers to the arrays of x values, y values, x errors (in this case none, represented by the NULL pointer) and y errors. The second line defines in one shot the title of the graph and the titles of the two axes, separated by a “;”.
Line 28-30: These three lines are rather intuitive right ? To understand better the enumerators for colours and styles see the reference for the TColor and TMarker classes.
Line 33: the canvas object that will host the drawn objects. The “memory leak” is intentional, to make the object existing also out of the macro1 scope.
Line 36: the method DrawClone draws a clone of the object on the canvas. It has to be a clone, to survive after the scope of macro1, and be displayed on screen after the end of the macro execution. The string option “APE” stands for:
A imposes the drawing of the Axes.
P imposes the drawing of the graph’s markers.
E imposes the drawing of the graph’s error bars.
Line 39: define a mathematical function. There are several ways to accomplish this, but in this case the constructor accepts the name of the function, the formula, and the function range.
Line 41: maquillage. Try to give a look to the line styles at your disposal visiting the documentation of the TLine class.
Line 43: fits the f function to the graph, observe that the pointer is passed. It is more interesting to look at the output on the screen to see the parameters values and other crucial information that we will learn to read at the end of this guide.
Line 44: again draws the clone of the object on the canvas. The “Same” option avoids the cancellation of the already drawn objects, in our case, the graph. The function f will be drawn using the same axis system defined by the previously drawn graph.
Line 47-52: completes the plot with a legend, represented by a TLegend instance. The constructor takes as parameters the lower left and upper right corners coordinates with respect to the total size of the canvas, assumed to be 1, and the legend header string. You can add to the legend the objects, previously drawn or not drawn, through the addEntry method. Observe how the legend is drawn at the end: looks familiar now, right ?
Line 55-57: defines an arrow with a triangle on the right hand side, a thickness of 2 and draws it.
Line 60-61: interpret a Latex string which hast its lower left corner located in the specified coordinate. The #splitline{}{} construct allows to store multiple lines in the same TLatex object.
Line 63: save the canvas as image. The format is automatically inferred from the file extension (it could have been eps, gif, …).
Let’s give a look to the obtained plot in Figure 3.1. Beautiful outcome for such a small bunch of lines, isn’t it ?
We have seen that to specify a colour, some identifiers like kWhite, kRed or kBlue can be specified for markers, lines, arrows etc. The complete summary of colours is represented by the ROOT “colour wheel”. To know more about the full story, refer to the online documentation of TColor.
ROOT provides several graphics markers types. Select the most suited symbols for your plot among dots, triangles, crosses or stars. An alternative set of names for the markers is available.
The macro line 55 shows how to define an arrow and draw it. The class representing arrows is TArrow, which inherits from TLine. The constructors of lines and arrows always contain the coordinates of the endpoints. Arrows also foresee parameters to specify their shapes. Do not underestimate the role of lines and arrows in your plots. Since each plot should contain a message, it is convenient to stress it with additional graphics primitives.
Also text plays a fundamental role in making the plots self-explanatory. A possibility to add text in your plot is provided by the TLatex class. The objects of this class are constructed with the coordinates of the bottom-left corner of the text and a string which contains the text itself. The real twist is that ordinary Latex mathematical symbols are automatically interpreted, you just need to replace the “\” by a “#”.
If “\” is used as control character , then the TMathText interface is invoked. It provides the plain TeX syntax and allow to access character’s set like Russian and Japanese.
As you observed, up to now we heavily exploited the capabilities of ROOT for interpreting our code, more than compiling and then executing. This is sufficient for a wide range of applications, but you might have already asked yourself “how can this code be compiled ?”. There are two answers.
ACLiC will create for you a compiled dynamic library for your macro, without any effort from your side, except the insertion of the appropriate header files in lines 5–11. In this example, they are already included. To generate an object library from the macro code, from inside the interpreter type (please note the “+”):
Once this operation is accomplished, the macro symbols will be available in memory and you will be able to execute it simply by calling from inside the interpreter:
A plethora of excellent compilers are available, both free and commercial. We will refer to the GCC compiler in the following. In this case, you have to include the appropriate headers in the code and then exploit the root-config tool for the automatic settings of all the compiler flags. root-config is a script that comes with ROOT; it prints all flags and libraries needed to compile code and link it with the ROOT libraries. In order to make the code executable stand-alone, an entry point for the operating system is needed, in C++ this is the procedure int main();. The easiest way to turn a ROOT macro code into a stand-alone application is to add the following “dressing code” at the end of the macro file. This defines the procedure main, the only purpose of which is to call your macro:
To create a stand-alone program from a macro called ExampleMacro.C, simply type
and execute it by typing
This procedure will, however, not give access to the ROOT graphics, as neither control of mouse or keyboard events nor access to the graphics windows of ROOT is available. If you want your stand-alone application have display graphics output and respond to mouse and keyboard, a slightly more complex piece of code can be used. In the example below, a macro ExampleMacro_GUI is executed by the ROOT class TApplication. As a additional feature, this code example offers access to parameters eventually passed to the program when started from the command line. Here is the code fragment:
void StandaloneApplication(int argc, char** argv) {
// eventually, evaluate the application parameters argc, argv
// ==>> here the ROOT macro is called
ExampleMacro_GUI();
}
// This is the standard "main" of C++ starting
// a ROOT application
int main(int argc, char** argv) {
TApplication app("ROOT Application", &argc, argv);
StandaloneApplication(app.Argc(), app.Argv());
app.Run();
return 0;
}Compile the code with
and execute the program with
In this Chapter we will learn how to exploit some of the functionalities ROOT provides to display data exploiting the class TGraphErrors, which you already got to know previously.
The fastest way in which you can fill a graph with experimental data is to use the constructor which reads data points and their errors from an ASCII file (i.e. standard text) format:
The format string can be:
"%lg %lg" read only 2 first columns into X,Y
"%lg %lg %lg" read only 3 first columns into X,Y and EY
"%lg %lg %lg %lg" read only 4 first columns into X,Y,EX,EY
This approach has the nice feature of allowing the user to reuse the macro for many different data sets. Here is an example of an input file. The nice graphic result shown is produced by the macro below, which reads two such input files and uses different options to display the data points.
# Measurement of Friday 26 March
# Experiment 2 Physics Lab
1 6 5
2 12 5
3 14 4.7
4 20 4.5
5 22 4.2
6 24 5.1
7 35 2.9
8 45 4.1
9 44 4.8
10 53 5.43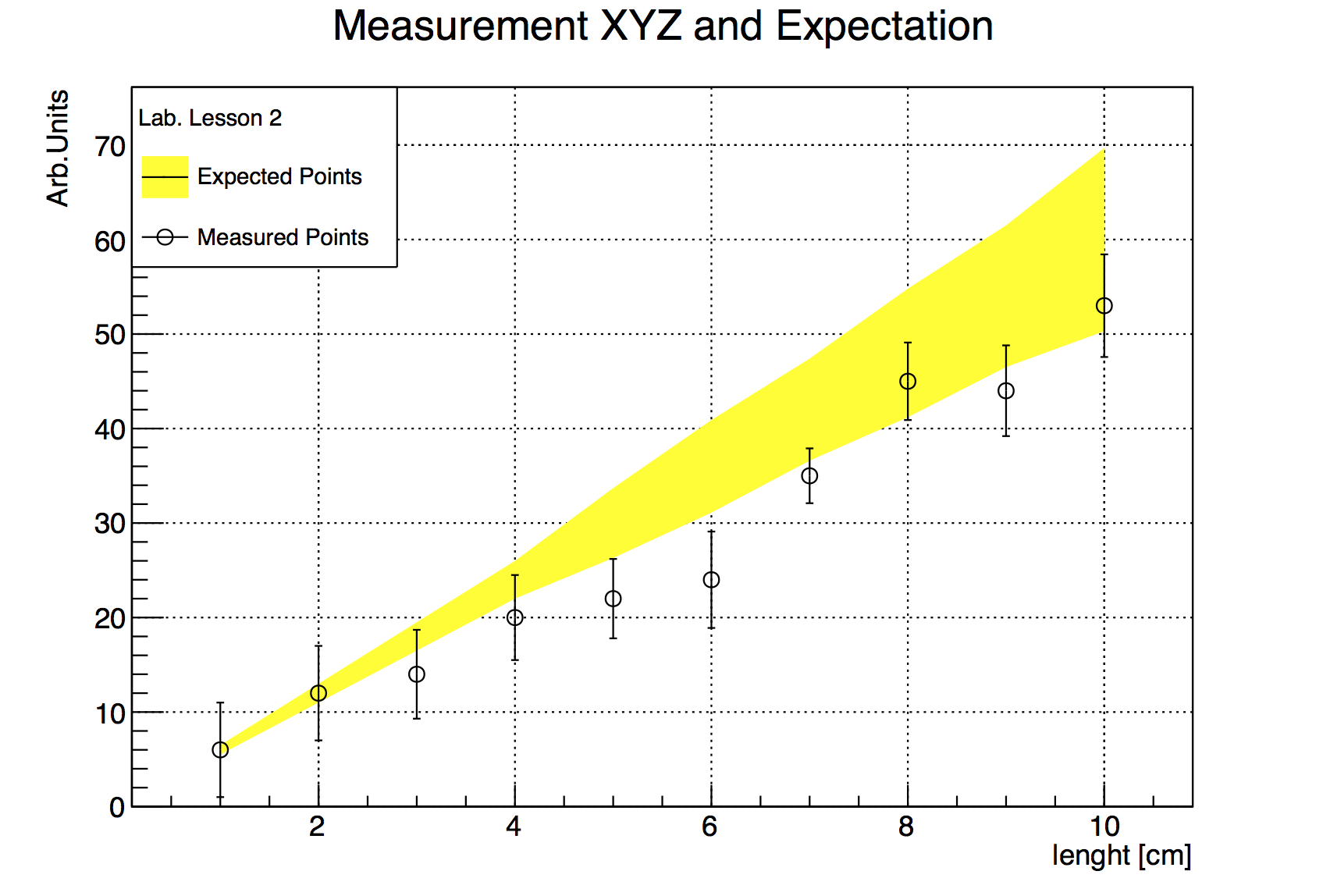
// Reads the points from a file and produces a simple graph.
int macro2(){
auto c=new TCanvas();c->SetGrid();
TGraphErrors graph_expected("./macro2_input_expected.txt",
"%lg %lg %lg");
graph_expected.SetTitle(
"Measurement XYZ and Expectation;"
"length [cm];"
"Arb.Units");
graph_expected.SetFillColor(kYellow);
graph_expected.DrawClone("E3AL"); // E3 draws the band
TGraphErrors graph("./macro2_input.txt","%lg %lg %lg");
graph.SetMarkerStyle(kCircle);
graph.SetFillColor(0);
graph.DrawClone("PESame");
// Draw the Legend
TLegend leg(.1,.7,.3,.9,"Lab. Lesson 2");
leg.SetFillColor(0);
leg.AddEntry(&graph_expected,"Expected Points");
leg.AddEntry(&graph,"Measured Points");
leg.DrawClone("Same");
graph.Print();
return 0;
}In addition to the inspection of the plot, you can check the actual contents of the graph with the TGraph::Print() method at any time, obtaining a printout of the coordinates of data points on screen. The macro also shows us how to print a coloured band around a graph instead of error bars, quite useful for example to represent the errors of a theoretical prediction.
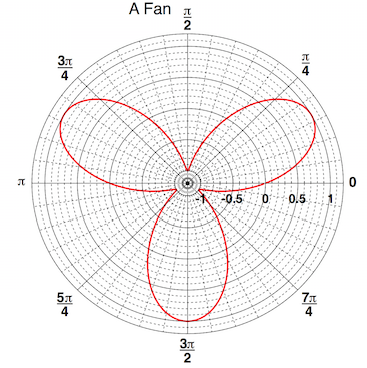
With ROOT you can profit from rather advanced plotting routines, like the ones implemented in the TPolarGraph, a class to draw graphs in polar coordinates. You can see the example macro in the following and the resulting Figure is 4.2:
// Builds a polar graph in a square Canvas.
void macro3(){
auto c = new TCanvas("myCanvas","myCanvas",600,600);
double rmin = 0.;
double rmax = TMath::Pi()*6.;
const int npoints = 1000;
double r[npoints];
double theta[npoints];
for (int ipt = 0; ipt < npoints; ipt++) {
theta[ipt] = ipt*(rmax-rmin)/npoints+rmin;
r[ipt] = TMath::Sin(theta[ipt]);
}
auto grP1 = new TGraphPolar(npoints,theta,r);
grP1->SetTitle("A Fan");
grP1->SetLineWidth(3);
grP1->SetLineColor(2);
grP1->Draw("L");
gPad->Update();
grP1->GetPolargram()->SetToRadian();
}A new element was added on line 4, the size of the canvas: it is sometimes optically better to show plots in specific canvas sizes.
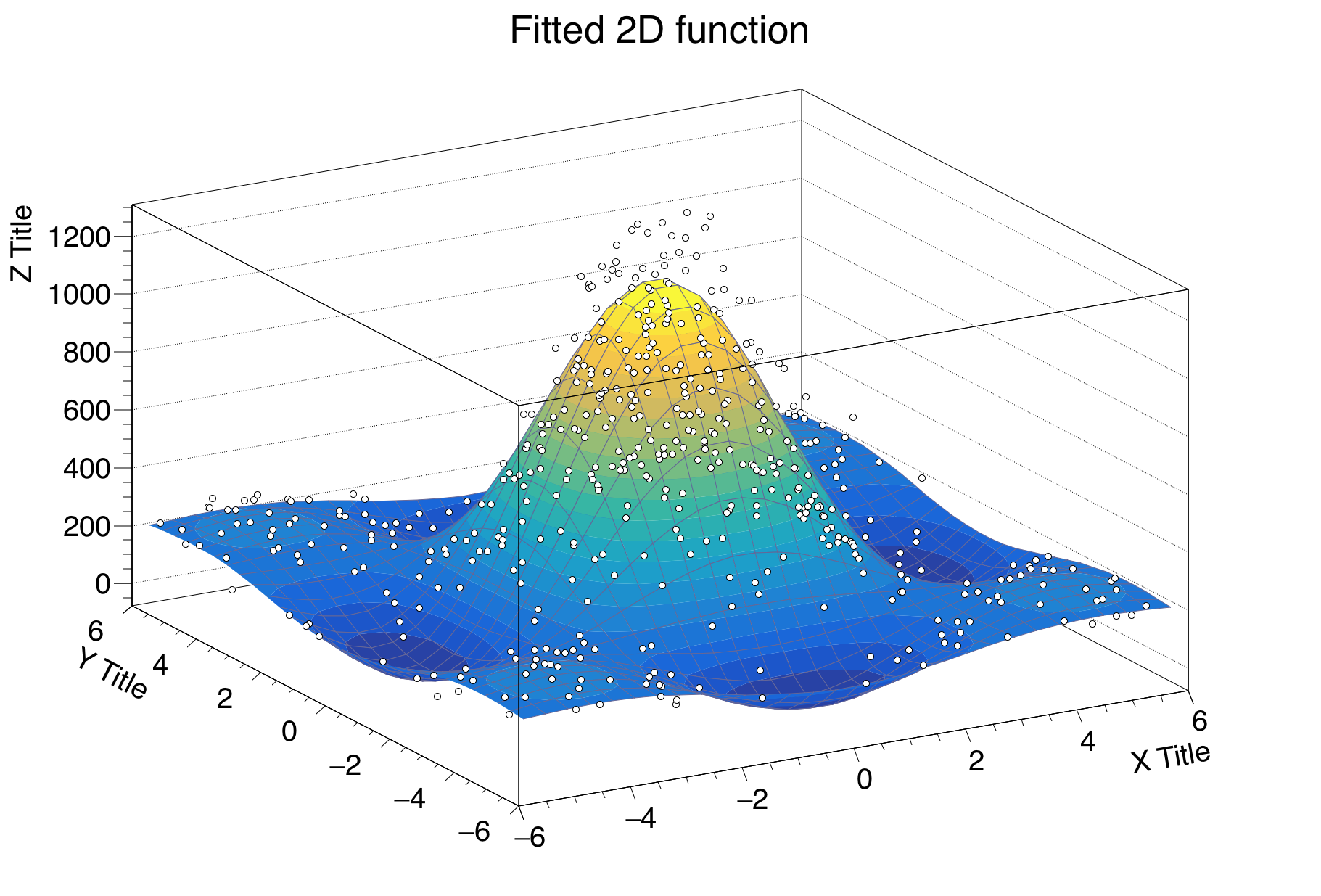
Under specific circumstances, it might be useful to plot some quantities versus two variables, therefore creating a bi-dimensional graph. Of course ROOT can help you in this task, with the TGraph2DErrors class. The following macro produces a bi-dimensional graph representing a hypothetical measurement, fits a bi-dimensional function to it and draws it together with its x and y projections. Some points of the code will be explained in detail. This time, the graph is populated with data points using random numbers, introducing a new and very important ingredient, the ROOT TRandom3 random number generator using the Mersenne Twister algorithm (Matsumoto 1997).
// Create, Draw and fit a TGraph2DErrors
void macro4(){
gStyle->SetPalette(kBird);
const double e = 0.3;
const int nd = 500;
TRandom3 my_random_generator;
TF2 f2("f2",
"1000*(([0]*sin(x)/x)*([1]*sin(y)/y))+200",
-6,6,-6,6);
f2.SetParameters(1,1);
TGraph2DErrors dte(nd);
// Fill the 2D graph
double rnd, x, y, z, ex, ey, ez;
for (Int_t i=0; i<nd; i++) {
f2.GetRandom2(x,y);
// A random number in [-e,e]
rnd = my_random_generator.Uniform(-e,e);
z = f2.Eval(x,y)*(1+rnd);
dte.SetPoint(i,x,y,z);
ex = 0.05*my_random_generator.Uniform();
ey = 0.05*my_random_generator.Uniform();
ez = fabs(z*rnd);
dte.SetPointError(i,ex,ey,ez);
}
// Fit function to generated data
f2.SetParameters(0.7,1.5); // set initial values for fit
f2.SetTitle("Fitted 2D function");
dte.Fit(&f2);
// Plot the result
auto c1 = new TCanvas();
f2.SetLineWidth(1);
f2.SetLineColor(kBlue-5);
TF2 *f2c = (TF2*)f2.DrawClone("Surf1");
TAxis *Xaxis = f2c->GetXaxis();
TAxis *Yaxis = f2c->GetYaxis();
TAxis *Zaxis = f2c->GetZaxis();
Xaxis->SetTitle("X Title"); Xaxis->SetTitleOffset(1.5);
Yaxis->SetTitle("Y Title"); Yaxis->SetTitleOffset(1.5);
Zaxis->SetTitle("Z Title"); Zaxis->SetTitleOffset(1.5);
dte.DrawClone("P0 Same");
// Make the x and y projections
auto c_p= new TCanvas("ProjCan",
"The Projections",1000,400);
c_p->Divide(2,1);
c_p->cd(1);
dte.Project("x")->Draw();
c_p->cd(2);
dte.Project("y")->Draw();
}Let’s go through the code, step by step to understand what is going on:
Line 3: This sets the palette colour code to a much nicer one than the default. Comment this line to give it a try. This article gives more details about colour map choice.
Line 7: The instance of the random generator. You can then draw out of this instance random numbers distributed according to different probability density functions, like the Uniform one at lines 27-29. See the on-line documentation to appreciate the full power of this ROOT feature.
Line 8: You are already familiar with the TF1 class. This is its two-dimensional version. At line 16 two random numbers distributed according to the TF2 formula are drawn with the method TF2::GetRandom2(double& a, double&b).
Line 27-29: Fitting a 2-dimensional function just works like in the one-dimensional case, i.e. initialisation of parameters and calling of the Fit() method.
Line 34: The Surf1 option draws the TF2 objects (but also bi-dimensional histograms) as coloured surfaces with a wire-frame on three-dimensional canvases. See Figure 4.3.
Line 35-40: Retrieve the axis pointer and define the axis titles.
Line 41: Draw the cloud of points on top of the coloured surface.
Line 43-49: Here you learn how to create a canvas, partition it in two sub-pads and access them. It is very handy to show multiple plots in the same window or image.
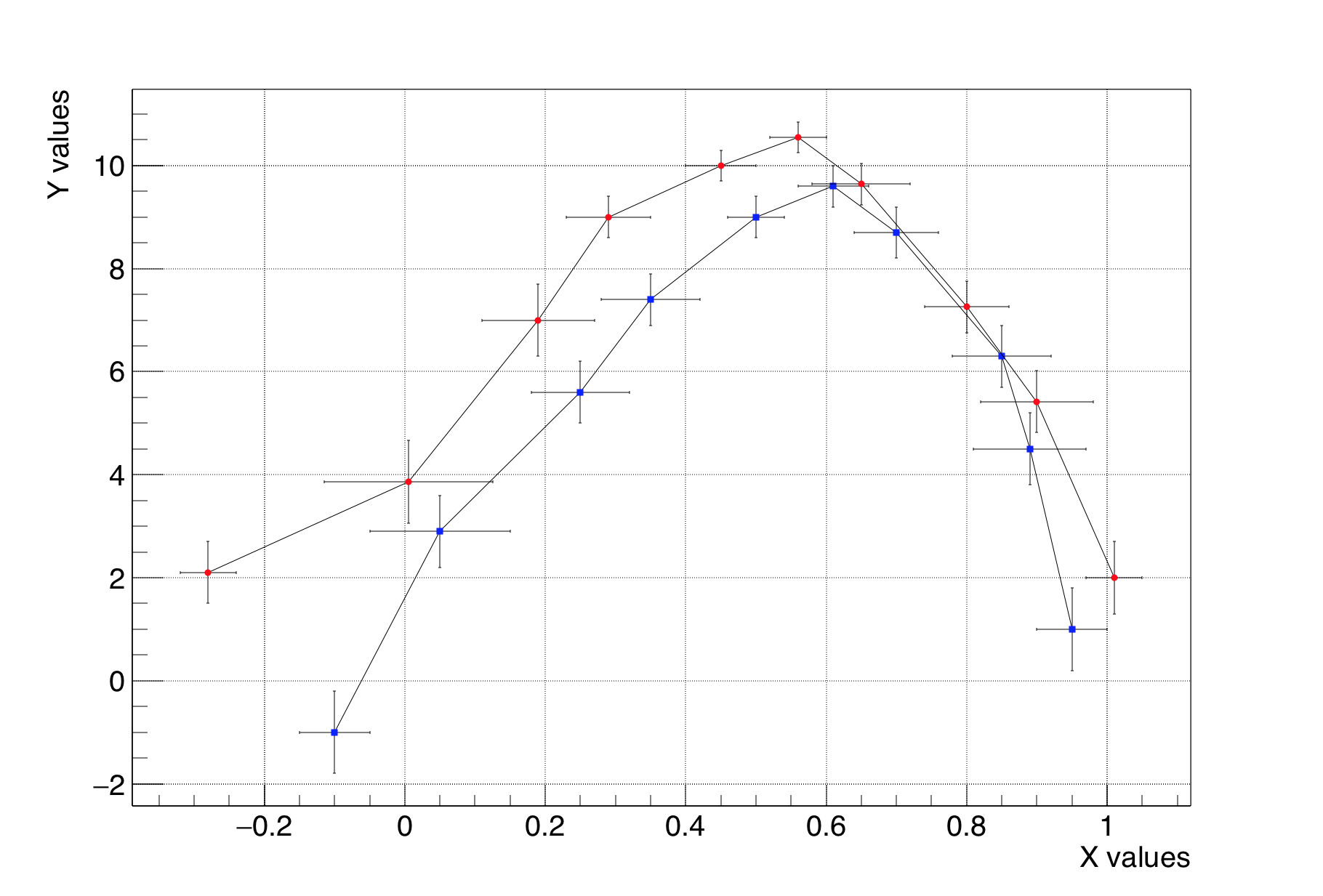
The class TMultigraph allows to manipulate a set of graphs as a single entity. It is a collection of TGraph (or derived) objects. When drawn, the X and Y axis ranges are automatically computed such as all the graphs will be visible.
// Manage several graphs as a single entity.
void multigraph(){
TCanvas *c1 = new TCanvas("c1","multigraph",700,500);
c1->SetGrid();
TMultiGraph *mg = new TMultiGraph();
// create first graph
const Int_t n1 = 10;
Double_t px1[] = {-0.1, 0.05, 0.25, 0.35, 0.5, 0.61,0.7,0.85,0.89,0.95};
Double_t py1[] = {-1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
Double_t ex1[] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
Double_t ey1[] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
TGraphErrors *gr1 = new TGraphErrors(n1,px1,py1,ex1,ey1);
gr1->SetMarkerColor(kBlue);
gr1->SetMarkerStyle(21);
mg->Add(gr1);
// create second graph
const Int_t n2 = 10;
Float_t x2[] = {-0.28, 0.005, 0.19, 0.29, 0.45, 0.56,0.65,0.80,0.90,1.01};
Float_t y2[] = {2.1,3.86,7,9,10,10.55,9.64,7.26,5.42,2};
Float_t ex2[] = {.04,.12,.08,.06,.05,.04,.07,.06,.08,.04};
Float_t ey2[] = {.6,.8,.7,.4,.3,.3,.4,.5,.6,.7};
TGraphErrors *gr2 = new TGraphErrors(n2,x2,y2,ex2,ey2);
gr2->SetMarkerColor(kRed);
gr2->SetMarkerStyle(20);
mg->Add(gr2);
mg->Draw("apl");
mg->GetXaxis()->SetTitle("X values");
mg->GetYaxis()->SetTitle("Y values");
gPad->Update();
gPad->Modified();
}Line 6 creates the multigraph.
Line 9-28: create two graphs with errors and add them in the multigraph.
Line 30-32: draw the multigraph. The axis limits are computed automatically to make sure all the graphs’ points will be in range.
[^3] https://root.cern/blog/rainbow-color-map/
Histograms play a fundamental role in any type of physics analysis, not only to visualise measurements but being a powerful form of data reduction. ROOT offers many classes that represent histograms, all inheriting from the TH1 class. We will focus in this chapter on uni- and bi- dimensional histograms the bin contents of which are represented by floating point numbers,2 the TH1F and TH2F classes respectively.
Let’s suppose you want to measure the counts of a Geiger detector located in proximity of a radioactive source in a given time interval. This would give you an idea of the activity of your source. The count distribution in this case is a Poisson distribution. Let’s see how operatively you can fill and draw a histogram with the following example macro.
// Create, Fill and draw an Histogram which reproduces the
// counts of a scaler linked to a Geiger counter.
void macro5(){
auto cnt_r_h=new TH1F("count_rate",
"Count Rate;N_{Counts};# occurencies",
100, // Number of Bins
-0.5, // Lower X Boundary
15.5); // Upper X Boundary
auto mean_count=3.6f;
TRandom3 rndgen;
// simulate the measurements
for (int imeas=0;imeas<400;imeas++)
cnt_r_h->Fill(rndgen.Poisson(mean_count));
auto c= new TCanvas();
cnt_r_h->Draw();
auto c_norm= new TCanvas();
cnt_r_h->DrawNormalized();
// Print summary
cout << "Moments of Distribution:\n"
<< " - Mean = " << cnt_r_h->GetMean() << " +- "
<< cnt_r_h->GetMeanError() << "\n"
<< " - Std Dev = " << cnt_r_h->GetStdDev() << " +- "
<< cnt_r_h->GetStdDevError() << "\n"
<< " - Skewness = " << cnt_r_h->GetSkewness() << "\n"
<< " - Kurtosis = " << cnt_r_h->GetKurtosis() << "\n";
}Which gives you the following plot (Figure 5.1):
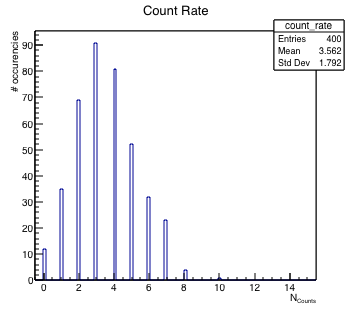
Using histograms is rather simple. The main differences with respect to graphs that emerge from the example are:
line 5: The histograms have a name and a title right from the start, no predefined number of entries but a number of bins and a lower-upper range.
line 15: An entry is stored in the histogram through the TH1F::Fill method.
line 18 and 21: The histogram can be drawn also normalised, ROOT automatically takes cares of the necessary rescaling.
line 24 to 30: This small snippet shows how easy it is to access the moments and associated errors of a histogram.
Quite a large number of operations can be carried out with histograms. The most useful are addition and division. In the following macro we will learn how to manage these procedures within ROOT.
// Divide and add 1D Histograms
void format_h(TH1F* h, int linecolor){
h->SetLineWidth(3);
h->SetLineColor(linecolor);
}
void macro6(){
auto sig_h=new TH1F("sig_h","Signal Histo",50,0,10);
auto gaus_h1=new TH1F("gaus_h1","Gauss Histo 1",30,0,10);
auto gaus_h2=new TH1F("gaus_h2","Gauss Histo 2",30,0,10);
auto bkg_h=new TH1F("exp_h","Exponential Histo",50,0,10);
// simulate the measurements
TRandom3 rndgen;
for (int imeas=0;imeas<4000;imeas++){
bkg_h->Fill(rndgen.Exp(4));
if (imeas%4==0) gaus_h1->Fill(rndgen.Gaus(5,2));
if (imeas%4==0) gaus_h2->Fill(rndgen.Gaus(5,2));
if (imeas%10==0)sig_h->Fill(rndgen.Gaus(5,.5));}
// Format Histograms
int i=0;
for (auto hist : {sig_h,bkg_h,gaus_h1,gaus_h2})
format_h(hist,1+i++);
// Sum
auto sum_h= new TH1F(*bkg_h);
sum_h->Add(sig_h,1.);
sum_h->SetTitle("Exponential + Gaussian;X variable;Y variable");
format_h(sum_h,kBlue);
auto c_sum= new TCanvas();
sum_h->Draw("hist");
bkg_h->Draw("SameHist");
sig_h->Draw("SameHist");
// Divide
auto dividend=new TH1F(*gaus_h1);
dividend->Divide(gaus_h2);
// Graphical Maquillage
dividend->SetTitle(";X axis;Gaus Histo 1 / Gaus Histo 2");
format_h(dividend,kOrange);
gaus_h1->SetTitle(";;Gaus Histo 1 and Gaus Histo 2");
gStyle->SetOptStat(0);
TCanvas* c_divide= new TCanvas();
c_divide->Divide(1,2,0,0);
c_divide->cd(1);
c_divide->GetPad(1)->SetRightMargin(.01);
gaus_h1->DrawNormalized("Hist");
gaus_h2->DrawNormalized("HistSame");
c_divide->cd(2);
dividend->GetYaxis()->SetRangeUser(0,2.49);
c_divide->GetPad(2)->SetGridy();
c_divide->GetPad(2)->SetRightMargin(.01);
dividend->Draw();
}The plots that you will obtain are shown in Figures 5.2 and 5.3.
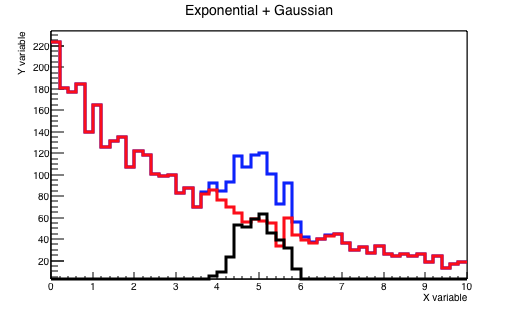
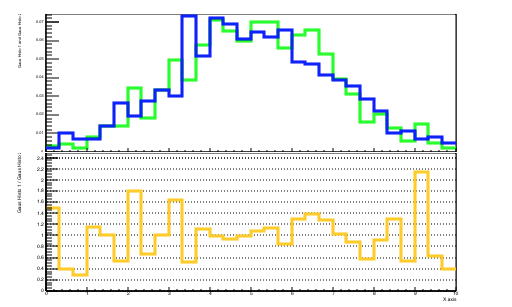
Some lines now need a bit of clarification:
line 3: Cling, as we know, is also able to interpret more than one function per file. In this case the function simply sets up some parameters to conveniently set the line of histograms.
line 19 to 21: Some C++ syntax for conditional statements is used to fill the histograms with different numbers of entries inside the loop.
line 30: The sum of two histograms. A weight, which can be negative, can be assigned to the added histogram.
line 41: The division of two histograms is rather straightforward.
line 44 to 62: When you draw two quantities and their ratios, it is much better if all the information is condensed in one single plot. These lines provide a skeleton to perform this operation.
Two-dimensional histograms are a very useful tool, for example to inspect correlations between variables. You can exploit the bi-dimensional histogram classes provided by ROOT in a simple way. Let’s see how in this macro:
// Draw a Bidimensional Histogram in many ways
// together with its profiles and projections
void macro7(){
gStyle->SetPalette(kBird);
gStyle->SetOptStat(0);
gStyle->SetOptTitle(0);
auto bidi_h = new TH2F("bidi_h","2D Histo;Gaussian Vals;Exp. Vals",
30,-5,5, // X axis
30,0,10); // Y axis
TRandom3 rgen;
for (int i=0;i<500000;i++) {
bidi_h->Fill(rgen.Gaus(0,2),10-rgen.Exp(4),.1);
}
auto c=new TCanvas("Canvas","Canvas",800,800);
c->Divide(2,2);
c->cd(1); bidi_h->Draw("Cont1");
c->cd(2); bidi_h->Draw("Colz");
c->cd(3); bidi_h->Draw("Lego2");
c->cd(4); bidi_h->Draw("Surf3");
// Profiles and Projections
auto c2=new TCanvas("Canvas2","Canvas2",800,800);
c2->Divide(2,2);
c2->cd(1); bidi_h->ProjectionX()->Draw();
c2->cd(2); bidi_h->ProjectionY()->Draw();
c2->cd(3); bidi_h->ProfileX()->Draw();
c2->cd(4); bidi_h->ProfileY()->Draw();
}Two kinds of plots are provided within the code, the first one containing three-dimensional representations (Figure 5.4) and the second one projections and profiles (Figure 5.5) of the bi-dimensional histogram.
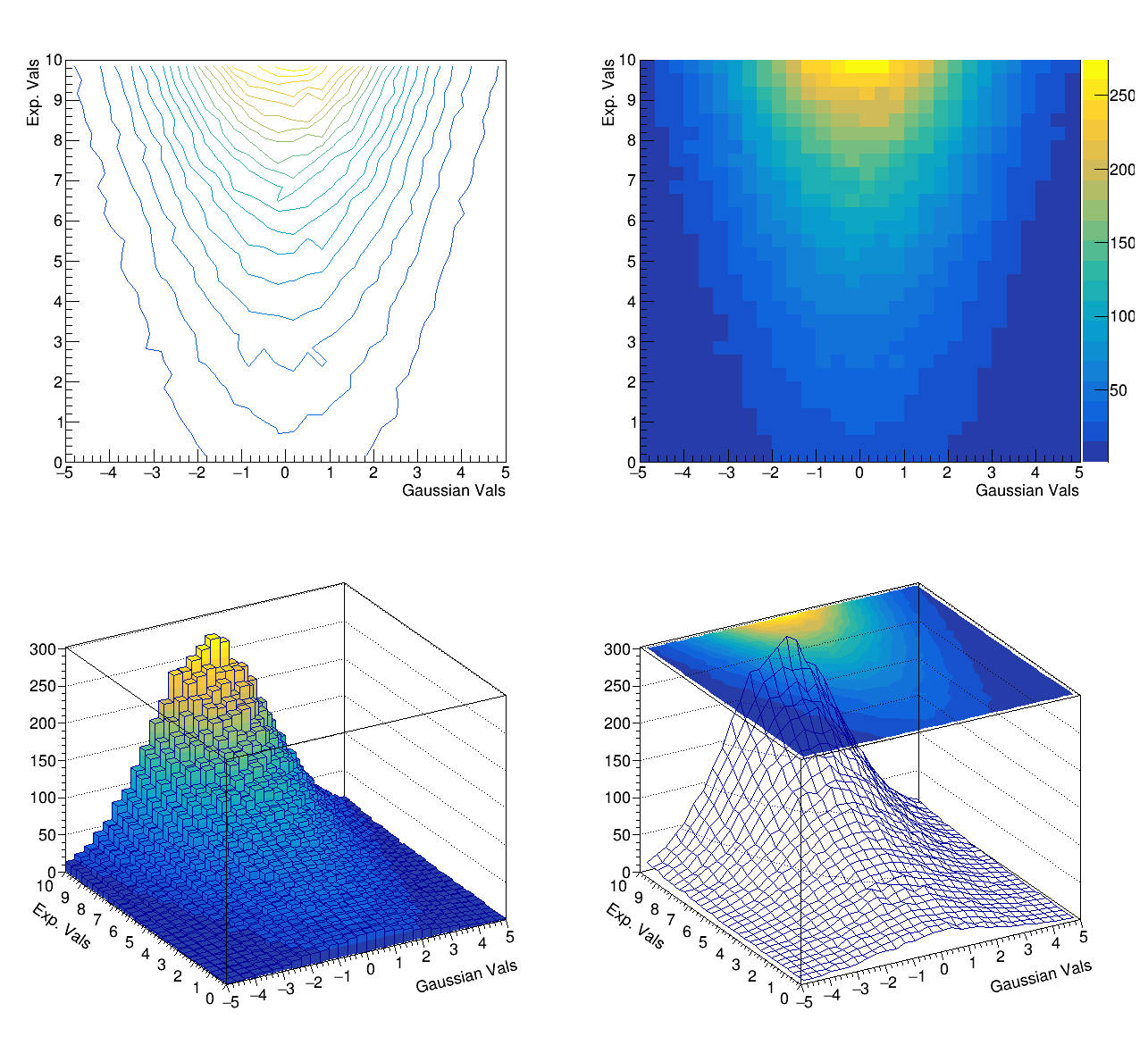
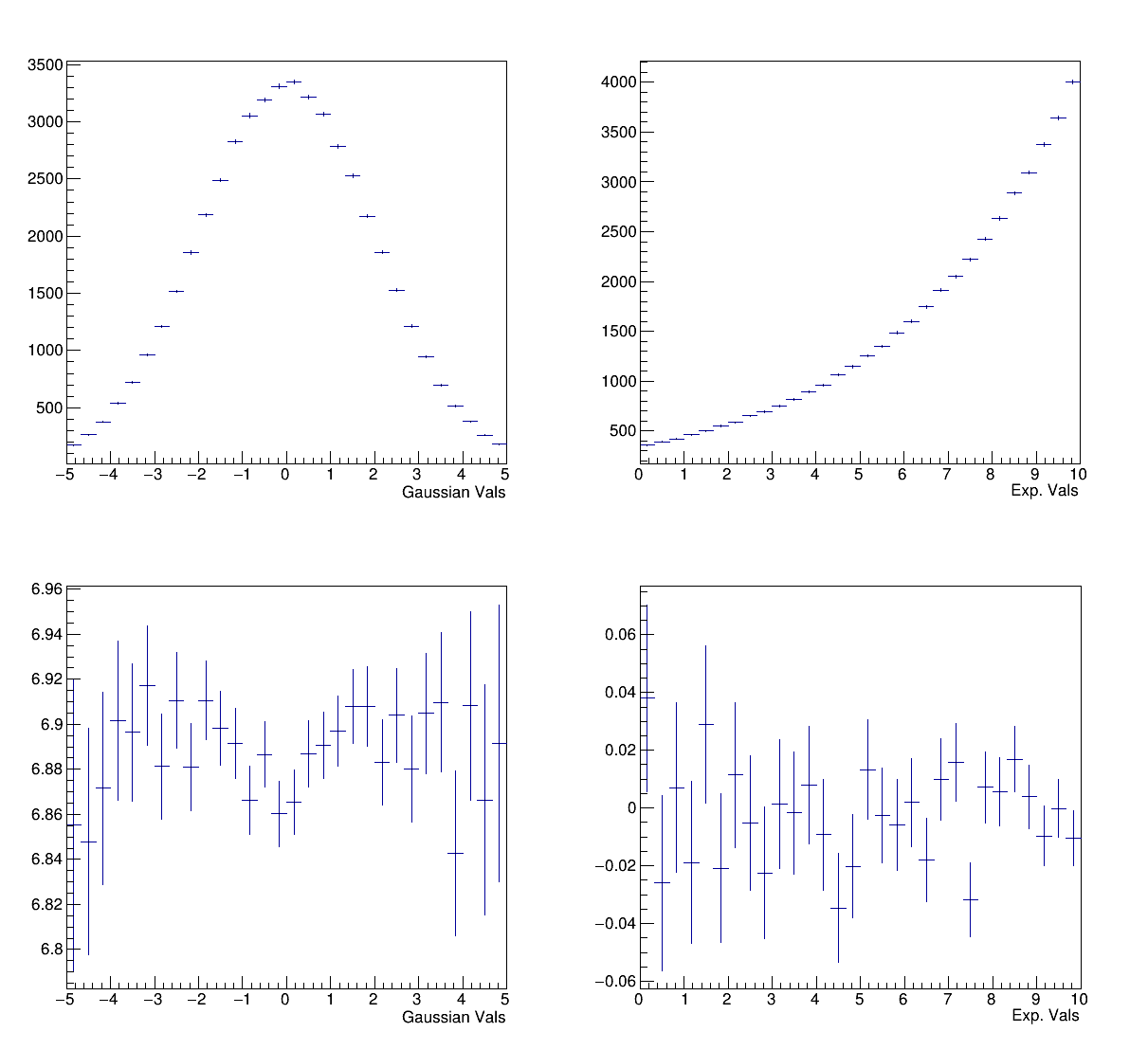
When a projection is performed along the x (y) direction, for every bin along the x (y) axis, all bin contents along the y (x) axis are summed up (upper the plots of Figure 5.5). When a profile is performed along the x (y) direction, for every bin along the x (y) axis, the average of all the bin contents along the y (x) is calculated together with their RMS and displayed as a symbol with error bar (lower two plots of Figure 5.5).
Correlations between the variables are quantified by the methods Double_t GetCovariance() and Double_t GetCorrelationFactor().
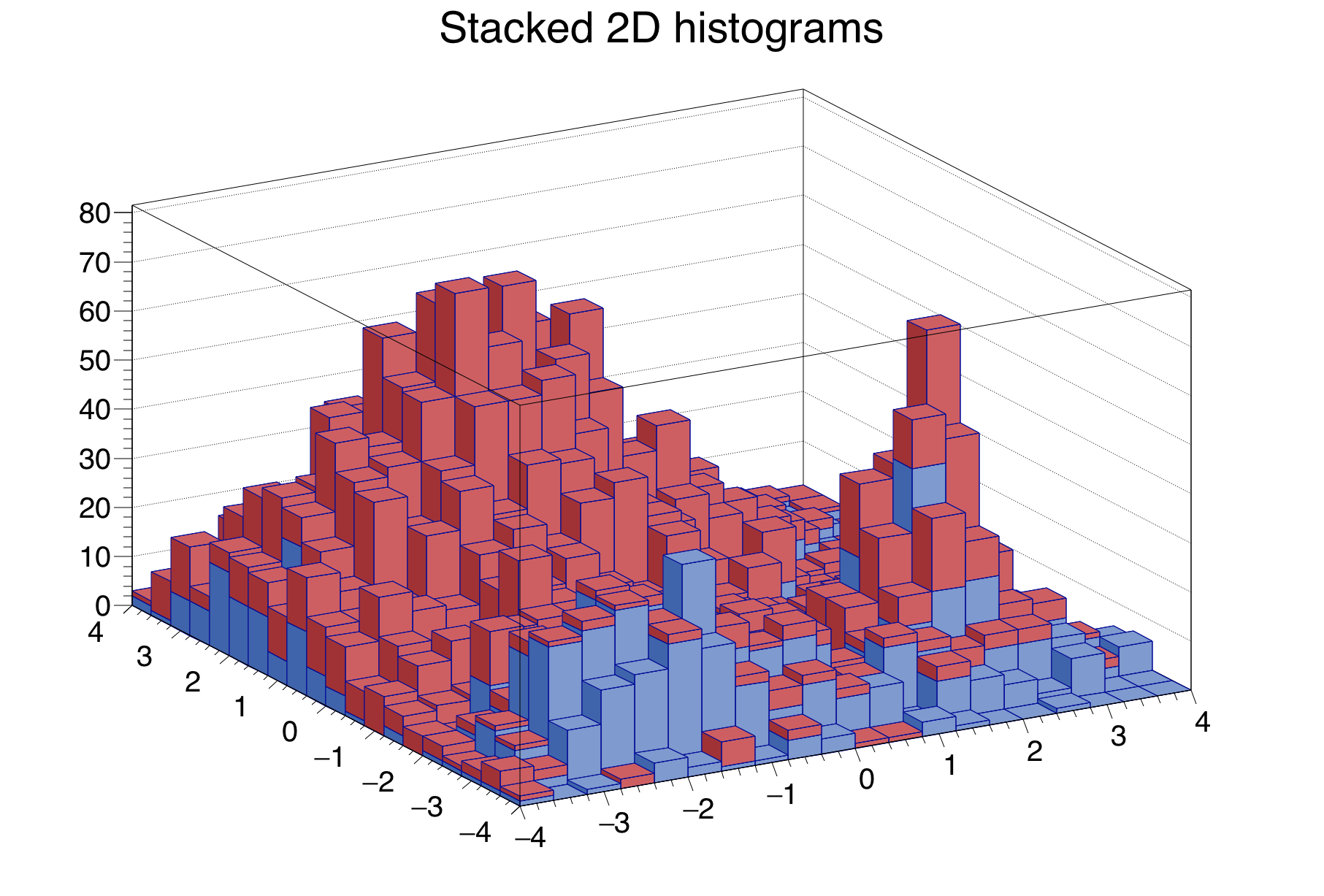
The class THStack allows to manipulate a set of histograms as a single entity. It is a collection of TH1 (or derived) objects. When drawn, the X and Y axis ranges are automatically computed such as all the histograms will be visible. Several drawing option are available for both 1D and 2D histograms. The next macros shows how it looks for 2D histograms:
// Example of stacked histograms using the class THStack
void hstack(){
THStack *a = new THStack("a","Stacked 2D histograms");
TF2 *f1 = new TF2("f1","xygaus + xygaus(5) + xylandau(10)",-4,4,-4,4);
Double_t params1[] = {130,-1.4,1.8,1.5,1, 150,2,0.5,-2,0.5, 3600,-2,0.7,-3,0.3};
f1->SetParameters(params1);
TH2F *h2sta = new TH2F("h2sta","h2sta",20,-4,4,20,-4,4);
h2sta->SetFillColor(38);
h2sta->FillRandom("f1",4000);
TF2 *f2 = new TF2("f2","xygaus + xygaus(5)",-4,4,-4,4);
Double_t params2[] = {100,-1.4,1.9,1.1,2, 80,2,0.7,-2,0.5};
f2->SetParameters(params2);
TH2F *h2stb = new TH2F("h2stb","h2stb",20,-4,4,20,-4,4);
h2stb->SetFillColor(46);
h2stb->FillRandom("f2",3000);
a->Add(h2sta);
a->Add(h2stb);
a->Draw();
}Line 4: creates the stack.
Lines 4-18: create two histograms to be added in the stack.
Lines 20-21: add the histograms in the stack.
Line 23: draws the stack as a lego plot. The colour distinguish the two histograms 5.6.
After going through the previous chapters, you already know how to use analytical functions (class TF1), and you got some insight into the graph (TGraphErrors) and histogram classes (TH1F) for data visualisation. In this chapter we will add more detail to the previous approximate explanations to face the fundamental topic of parameter estimation by fitting functions to data. For graphs and histograms, ROOT offers an easy-to-use interface to perform fits - either the fit panel of the graphical interface, or the Fit method. The class TFitResult allows access to the detailed results.
Very often it is necessary to study the statistical properties of analysis procedures. This is most easily achieved by applying the analysis to many sets of simulated data (or “pseudo data”), each representing one possible version of the true experiment. If the simulation only deals with the final distributions observed in data, and does not perform a full simulation of the underlying physics and the experimental apparatus, the name “Toy Monte Carlo” is frequently used.3 Since the true values of all parameters are known in the pseudo-data, the differences between the parameter estimates from the analysis procedure w.r.t. the true values can be determined, and it is also possible to check that the analysis procedure provides correct error estimates.
In the example below, a pseudo-data set is produced and a model fitted to it.
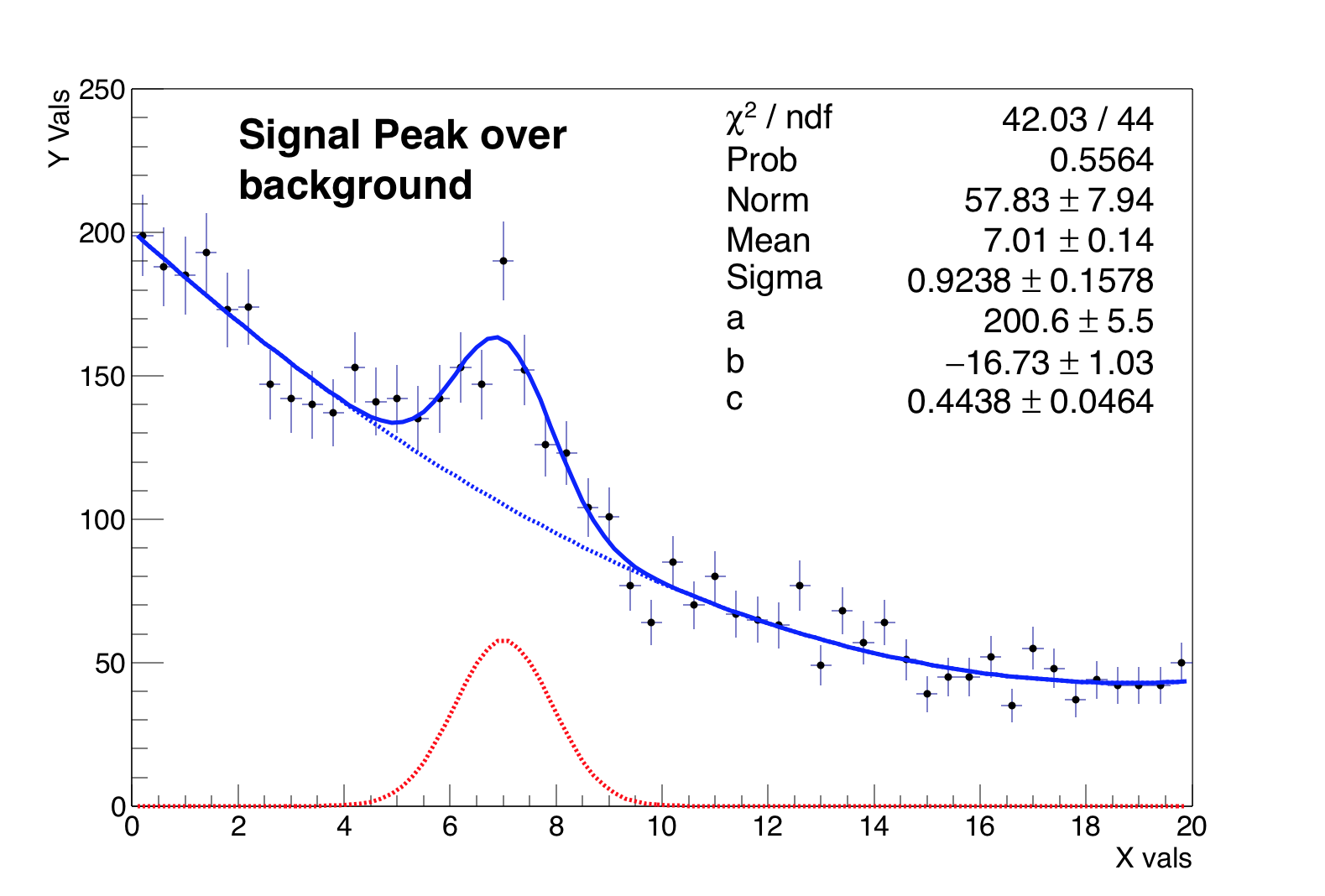
ROOT offers various minimisation algorithms to minimise a chi2 or a negative log-likelihood function. The default minimiser is MINUIT, a package originally implemented in the FORTRAN programming language. A C++ version is also available, MINUIT2, as well as Fumili (Silin 1983) an algorithm optimised for fitting. The minimisation algorithms can be selected using the static functions of the ROOT::Math::MinimizerOptions class. Steering options for the minimiser, such as the convergence tolerance or the maximum number of function calls, can also be set using the methods of this class. All currently implemented minimisers are documented in the reference documentation of ROOT: have a look for example to the ROOT::Math::Minimizer class documentation. The complication level of the code below is intentionally a little higher than in the previous examples. The graphical output of the macro is shown in Figure 6.1:
void format_line(TAttLine* line,int col,int sty){
line->SetLineWidth(5); line->SetLineColor(col);
line->SetLineStyle(sty);}
double the_gausppar(double* vars, double* pars){
return pars[0]*TMath::Gaus(vars[0],pars[1],pars[2])+
pars[3]+pars[4]*vars[0]+pars[5]*vars[0]*vars[0];}
int macro8(){
gStyle->SetOptTitle(0); gStyle->SetOptStat(0);
gStyle->SetOptFit(1111); gStyle->SetStatBorderSize(0);
gStyle->SetStatX(.89); gStyle->SetStatY(.89);
TF1 parabola("parabola","[0]+[1]*x+[2]*x**2",0,20);
format_line(¶bola,kBlue,2);
TF1 gaussian("gaussian","[0]*TMath::Gaus(x,[1],[2])",0,20);
format_line(&gaussian,kRed,2);
TF1 gausppar("gausppar",the_gausppar,-0,20,6);
double a=15; double b=-1.2; double c=.03;
double norm=4; double mean=7; double sigma=1;
gausppar.SetParameters(norm,mean,sigma,a,b,c);
gausppar.SetParNames("Norm","Mean","Sigma","a","b","c");
format_line(&gausppar,kBlue,1);
TH1F histo("histo","Signal plus background;X vals;Y Vals",50,0,20);
histo.SetMarkerStyle(8);
// Fake the data
for (int i=1;i<=5000;++i) histo.Fill(gausppar.GetRandom());
// Reset the parameters before the fit and set
// by eye a peak at 6 with an area of more or less 50
gausppar.SetParameter(0,50);
gausppar.SetParameter(1,6);
int npar=gausppar.GetNpar();
for (int ipar=2;ipar<npar;++ipar) gausppar.SetParameter(ipar,1);
// perform fit ...
auto fitResPtr = histo.Fit(&gausppar, "S");
// ... and retrieve fit results
fitResPtr->Print(); // print fit results
// get covariance Matrix an print it
TMatrixDSym covMatrix (fitResPtr->GetCovarianceMatrix());
covMatrix.Print();
// Set the values of the gaussian and parabola
for (int ipar=0;ipar<3;ipar++){
gaussian.SetParameter(ipar,gausppar.GetParameter(ipar));
parabola.SetParameter(ipar,gausppar.GetParameter(ipar+3));
}
histo.GetYaxis()->SetRangeUser(0,250);
histo.DrawClone("PE");
parabola.DrawClone("Same"); gaussian.DrawClone("Same");
TLatex latex(2,220,"#splitline{Signal Peak over}{background}");
latex.DrawClone("Same");
return 0;
}Some step by step explanation is at this point necessary:
Lines 1-3: A simple function to ease the make-up of lines. Remember that the class TF1 inherits from TAttLine.
Lines 5-7 : Definition of a customised function, namely a Gaussian (the “signal”) plus a parabolic function, the “background”.
Lines 10-12: Some make-up for the Canvas. In particular we want that the parameters of the fit appear very clearly and nicely on the plot.
Lines 20-25: Define and initialise an instance of TF1.
Lines 27-31: Define and fill a histogram.
Lines 33-38: For convenience, the same function as for the generation of the pseudo-data is used in the fit; hence, we need to reset the function parameters. This part of the code is very important for each fit procedure, as it sets the initial values of the fit.
Line 41: A very simple command, well known by now: fit the function to the histogram.
Lines 42-46: Retrieve the output from the fit. Here, we simply print the fit result and access and print the covariance matrix of the parameters.
Lines 54-end: Plot the pseudo-data, the fitted function and the signal and background components at the best-fit values.
Let us look at a simple example of a toy experiment comparing two methods to fit a function to a histogram, the \(\chi^{2}\)
method and a method called “binned log-likelihood fit”, both available in ROOT.
As a very simple yet powerful quantity to check the quality of the fit results, we construct for each pseudo-data set the so-called “pull”, the difference of the estimated and the true value of a parameter, normalised to the estimated error on the parameter, \(\frac{(p_{estim} - p_{true})}{\sigma_{p}}\). If everything is OK, the distribution of the pull values is a standard normal distribution, i.e. a Gaussian distribution centred around zero with a standard deviation of one.
The macro performs a rather big number of toy experiments, where a histogram is repeatedly filled with Gaussian distributed numbers, representing the pseudo-data in this example. Each time, a fit is performed according to the selected method, and the pull is calculated and filled into a histogram. Here is the code:
// Toy Monte Carlo example.
// Check pull distribution to compare chi2 and binned
// log-likelihood methods.
void pull( int n_toys = 10000,
int n_tot_entries = 100,
int nbins = 40,
bool do_chi2=true ){
TString method_prefix("Log-Likelihood ");
if (do_chi2)
method_prefix="#chi^{2} ";
// Create histo
TH1F h4(method_prefix+"h4",
method_prefix+" Random Gauss",
nbins,-4,4);
h4.SetMarkerStyle(21);
h4.SetMarkerSize(0.8);
h4.SetMarkerColor(kRed);
// Histogram for sigma and pull
TH1F sigma(method_prefix+"sigma",
method_prefix+"sigma from gaus fit",
50,0.5,1.5);
TH1F pull(method_prefix+"pull",
method_prefix+"pull from gaus fit",
50,-4.,4.);
// Make nice canvases
auto c0 = new TCanvas(method_prefix+"Gauss",
method_prefix+"Gauss",0,0,320,240);
c0->SetGrid();
// Make nice canvases
auto c1 = new TCanvas(method_prefix+"Result",
method_prefix+"Sigma-Distribution",
0,300,600,400);
c0->cd();
float sig, mean;
for (int i=0; i<n_toys; i++){
// Reset histo contents
h4.Reset();
// Fill histo
for ( int j = 0; j<n_tot_entries; j++ )
h4.Fill(gRandom->Gaus());
// perform fit
if (do_chi2) h4.Fit("gaus","q"); // Chi2 fit
else h4.Fit("gaus","lq"); // Likelihood fit
// some control output on the way
if (!(i%100)){
h4.Draw("ep");
c0->Update();}
// Get sigma from fit
TF1 *fit = h4.GetFunction("gaus");
sig = fit->GetParameter(2);
mean= fit->GetParameter(1);
sigma.Fill(sig);
pull.Fill(mean/sig * sqrt(n_tot_entries));
} // end of toy MC loop
// print result
c1->cd();
pull.DrawClone();
}
void macro9(){
int n_toys=10000;
int n_tot_entries=100;
int n_bins=40;
cout << "Performing Pull Experiment with chi2 \n";
pull(n_toys,n_tot_entries,n_bins,true);
cout << "Performing Pull Experiment with Log Likelihood\n";
pull(n_toys,n_tot_entries,n_bins,false);
}Your present knowledge of ROOT should be enough to understand all the technicalities behind the macro. Note that the variable pull in line 61 is different from the definition above: instead of the parameter error on mean, the fitted standard deviation of the distribution divided by the square root of the number of entries, sig/sqrt(n_tot_entries), is used.
What method exhibits the better performance with the default parameters ?
What happens if you increase the number of entries per histogram by a factor of ten ? Why ?
The answers to these questions are well beyond the scope of this guide. Basically all books about statistical methods provide a complete treatment of the aforementioned topics.
ROOT offers the possibility to write instances of classes on disk, into a ROOT-file (see the TFile class for more details). One says that the object is made “persistent” by storing it on disk. When reading the file back, the object is reconstructed in memory. The requirement to be satisfied to perform I/O of instances of a certain class is that the ROOT type system is aware of the layout in memory of that class. This topic is beyond the scope of this document: it is worth to mention that I/O can be performed out of the box for the almost complete set of ROOT classes.
We can explore this functionality with histograms and two simple macros.
void write_to_file(){
// Instance of our histogram
TH1F h("my_histogram","My Title;X;# of entries",100,-5,5);
// Let's fill it randomly
h.FillRandom("gaus");
// Let's open a TFile
TFile out_file("my_rootfile.root","RECREATE");
// Write the histogram in the file
h.Write();
// Close the file
out_file.Close();
}Not bad, eh ? Especially for a language that does not foresees persistency natively like C++. The RECREATE option forces ROOT to create a new file even if a file with the same name exists on disk.
Now, you may use the Cling command line to access information in the file and draw the previously written histogram:
> root my_rootfile.root
root [0]
Attaching file my_rootfile.root as _file0...
root [1] _file0->ls()
TFile** my_rootfile.root
TFile* my_rootfile.root
KEY: TH1F my_histogram;1 My Title
root [2] my_histogram->Draw()Alternatively, you can use a simple macro to carry out the job:
void read_from_file(){
// Let's open the TFile
TFile in_file("my_rootfile.root");
// Get the Histogram out
TH1F* h;
in_file.GetObject("my_histogram",h);
// Draw it
auto myCanvas = new TCanvas();
h->DrawClone();
}Up to now we have seen how to manipulate input read from ASCII files. ROOT offers the possibility to do much better than that, with its own n-tuple classes. Among the many advantages provided by these classes one could cite
Optimised disk I/O.
Possibility to store many n-tuple rows.
Write the n-tuples in ROOT files.
Interactive inspection with TBrowser.
Store not only numbers, but also objects in the columns.
In this section we will discuss briefly the TNtuple class, which is a simplified version of the TTree class. A ROOT TNtuple object can store rows of float entries. Let’s tackle the problem according to the usual strategy commenting a minimal example
// Fill an n-tuple and write it to a file simulating measurement of
// conductivity of a material in different conditions of pressure
// and temperature.
void write_ntuple_to_file(){
TFile ofile("conductivity_experiment.root","RECREATE");
// Initialise the TNtuple
TNtuple cond_data("cond_data",
"Example N-Tuple",
"Potential:Current:Temperature:Pressure");
// Fill it randomly to fake the acquired data
TRandom3 rndm;
float pot,cur,temp,pres;
for (int i=0;i<10000;++i){
pot=rndm.Uniform(0.,10.); // get voltage
temp=rndm.Uniform(250.,350.); // get temperature
pres=rndm.Uniform(0.5,1.5); // get pressure
cur=pot/(10.+0.05*(temp-300.)-0.2*(pres-1.)); // current
// add some random smearing (measurement errors)
pot*=rndm.Gaus(1.,0.01); // 1% error on voltage
temp+=rndm.Gaus(0.,0.3); // 0.3 abs. error on temp.
pres*=rndm.Gaus(1.,0.02);// 1% error on pressure
cur*=rndm.Gaus(1.,0.01); // 1% error on current
// write to ntuple
cond_data.Fill(pot,cur,temp,pres);
}
// Save the ntuple and close the file
cond_data.Write();
ofile.Close();
}This data written to this example n-tuple represents, in the statistical sense, three independent variables (Potential or Voltage, Pressure and Temperature), and one variable (Current) which depends on the others according to very simple laws, and an additional Gaussian smearing. This set of variables mimics a measurement of an electrical resistance while varying pressure and temperature.
Imagine your task now consists in finding the relations among the variables – of course without knowing the code used to generate them. You will see that the possibilities of the NTuple class enable you to perform this analysis task. Open the ROOT file (cond_data.root) written by the macro above in an interactive session and use a TBrowser to interactively inspect it:
You find the columns of your n-tuple written as leafs. Simply clicking on them you can obtain histograms of the variables!
Next, try the following commands at the shell prompt and in the interactive ROOT shell, respectively:
> root conductivity_experiment.root
Attaching file conductivity_experiment.root as _file0...
root [0] cond_data->Draw("Current:Potential")You just produced a correlation plot with one single line of code!
Try to extend the syntax typing for example
What do you obtain ?
Now try
It should have become clear from these examples how to navigate in such a multi-dimensional space of variables and unveil relations between variables using n-tuples.
For completeness, you find here a small macro to read the data back from a ROOT n-tuple
// Read the previously produced N-Tuple and print on screen
// its content
void read_ntuple_from_file(){
// Open a file, save the ntuple and close the file
TFile in_file("conductivity_experiment.root");
TNtuple* my_tuple;in_file.GetObject("cond_data",my_tuple);
float pot,cur,temp,pres; float* row_content;
cout << "Potential\tCurrent\tTemperature\tPressure\n";
for (int irow=0;irow<my_tuple->GetEntries();++irow){
my_tuple->GetEntry(irow);
row_content = my_tuple->GetArgs();
pot = row_content[0];
cur = row_content[1];
temp = row_content[2];
pres = row_content[3];
cout << pot << "\t" << cur << "\t" << temp
<< "\t" << pres << endl;
}
}The macro shows the easiest way of accessing the content of a n-tuple: after loading the n-tuple, its branches are assigned to variables and GetEntry(long) automatically fills them with the content for a specific row. By doing so, the logic for reading the n-tuple and the code to process it can be split and the source code remains clear.
It is also possible to write n-tuples of arbitrary type by using ROOT’s TBranch class. This is especially important as TNtuple::Fill() accepts only floats. The following macro creates the same n-tuple as before but the branches are booked directly. The Fill() function then fills the current values of the connected variables to the tree.
// Fill an n-tuple and write it to a file simulating measurement of
// conductivity of a material in different conditions of pressure
// and temperature using branches.
void write_ntuple_to_file_advanced(
const std::string& outputFileName="conductivity_experiment.root"
,unsigned int numDataPoints=1000000){
TFile ofile(outputFileName.c_str(),"RECREATE");
// Initialise the TNtuple
TTree cond_data("cond_data", "Example N-Tuple");
// define the variables and book them for the ntuple
float pot,cur,temp,pres;
cond_data.Branch("Potential", &pot, "Potential/F");
cond_data.Branch("Current", &cur, "Current/F");
cond_data.Branch("Temperature", &temp, "Temperature/F");
cond_data.Branch("Pressure", &pres, "Pressure/F");
for (int i=0;i<numDataPoints;++i){
// Fill it randomly to fake the acquired data
pot=gRandom->Uniform(0.,10.)*gRandom->Gaus(1.,0.01);
temp=gRandom->Uniform(250.,350.)+gRandom->Gaus(0.,0.3);
pres=gRandom->Uniform(0.5,1.5)*gRandom->Gaus(1.,0.02);
cur=pot/(10.+0.05*(temp-300.)-0.2*(pres-1.))*
gRandom->Gaus(1.,0.01);
// write to ntuple
cond_data.Fill();}
// Save the ntuple and close the file
cond_data.Write();
ofile.Close();
}The Branch() function requires a pointer to a variable and a definition of the variable type. The following table lists some of the possible values. Please note that ROOT is not checking the input and mistakes are likely to result in serious problems. This holds especially if values are read as another type than they have been written, e.g. when storing a variable as float and reading it as double.
List of variable types that can be used to define the type of a branch in ROOT:
| type | size | C++ | identifier |
|---|---|---|---|
| signed integer | 32 bit | int | I |
| 64 bit | long | L | |
| unsigned integer | 32 bit | unsigned int | i |
| 64 bit | unsigned long | l | |
| floating point | 32 bit | float | F |
| 64 bit | double | D | |
| boolean | - | bool | O |
Usually n-tuples or trees span over many files and it would be difficult to add them manually. ROOT thus kindly provides a helper class in the form of TChain. Its usage is shown in the following macro which is very similar to the previous example. The constructor of a TChain takes the name of the TTree (or TNuple) as an argument. The files are added with the function Add(fileName), where one can also use wild-cards as shown in the example.
// Read several previously produced N-Tuples and print on screen its
// content.
//
// you can easily create some files with the following statement:
//
// for i in 0 1 2 3 4 5; \\
// do root -l -x -b -q \\
// "write_ntuple_to_file.cxx \\
// (\"conductivity_experiment_${i}.root\", 100)"; \\
// done
void read_ntuple_with_chain(){
// initiate a TChain with the name of the TTree to be processed
TChain in_chain("cond_data");
in_chain.Add("conductivity_experiment*.root"); // add files,
// wildcards work
// define variables and assign them to the corresponding branches
float pot, cur, temp, pres;
in_chain.SetBranchAddress("Potential", &pot);
in_chain.SetBranchAddress("Current", &cur);
in_chain.SetBranchAddress("Temperature", &temp);
in_chain.SetBranchAddress("Pressure", &pres);
cout << "Potential\tCurrent\tTemperature\tPressure\n";
for (size_t irow=0; irow<in_chain.GetEntries(); ++irow){
in_chain.GetEntry(irow); // loads all variables that have
// been connected to branches
cout << pot << "\t" << cur << "\t" << temp <<
"\t" << pres << endl;
}
}Another very general and powerful way of processing a TChain is provided via the method TChain::Process(). This method takes as arguments an instance of a – user-implemented– class of type TSelector, and – optionally – the number of entries and the first entry to be processed. A template for the class TSelector is provided by the method TTree::MakeSelector, as is shown in the little macro makeSelector.C below.
It opens the n-tuple conductivity_experiment.root from the example above and creates from it the header file MySelector.h and a template to insert your own analysis code, MySelector.C.
{
// create template class for Selector to run on a tree
//////////////////////////////////////////////////////
//
// open root file containing the Tree
TFile f("conductivity_experiment.root");
// create TTree object from it
TTree *t; f.GetObject("cond_data",t);
// this generates the files MySelector.h and MySelector.C
t->MakeSelector("MySelector");
}The template contains the entry points Begin() and SlaveBegin() called before processing of the TChain starts, Process() called for every entry of the chain, and SlaveTerminate() and Terminate() called after the last entry has been processed. Typically, initialization like booking of histograms is performed in SlaveBegin(), the analysis, i.e. the selection of entries, calculations and filling of histograms, is done in Process(), and final operations like plotting and storing of results happen in SlaveTerminate() or Terminate().
The entry points SlaveBegin() and SlaveTerminate() are called on so-called slave nodes only if parallel processing via PROOF or PROOF lite is enabled, as will be explained below.
A simple example of a selector class is shown in the macro MySelector.C. The example is executed with the following sequence of commands:
> TChain *ch=new TChain("cond_data", "Chain for Example N-Tuple");
> ch->Add("conductivity_experiment*.root");
> ch->Process("MySelector.C+");As usual, the “+” appended to the name of the macro to be executed initiates the compilation of the MySelector.C with the system compiler in order to improve performance.
The code in MySelector.C, shown in the listing below, books some histograms in SlaveBegin() and adds them to the instance fOutput, which is of the class TList.4 The final processing in Terminate() allows to access histograms and store, display or save them as pictures. This is shown in the example via the TList fOutput. See the commented listing below for more details; most of the text is actually comments generated automatically by TTree::MakeSelector.
#define MySelector_cxx
// The class definition in MySelector.h has been generated automatically
// by the ROOT utility TTree::MakeSelector(). This class is derived
// from the ROOT class TSelector. For more information on the TSelector
// framework see $ROOTSYS/README/README.SELECTOR or the ROOT User Manual.
// The following methods are defined in this file:
// Begin(): called every time a loop on the tree starts,
// a convenient place to create your histograms.
// SlaveBegin(): called after Begin(), when on PROOF called only on the
// slave servers.
// Process(): called for each event, in this function you decide what
// to read and fill your histograms.
// SlaveTerminate: called at the end of the loop on the tree, when on PROOF
// called only on the slave servers.
// Terminate(): called at the end of the loop on the tree,
// a convenient place to draw/fit your histograms.
//
// To use this file, try the following session on your Tree T:
//
// root> T->Process("MySelector.C")
// root> T->Process("MySelector.C","some options")
// root> T->Process("MySelector.C+")
//
#include "MySelector.h"
#include <TH2.h>
#include <TStyle.h>
void MySelector::Begin(TTree * /*tree*/)
{
// The Begin() function is called at the start of the query.
// When running with PROOF Begin() is only called on the client.
// The tree argument is deprecated (on PROOF 0 is passed).
TString option = GetOption();
}
void MySelector::SlaveBegin(TTree * /*tree*/)
{
// The SlaveBegin() function is called after the Begin() function.
// When running with PROOF SlaveBegin() is called on each slave server.
// The tree argument is deprecated (on PROOF 0 is passed).
TString option = GetOption();
}
Bool_t MySelector::Process(Long64_t entry)
{
// The Process() function is called for each entry in the tree (or possibly
// keyed object in the case of PROOF) to be processed. The entry argument
// specifies which entry in the currently loaded tree is to be processed.
// It can be passed to either MySelector::GetEntry() or TBranch::GetEntry()
// to read either all or the required parts of the data. When processing
// keyed objects with PROOF, the object is already loaded and is available
// via the fObject pointer.
//
// This function should contain the "body" of the analysis. It can contain
// simple or elaborate selection criteria, run algorithms on the data
// of the event and typically fill histograms.
//
// The processing can be stopped by calling Abort().
//
// Use fStatus to set the return value of TTree::Process().
//
// The return value is currently not used.
return kTRUE;
}
void MySelector::SlaveTerminate()
{
// The SlaveTerminate() function is called after all entries or objects
// have been processed. When running with PROOF SlaveTerminate() is called
// on each slave server.
}
void MySelector::Terminate()
{
// The Terminate() function is the last function to be called during
// a query. It always runs on the client, it can be used to present
// the results graphically or save the results to file.
}PROOF liteThe processing of n-tuples via a selector function of type TSelector through TChain::Process(), as described at the end of the previous section, offers an additional advantage in particular for very large data sets: on distributed systems or multi-core architectures, portions of data can be processed in parallel, thus significantly reducing the execution time. On modern computers with multi-core CPUs or hardware-threading enabled, this allows a much faster turnaround of analyses, since all the available CPU power is used.
On distributed systems, a PROOF server and worker nodes have to be set up, as described in detail in the ROOT documentation. On a single computer with multiple cores, PROOF lite can be used instead. Try the following little macro, RunMySelector.C, which contains two extra lines compared to the example above (adjust the number of workers according to the number of CPU cores):
{// set up a TChain
TChain *ch=new TChain("cond_data", "My Chain for Example N-Tuple");
ch->Add("conductivity_experiment*.root");
// eventually, start Proof Lite on cores
TProof::Open("workers=4");
ch->SetProof();
ch->Process("MySelector.C+");}The first command, TProof::Open(const char*) starts a local PROOF server (if no arguments are specified, all cores will be used), and the command ch->SetProof(); enables processing of the chain using PROOF. Now, when issuing the command ch->Process("MySelector.C+);, the code in MySelector.C is compiled and executed on each slave node. The methods Begin() and Terminate() are executed on the master only. The list of n-tuple files is analysed, and portions of the data are assigned to the available slave processes. Histograms booked in SlaveBegin() exist in the processes on the slave nodes, and are filled accordingly. Upon termination, the PROOF master collects the histograms from the slaves and merges them. In Terminate() all merged histograms are available and can be inspected, analysed or stored. The histograms are handled via the instances fOutput of class TList in each slave process, and can be retrieved from this list after merging in Terminate.
To explore the power of this mechanism, generate some very large n-tuples using the script from the section Storing Arbitrary N-tuples - you could try 10 000 000 events (this results in a large n-tuple of about 160 MByte in size). You could also generate a large number of files and use wildcards to add the to the TChain. Now execute: > root -l RunMySelector.C and watch what happens:
Processing RunMySelector.C...
+++ Starting PROOF-Lite with 4 workers +++
Opening connections to workers: OK (4 workers)
Setting up worker servers: OK (4 workers)
PROOF set to parallel mode (4 workers)
Info in <TProofLite::SetQueryRunning>: starting query: 1
Info in <TProofQueryResult::SetRunning>: nwrks: 4
Info in <TUnixSystem::ACLiC>: creating shared library
~/DivingROOT/macros/MySelector_C.so
*==* ----- Begin of Job ----- Date/Time = Wed Feb 15 23:00:04 2012
Looking up for exact location of files: OK (4 files)
Looking up for exact location of files: OK (4 files)
Info in <TPacketizerAdaptive::TPacketizerAdaptive>:
Setting max number of workers per node to 4
Validating files: OK (4 files)
Info in <TPacketizerAdaptive::InitStats>:
fraction of remote files 1.000000
Info in <TCanvas::Print>:
file ResistanceDistribution.png has been created
*==* ----- End of Job ----- Date/Time = Wed Feb 15 23:00:08 2012
Lite-0: all output objects have been mergedLog files of the whole processing chain are kept in the directory ~.proof for each worker node. This is very helpful for debugging or if something goes wrong. As the method described here also works without using PROOF, the development work on an analysis script can be done in the standard way on a small subset of the data, and only for the full processing one would use parallelism via PROOF.
It is worth to remind the reader that the speed of typical data analysis programs limited by the I/O speed (for example the latencies implied by reading data from a hard drive). It is therefore expected that this limitation cannot be eliminated with the usage of any parallel analysis toolkit.
ROOT automatically applies compression algorithms on n-tuples to reduce the memory consumption. A value that is in most cases the same will consume only small space on your disk (but it has to be decompressed on reading). Nevertheless, you should think about the design of your n-tuples and your analyses as soon as the processing time exceeds some minutes.
Try to keep your n-tuples simple and use appropriate variable types. If your measurement has only a limited precision, it is needless to store it with double precision.
Experimental conditions that do not change with every single measurement should be stored in a separate tree. Although the compression can handle redundant values, the processing time increase with every variable that has to be filled.
The function SetCacheSize(long) specifies the size of the cache for reading a TTree object from a file. The default value is 30MB. A manual increase may help in certain situations. Please note that the caching mechanism can cover only one TTree object per TFile object.
You can select the branches to be covered by the caching algorithm with AddBranchToCache and deactivate unneeded branches with SetBranchStatus. This mechanism can result in a significant speed-up for simple operations on trees with many branches.
You can measure the performance easily with TTreePerfStats. The ROOT documentation on this class also includes an introductory example. For example, TTreePerfStats can show you that it is beneficial to store meta data and payload data separately, i.e. write the meta data tree in a bulk to a file at the end of your job instead of writing both trees interleaved.
ROOT offers the possibility to interface to Python via a set of bindings called PyROOT. Python is used in a wide variety of application areas and one of the most used scripting languages today. With the help of PyROOT it becomes possible to combine the power of a scripting language with ROOT tools. Introductory material to Python is available from many sources on the web, see e. g. http://docs.python.org.
The access to ROOT classes and their methods in PyROOT is almost identical to C++ macros, except for the special language features of Python, most importantly dynamic type declaration at the time of assignment. Coming back to our first example, simply plotting a function in ROOT, the following C++ code:
TF1 *f1 = new TF1("f2","[0]*sin([1]*x)/x",0.,10.);
f1->SetParameter(0,1);
f1->SetParameter(1,1);
f1->Draw();in Python becomes:
import ROOT
f1 = ROOT.TF1("f2","[0]*sin([1]*x)/x",0.,10.)
f1.SetParameter(0,1);
f1.SetParameter(1,1);
f1.Draw();A slightly more advanced example hands over data defined in the macro to the ROOT class TGraphErrors. Note that a Python array can be used to pass data between Python and ROOT. The first line in the Python script allows it to be executed directly from the operating system, without the need to start the script from python or the highly recommended powerful interactive shell ipython. The last line in the python script is there to allow you to have a look at the graphical output in the ROOT canvas before it disappears upon termination of the script.
Here is the C++ version:
void TGraphFit(){
//
// Draw a graph with error bars and fit a function to it
//
gStyle->SetOptFit(111) ; //superimpose fit results
// make nice Canvas
TCanvas *c1 = new TCanvas("c1" ,"Daten" ,200 ,10 ,700 ,500) ;
c1->SetGrid( ) ;
//define some data points ...
const Int_t n = 10;
Float_t x[n] = {-0.22, 0.1, 0.25, 0.35, 0.5, 0.61, 0.7, 0.85, 0.89, 1.1};
Float_t y[n] = {0.7, 2.9, 5.6, 7.4, 9., 9.6, 8.7, 6.3, 4.5, 1.1};
Float_t ey[n] = {.8 ,.7 ,.6 ,.5 ,.4 ,.4 ,.5 ,.6 ,.7 ,.8};
Float_t ex[n] = {.05 ,.1 ,.07 ,.07 ,.04 ,.05 ,.06 ,.07 ,.08 ,.05};
// and hand over to TGraphErros object
TGraphErrors *gr = new TGraphErrors(n,x,y,ex,ey);
gr->SetTitle("TGraphErrors with Fit") ;
gr->Draw("AP");
// now perform a fit (with errors in x and y!)
gr->Fit("gaus");
c1->Update();
}In Python it looks like this:
#
# Draw a graph with error bars and fit a function to it
#
from ROOT import gStyle, TCanvas, TGraphErrors
from array import array
gStyle.SetOptFit (111) # superimpose fit results
c1=TCanvas("c1" ,"Data" ,200 ,10 ,700 ,500) #make nice
c1.SetGrid ()
#define some data points . . .
x = array('f', (-0.22, 0.1, 0.25, 0.35, 0.5, 0.61, 0.7, 0.85, 0.89, 1.1) )
y = array('f', (0.7, 2.9, 5.6, 7.4, 9., 9.6, 8.7, 6.3, 4.5, 1.1) )
ey = array('f', (.8 ,.7 ,.6 ,.5 ,.4 ,.4 ,.5 ,.6 ,.7 ,.8) )
ex = array('f', (.05 ,.1 ,.07 ,.07 ,.04 ,.05 ,.06 ,.07 ,.08 ,.05) )
nPoints=len ( x )
# . . . and hand over to TGraphErros object
gr=TGraphErrors ( nPoints , x , y , ex , ey )
gr.SetTitle("TGraphErrors with Fit")
gr.Draw ( "AP" ) ;
gr.Fit("gaus")
c1.Update ()
# request user action before ending (and deleting graphics window)
raw_input('Press <ret> to end -> ')Comparing the C++ and Python versions in these two examples, it now should be clear how easy it is to convert any ROOT Macro in C++ to a Python version.
As another example, let us revisit macro3 from Chapter 4. A straight-forward Python version relying on the ROOT class TMath:
# Builds a polar graph in a square Canvas.
from ROOT import TGraphPolar, TCanvas, TMath
from array import array
c = TCanvas("myCanvas","myCanvas",600,600)
rmin = 0.
rmax = TMath.Pi()*6.
npoints = 300
r = array('d',[0]*npoints)
theta = array('d',[0]*npoints)
for ipt in xrange(0,npoints):
r[ipt] = ipt*(rmax-rmin)/npoints+rmin
theta[ipt] = TMath.Sin(r[ipt])
grP1 = TGraphPolar(npoints,r,theta)
grP1.SetTitle("A Fan")
grP1.SetLineWidth(3)
grP1.SetLineColor(2)
grP1.DrawClone("L")
raw_input("Press enter to exit.")You may have noticed already that there are some Python modules providing functionality similar to ROOT classes, which fit more seamlessly into your Python code.
A more “pythonic” version of the above macro3 would use a replacement of the ROOT class TMath for the provisioning of data to TGraphPolar. With the math package, the part of the code becomes
import math
from array import array
from ROOT import TCanvas , TGraphPolar
...
ipt=range(0,npoints)
r=array('d',map(lambda x: x*(rmax-rmin)/(npoints-1.)+rmin,ipt))
theta=array('d',map(math.sin,r))
e=array('d',npoints*[0.])
...This example combines comfortable handling of arrays in Python to define variable bin sizes of a ROOT histogram. All we need to know is the interface of the relevant ROOT class and its methods (from the ROOT documentation):
Here is the Python code:
import ROOT
from array import array
arrBins = array('d' ,(1 ,4 ,9 ,16) ) # array of bin edges
histo = ROOT.TH1F("hist", "hist", len(arrBins)-1, arrBins)
# fill it with equally spaced numbers
for i in range (1 ,16) :
histo.Fill(i)
histo.Draw ()The ROOT interpreter and type sytem offer interesting possibilities when it comes to JITting of C++ code. Take for example this header file, containing a class and a function.
// file cpp2pythonExample.h
#include "stdio.h"
class A{
public:
A(int i):m_i(i){}
int getI() const {return m_i;}
private:
int m_i=0;
};
void printA(const A& a ){
printf ("The value of A instance is %i.\n",a.getI());
}>>> import ROOT
>>> ROOT.gInterpreter.ProcessLine('#include "cpp2pythonExample.h"')
>>> a = ROOT.A(123)
>>> ROOT.printA(a)
The value of A instance is 123.This example might seem trivial, but it shows a powerful ROOT feature. C++ code can be JITted within PyROOT and the entities defined in C++ can be transparently used in Python!
This is the end of our guided tour for beginners through ROOT. There is still a lot coming to mind to be said, but by now you are experienced enough to use the ROOT documentation, most importantly the ROOT home page and the ROOT reference guide with the documentation of all ROOT classes, or the ROOT users manual.
A very useful way for you to continue exploring ROOT is to study the examples in the sub-directory tutorials/ of any ROOT installation.
There are some powerful features of ROOT which were not treated in this document, e.g. packages named RooFit and RooStats providing an advanced framework for model building, fitting and statistical analysis. The ROOT namespace TMVA offers multi-variate analysis tools including an artificial neural network and many other advanced tools for classification problems. The remarkable ability of ROOT to handle large data volumes was already mentioned in this guide, implemented through the class TTree. But there is still much more for you to explore!
End of this guide … but hopefully not of your interaction with ROOT !
Matsumoto, Makoto. 1997. “Mersenne Twister Home Page.” http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html.
Silin, I.N. 1983. “FUMILI.” CERN Program Library d510.
The Root Reference Guide. 2023. https://root.cern/doc/master/.
The Root Users Guide. 2020. https://root.cern/manual/.
“What is Cling.” 2015. https://root.cern/cling/.
All ROOT classes’ names start with the letter T. A notable exception is RooFit. In this context all classes’ names are of the form Roo*. Starting with ROOT7, all names start with and R.↩
To optimise the memory usage you might go for one byte (TH1C), short (TH1S), integer (TH1I), long64 (TH1L) or double-precision (TH1D) bin-content.↩
“Monte Carlo” simulation means that random numbers play a role here which is as crucial as in games of pure chance in the Casino of Monte Carlo.↩
The usage of fOutput is not really needed for this simple example, but it allows re-usage of the exact code in parallel processing with PROOF (see next section).↩