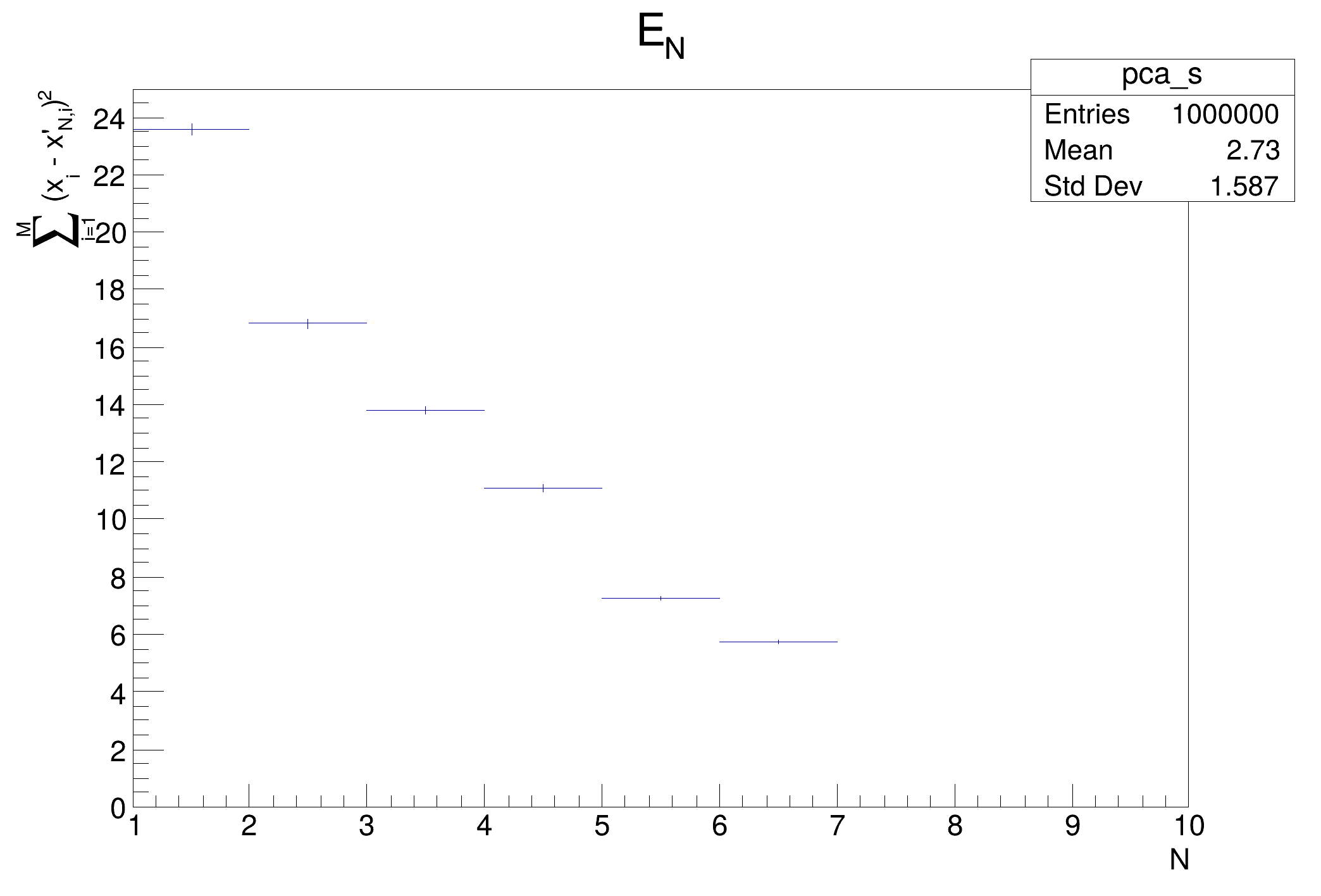
Principal Components Analysis (PCA) example.
Example of using TPrincipal as a stand alone class.
I create n-dimensional data points, where c = trunc(n / 5) + 1 are correlated with the rest n - c randomly distributed variables.
Based on principal.C by Rene Brun and Christian Holm Christensen
*************************************************
* Principal Component Analysis *
* *
* Number of variables: 10 *
* Number of data points: 10000 *
* Number of dependent variables: 3 *
* *
*************************************************
Variable # | Mean Value | Sigma | Eigenvalue
-------------+------------+------------+------------
0 | 4.994 | 0.9926 | 0.3856
1 | 8.011 | 2.824 | 0.112
2 | 2.017 | 1.992 | 0.1031
3 | 4.998 | 0.9952 | 0.1022
4 | 8.019 | 2.794 | 0.09998
5 | 1.976 | 2.009 | 0.0992
6 | 4.996 | 0.9996 | 0.09794
7 | 35.01 | 5.147 | 1.409e-16
8 | 30.01 | 5.041 | 2.723e-16
9 | 28.04 | 4.644 | 4.578e-16
Writing on file "pca.C" ... done
from ROOT import TPrincipal, gRandom, TBrowser, vector
n = 10
m = 10000
print ("""*************************************************
* Principal Component Analysis *
* *
* Number of variables: {0:4d} *
* Number of data points: {1:8d} *
* Number of dependent variables: {2:4d} *
* *
*************************************************""".
format(n, m, c))
randomNum = gRandom
data = vector('double')()
if j % 3 == 0:
elif j % 3 == 1:
else:
for k
in range(n - c - j):
data[n - c + j] += data[k]
b =
TBrowser(
"principalBrowser", principal)
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
Option_t Option_t TPoint TPoint const char GetTextMagnitude GetFillStyle GetLineColor GetLineWidth GetMarkerStyle GetTextAlign GetTextColor GetTextSize void char Point_t Rectangle_t WindowAttributes_t Float_t Float_t Float_t Int_t Int_t UInt_t UInt_t Rectangle_t Int_t Int_t Window_t TString Int_t GCValues_t GetPrimarySelectionOwner GetDisplay GetScreen GetColormap GetNativeEvent const char const char dpyName wid window const char font_name cursor keysym reg const char only_if_exist regb h Point_t winding char text const char depth char const char Int_t count const char ColorStruct_t color const char Pixmap_t Pixmap_t PictureAttributes_t attr const char char ret_data h unsigned char height h Atom_t Int_t ULong_t ULong_t unsigned char prop_list Atom_t Atom_t Atom_t Time_t format
Using a TBrowser one can browse all ROOT objects.
Principal Components Analysis (PCA)
- Authors
- Juan Fernando, Jaramillo Botero
Definition in file principal.py.