import ROOT
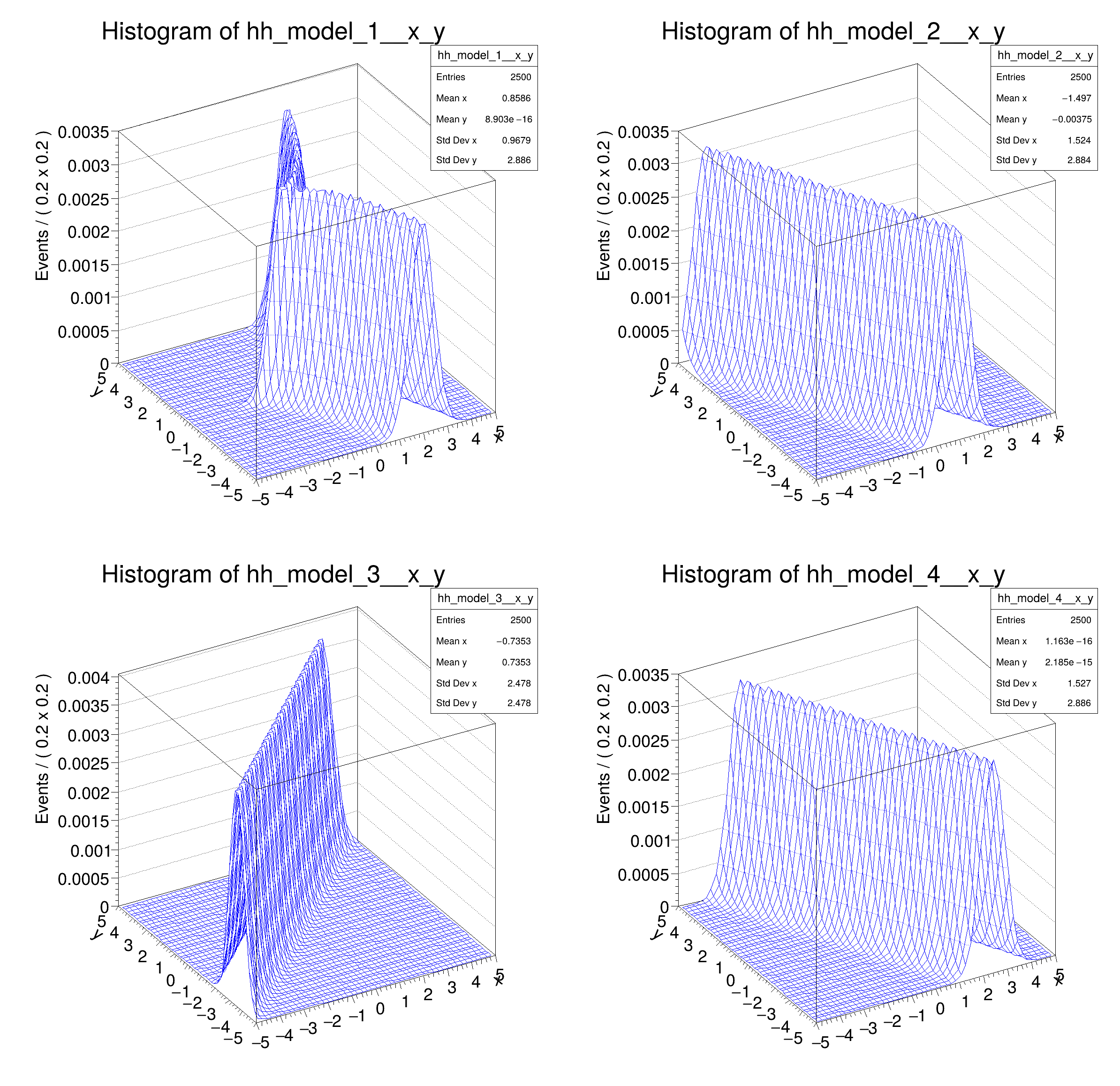
model_1 =
ROOT.RooGaussian(
"model_1",
"Gaussian with shifting mean", x, fy_1, sigma)
model_2 =
ROOT.RooGaussian(
"model_2",
"Gaussian with shifting mean", x, fy_2, sigma)
model_3 =
ROOT.RooGaussian(
"model_3",
"Gaussian with shifting mean", x, fy_3, sigma)
model_4 =
ROOT.RooGaussian(
"model_4",
"Gaussian with shifting mean", x, fy_4, sigma)
c =
ROOT.TCanvas(
"rf302_utilfuncs",
"rf302_utilfuncs", 800, 800)
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
[#0] WARNING:InputArguments -- The parameter 'sigma' with range [-inf, inf] of the RooGaussian 'model_1' exceeds the safe range of (0, inf). Advise to limit its range.
[#0] WARNING:InputArguments -- The parameter 'sigma' with range [-inf, inf] of the RooGaussian 'model_2' exceeds the safe range of (0, inf). Advise to limit its range.
[#0] WARNING:InputArguments -- The parameter 'sigma' with range [-inf, inf] of the RooGaussian 'model_3' exceeds the safe range of (0, inf). Advise to limit its range.
[#0] WARNING:InputArguments -- The parameter 'sigma' with range [-inf, inf] of the RooGaussian 'model_4' exceeds the safe range of (0, inf). Advise to limit its range.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_1_Int[x,y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_2_Int[x,y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_3_Int[x,y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_4_Int[x,y]) using numeric integrator RooIntegrator1D to calculate Int(y)