 |
ROOT 6.12/07 Reference Guide |
 |
ROOT 6.12/07 Reference Guide |

 Tutorial illustrating use and precision of the Double32_t data type You must run this tutorial with ACLIC: a dictionary will be automatically created.
Tutorial illustrating use and precision of the Double32_t data type You must run this tutorial with ACLIC: a dictionary will be automatically created.
The following cases are supported for streaming a Double32_t type depending on the range declaration in the comment field of the data member:
| Case | Declaration |
|---|---|
| A | Double32_t fNormal; |
| B | Double32_t fTemperature; //[0,100] |
| C | Double32_t fCharge; //[-1,1,2] |
| D | Double32_t fVertex[3]; //[-30,30,10] |
| E | Double32_t fChi2; //[0,0,6] |
| F | Int_t fNsp; Double32_t* fPointValue; //[fNsp][0,3] |
Case B has more precision than case A: 9 to 10 significative digits and 6 to 7 digits respectively. The range specifier has the general format: [xmin,xmax] or [xmin,xmax,nbits]. Examples
Lets assume an original variable double x. When using the format 0,0,8 you get the best relative precision when storing and reading back the truncated x, say xt. The variance of (x-xt)/x will be better than when specifying a range for the same number of bits. However the precision relative to the range (x-xt)/(xmax-xmin) will be worst, and vice-versa. The format [0,0,8] is also interesting when the range of x is infinite or unknown.
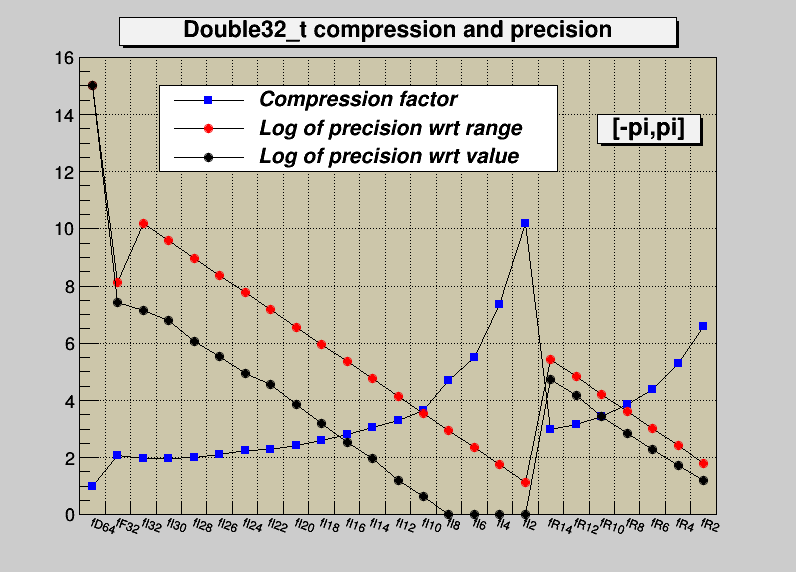
Definition in file double32.C.