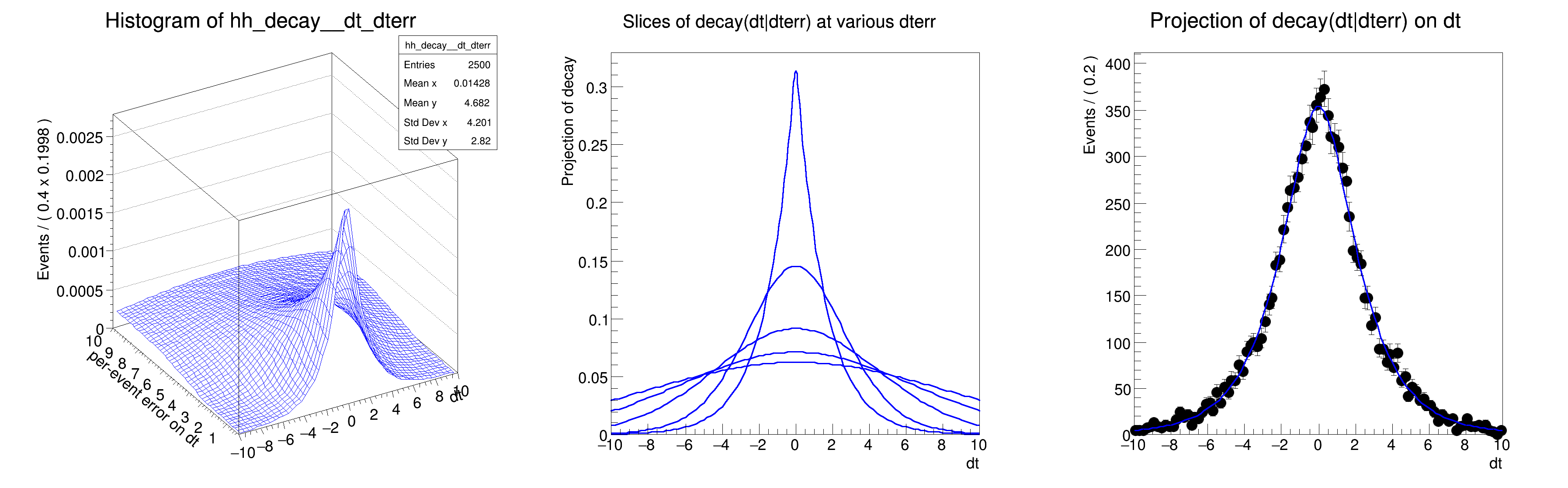
Multidimensional models: conditional p.d.f. with per-event errors
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 bias 0.00000e+00 2.00000e+00 -1.00000e+01 1.00000e+01
2 sigma 1.00000e+00 4.50000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=23876.4 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 bias 0.00000e+00 2.00000e+00 2.01358e-01 -1.70342e+02
2 sigma 1.00000e+00 4.50000e-01 1.63378e-01 8.62474e+01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=23876.2 FROM MIGRAD STATUS=CONVERGED 30 CALLS 31 TOTAL
EDM=3.03467e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 bias 5.26463e-03 1.72103e-02 1.83632e-04 1.00797e-01
2 sigma 9.87130e-01 2.04183e-02 7.70435e-04 2.52620e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
2.962e-04 -4.402e-06
-4.402e-06 4.169e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.01253 1.000 -0.013
2 0.01253 -0.013 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=23876.2 FROM HESSE STATUS=OK 12 CALLS 43 TOTAL
EDM=3.12688e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 bias 5.26463e-03 1.72105e-02 3.67263e-05 5.26463e-04
2 sigma 9.87130e-01 2.04260e-02 3.08174e-05 -9.62778e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
2.962e-04 -4.786e-06
-4.786e-06 4.172e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.01361 1.000 -0.014
2 0.01361 -0.014 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(gm1_conv_exp(-abs(@0)/@1)_dt_tau_[decay_gm]_Int[dt,dterr]) using numeric integrator RooIntegrator1D to calculate Int(dterr)
[#1] INFO:Plotting -- RooAbsReal::plotOn(decay_gm) plot on dt averages using data variables (dterr)
[#1] INFO:Plotting -- RooDataWeightedAverage::ctor(decay_gmDataWgtAvg) constructing data weighted average of function decay_gm_Norm[dt] over 100 data points of (dterr) with a total weight of 10000
.........................................................................................................................................................................................................................
{
RooRealVar dterr(
"dterr",
"per-event error on dt", 0.01, 10);
RooDataSet *expDataDterr = pdfDtErr.generate(dterr, 10000);
for (
Int_t ibin = 0; ibin < 100; ibin += 20) {
dterr.setBin(ibin);
}
TCanvas *
c =
new TCanvas(
"rf306_condpereventerrors",
"rf306_condperventerrors", 1200, 400);
gPad->SetLeftMargin(0.20);
gPad->SetLeftMargin(0.15);
gPad->SetLeftMargin(0.15);
}
virtual RooPlot * plotOn(RooPlot *frame, const RooCmdArg &arg1=RooCmdArg::none(), const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none(), const RooCmdArg &arg6=RooCmdArg::none(), const RooCmdArg &arg7=RooCmdArg::none(), const RooCmdArg &arg8=RooCmdArg::none()) const
Calls RooPlot* plotOn(RooPlot* frame, const RooLinkedList& cmdList) const ;.
RooDataSet is a container class to hold unbinned data.
Single or double sided decay function that can be analytically convolved with any RooResolutionModel ...
Class RooGaussModel implements a RooResolutionModel that models a Gaussian distribution.
Landau distribution p.d.f.
A RooPlot is a plot frame and a container for graphics objects within that frame.
static RooPlot * frame(const RooAbsRealLValue &var, Double_t xmin, Double_t xmax, Int_t nBins)
Create a new frame for a given variable in x.
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
RooRealVar represents a variable that can be changed from the outside.
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title.
virtual void SetLineColor(Color_t lcolor)
Set the line color.
virtual void Draw(Option_t *option="")
Draw this histogram with options.
RooCmdArg YVar(const RooAbsRealLValue &var, const RooCmdArg &arg=RooCmdArg::none())
RooConstVar & RooConst(Double_t val)
RooCmdArg ConditionalObservables(const RooArgSet &set)
RooCmdArg ProtoData(const RooDataSet &protoData, Bool_t randomizeOrder=kFALSE, Bool_t resample=kFALSE)
RooCmdArg ProjWData(const RooAbsData &projData, Bool_t binData=kFALSE)
RooCmdArg Binning(const RooAbsBinning &binning)
RooCmdArg Normalization(Double_t scaleFactor)
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...