Total Initial distance square = 8.65172e+07
Total final distance square 19988
****************************************
Minimizer is Minuit / Migrad
MinFCN = 19988
NDf = 0
Edm = 6.31385e-10
NCalls = 257
Par_0 = 10.3552 +/- 0.39454
Par_1 = 19.9602 +/- 0.0689483
Par_2 = 0.999198 +/- 0.0444211
Par_3 = 2.00379 +/- 0.00780946
(int) 0
#include <cassert>
void line(
double t,
const double *p,
double &
x,
double &
y,
double &z) {
z = t;
}
struct SumDistance2 {
double distance2(
double x,
double y,
double z,
const double *p) {
return d2;
}
assert(fGraph != 0);
double *
x = fGraph->
GetX();
double *
y = fGraph->
GetY();
double * z = fGraph->
GetZ();
int npoints = fGraph->
GetN();
for (int i = 0; i < npoints; ++i) {
double d = distance2(
x[i],
y[i],z[i],par);
}
std::cout <<
"Total Initial distance square = " <<
sum << std::endl;
}
}
};
{
double p0[4] = {10,20,1,2};
double err = 1;
}
double pStart[4] = {1,1,1,1};
if (!ok) {
Error(
"line3Dfit",
"Line3D Fit failed");
return 1;
}
std::cout <<
"Total final distance square " << result.
MinFcnValue() << std::endl;
double t0 = 0;
double dt = 10;
for (
int i = 0; i <
n;++i) {
}
for (
int i = 0; i <
n;++i) {
}
return 0;
}
return line3Dfit();
}
static const double x1[5]
void Error(const char *location, const char *msgfmt,...)
Use this function in case an error occurred.
TGLVector3 Cross(const TGLVector3 &v1, const TGLVector3 &v2)
TRObject operator()(const T1 &t1) const
R__EXTERN TRandom * gRandom
R__EXTERN TStyle * gStyle
const ParameterSettings & ParSettings(unsigned int i) const
get the parameter settings for the i-th parameter (const method)
class containg the result of the fit and all the related information (fitted parameter values,...
const double * GetParams() const
parameter values (return const pointer)
void Print(std::ostream &os, bool covmat=false) const
print the result and optionaly covariance matrix and correlations
double MinFcnValue() const
Return value of the objective function (chi2 or likelihood) used in the fit.
Fitter class, entry point for performing all type of fits.
bool FitFCN(unsigned int npar, Function &fcn, const double *params=0, unsigned int dataSize=0, bool chi2fit=false)
Fit using the a generic FCN function as a C++ callable object implementing double () (const double *)...
bool SetFCN(unsigned int npar, Function &fcn, const double *params=0, unsigned int dataSize=0, bool chi2fit=false)
Set a generic FCN function as a C++ callable object implementing double () (const double *) Note that...
const FitResult & Result() const
get fit result
const FitConfig & Config() const
access to the fit configuration (const method)
void SetStepSize(double err)
set the step size
Documentation for class Functor class.
virtual void SetLineColor(Color_t lcolor)
Set the line color.
Graphics object made of three arrays X, Y and Z with the same number of points each.
virtual void SetPoint(Int_t i, Double_t x, Double_t y)
Set x and y values for point number i.
virtual void Draw(Option_t *chopt="")
Draw this graph with its current attributes.
A 3-dimensional polyline.
virtual void SetPoint(Int_t point, Double_t x, Double_t y, Double_t z)
Set point n to x, y, z.
virtual void Draw(Option_t *option="")
Draw this 3-D polyline with its current attributes.
virtual Double_t Gaus(Double_t mean=0, Double_t sigma=1)
Samples a random number from the standard Normal (Gaussian) Distribution with the given mean and sigm...
virtual Double_t Uniform(Double_t x1=1)
Returns a uniform deviate on the interval (0, x1).
void SetOptStat(Int_t stat=1)
The type of information printed in the histogram statistics box can be selected via the parameter mod...
void SetOptFit(Int_t fit=1)
The type of information about fit parameters printed in the histogram statistics box can be selected ...
SVector< T, D > Unit(const SVector< T, D > &rhs)
Unit.
T Mag2(const SVector< T, D > &rhs)
Vector magnitude square Template to compute .
static uint64_t sum(uint64_t i)

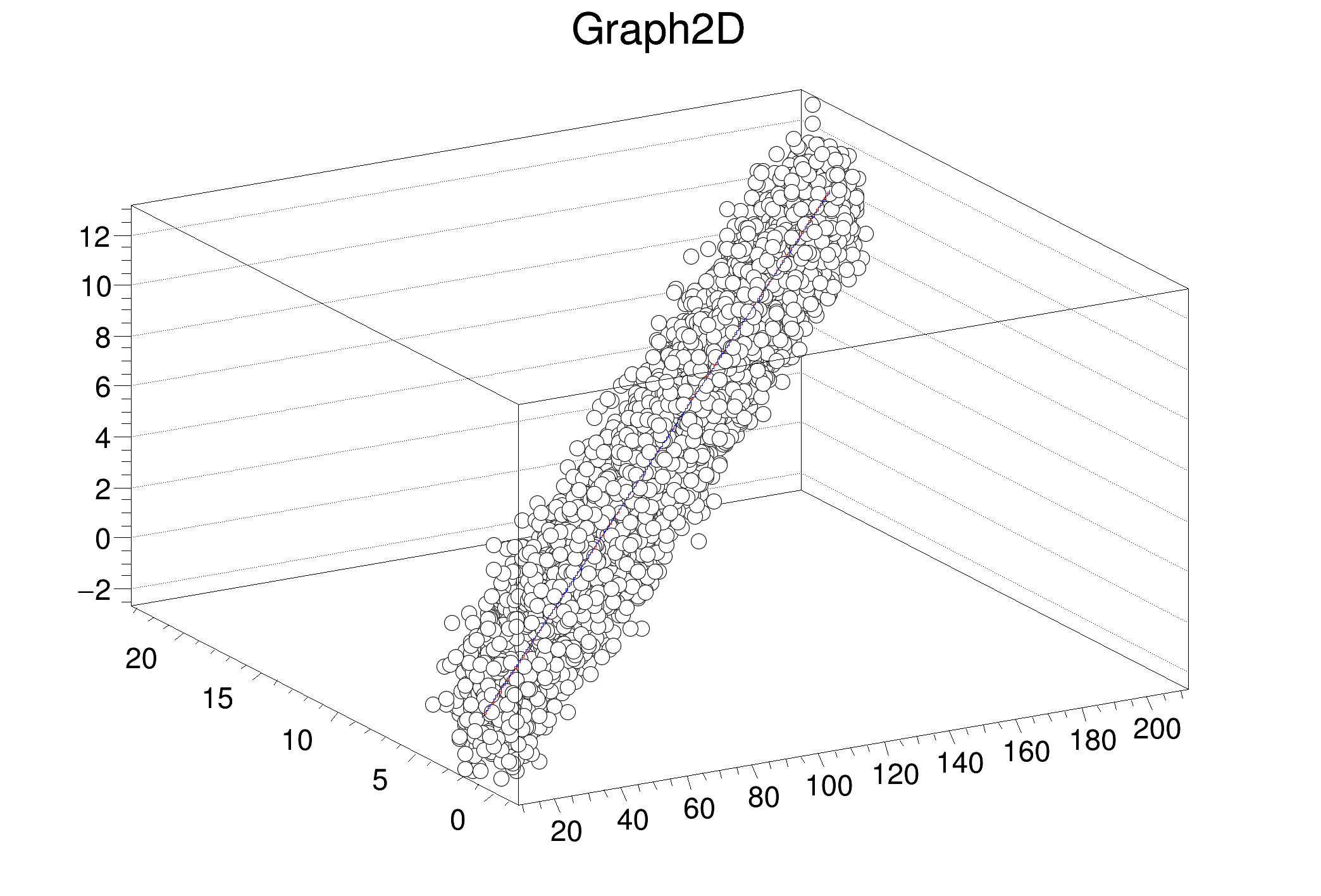
 Fitting of a TGraph2D with a 3D straight line
Fitting of a TGraph2D with a 3D straight line