+
class TMultiDimFit
-
library: libHist
#include "TMultiDimFit.h"
Display options:
Show inherited
Show non-public

class TMultiDimFit: public TNamed
/*

Multidimensional Fits in ROOT


Overview

A common problem encountered in different fields of applied science is to find an expression for one physical quantity in terms of several others, which are directly measurable.

An example in high energy physics is the evaluation of the momentum of a charged particle from the observation of its trajectory in a magnetic field. The problem is to relate the momentum of the particle to the observations, which may consists of of positional measurements at intervals along the particle trajectory.

The exact functional relationship between the measured quantities (e.g., the space-points) and the dependent quantity (e.g., the momentum) is in general not known, but one possible way of solving the problem, is to find an expression which reliably approximates the dependence of the momentum on the observations.

This explicit function of the observations can be obtained by a least squares fitting procedure applied to a representive sample of the data, for which the dependent quantity (e.g., momentum) and the independent observations are known. The function can then be used to compute the quantity of interest for new observations of the independent variables.

This class TMultiDimFit implements such a procedure in ROOT. It is largely based on the CERNLIB MUDIFI package [2]. Though the basic concepts are still sound, and therefore kept, a few implementation details have changed, and this class can take advantage of MINUIT [4] to improve the errors of the fitting, thanks to the class TMinuit.

In [5] and [6] H. Wind demonstrates the utility of this procedure in the context of tracking, magnetic field parameterisation, and so on. The outline of the method used in this class is based on Winds discussion, and I refer these two excellents text for more information.

And example of usage is given in $ROOTSYS/tutorials/fit/multidimfit.C.


The Method

Let $ D$ by the dependent quantity of interest, which depends smoothly on the observable quantities $ x_1, \ldots, x_N$, which we'll denote by $ \mathbf{x}$. Given a training sample of $ M$ tuples of the form, (TMultiDimFit::AddRow)

$\displaystyle \left(\mathbf{x}_j, D_j, E_j\right)\quad, $

where $ \mathbf{x}_j = (x_{1,j},\ldots,x_{N,j})$ are $ N$ independent variables, $ D_j$ is the known, quantity dependent at $ \mathbf{x}_j$, and $ E_j$ is the square error in $ D_j$, the class TMultiDimFit will try to find the parameterization

$\displaystyle D_p(\mathbf{x}) = \sum_{l=1}^{L} c_l \prod_{i=1}^{N} p_{li}\left(x_i\right) = \sum_{l=1}^{L} c_l F_l(\mathbf{x})$ (1)

such that

$\displaystyle S \equiv \sum_{j=1}^{M} \left(D_j - D_p\left(\mathbf{x}_j\right)\right)^2$ (2)

is minimal. Here $ p_{li}(x_i)$ are monomials, or Chebyshev or Legendre polynomials, labelled $ l = 1, \ldots, L$, in each variable $ x_i$, $ i=1, \ldots, N$.

So what TMultiDimFit does, is to determine the number of terms $ L$, and then $ L$ terms (or functions) $ F_l$, and the $ L$ coefficients $ c_l$, so that $ S$ is minimal (TMultiDimFit::FindParameterization).

Of course it's more than a little unlikely that $ S$ will ever become exact zero as a result of the procedure outlined below. Therefore, the user is asked to provide a minimum relative error $ \epsilon$ (TMultiDimFit::SetMinRelativeError), and $ S$ will be considered minimized when

$\displaystyle R = \frac{S}{\sum_{j=1}^M D_j^2} < \epsilon $

Optionally, the user may impose a functional expression by specifying the powers of each variable in $ L$ specified functions $ F_1, \ldots, F_L$ (TMultiDimFit::SetPowers). In that case, only the coefficients $ c_l$ is calculated by the class.


Limiting the Number of Terms

As always when dealing with fits, there's a real chance of over fitting. As is well-known, it's always possible to fit an $ N-1$ polynomial in $ x$ to $ N$ points $ (x,y)$ with $ \chi^2 = 0$, but the polynomial is not likely to fit new data at all [1]. Therefore, the user is asked to provide an upper limit, $ L_{max}$ to the number of terms in $ D_p$ (TMultiDimFit::SetMaxTerms).

However, since there's an infinite number of $ F_l$ to choose from, the user is asked to give the maximum power. $ P_{max,i}$, of each variable $ x_i$ to be considered in the minimization of $ S$ (TMultiDimFit::SetMaxPowers).

One way of obtaining values for the maximum power in variable $ i$, is to perform a regular fit to the dependent quantity $ D$, using a polynomial only in $ x_i$. The maximum power is $ P_{max,i}$ is then the power that does not significantly improve the one-dimensional least-square fit over $ x_i$ to $ D$ [5].

There are still a huge amount of possible choices for $ F_l$; in fact there are $ \prod_{i=1}^{N} (P_{max,i} + 1)$ possible choices. Obviously we need to limit this. To this end, the user is asked to set a power control limit, $ Q$ (TMultiDimFit::SetPowerLimit), and a function $ F_l$ is only accepted if

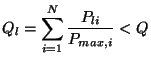
$\displaystyle Q_l = \sum_{i=1}^{N} \frac{P_{li}}{P_{max,i}} < Q $

where $ P_{li}$ is the leading power of variable $ x_i$ in function $ F_l$. (TMultiDimFit::MakeCandidates). So the number of functions increase with $ Q$ (1, 2 is fine, 5 is way out).

Gram-Schmidt Orthogonalisation

To further reduce the number of functions in the final expression, only those functions that significantly reduce $ S$ is chosen. What `significant' means, is chosen by the user, and will be discussed below (see 2.3).

The functions $ F_l$ are generally not orthogonal, which means one will have to evaluate all possible $ F_l$'s over all data-points before finding the most significant [1]. We can, however, do better then that. By applying the modified Gram-Schmidt orthogonalisation algorithm [5] [3] to the functions $ F_l$, we can evaluate the contribution to the reduction of $ S$ from each function in turn, and we may delay the actual inversion of the curvature-matrix (TMultiDimFit::MakeGramSchmidt).

So we are let to consider an $ M\times L$ matrix $ \mathsf{F}$, an element of which is given by

$\displaystyle f_{jl} = F_j\left(x_{1j} , x_{2j}, \ldots, x_{Nj}\right) = F_l(\mathbf{x}_j) $   with$\displaystyle  j=1,2,\ldots,M,$ (3)

where $ j$ labels the $ M$ rows in the training sample and $ l$ labels $ L$ functions of $ N$ variables, and $ L \leq M$. That is, $ f_{jl}$ is the term (or function) numbered $ l$ evaluated at the data point $ j$. We have to normalise $ \mathbf{x}_j$ to $ [-1,1]$ for this to succeed [5] (TMultiDimFit::MakeNormalized). We then define a matrix $ \mathsf{W}$ of which the columns $ \mathbf{w}_j$ are given by
$\displaystyle \mathbf{w}_1$ $\displaystyle =$ $\displaystyle \mathbf{f}_1 = F_1\left(\mathbf x_1\right)$ (4)
$\displaystyle \mathbf{w}_l$ $\displaystyle =$ $\displaystyle \mathbf{f}_l - \sum^{l-1}_{k=1} \frac{\mathbf{f}_l \bullet \mathbf{w}_k}{\mathbf{w}_k^2}\mathbf{w}_k .$ (5)

and $ \mathbf{w}_{l}$ is the component of $ \mathbf{f}_{l}$ orthogonal to $ \mathbf{w}_{1}, \ldots, \mathbf{w}_{l-1}$. Hence we obtain [3],

$\displaystyle \mathbf{w}_k\bullet\mathbf{w}_l = 0$   if$\displaystyle  k \neq l\quad.$ (6)

We now take as a new model $ \mathsf{W}\mathbf{a}$. We thus want to minimize

$\displaystyle S\equiv \left(\mathbf{D} - \mathsf{W}\mathbf{a}\right)^2\quad,$ (7)

where $ \mathbf{D} = \left(D_1,\ldots,D_M\right)$ is a vector of the dependent quantity in the sample. Differentiation with respect to $ a_j$ gives, using (6),

$\displaystyle \mathbf{D}\bullet\mathbf{w}_l - a_l\mathbf{w}_l^2 = 0$ (8)

or

$\displaystyle a_l = \frac{\mathbf{D}_l\bullet\mathbf{w}_l}{\mathbf{w}_l^2}$ (9)

Let $ S_j$ be the sum of squares of residuals when taking $ j$ functions into account. Then

$\displaystyle S_l = \left[\mathbf{D} - \sum^l_{k=1} a_k\mathbf{w}_k\right]^2 = ... ...2 - 2\mathbf{D} \sum^l_{k=1} a_k\mathbf{w}_k + \sum^l_{k=1} a_k^2\mathbf{w}_k^2$ (10)

Using (9), we see that
$\displaystyle S_l$ $\displaystyle =$ $\displaystyle \mathbf{D}^2 - 2 \sum^l_{k=1} a_k^2\mathbf{w}_k^2 + \sum^j_{k=1} a_k^2\mathbf{w}_k^2$  
  $\displaystyle =$ $\displaystyle \mathbf{D}^2 - \sum^l_{k=1} a_k^2\mathbf{w}_k^2$  
  $\displaystyle =$ $\displaystyle \mathbf{D}^2 - \sum^l_{k=1} \frac{\left(\mathbf D\bullet \mathbf w_k\right)}{\mathbf w_k^2}$ (11)

So for each new function $ F_l$ included in the model, we get a reduction of the sum of squares of residuals of $ a_l^2\mathbf{w}_l^2$, where $ \mathbf{w}_l$ is given by (4) and $ a_l$ by (9). Thus, using the Gram-Schmidt orthogonalisation, we can decide if we want to include this function in the final model, before the matrix inversion.


Function Selection Based on Residual

Supposing that $ L-1$ steps of the procedure have been performed, the problem now is to consider the $ L^{\mbox{th}}$ function.

The sum of squares of residuals can be written as

$\displaystyle S_L = \textbf{D}^T\bullet\textbf{D} - \sum^L_{l=1}a^2_l\left(\textbf{w}_l^T\bullet\textbf{w}_l\right)$ (12)

where the relation (9) have been taken into account. The contribution of the $ L^{\mbox{th}}$ function to the reduction of S, is given by

$\displaystyle \Delta S_L = a^2_L\left(\textbf{w}_L^T\bullet\textbf{w}_L\right)$ (13)

Two test are now applied to decide whether this $ L^{\mbox{th}}$ function is to be included in the final expression, or not.


Test 1

Denoting by $ H_{L-1}$ the subspace spanned by $ \textbf{w}_1,\ldots,\textbf{w}_{L-1}$ the function $ \textbf {w}_L$ is by construction (see (4)) the projection of the function $ F_L$ onto the direction perpendicular to $ H_{L-1}$. Now, if the length of $ \textbf {w}_L$ (given by $ \textbf{w}_L\bullet\textbf{w}_L$) is very small compared to the length of $ \textbf {f}_L$ this new function can not contribute much to the reduction of the sum of squares of residuals. The test consists then in calculating the angle $ \theta $ between the two vectors $ \textbf {w}_L$ and $ \textbf {f}_L$ (see also figure 1) and requiring that it's greater then a threshold value which the user must set (TMultiDimFit::SetMinAngle).

Figure 1: (a) Angle $ \theta $ between $ \textbf {w}_l$ and $ \textbf {f}_L$, (b) angle $ \phi $ between $ \textbf {w}_L$ and $ \textbf {D}$
\begin{figure}\begin{center} \begin{tabular}{p{.4\textwidth}p{.4\textwidth}} \... ... \put(80,100){$\mathbf{D}$} \end{picture} \end{tabular} \end{center}\end{figure}


Test 2

Let $ \textbf {D}$ be the data vector to be fitted. As illustrated in figure 1, the $ L^{\mbox{th}}$ function $ \textbf {w}_L$ will contribute significantly to the reduction of $ S$, if the angle $ \phi^\prime$ between $ \textbf {w}_L$ and $ \textbf {D}$ is smaller than an upper limit $ \phi $, defined by the user (TMultiDimFit::SetMaxAngle)

However, the method automatically readjusts the value of this angle while fitting is in progress, in order to make the selection criteria less and less difficult to be fulfilled. The result is that the functions contributing most to the reduction of $ S$ are chosen first (TMultiDimFit::TestFunction).

In case $ \phi $ isn't defined, an alternative method of performing this second test is used: The $ L^{\mbox{th}}$ function $ \textbf {f}_L$ is accepted if (refer also to equation (13))

$\displaystyle \Delta S_L > \frac{S_{L-1}}{L_{max}-L}$ (14)

where $ S_{L-1}$ is the sum of the $ L-1$ first residuals from the $ L-1$ functions previously accepted; and $ L_{max}$ is the total number of functions allowed in the final expression of the fit (defined by user).

>From this we see, that by restricting $ L_{max}$ -- the number of terms in the final model -- the fit is more difficult to perform, since the above selection criteria is more limiting.

The more coefficients we evaluate, the more the sum of squares of residuals $ S$ will be reduced. We can evaluate $ S$ before inverting $ \mathsf{B}$ as shown below.

Coefficients and Coefficient Errors

Having found a parameterization, that is the $ F_l$'s and $ L$, that minimizes $ S$, we still need to determine the coefficients $ c_l$. However, it's a feature of how we choose the significant functions, that the evaluation of the $ c_l$'s becomes trivial [5]. To derive $ \mathbf{c}$, we first note that equation (4) can be written as

$\displaystyle \mathsf{F} = \mathsf{W}\mathsf{B}$ (15)

where

$\displaystyle b_{ij} = \left\{\begin{array}{rcl} \frac{\mathbf{f}_j \bullet \ma... ...f} & i < j\ 1 & \mbox{if} & i = j\ 0 & \mbox{if} & i > j \end{array}\right.$ (16)

Consequently, $ \mathsf{B}$ is an upper triangle matrix, which can be readily inverted. So we now evaluate

$\displaystyle \mathsf{F}\mathsf{B}^{-1} = \mathsf{W}$ (17)

The model $ \mathsf{W}\mathbf{a}$ can therefore be written as

$\displaystyle (\mathsf{F}\mathsf{B}^{-1})\mathbf{a} = \mathsf{F}(\mathsf{B}^{-1}\mathbf{a}) . $

The original model $ \mathsf{F}\mathbf{c}$ is therefore identical with this if

$\displaystyle \mathbf{c} = \left(\mathsf{B}^{-1}\mathbf{a}\right) = \left[\mathbf{a}^T\left(\mathsf{B}^{-1}\right)^T\right]^T .$ (18)

The reason we use $ \left(\mathsf{B}^{-1}\right)^T$ rather then $ \mathsf{B}^{-1}$ is to save storage, since $ \left(\mathsf{B}^{-1}\right)^T$ can be stored in the same matrix as $ \mathsf{B}$ (TMultiDimFit::MakeCoefficients). The errors in the coefficients is calculated by inverting the curvature matrix of the non-orthogonal functions $ f_{lj}$ [1] (TMultiDimFit::MakeCoefficientErrors).


Considerations

It's important to realize that the training sample should be representive of the problem at hand, in particular along the borders of the region of interest. This is because the algorithm presented here, is a interpolation, rahter then a extrapolation [5].

Also, the independent variables $ x_{i}$ need to be linear independent, since the procedure will perform poorly if they are not [5]. One can find an linear transformation from ones original variables $ \xi_{i}$ to a set of linear independent variables $ x_{i}$, using a Principal Components Analysis (see TPrincipal), and then use the transformed variable as input to this class [5] [6].

H. Wind also outlines a method for parameterising a multidimensional dependence over a multidimensional set of variables. An example of the method from [5], is a follows (please refer to [5] for a full discussion):

  1. Define $ \mathbf{P} = (P_1, \ldots, P_5)$ are the 5 dependent quantities that define a track.
  2. Compute, for $ M$ different values of $ \mathbf{P}$, the tracks through the magnetic field, and determine the corresponding $ \mathbf{x} = (x_1, \ldots, x_N)$.
  3. Use the simulated observations to determine, with a simple approximation, the values of $ \mathbf{P}_j$. We call these values $ \mathbf{P}^\prime_j, j = 1, \ldots, M$.
  4. Determine from $ \mathbf{x}$ a set of at least five relevant coordinates $ \mathbf{x}^\prime$, using contrains, or alternative:
  5. Perform a Principal Component Analysis (using TPrincipal), and use to get a linear transformation $ \mathbf{x} \rightarrow \mathbf{x}^\prime$, so that $ \mathbf{x}^\prime$ are constrained and linear independent.
  6. Perform a Principal Component Analysis on $ Q_i = P_i / P^prime_i i = 1, \ldots, 5$, to get linear indenpendent (among themselves, but not independent of $ \mathbf{x}$) quantities $ \mathbf{Q}^\prime$
  7. For each component $ Q^\prime_i$ make a mutlidimensional fit, using $ \mathbf{x}^\prime$ as the variables, thus determing a set of coefficents $ \mathbf{c}_i$.

To process data, using this parameterisation, do

  1. Test wether the observation $ \mathbf{x}$ within the domain of the parameterization, using the result from the Principal Component Analysis.
  2. Determine $ \mathbf{P}^\prime$ as before.
  3. Detetmine $ \mathbf{x}^\prime$ as before.
  4. Use the result of the fit to determind $ \mathbf{Q}^\prime$.
  5. Transform back to $ \mathbf{P}$ from $ \mathbf{Q}^\prime$, using the result from the Principal Component Analysis.


Testing the parameterization

The class also provides functionality for testing the, over the training sample, found parameterization (TMultiDimFit::Fit). This is done by passing the class a test sample of $ M_t$ tuples of the form $ (\mathbf{x}_{t,j}, D_{t,j}, E_{t,j})$, where $ \mathbf{x}_{t,j}$ are the independent variables, $ D_{t,j}$ the known, dependent quantity, and $ E_{t,j}$ is the square error in $ D_{t,j}$ (TMultiDimFit::AddTestRow).

The parameterization is then evaluated at every $ \mathbf{x}_t$ in the test sample, and

$\displaystyle S_t \equiv \sum_{j=1}^{M_t} \left(D_{t,j} - D_p\left(\mathbf{x}_{t,j}\right)\right)^2 $

is evaluated. The relative error over the test sample

$\displaystyle R_t = \frac{S_t}{\sum_{j=1}^{M_t} D_{t,j}^2} $

should not be to low or high compared to $ R$ from the training sample. Also, multiple correlation coefficient from both samples should be fairly close, otherwise one of the samples is not representive of the problem. A large difference in the reduced $ \chi^2$ over the two samples indicate an over fit, and the maximum number of terms in the parameterisation should be reduced.

It's possible to use Minuit [4] to further improve the fit, using the test sample.

Christian Holm
November 2000, NBI

Bibliography

1
Philip R. Bevington and D. Keith Robinson.
Data Reduction and Error Analysis for the Physical Sciences.
McGraw-Hill, 2 edition, 1992.

2
René Brun et al.
Mudifi.
Long writeup DD/75-23, CERN, 1980.

3
Gene H. Golub and Charles F. van Loan.
Matrix Computations.
John Hopkins Univeristy Press, Baltimore, 3 edition, 1996.

4
F. James.
Minuit.
Long writeup D506, CERN, 1998.

5
H. Wind.
Function parameterization.
In Proceedings of the 1972 CERN Computing and Data Processing School, volume 72-21 of Yellow report. CERN, 1972.

6
H. Wind.
1. principal component analysis, 2. pattern recognition for track finding, 3. interpolation and functional representation.
Yellow report EP/81-12, CERN, 1981. 
 */

Function Members (Methods)

public:
TMultiDimFit()
TMultiDimFit(const TMultiDimFit&)
TMultiDimFit(Int_t dimension, TMultiDimFit::EMDFPolyType type = kMonomials, Option_t* option = "")
virtual~TMultiDimFit()
voidTObject::AbstractMethod(const char* method) const
virtual voidAddRow(const Double_t* x, Double_t D, Double_t E = 0)
virtual voidAddTestRow(const Double_t* x, Double_t D, Double_t E = 0)
virtual voidTObject::AppendPad(Option_t* option = "")
virtual voidBrowse(TBrowser* b)
static TClass*Class()
virtual const char*TObject::ClassName() const
virtual voidClear(Option_t* option = "")
virtual TObject*TNamed::Clone(const char* newname = "") const
virtual Int_tTNamed::Compare(const TObject* obj) const
virtual voidTNamed::Copy(TObject& named) const
virtual voidTObject::Delete(Option_t* option = "")
virtual Int_tTObject::DistancetoPrimitive(Int_t px, Int_t py)
virtual voidDraw(Option_t* = "d")
virtual voidTObject::DrawClass() const
virtual TObject*TObject::DrawClone(Option_t* option = "") const
virtual voidTObject::Dump() const
virtual voidTObject::Error(const char* method, const char* msgfmt) const
virtual Double_tEval(const Double_t* x, const Double_t* coeff = 0) const
virtual Double_tEvalError(const Double_t* x, const Double_t* coeff = 0) const
virtual voidTObject::Execute(const char* method, const char* params, Int_t* error = 0)
virtual voidTObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0)
virtual voidTObject::ExecuteEvent(Int_t event, Int_t px, Int_t py)
virtual voidTObject::Fatal(const char* method, const char* msgfmt) const
virtual voidTNamed::FillBuffer(char*& buffer)
virtual TObject*TObject::FindObject(const char* name) const
virtual TObject*TObject::FindObject(const TObject* obj) const
virtual voidFindParameterization(Option_t* option = "")
virtual voidFit(Option_t* option = "")
Double_tGetChi2() const
const TVectorD*GetCoefficients() const
const TMatrixD*GetCorrelationMatrix() const
virtual Option_t*TObject::GetDrawOption() const
static Long_tTObject::GetDtorOnly()
Double_tGetError() const
Int_t*GetFunctionCodes() const
const TMatrixD*GetFunctions() const
virtual TList*GetHistograms() const
virtual const char*TObject::GetIconName() const
Double_tGetMaxAngle() const
Int_tGetMaxFunctions() const
Int_t*GetMaxPowers() const
Double_tGetMaxQuantity() const
Int_tGetMaxStudy() const
Int_tGetMaxTerms() const
const TVectorD*GetMaxVariables() const
Double_tGetMeanQuantity() const
const TVectorD*GetMeanVariables() const
Double_tGetMinAngle() const
Double_tGetMinQuantity() const
Double_tGetMinRelativeError() const
const TVectorD*GetMinVariables() const
virtual const char*TNamed::GetName() const
Int_tGetNCoefficients() const
Int_tGetNVariables() const
virtual char*TObject::GetObjectInfo(Int_t px, Int_t py) const
static Bool_tTObject::GetObjectStat()
virtual Option_t*TObject::GetOption() const
Int_tGetPolyType() const
Int_t*GetPowerIndex() const
Double_tGetPowerLimit() const
const Int_t*GetPowers() const
Double_tGetPrecision() const
const TVectorD*GetQuantity() const
Double_tGetResidualMax() const
Int_tGetResidualMaxRow() const
Double_tGetResidualMin() const
Int_tGetResidualMinRow() const
Double_tGetResidualSumSq() const
Double_tGetRMS() const
Int_tGetSampleSize() const
const TVectorD*GetSqError() const
Double_tGetSumSqAvgQuantity() const
Double_tGetSumSqQuantity() const
Double_tGetTestError() const
Double_tGetTestPrecision() const
const TVectorD*GetTestQuantity() const
Int_tGetTestSampleSize() const
const TVectorD*GetTestSqError() const
const TVectorD*GetTestVariables() const
virtual const char*TNamed::GetTitle() const
virtual UInt_tTObject::GetUniqueID() const
const TVectorD*GetVariables() const
virtual Bool_tTObject::HandleTimer(TTimer* timer)
virtual ULong_tTNamed::Hash() const
virtual voidTObject::Info(const char* method, const char* msgfmt) const
virtual Bool_tTObject::InheritsFrom(const char* classname) const
virtual Bool_tTObject::InheritsFrom(const TClass* cl) const
virtual voidTObject::Inspect() const
static TMultiDimFit*Instance()
voidTObject::InvertBit(UInt_t f)
virtual TClass*IsA() const
virtual Bool_tTObject::IsEqual(const TObject* obj) const
virtual Bool_tIsFolder() const
Bool_tTObject::IsOnHeap() const
virtual Bool_tTNamed::IsSortable() const
Bool_tTObject::IsZombie() const
virtual voidTNamed::ls(Option_t* option = "") const
virtual Double_tMakeChi2(const Double_t* coeff = 0)
virtual voidMakeCode(const char* functionName = "MDF", Option_t* option = "")
virtual voidMakeHistograms(Option_t* option = "A")
virtual voidMakeMethod(const Char_t* className = "MDF", Option_t* option = "")
voidTObject::MayNotUse(const char* method) const
virtual Bool_tTObject::Notify()
static voidTObject::operator delete(void* ptr)
static voidTObject::operator delete(void* ptr, void* vp)
static voidTObject::operator delete[](void* ptr)
static voidTObject::operator delete[](void* ptr, void* vp)
void*TObject::operator new(size_t sz)
void*TObject::operator new(size_t sz, void* vp)
void*TObject::operator new[](size_t sz)
void*TObject::operator new[](size_t sz, void* vp)
TMultiDimFit&operator=(const TMultiDimFit&)
virtual voidTObject::Paint(Option_t* option = "")
virtual voidTObject::Pop()
virtual voidPrint(Option_t* option = "ps") const
virtual Int_tTObject::Read(const char* name)
virtual voidTObject::RecursiveRemove(TObject* obj)
voidTObject::ResetBit(UInt_t f)
virtual voidTObject::SaveAs(const char* filename = "", Option_t* option = "") const
virtual voidTObject::SavePrimitive(ostream& out, Option_t* option = "")
voidSetBinVarX(Int_t nbbinvarx)
voidSetBinVarY(Int_t nbbinvary)
voidTObject::SetBit(UInt_t f)
voidTObject::SetBit(UInt_t f, Bool_t set)
virtual voidTObject::SetDrawOption(Option_t* option = "")
static voidTObject::SetDtorOnly(void* obj)
voidSetMaxAngle(Double_t angle = 0)
voidSetMaxFunctions(Int_t n)
voidSetMaxPowers(const Int_t* powers)
voidSetMaxStudy(Int_t n)
voidSetMaxTerms(Int_t terms)
voidSetMinAngle(Double_t angle = 1)
voidSetMinRelativeError(Double_t error)
virtual voidTNamed::SetName(const char* name)
virtual voidTNamed::SetNameTitle(const char* name, const char* title)
static voidTObject::SetObjectStat(Bool_t stat)
voidSetPowerLimit(Double_t limit = 1e-3)
virtual voidSetPowers(const Int_t* powers, Int_t terms)
virtual voidTNamed::SetTitle(const char* title = "")
virtual voidTObject::SetUniqueID(UInt_t uid)
virtual voidShowMembers(TMemberInspector& insp, char* parent)
virtual Int_tTNamed::Sizeof() const
virtual voidStreamer(TBuffer& b)
voidStreamerNVirtual(TBuffer& b)
virtual voidTObject::SysError(const char* method, const char* msgfmt) const
Bool_tTObject::TestBit(UInt_t f) const
Int_tTObject::TestBits(UInt_t f) const
virtual voidTObject::UseCurrentStyle()
virtual voidTObject::Warning(const char* method, const char* msgfmt) const
virtual Int_tTObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0)
virtual Int_tTObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const
protected:
virtual voidTObject::DoError(int level, const char* location, const char* fmt, va_list va) const
virtual Double_tEvalControl(const Int_t* powers) const
virtual Double_tEvalFactor(Int_t p, Double_t x) const
virtual voidMakeCandidates()
virtual voidMakeCoefficientErrors()
virtual voidMakeCoefficients()
virtual voidMakeCorrelation()
virtual Double_tMakeGramSchmidt(Int_t function)
virtual voidMakeNormalized()
virtual voidMakeParameterization()
virtual voidMakeRealCode(const char* filename, const char* classname, Option_t* option = "")
voidTObject::MakeZombie()
virtual Bool_tSelect(const Int_t* iv)
virtual Bool_tTestFunction(Double_t squareResidual, Double_t dResidur)

Data Members

public:
enum EMDFPolyType { kMonomials
kChebyshev
kLegendre
};
enum TObject::EStatusBits { kCanDelete
kMustCleanup
kObjInCanvas
kIsReferenced
kHasUUID
kCannotPick
kNoContextMenu
kInvalidObject
};
enum TObject::[unnamed] { kIsOnHeap
kNotDeleted
kZombie
kBitMask
kSingleKey
kOverwrite
kWriteDelete
};
protected:
Int_tfBinVarXNumber of bin in independent variables
Int_tfBinVarYNumber of bin in dependent variables
Double_tfChi2Chi square of fit
TVectorDfCoefficientsVector of the final coefficients
TVectorDfCoefficientsRMSVector of RMS of coefficients
Double_tfCorrelationCoeffMulti Correlation coefficient
TMatrixDfCorrelationMatrixCorrelation matrix
Double_tfErrorError from parameterization
TVirtualFitter*fFitter! Fit object (MINUIT)
Int_t*fFunctionCodes[fMaxFunctions] acceptance code
TMatrixDfFunctionsFunctions evaluated over sample
Byte_tfHistogramMaskBit pattern of hisograms used
TList*fHistogramsList of histograms
Bool_tfIsUserFunctionFlag for user defined function
Bool_tfIsVerbose
Double_tfMaxAngleMax angle for acepting new function
Int_tfMaxFuncNVfMaxFunctions*fNVariables
Int_tfMaxFunctionsmax number of functions
Int_t*fMaxPowers[fNVariables] maximum powers
Int_t*fMaxPowersFinal[fNVariables] maximum powers from fit;
Double_tfMaxQuantityMax value of dependent quantity
Double_tfMaxResidualMax redsidual value
Int_tfMaxResidualRowRow giving max residual
Int_tfMaxStudymax functions to study
Int_tfMaxTermsMax terms expected in final expr.
TVectorDfMaxVariablesmax value of independent variables
Double_tfMeanQuantityMean of dependent quantity
TVectorDfMeanVariablesmean value of independent variables
Double_tfMinAngleMin angle for acepting new function
Double_tfMinQuantityMin value of dependent quantity
Double_tfMinRelativeErrorMin relative error accepted
Double_tfMinResidualMin redsidual value
Int_tfMinResidualRowRow giving min residual
TVectorDfMinVariablesmin value of independent variables
Int_tfNCoefficientsDimension of model coefficients
Int_tfNVariablesNumber of independent variables
TStringTNamed::fNameobject identifier
TVectorDfOrthCoefficientsThe model coefficients
TMatrixDfOrthCurvatureMatrixModel matrix
TVectorDfOrthFunctionNormsNorm of the evaluated functions
TMatrixDfOrthFunctionsAs above, but orthogonalised
Int_tfParameterisationCodeExit code of parameterisation
TMultiDimFit::EMDFPolyTypefPolyTypeType of polynomials to use
Int_t*fPowerIndex[fMaxTerms] Index of accepted powers
Double_tfPowerLimitControl parameter
Int_t*fPowers[fMaxFuncNV] where fMaxFuncNV = fMaxFunctions*fNVariables
Double_tfPrecisionRelative precision of param
TVectorDfQuantityTraining sample, dependent quantity
Double_tfRMSRoot mean square of fit
TVectorDfResidualsVector of the final residuals
Int_tfSampleSizeSize of training sample
Bool_tfShowCorrelationprint correlation matrix
TVectorDfSqErrorTraining sample, error in quantity
Double_tfSumSqAvgQuantitySum of squares away from mean
Double_tfSumSqQuantitySumSquare of dependent quantity
Double_tfSumSqResidualSum of Square residuals
Double_tfTestCorrelationCoeffMulti Correlation coefficient
Double_tfTestErrorError from test
Double_tfTestPrecisionRelative precision of test
TVectorDfTestQuantityTest sample, dependent quantity
Int_tfTestSampleSizeSize of test sample
TVectorDfTestSqErrorTest sample, Error in quantity
TVectorDfTestVariablesTest sample, independent variables
TStringTNamed::fTitleobject title
TVectorDfVariablesTraining sample, independent variables
private:
static TMultiDimFit*fgInstanceStatic instance

Class Charts

Inheritance Inherited Members Includes Libraries
Class Charts

Function documentation

TMultiDimFit(const TMultiDimFit& )
 Empty CTOR. Do not use
TMultiDimFit(Int_t dimension, TMultiDimFit::EMDFPolyType type = kMonomials, Option_t* option = "")
 Constructor
 Second argument is the type of polynomials to use in
 parameterisation, one of:
      TMultiDimFit::kMonomials
      TMultiDimFit::kChebyshev
      TMultiDimFit::kLegendre

 Options:
   K      Compute (k)correlation matrix
   V      Be verbose

 Default is no options.
~TMultiDimFit()
 Destructor
void AddRow(const Double_t* x, Double_t D, Double_t E = 0)
 Add a row consisting of fNVariables independent variables, the
 known, dependent quantity, and optionally, the square error in
 the dependent quantity, to the training sample to be used for the
 parameterization.
 The mean of the variables and quantity is calculated on the fly,
 as outlined in TPrincipal::AddRow.
 This sample should be representive of the problem at hand.
 Please note, that if no error is given Poisson statistics is
 assumed and the square error is set to the value of dependent
 quantity.  See also the
class description 




void  AddTestRow(const Double_t* x, Double_t D, Double_t E = 0)


 Add a row consisting of fNVariables independent variables, the
 known, dependent quantity, and optionally, the square error in
 the dependent quantity, to the test sample to be used for the
 test of the parameterization.
 This sample needn't be representive of the problem at hand.
 Please note, that if no error is given Poisson statistics is
 assumed and the square error is set to the value of dependent
 quantity.  See also the
 
class description





void  Browse(TBrowser* b)


 Browse the TMultiDimFit object in the TBrowser.





void  Clear(Option_t* option = "")


 Clear internal structures and variables





Double_t  Eval(const Double_t* x, const Double_t* coeff = 0) const


 Evaluate parameterization at point x. Optional argument coeff is
 a vector of coefficients for the parameterisation, fNCoefficients
 elements long.





Double_t  EvalError(const Double_t* x, const Double_t* coeff = 0) const


 Evaluate parameterization error at point x. Optional argument coeff is
 a vector of coefficients for the parameterisation, fNCoefficients
 elements long.





Double_t  EvalControl(const Int_t* powers) const


 PRIVATE METHOD:
 Calculate the control parameter from the passed powers





Double_t  EvalFactor(Int_t p, Double_t x) const


 PRIVATE METHOD:
 Evaluate function with power p at variable value x





void  FindParameterization(Option_t* option = "")


 Find the parameterization

 Options:
     None so far

 For detailed description of what this entails, please refer to the
 
class description





void  Fit(Option_t* option = "")


 Try to fit the found parameterisation to the test sample.

 Options
     M     use Minuit to improve coefficients

 Also, refer to
 
class description





void  MakeCandidates()


 PRIVATE METHOD:
 Create list of candidate functions for the parameterisation. See
 also
 
class description





Double_t  MakeChi2(const Double_t* coeff = 0)


 Calculate Chi square over either the test sample. The optional
 argument coeff is a vector of coefficients to use in the
 evaluation of the parameterisation. If coeff == 0, then the found
 coefficients is used.
 Used my MINUIT for fit (see TMultDimFit::Fit)





void  MakeCode(const char* functionName = "MDF", Option_t* option = "")


 Generate the file <filename> with .C appended if argument doesn't
 end in .cxx or .C. The contains the implementation of the
 function:

   Double_t <funcname>(Double_t *x)

 which does the same as TMultiDimFit::Eval. Please refer to this
 method.

 Further, the static variables:

     Int_t    gNVariables
     Int_t    gNCoefficients
     Double_t gDMean
     Double_t gXMean[]
     Double_t gXMin[]
     Double_t gXMax[]
     Double_t gCoefficient[]
     Int_t    gPower[]

 are initialized. The only ROOT header file needed is Rtypes.h

 See TMultiDimFit::MakeRealCode for a list of options





void  MakeCoefficientErrors()


 PRIVATE METHOD:
 Compute the errors on the coefficients. For this to be done, the
 curvature matrix of the non-orthogonal functions, is computed.





void  MakeCoefficients()


 PRIVATE METHOD:
 Invert the model matrix B, and compute final coefficients. For a
 more thorough discussion of what this means, please refer to the
 
class description


 First we invert the lower triangle matrix fOrthCurvatureMatrix
 and store the inverted matrix in the upper triangle.





void  MakeCorrelation()


 PRIVATE METHOD:
 Compute the correlation matrix





Double_t  MakeGramSchmidt(Int_t function)


 PRIVATE METHOD:
 Make Gram-Schmidt orthogonalisation. The class description gives
 a thorough account of this algorithm, as well as
 references. Please refer to the
 
class description





void  MakeHistograms(Option_t* option = "A")


 Make histograms of the result of the analysis. This message
 should be sent after having read all data points, but before
 finding the parameterization

 Options:
     A         All the below
     X         Original independent variables
     D         Original dependent variables
     N         Normalised independent variables
     S         Shifted dependent variables
     R1        Residuals versus normalised independent variables
     R2        Residuals versus dependent variable
     R3        Residuals computed on training sample
     R4        Residuals computed on test sample

 For a description of these quantities, refer to
 
class description





void  MakeMethod(const Char_t* className = "MDF", Option_t* option = "")


 Generate the file <classname>MDF.cxx which contains the
 implementation of the method:

   Double_t <classname>::MDF(Double_t *x)

 which does the same as  TMultiDimFit::Eval. Please refer to this
 method.

 Further, the public static members:

   Int_t    <classname>::fgNVariables
   Int_t    <classname>::fgNCoefficients
   Double_t <classname>::fgDMean
   Double_t <classname>::fgXMean[]       //[fgNVariables]
   Double_t <classname>::fgXMin[]        //[fgNVariables]
   Double_t <classname>::fgXMax[]        //[fgNVariables]
   Double_t <classname>::fgCoefficient[] //[fgNCoeffficents]
   Int_t    <classname>::fgPower[]       //[fgNCoeffficents*fgNVariables]

 are initialized, and assumed to exist. The class declaration is
 assumed to be in <classname>.h and assumed to be provided by the
 user.

 See TMultiDimFit::MakeRealCode for a list of options

 The minimal class definition is:

   class <classname> {
   public:
     Int_t    <classname>::fgNVariables;     // Number of variables
     Int_t    <classname>::fgNCoefficients;  // Number of terms
     Double_t <classname>::fgDMean;          // Mean from training sample
     Double_t <classname>::fgXMean[];        // Mean from training sample
     Double_t <classname>::fgXMin[];         // Min from training sample
     Double_t <classname>::fgXMax[];         // Max from training sample
     Double_t <classname>::fgCoefficient[];  // Coefficients
     Int_t    <classname>::fgPower[];        // Function powers

     Double_t Eval(Double_t *x);
   };

 Whether the method <classname>::Eval should be static or not, is
 up to the user.





void  MakeNormalized()


 PRIVATE METHOD:
 Normalize data to the interval [-1;1]. This is needed for the
 classes method to work.





void  MakeParameterization()


 PRIVATE METHOD:
 Find the parameterization over the training sample. A full account
 of the algorithm is given in the
 
class description





void  MakeRealCode(const char* filename, const char* classname, Option_t* option = "")


 PRIVATE METHOD:
 This is the method that actually generates the code for the
 evaluation the parameterization on some point.
 It's called by TMultiDimFit::MakeCode and TMultiDimFit::MakeMethod.

 The options are: NONE so far





void  Print(Option_t* option = "ps") const


 Print statistics etc.
 Options are
   P        Parameters
   S        Statistics
   C        Coefficients
   R        Result of parameterisation
   F        Result of fit
   K        Correlation Matrix
   M        Pretty print formula






Bool_t  Select(const Int_t* iv)


 Selection method. User can override this method for specialized
 selection of acceptable functions in fit. Default is to select
 all. This message is sent during the build-up of the function
 candidates table once for each set of powers in
 variables. Notice, that the argument array contains the powers
 PLUS ONE. For example, to De select the function
     f = x1^2 * x2^4 * x3^5,
 this method should return kFALSE if given the argument
     { 3, 4, 6 }





void  SetMaxAngle(Double_t angle = 0)


 Set the max angle (in degrees) between the initial data vector to
 be fitted, and the new candidate function to be included in the
 fit.  By default it is 0, which automatically chooses another
 selection criteria. See also
 
class description





void  SetMinAngle(Double_t angle = 1)


 Set the min angle (in degrees) between a new candidate function
 and the subspace spanned by the previously accepted
 functions. See also
 
class description





void  SetPowers(const Int_t* powers, Int_t terms)


 Define a user function. The input array must be of the form
 (p11, ..., p1N, ... ,pL1, ..., pLN)
 Where N is the dimension of the data sample, L is the number of
 terms (given in terms) and the first number, labels the term, the
 second the variable.  More information is given in the
 
class description





void  SetPowerLimit(Double_t limit = 1e-3)


 Set the user parameter for the function selection. The bigger the
 limit, the more functions are used. The meaning of this variable
 is defined in the
 
class description





void  SetMaxPowers(const Int_t* powers)


 Set the maximum power to be considered in the fit for each
 variable. See also
 
class description





void  SetMinRelativeError(Double_t error)


 Set the acceptable relative error for when sum of square
 residuals is considered minimized. For a full account, refer to
 the
 
class description





Bool_t  TestFunction(Double_t squareResidual, Double_t dResidur)


 PRIVATE METHOD:
 Test whether the currently considered function contributes to the
 fit. See also
 
class description





 TMultiDimFit(const TMultiDimFit& )




void Draw(Option_t*  = "d")



{ }






Double_t GetChi2()



{ return fChi2; }






const TMatrixD* GetCorrelationMatrix()



{ return &fCorrelationMatrix; }






const TVectorD* GetCoefficients()



{ return &fCoefficients; }






Double_t GetError()



{ return fError; }






Int_t* GetFunctionCodes()



{ return fFunctionCodes; }






const TMatrixD* GetFunctions()



{ return &fFunctions; }






TList* GetHistograms()



{ return fHistograms; }






Double_t GetMaxAngle()



{ return fMaxAngle; }






Int_t GetMaxFunctions()



{ return fMaxFunctions; }






Int_t* GetMaxPowers()



{ return fMaxPowers; }






Double_t GetMaxQuantity()



{ return fMaxQuantity; }






Int_t GetMaxStudy()



{ return fMaxStudy; }






Int_t GetMaxTerms()



{ return fMaxTerms; }






const TVectorD* GetMaxVariables()



{ return &fMaxVariables; }






Double_t GetMeanQuantity()



{ return fMeanQuantity; }






const TVectorD* GetMeanVariables()



{ return &fMeanVariables; }






Double_t GetMinAngle()



{ return fMinAngle; }






Double_t GetMinQuantity()



{ return fMinQuantity; }






Double_t GetMinRelativeError()



{ return fMinRelativeError; }






const TVectorD* GetMinVariables()



{ return &fMinVariables; }






Int_t GetNVariables()



{ return fNVariables; }






Int_t GetNCoefficients()



{ return fNCoefficients; }






Int_t GetPolyType()



{ return fPolyType; }






Int_t* GetPowerIndex()



{ return fPowerIndex; }






Double_t GetPowerLimit()



{ return fPowerLimit; }






const Int_t* GetPowers()



{ return fPowers; }






Double_t GetPrecision()



{ return fPrecision; }






const TVectorD* GetQuantity()



{ return &fQuantity; }






Double_t GetResidualMax()



{ return fMaxResidual; }






Double_t GetResidualMin()



{ return fMinResidual; }






Int_t GetResidualMaxRow()



{ return fMaxResidualRow; }






Int_t GetResidualMinRow()



{ return fMinResidualRow; }






Double_t GetResidualSumSq()



{ return fSumSqResidual; }






Double_t GetRMS()



{ return fRMS; }






Int_t GetSampleSize()



{ return fSampleSize; }






const TVectorD* GetSqError()



{ return &fSqError; }






Double_t GetSumSqAvgQuantity()



{ return fSumSqAvgQuantity; }






Double_t GetSumSqQuantity()



{ return fSumSqQuantity; }






Double_t GetTestError()



{ return fTestError; }






Double_t GetTestPrecision()



{ return fTestPrecision; }






const TVectorD* GetTestQuantity()



{ return &fTestQuantity; }






Int_t GetTestSampleSize()



{ return fTestSampleSize; }






const TVectorD* GetTestSqError()



{ return &fTestSqError; }






const TVectorD* GetTestVariables()



{ return &fTestVariables; }






const TVectorD* GetVariables()



{ return &fVariables; }






TMultiDimFit* Instance()



{ return fgInstance; }






Bool_t IsFolder()



{ return kTRUE; }






void SetBinVarX(Int_t nbbinvarx)



{fBinVarX = nbbinvarx;}






void SetBinVarY(Int_t nbbinvary)



{fBinVarY = nbbinvary;}






void SetMaxFunctions(Int_t n)



{ fMaxFunctions = n; }






void SetMaxStudy(Int_t n)



{ fMaxStudy  = n; }






void SetMaxTerms(Int_t terms)



{ fMaxTerms = terms; }









Author:  Christian Holm Christensen 07/11/2000

Last update: root/hist:$Name:  $:$Id: TMultiDimFit.cxx,v 1.29 2006/12/12 13:48:14 couet Exp $





This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.