
class TGeoRotation: public TGeoMatrix
Geometrical transformation package.
All geometrical transformations handled by the modeller are provided as a
built-in package. This was designed to minimize memory requirements and
optimize performance of point/vector master-to-local and local-to-master
computation. We need to have in mind that a transformation in TGeo has 2
major use-cases. The first one is for defining the placement of a volume
with respect to its container reference frame. This frame will be called
'master' and the frame of the positioned volume - 'local'. If T is a
transformation used for positioning volume daughters, then:
MASTER = T * LOCAL
Therefore a local-to-master conversion will be performed by using T, while
a master-to-local by using its inverse. The second use case is the computation
of the global transformation of a given object in the geometry. Since the
geometry is built as 'volumes-inside-volumes', this global transformation
represent the pile-up of all local transformations in the corresponding
branch. The conversion from the global reference frame and the given object
is also called master-to-local, but it is handled by the manager class.
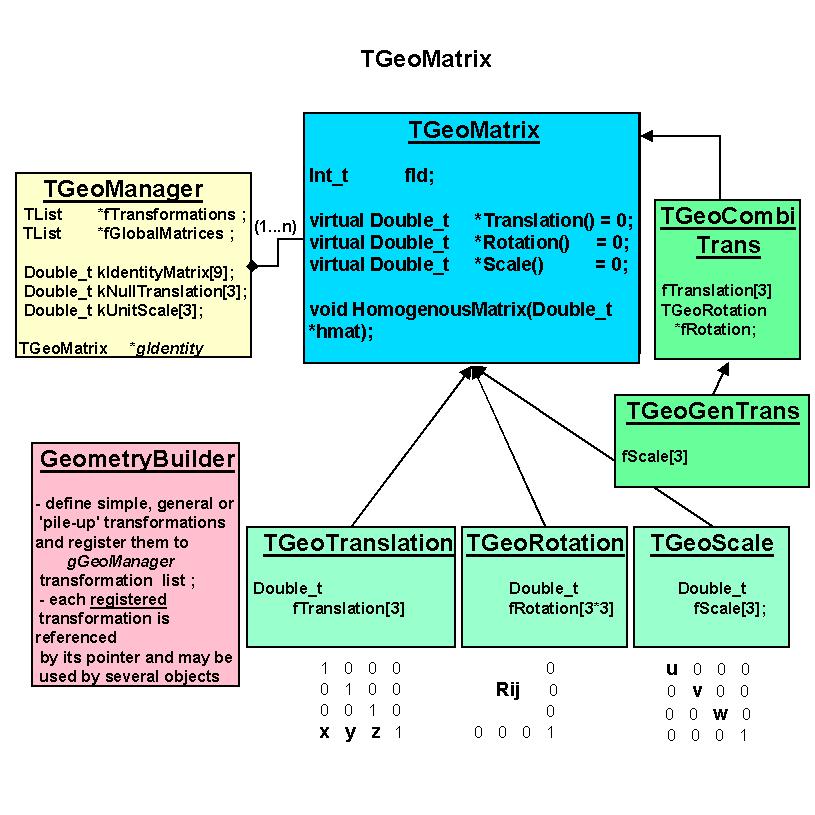
A general homogenous transformation is defined as a 4x4 matrix embeeding
a rotation, a translation and a scale. The advantage of this description
is that each basic transformation can be represented as a homogenous matrix,
composition being performed as simple matrix multiplication.
Rotation: Inverse rotation:
r11 r12 r13 0 r11 r21 r31 0
r21 r22 r23 0 r12 r22 r32 0
r31 r32 r33 0 r13 r23 r33 0
0 0 0 1 0 0 0 1
Translation: Inverse translation:
1 0 0 tx 1 0 0 -tx
0 1 0 ty 0 1 0 -ty
0 0 1 tz 0 0 1 -tz
0 0 0 1 0 0 0 1
Scale: Inverse scale:
sx 0 0 0 1/sx 0 0 0
0 sy 0 0 0 1/sy 0 0
0 0 sz 0 0 0 1/sz 0
0 0 0 1 0 0 0 1
where: rij are the 3x3 rotation matrix components,
tx, ty, tz are the translation components
sx, sy, sz are arbitrary scale constants on the eacks axis,
The disadvantage in using this approach is that computation for 4x4 matrices
is expensive. Even combining two translation would become a multiplication
of their corresponding matrices, which is quite an undesired effect. On the
other hand, it is not a good idea to store a translation as a block of 16
numbers. We have therefore chosen to implement each basic transformation type
as a class deriving from the same basic abstract class and handling its specific
data and point/vector transformation algorithms.
/*
 */
*/
The base class TGeoMatrix defines abstract metods for: - translation, rotation and scale getters. Every derived class stores only its specific data, e.g. a translation stores an array of 3 doubles and a rotation an array of 9. However, asking which is the rotation array of a TGeoTranslation through the base TGeoMatrix interface is a legal operation. The answer in this case is a pointer to a global constant array representing an identity rotation. Double_t *TGeoMatrix::GetTranslation() Double_t *TGeoMatrix::GetRotation() Double_t *TGeoMatrix::GetScale() - MasterToLocal() and LocalToMaster() point and vector transformations : void TGeoMatrix::MasterToLocal(const Double_t *master, Double_t *local) void TGeoMatrix::LocalToMaster(const Double_t *local, Double_t *master) void TGeoMatrix::MasterToLocalVect(const Double_t *master, Double_t *local) void TGeoMatrix::LocalToMasterVect(const Double_t *local, Double_t *master) These allow correct conversion also for reflections. - Transformation type getters : Bool_t TGeoMatrix::IsIdentity() Bool_t TGeoMatrix::IsTranslation() Bool_t TGeoMatrix::IsRotation() Bool_t TGeoMatrix::IsScale() Bool_t TGeoMatrix::IsCombi() (translation + rotation) Bool_t TGeoMatrix::IsGeneral() (translation + rotation + scale) Combinations of basic transformations are represented by specific classes deriving from TGeoMatrix. In order to define a matrix as a combination of several others, a special class TGeoHMatrix is provided. Here is an example of matrix creation : Matrix creation example: root[0] TGeoRotation r1,r2; r1.SetAngles(90,0,30); // rotation defined by Euler angles r2.SetAngles(90,90,90,180,0,0); // rotation defined by GEANT3 angles TGeoTranslation t1(-10,10,0); TGeoTranslation t2(10,-10,5); TGeoCombiTrans c1(t1,r1); TGeoCombiTrans c2(t2,r2); TGeoHMatrix h = c1 * c2; // composition is done via TGeoHMatrix class root[7] TGeoHMatrix *ph = new TGeoHMatrix(hm); // this is the one we want to // use for positioning a volume root[8] ph->Print(); pVolume->AddNode(pVolDaughter,id,ph) // now ph is owned by the manager Rule for matrix creation: - unless explicitly used for positioning nodes (TGeoVolume::AddNode()) all matrices deletion have to be managed by users. Matrices passed to geometry have to be created by using new() operator and their deletion is done by TGeoManager class. Available geometrical transformations 1. TGeoTranslation - represent a (dx,dy,dz) translation. Data members: Double_t fTranslation[3]. Translations can be added/subtracted. TGeoTranslation t1; t1->SetTranslation(-5,10,4); TGeoTranslation *t2 = new TGeoTranslation(4,3,10); t2->Subtract(&t1); 2. Rotations - represent a pure rotation. Data members: Double_t fRotationMatrix[3*3]. Rotations can be defined either by Euler angles, either, by GEANT3 angles : TGeoRotation *r1 = new TGeoRotation(); r1->SetAngles(phi, theta, psi); // all angles in degrees This represent the composition of : first a rotation about Z axis with angle phi, then a rotation with theta about the rotated X axis, and finally a rotation with psi about the new Z axis. r1->SetAngles(th1,phi1, th2,phi2, th3,phi3) This is a rotation defined in GEANT3 style. Theta and phi are the spherical angles of each axis of the rotated coordinate system with respect to the initial one. This construction allows definition of malformed rotations, e.g. not orthogonal. A check is performed and an error message is issued in this case. Specific utilities : determinant, inverse. 3. Scale transformations - represent a scale shrinking/enlargement. Data members :Double_t fScale[3]. Not fully implemented yet. 4. Combined transformations - represent a rotation folowed by a translation. Data members: Double_t fTranslation[3], TGeoRotation *fRotation. TGeoRotation *rot = new TGeoRotation("rot",10,20,30); TGeoTranslation trans; TGeoCombiTrans *c1 = new TGeoCombiTrans(trans, rot); TGeoCombiTrans *c2 = new TGeoCombiTrans("somename",10,20,30,rot) 5. TGeoGenTrans - combined transformations including a scale. Not implemented. 6. TGeoIdentity - a generic singleton matrix representing a identity transformation NOTE: identified by the global variable gGeoIdentity.
Function Members (Methods)
public:
| TGeoRotation() | |
| TGeoRotation(const TGeoRotation& other) | |
| TGeoRotation(const TGeoMatrix& other) | |
| TGeoRotation(const char* name) | |
| TGeoRotation(const char* name, Double_t phi, Double_t theta, Double_t psi) | |
| TGeoRotation(const char* name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2, Double_t theta3, Double_t phi3) | |
| virtual | ~TGeoRotation() |
| void | TObject::AbstractMethod(const char* method) const |
| virtual void | TObject::AppendPad(Option_t* option = "") |
| virtual void | TObject::Browse(TBrowser* b) |
| static TClass* | Class() |
| virtual const char* | TObject::ClassName() const |
| virtual void | Clear(Option_t* option = "") |
| virtual TObject* | TNamed::Clone(const char* newname = "") const |
| virtual Int_t | TNamed::Compare(const TObject* obj) const |
| virtual void | TNamed::Copy(TObject& named) const |
| virtual void | TObject::Delete(Option_t* option = "")MENU |
| Double_t | Determinant() const |
| virtual Int_t | TObject::DistancetoPrimitive(Int_t px, Int_t py) |
| virtual void | TObject::Draw(Option_t* option = "") |
| virtual void | TObject::DrawClass() constMENU |
| virtual TObject* | TObject::DrawClone(Option_t* option = "") constMENU |
| virtual void | TObject::Dump() constMENU |
| virtual void | TObject::Error(const char* method, const char* msgfmt) const |
| virtual void | TObject::Execute(const char* method, const char* params, Int_t* error = 0) |
| virtual void | TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0) |
| virtual void | TObject::ExecuteEvent(Int_t event, Int_t px, Int_t py) |
| void | FastRotZ(Double_t* sincos) |
| virtual void | TObject::Fatal(const char* method, const char* msgfmt) const |
| virtual void | TNamed::FillBuffer(char*& buffer) |
| virtual TObject* | TObject::FindObject(const char* name) const |
| virtual TObject* | TObject::FindObject(const TObject* obj) const |
| void | GetAngles(Double_t& phi, Double_t& theta, Double_t& psi) const |
| void | GetAngles(Double_t& theta1, Double_t& phi1, Double_t& theta2, Double_t& phi2, Double_t& theta3, Double_t& phi3) const |
| virtual Int_t | TGeoMatrix::GetByteCount() const |
| virtual Option_t* | TObject::GetDrawOption() const |
| static Long_t | TObject::GetDtorOnly() |
| void | TGeoMatrix::GetHomogenousMatrix(Double_t* hmat) const |
| virtual const char* | TObject::GetIconName() const |
| void | GetInverse(Double_t* invmat) const |
| virtual const char* | TNamed::GetName() const |
| virtual char* | TObject::GetObjectInfo(Int_t px, Int_t py) const |
| static Bool_t | TObject::GetObjectStat() |
| virtual Option_t* | TObject::GetOption() const |
| Double_t | GetPhiRotation(Bool_t fixX = kFALSE) const |
| char* | TGeoMatrix::GetPointerName() const |
| virtual const Double_t* | GetRotationMatrix() const |
| virtual const Double_t* | GetScale() const |
| virtual const char* | TNamed::GetTitle() const |
| virtual const Double_t* | GetTranslation() const |
| virtual UInt_t | TObject::GetUniqueID() const |
| virtual Bool_t | TObject::HandleTimer(TTimer* timer) |
| virtual ULong_t | TNamed::Hash() const |
| virtual void | TObject::Info(const char* method, const char* msgfmt) const |
| virtual Bool_t | TObject::InheritsFrom(const char* classname) const |
| virtual Bool_t | TObject::InheritsFrom(const TClass* cl) const |
| virtual void | TObject::Inspect() constMENU |
| virtual TGeoMatrix& | Inverse() const |
| void | TObject::InvertBit(UInt_t f) |
| virtual TClass* | IsA() const |
| Bool_t | TGeoMatrix::IsCombi() const |
| virtual Bool_t | TObject::IsEqual(const TObject* obj) const |
| virtual Bool_t | TObject::IsFolder() const |
| Bool_t | TGeoMatrix::IsGeneral() const |
| Bool_t | TGeoMatrix::IsIdentity() const |
| Bool_t | TObject::IsOnHeap() const |
| Bool_t | TGeoMatrix::IsReflection() const |
| Bool_t | TGeoMatrix::IsRegistered() const |
| Bool_t | TGeoMatrix::IsRotAboutZ() const |
| Bool_t | TGeoMatrix::IsRotation() const |
| Bool_t | TGeoMatrix::IsScale() const |
| virtual Bool_t | TNamed::IsSortable() const |
| Bool_t | TGeoMatrix::IsTranslation() const |
| Bool_t | IsValid() const |
| Bool_t | TObject::IsZombie() const |
| virtual void | LocalToMaster(const Double_t* local, Double_t* master) const |
| virtual void | LocalToMasterBomb(const Double_t* local, Double_t* master) const |
| virtual void | LocalToMasterVect(const Double_t* local, Double_t* master) const |
| virtual void | TNamed::ls(Option_t* option = "") const |
| virtual TGeoMatrix* | MakeClone() const |
| virtual void | MasterToLocal(const Double_t* master, Double_t* local) const |
| virtual void | MasterToLocalBomb(const Double_t* master, Double_t* local) const |
| virtual void | MasterToLocalVect(const Double_t* master, Double_t* local) const |
| void | TObject::MayNotUse(const char* method) const |
| void | MultiplyBy(TGeoRotation* rot, Bool_t after = kTRUE) |
| static void | TGeoMatrix::Normalize(Double_t* vect) |
| virtual Bool_t | TObject::Notify() |
| static void | TObject::operator delete(void* ptr) |
| static void | TObject::operator delete(void* ptr, void* vp) |
| static void | TObject::operator delete[](void* ptr) |
| static void | TObject::operator delete[](void* ptr, void* vp) |
| void* | TObject::operator new(size_t sz) |
| void* | TObject::operator new(size_t sz, void* vp) |
| void* | TObject::operator new[](size_t sz) |
| void* | TObject::operator new[](size_t sz, void* vp) |
| TGeoMatrix& | TGeoMatrix::operator*(const TGeoMatrix& right) const |
| TGeoRotation& | operator=(const TGeoMatrix& matrix) |
| TGeoRotation& | operator=(const TGeoRotation& other) |
| Bool_t | TGeoMatrix::operator==(const TGeoMatrix& other) const |
| virtual void | TObject::Paint(Option_t* option = "") |
| virtual void | TObject::Pop() |
| virtual void | TGeoMatrix::Print(Option_t* option = "") constMENU |
| virtual Int_t | TObject::Read(const char* name) |
| virtual void | TObject::RecursiveRemove(TObject* obj) |
| virtual void | ReflectX(Bool_t leftside, Bool_t rotonly = kFALSE) |
| virtual void | ReflectY(Bool_t leftside, Bool_t rotonly = kFALSE) |
| virtual void | ReflectZ(Bool_t leftside, Bool_t rotonly = kFALSE) |
| virtual void | TGeoMatrix::RegisterYourself() |
| void | TObject::ResetBit(UInt_t f) |
| virtual void | RotateX(Double_t angle) |
| virtual void | RotateY(Double_t angle) |
| virtual void | RotateZ(Double_t angle) |
| virtual void | TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU |
| virtual void | SavePrimitive(ostream& out, Option_t* option = "") |
| void | SetAngles(Double_t phi, Double_t theta, Double_t psi) |
| void | SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2, Double_t theta3, Double_t phi3) |
| void | TObject::SetBit(UInt_t f) |
| void | TObject::SetBit(UInt_t f, Bool_t set) |
| void | TGeoMatrix::SetDefaultName() |
| virtual void | TObject::SetDrawOption(Option_t* option = "")MENU |
| static void | TObject::SetDtorOnly(void* obj) |
| virtual void | TGeoMatrix::SetDx(Double_t) |
| virtual void | TGeoMatrix::SetDy(Double_t) |
| virtual void | TGeoMatrix::SetDz(Double_t) |
| void | SetMatrix(const Double_t* rot) |
| virtual void | TNamed::SetName(const char* name)MENU |
| virtual void | TNamed::SetNameTitle(const char* name, const char* title) |
| static void | TObject::SetObjectStat(Bool_t stat) |
| void | SetRotation(const TGeoMatrix& other) |
| virtual void | TNamed::SetTitle(const char* title = "")MENU |
| virtual void | TObject::SetUniqueID(UInt_t uid) |
| virtual void | ShowMembers(TMemberInspector& insp, char* parent) |
| virtual Int_t | TNamed::Sizeof() const |
| virtual void | Streamer(TBuffer& b) |
| void | StreamerNVirtual(TBuffer& b) |
| virtual void | TObject::SysError(const char* method, const char* msgfmt) const |
| Bool_t | TObject::TestBit(UInt_t f) const |
| Int_t | TObject::TestBits(UInt_t f) const |
| virtual void | TObject::UseCurrentStyle() |
| virtual void | TObject::Warning(const char* method, const char* msgfmt) const |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const |
protected:
| void | CheckMatrix() |
| virtual void | TObject::DoError(int level, const char* location, const char* fmt, va_list va) const |
| void | TObject::MakeZombie() |
Data Members
public:
| enum TGeoMatrix::EGeoTransfTypes { | kGeoIdentity | |
| kGeoTranslation | ||
| kGeoRotation | ||
| kGeoScale | ||
| kGeoReflection | ||
| kGeoRegistered | ||
| kGeoSavePrimitive | ||
| kGeoMatrixOwned | ||
| kGeoCombiTrans | ||
| kGeoGenTrans | ||
| }; | ||
| enum TObject::EStatusBits { | kCanDelete | |
| kMustCleanup | ||
| kObjInCanvas | ||
| kIsReferenced | ||
| kHasUUID | ||
| kCannotPick | ||
| kNoContextMenu | ||
| kInvalidObject | ||
| }; | ||
| enum TObject::[unnamed] { | kIsOnHeap | |
| kNotDeleted | ||
| kZombie | ||
| kBitMask | ||
| kSingleKey | ||
| kOverwrite | ||
| kWriteDelete | ||
| }; |
protected:
| TString | TNamed::fName | object identifier |
| Double_t | fRotationMatrix[9] | rotation matrix |
| TString | TNamed::fTitle | object title |
Class Charts
Function documentation
TGeoRotation(const char* name, Double_t phi, Double_t theta, Double_t psi)
Default rotation constructor with Euler angles. Phi is the rotation angle about Z axis and is done first, theta is the rotation about new Y and is done second, psi is the rotation angle about new Z and is done third. All angles are in degrees.
TGeoRotation(const char* name, Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2, Double_t theta3, Double_t phi3)
Rotation constructor a la GEANT3. Angles theta(i), phi(i) are the polar and azimuthal
angles of the (i) axis of the rotated system with respect to the initial non-rotated
system.
Example : the identity matrix (no rotation) is composed by
theta1=90, phi1=0, theta2=90, phi2=90, theta3=0, phi3=0
SetBit(kGeoRotation);
void FastRotZ(Double_t* sincos)
Perform a rotation about Z having the sine/cosine of the rotation angle.
Double_t GetPhiRotation(Bool_t fixX = kFALSE) const
--- Returns rotation angle about Z axis in degrees. If the rotation is a pure
rotation about Z, fixX parameter does not matter, otherwise its meaning is:
- fixX = true : result is the phi angle of the projection of the rotated X axis in the un-rotated XY
- fixX = false : result is the phi angle of the projection of the rotated Y axis - 90 degrees
void LocalToMaster(const Double_t* local, Double_t* master) const
convert a point by multiplying its column vector (x, y, z, 1) to matrix inverse
void MasterToLocal(const Double_t* master, Double_t* local) const
convert a point by multiplying its column vector (x, y, z, 1) to matrix
void RotateX(Double_t angle)
Rotate about X axis of the master frame with angle expressed in degrees.
void RotateY(Double_t angle)
Rotate about Y axis of the master frame with angle expressed in degrees.
void RotateZ(Double_t angle)
Rotate about Z axis of the master frame with angle expressed in degrees.
void SavePrimitive(ostream& out, Option_t* option = "")
Save a primitive as a C++ statement(s) on output stream "out".
void SetAngles(Double_t phi, Double_t theta, Double_t psi)
Set matrix elements according to Euler angles
void SetAngles(Double_t theta1, Double_t phi1, Double_t theta2, Double_t phi2, Double_t theta3, Double_t phi3)
Set matrix elements in the GEANT3 way
void GetAngles(Double_t& theta1, Double_t& phi1, Double_t& theta2, Double_t& phi2, Double_t& theta3, Double_t& phi3) const
Retreive rotation angles
void CheckMatrix()
performes an orthogonality check and finds if the matrix is a reflection Warning("CheckMatrix", "orthogonality check not performed yet");
void GetInverse(Double_t* invmat) const
Get the inverse rotation matrix (which is simply the transpose)
void MultiplyBy(TGeoRotation* rot, Bool_t after = kTRUE)
Multiply this rotation with the one specified by ROT. - after=TRUE (default): THIS*ROT - after=FALSE : ROT*THIS
TGeoMatrix& operator=(const TGeoMatrix &matrix)
const Double_t * GetTranslation() const
const Double_t * GetRotationMatrix() const
void LocalToMasterVect(const Double_t* local, Double_t* master) const
void LocalToMasterBomb(const Double_t* local, Double_t* master) const
void MasterToLocalVect(const Double_t* master, Double_t* local) const
void MasterToLocalBomb(const Double_t* master, Double_t* local) const
TGeoTranslation& operator=(const TGeoMatrix &matrix)
void SetMatrix(const Double_t* rot)
{memcpy(&fRotationMatrix[0], rot, 9*sizeof(Double_t));CheckMatrix();}