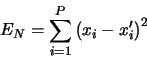class TPrincipal: public TNamed
>
Principal Components Analysis (PCA)
The current implementation is based on the LINTRA package from CERNLIB by R. Brun, H. Hansroul, and J. Kubler. The class has been implemented by Christian Holm Christensen in August 2000.
Introduction
In many applications of various fields of research, the treatment of large amounts of data requires powerful techniques capable of rapid data reduction and analysis. Usually, the quantities most conveniently measured by the experimentalist, are not necessarily the most significant for classification and analysis of the data. It is then useful to have a way of selecting an optimal set of variables necessary for the recognition process and reducing the dimensionality of the problem, resulting in an easier classification procedure.
This paper describes the implementation of one such method of feature selection, namely the principal components analysis. This multidimensional technique is well known in the field of pattern recognition and and its use in Particle Physics has been documented elsewhere (cf. H. Wind, Function Parameterization, CERN 72-21).
Overview
Suppose we have prototypes which are trajectories of particles,
passing through a spectrometer. If one measures the passage of the
particle at say 8 fixed planes, the trajectory is described by an
8-component vector:
in 8-dimensional pattern space.
One proceeds by generating a a representative tracks sample and
building up the covariance matrix ![]() . Its eigenvectors and
eigenvalues are computed by standard methods, and thus a new basis is
obtained for the original 8-dimensional space the expansion of the
prototypes,
. Its eigenvectors and
eigenvalues are computed by standard methods, and thus a new basis is
obtained for the original 8-dimensional space the expansion of the
prototypes,

allows the study of the behavior of the coefficients ![]() for all
the tracks of the sample. The eigenvectors which are insignificant for
the trajectory description in the expansion will have their
corresponding coefficients
for all
the tracks of the sample. The eigenvectors which are insignificant for
the trajectory description in the expansion will have their
corresponding coefficients ![]() close to zero for all the
prototypes.
close to zero for all the
prototypes.
On one hand, a reduction of the dimensionality is then obtained by omitting these least significant vectors in the subsequent analysis.
On the other hand, in the analysis of real data, these least significant variables(?) can be used for the pattern recognition problem of extracting the valid combinations of coordinates describing a true trajectory from the set of all possible wrong combinations.
The program described here performs this principal components analysis
on a sample of data provided by the user. It computes the covariance
matrix, its eigenvalues ands corresponding eigenvectors and exhibits
the behavior of the principal components (![]() ), thus providing
to the user all the means of understanding his data.
), thus providing
to the user all the means of understanding his data.
A short outline of the method of Principal Components is given in subsection 1.3.
Principal Components Method
Let's consider a sample of ![]() prototypes each being characterized by
prototypes each being characterized by
![]() variables
variables
![]() . Each prototype is a point, or a
column vector, in a
. Each prototype is a point, or a
column vector, in a ![]() -dimensional pattern space.
-dimensional pattern space.
![\begin{displaymath}
\mathbf{x} = \left[\begin{array}{c}
x_0\\ x_1\\ \vdots\\ x_{P-1}\end{array}\right]\,,
\end{displaymath}](gif/principal_img8.gif) |
(1) |
Those ![]() variables are the quantities accessible to the
experimentalist, but are not necessarily the most significant for the
classification purpose.
variables are the quantities accessible to the
experimentalist, but are not necessarily the most significant for the
classification purpose.
The Principal Components Method consists of applying a linear transformation to the original variables. This transformation is described by an orthogonal matrix and is equivalent to a rotation of the original pattern space into a new set of coordinate vectors, which hopefully provide easier feature identification and dimensionality reduction.
Let's define the covariance matrix:
This matrix ![]() is real, positive definite, symmetric, and will
have all its eigenvalues greater then zero. It will now be show that
among the family of all the complete orthonormal bases of the pattern
space, the base formed by the eigenvectors of the covariance matrix
and belonging to the largest eigenvalues, corresponds to the most
significant features of the description of the original prototypes.
is real, positive definite, symmetric, and will
have all its eigenvalues greater then zero. It will now be show that
among the family of all the complete orthonormal bases of the pattern
space, the base formed by the eigenvectors of the covariance matrix
and belonging to the largest eigenvalues, corresponds to the most
significant features of the description of the original prototypes.
let the prototypes be expanded on into a set of ![]() basis vectors
basis vectors
![]() ,
,
The `best' feature coordinates ![]() , spanning a feature
space, will be obtained by minimizing the error due to this
truncated expansion, i.e.,
, spanning a feature
space, will be obtained by minimizing the error due to this
truncated expansion, i.e.,
Multiplying (3) by
![]() using (5),
we get
using (5),
we get
The minimization of the sum in (7) is obtained when each
term
![]() is minimum, since
is minimum, since ![]() is
positive definite. By the method of Lagrange multipliers, and the
condition (5), we get
is
positive definite. By the method of Lagrange multipliers, and the
condition (5), we get
which shows that
where
The transformation matrix to go from the pattern space to the feature
space consists of the ordered eigenvectors
![]() for its columns
for its columns
August 2000, CERN
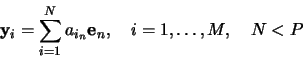
![\begin{displaymath}
\min\left(E_N\right) =
\min\left[\left\langle\left(\mathb...
...\sum^N_{i=0} a_{i_n} \mathbf{e}_n\right)^2\right\rangle\right]
\end{displaymath}](gif/principal_img16.gif)
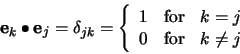
![$\displaystyle \left\langle\left[\sum_{n=N+1}^{P-1} a_{i_n}\mathbf{e}_n\right]^2\right\rangle$](gif/principal_img22.gif)
![$\displaystyle \left\langle\left[\sum_{n=N+1}^{P-1} \mathbf{y}_i^T\bullet\mathbf{e}_n\mathbf{e}_n\right]^2\right\rangle$](gif/principal_img23.gif)

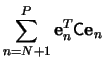

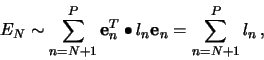
![\begin{displaymath}
\mathsf{T} = \left[
\begin{array}{cccc}
\mathbf{e}_0 &
\...
...bf{e}_{1_{P-1}} & \cdots & \mathbf{e}_{{P-1}_{P-1}}\\
\end{array}\right]
\end{displaymath}](gif/principal_img35.gif)