

Use TProfiles with RDataFrame.
This tutorial illustrates how to use TProfiles in combination with the RDataFrame. See the documentation of TProfile and TProfile2D to better understand the analogy of this code with the example one.

{
.Define("pz", [](double px, double py) { return sqrt(px * px + py * py); }, {"px", "py"})
}
void df003_profiles()
{
auto fileName = "df003_profiles.root";
auto hprof1d =
d.Profile1D({
"hprof1d",
"Profile of py versus px", 64, -4, 4},
"px",
"py");
d.Profile2D({
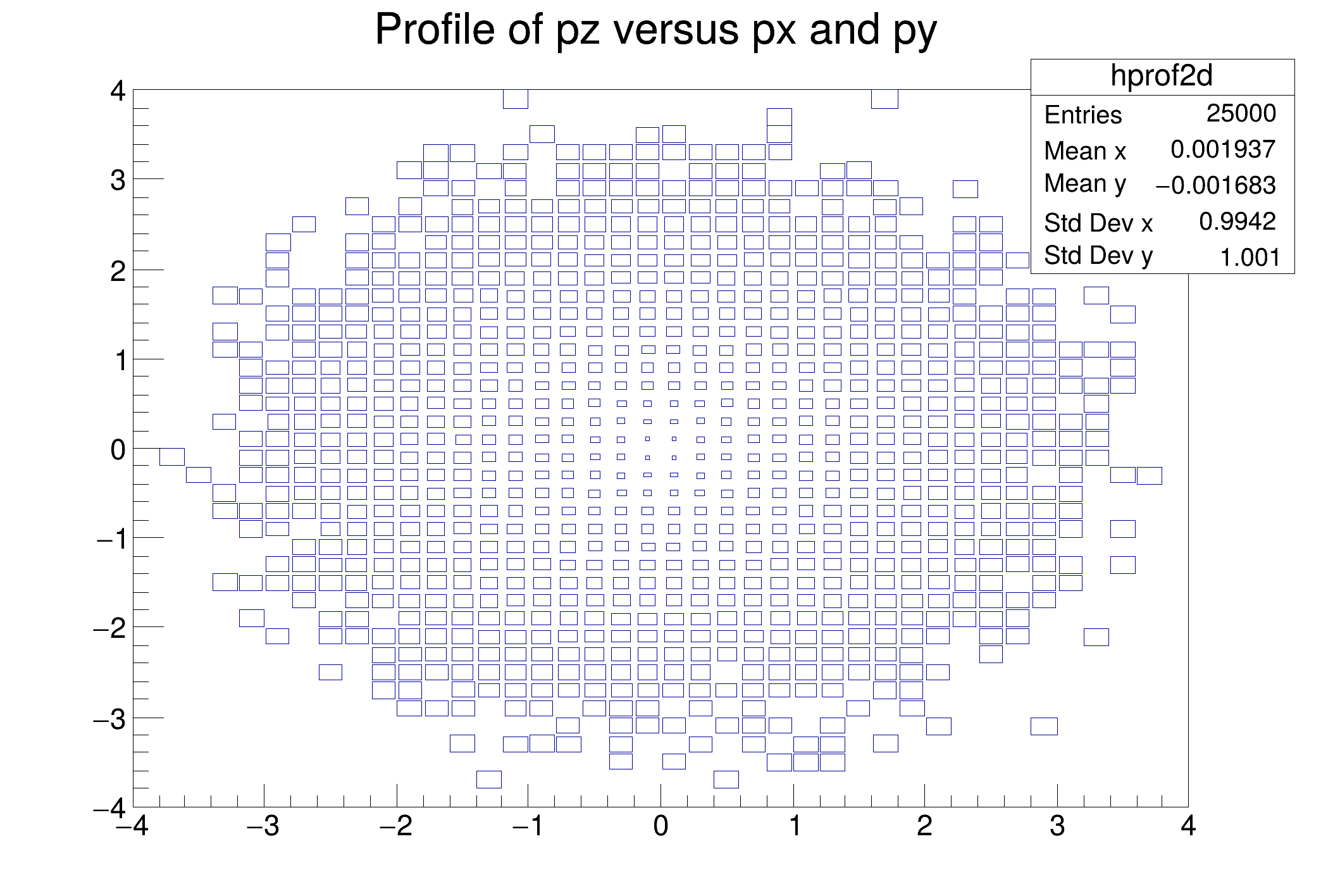
"hprof2d",
"Profile of pz versus px and py", 40, -4, 4, 40, -4, 4, 0, 20},
"px",
"py",
"pz");
auto c1 =
new TCanvas(
"c1",
"Profile histogram example", 200, 10, 700, 500);
auto c2 =
new TCanvas(
"c2",
"Profile2D histogram example", 200, 10, 700, 500);
}
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
R__EXTERN TRandom * gRandom
ROOT's RDataFrame offers a modern, high-level interface for analysis of data stored in TTree ,...
virtual Double_t Gaus(Double_t mean=0, Double_t sigma=1)
Samples a random number from the standard Normal (Gaussian) Distribution with the given mean and sigm...
- Date
- February 2017
- Author
- Danilo Piparo (CERN)
Definition in file df003_profiles.C.



