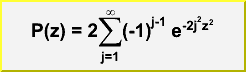TMath
namespace description - header file - source file
public:
Short_t Abs(Short_t d)
Int_t Abs(Int_t d)
Long_t Abs(Long_t d)
Long64_t Abs(Long64_t d)
Float_t Abs(Float_t d)
Double_t Abs(Double_t d)
Double_t ACos(Double_t x)
Double_t ACosH(Double_t)
Double_t ASin(Double_t x)
Double_t ASinH(Double_t)
Double_t ATan(Double_t x)
Double_t ATan2(Double_t y, Double_t x)
Double_t ATanH(Double_t)
Double_t BesselI(Int_t n, Double_t x)
Double_t BesselI0(Double_t x)
Double_t BesselI1(Double_t x)
Double_t BesselJ0(Double_t x)
Double_t BesselJ1(Double_t x)
Double_t BesselK(Int_t n, Double_t x)
Double_t BesselK0(Double_t x)
Double_t BesselK1(Double_t x)
Double_t BesselY0(Double_t x)
Double_t BesselY1(Double_t x)
Double_t Beta(Double_t p, Double_t q)
Double_t BetaCf(Double_t x, Double_t a, Double_t b)
Double_t BetaDist(Double_t x, Double_t p, Double_t q)
Double_t BetaDistI(Double_t x, Double_t p, Double_t q)
Double_t BetaIncomplete(Double_t x, Double_t a, Double_t b)
Long64_t BinarySearch(Long64_t n, const Short_t* array, Short_t value)
Long64_t BinarySearch(Long64_t n, const Short_t** array, Short_t value)
Long64_t BinarySearch(Long64_t n, const Int_t* array, Int_t value)
Long64_t BinarySearch(Long64_t n, const Int_t** array, Int_t value)
Long64_t BinarySearch(Long64_t n, const Float_t* array, Float_t value)
Long64_t BinarySearch(Long64_t n, const Float_t** array, Float_t value)
Long64_t BinarySearch(Long64_t n, const Double_t* array, Double_t value)
Long64_t BinarySearch(Long64_t n, const Double_t** array, Double_t value)
Long64_t BinarySearch(Long64_t n, const Long_t* array, Long_t value)
Long64_t BinarySearch(Long64_t n, const Long_t** array, Long_t value)
Long64_t BinarySearch(Long64_t n, const Long64_t* array, Long64_t value)
Long64_t BinarySearch(Long64_t n, const Long64_t** array, Long64_t value)
Double_t Binomial(Int_t n, Int_t k)
Double_t BinomialI(Double_t p, Int_t n, Int_t k)
Double_t BreitWigner(Double_t x, Double_t mean = 0, Double_t gamma = 1)
void BubbleHigh(Int_t Narr, Double_t* arr1, Int_t* arr2)
void BubbleLow(Int_t Narr, Double_t* arr1, Int_t* arr2)
Double_t C()
Double_t CauchyDist(Double_t x, Double_t t = 0, Double_t s = 1)
Double_t Ccgs()
Double_t Ceil(Double_t x)
Int_t CeilNint(Double_t x)
Double_t ChisquareQuantile(Double_t p, Double_t ndf)
Double_t Cos(Double_t x)
Double_t CosH(Double_t x)
Float_t* Cross(const Float_t* v1, const Float_t* v2, Float_t* out)
Double_t* Cross(const Double_t* v1, const Double_t* v2, Double_t* out)
Double_t CUncertainty()
Double_t DegToRad()
Double_t DiLog(Double_t x)
Double_t E()
Double_t Erf(Double_t x)
Double_t Erfc(Double_t x)
Double_t ErfcInverse(Double_t x)
Double_t ErfInverse(Double_t x)
Bool_t Even(Long_t a)
Double_t Exp(Double_t x)
Double_t Factorial(Int_t i)
Double_t FDist(Double_t F, Double_t N, Double_t M)
Double_t FDistI(Double_t F, Double_t N, Double_t M)
Int_t Finite(Double_t x)
Double_t Floor(Double_t x)
Int_t FloorNint(Double_t x)
Double_t Freq(Double_t x)
Double_t G()
Double_t Gamma(Double_t z)
Double_t Gamma(Double_t a, Double_t x)
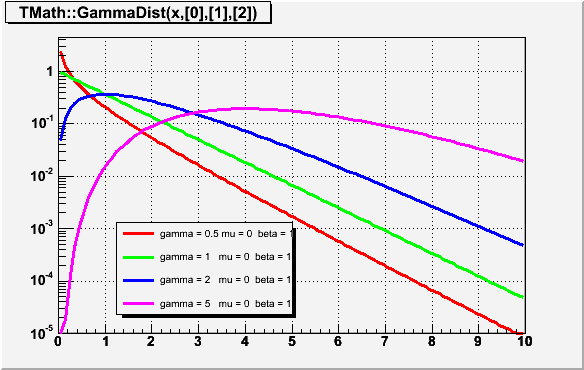
Double_t GammaDist(Double_t x, Double_t gamma, Double_t mu = 0, Double_t beta = 1)
Double_t Gaus(Double_t x, Double_t mean = 0, Double_t sigma = 1, Bool_t norm = kFALSE)
Double_t Gcgs()
Double_t GeomMean(Long64_t n, const Short_t* a)
Double_t GeomMean(Long64_t n, const Int_t* a)
Double_t GeomMean(Long64_t n, const Float_t* a)
Double_t GeomMean(Long64_t n, const Double_t* a)
Double_t GeomMean(Long64_t n, const Long_t* a)
Double_t GeomMean(Long64_t n, const Long64_t* a)
Double_t GhbarC()
Double_t GhbarCUncertainty()
Double_t Gn()
Double_t GnUncertainty()
Double_t GUncertainty()
Double_t H()
ULong_t Hash(const void* txt, Int_t ntxt)
ULong_t Hash(const char* str)
Double_t Hbar()
Double_t Hbarcgs()
Double_t HbarUncertainty()
Double_t HC()
Double_t HCcgs()
Double_t Hcgs()
Double_t HUncertainty()
Double_t Hypot(Double_t x, Double_t y)
Long_t Hypot(Long_t x, Long_t y)
Double_t InvPi()
Bool_t IsInside(Int_t xp, Int_t yp, Int_t np, Int_t* x, Int_t* y)
Bool_t IsInside(Float_t xp, Float_t yp, Int_t np, Float_t* x, Float_t* y)
Bool_t IsInside(Double_t xp, Double_t yp, Int_t np, Double_t* x, Double_t* y)
Int_t IsNaN(Double_t x)
Double_t K()
Double_t Kcgs()
Double_t KolmogorovProb(Double_t z)
Double_t KolmogorovTest(Int_t na, const Double_t* a, Int_t nb, const Double_t* b, Option_t* option)
Short_t KOrdStat(Long64_t n, const Short_t* a, Long64_t k, Long64_t* work = 0)
Int_t KOrdStat(Long64_t n, const Int_t* a, Long64_t k, Long64_t* work = 0)
Float_t KOrdStat(Long64_t n, const Float_t* a, Long64_t k, Long64_t* work = 0)
Double_t KOrdStat(Long64_t n, const Double_t* a, Long64_t k, Long64_t* work = 0)
Double_t KOrdStat(Long64_t n, const Double_t* a, Long64_t k, Int_t* work)
Long64_t KOrdStat(Long64_t n, const Long_t* a, Long64_t k, Long64_t* work = 0)
Long64_t KOrdStat(Long64_t n, const Long64_t* a, Long64_t k, Long64_t* work = 0)
Double_t KUncertainty()
Double_t Landau(Double_t x, Double_t mpv = 0, Double_t sigma = 1, Bool_t norm = kFALSE)
Double_t LandauI(Double_t x)
Double_t LaplaceDist(Double_t x, Double_t alpha = 0, Double_t beta = 1)
Double_t LaplaceDistI(Double_t x, Double_t alpha = 0, Double_t beta = 1)
Double_t Ldexp(Double_t x, Int_t exp)
Double_t Ln10()
Double_t LnGamma(Double_t z)
Long64_t LocMax(Long64_t n, const Short_t* a)
Long64_t LocMax(Long64_t n, const Int_t* a)
Long64_t LocMax(Long64_t n, const Float_t* a)
Long64_t LocMax(Long64_t n, const Double_t* a)
Long64_t LocMax(Long64_t n, const Long_t* a)
Long64_t LocMax(Long64_t n, const Long64_t* a)
Long64_t LocMin(Long64_t n, const Short_t* a)
Long64_t LocMin(Long64_t n, const Int_t* a)
Long64_t LocMin(Long64_t n, const Float_t* a)
Long64_t LocMin(Long64_t n, const Double_t* a)
Long64_t LocMin(Long64_t n, const Long_t* a)
Long64_t LocMin(Long64_t n, const Long64_t* a)
Double_t Log(Double_t x)
Double_t Log10(Double_t x)
Double_t Log2(Double_t x)
Double_t LogE()
Double_t LogNormal(Double_t x, Double_t sigma, Double_t theta = 0, Double_t m = 1)
Short_t Max(Short_t a, Short_t b)
UShort_t Max(UShort_t a, UShort_t b)
Int_t Max(Int_t a, Int_t b)
UInt_t Max(UInt_t a, UInt_t b)
Long_t Max(Long_t a, Long_t b)
ULong_t Max(ULong_t a, ULong_t b)
Long64_t Max(Long64_t a, Long64_t b)
ULong64_t Max(ULong64_t a, ULong64_t b)
Float_t Max(Float_t a, Float_t b)
Double_t Max(Double_t a, Double_t b)
Short_t MaxElement(Long64_t n, const Short_t* a)
Int_t MaxElement(Long64_t n, const Int_t* a)
Float_t MaxElement(Long64_t n, const Float_t* a)
Double_t MaxElement(Long64_t n, const Double_t* a)
Long_t MaxElement(Long64_t n, const Long_t* a)
Long64_t MaxElement(Long64_t n, const Long64_t* a)
Double_t Mean(Long64_t n, const Short_t* a, const Double_t* w = 0)
Double_t Mean(Long64_t n, const Int_t* a, const Double_t* w = 0)
Double_t Mean(Long64_t n, const Float_t* a, const Double_t* w = 0)
Double_t Mean(Long64_t n, const Double_t* a, const Double_t* w = 0)
Double_t Mean(Long64_t n, const Long_t* a, const Double_t* w = 0)
Double_t Mean(Long64_t n, const Long64_t* a, const Double_t* w = 0)
Double_t Median(Long64_t n, const Short_t* a, const Double_t* w = 0, Long64_t* work = 0)
Double_t Median(Long64_t n, const Int_t* a, const Double_t* w = 0, Long64_t* work = 0)
Double_t Median(Long64_t n, const Float_t* a, const Double_t* w = 0, Long64_t* work = 0)
Double_t Median(Long64_t n, const Double_t* a, const Double_t* w = 0, Long64_t* work = 0)
Double_t Median(Long64_t n, const Long_t* a, const Double_t* w = 0, Long64_t* work = 0)
Double_t Median(Long64_t n, const Long64_t* a, const Double_t* w = 0, Long64_t* work = 0)
Short_t Min(Short_t a, Short_t b)
UShort_t Min(UShort_t a, UShort_t b)
Int_t Min(Int_t a, Int_t b)
UInt_t Min(UInt_t a, UInt_t b)
Long_t Min(Long_t a, Long_t b)
ULong_t Min(ULong_t a, ULong_t b)
Long64_t Min(Long64_t a, Long64_t b)
ULong64_t Min(ULong64_t a, ULong64_t b)
Float_t Min(Float_t a, Float_t b)
Double_t Min(Double_t a, Double_t b)
Short_t MinElement(Long64_t n, const Short_t* a)
Int_t MinElement(Long64_t n, const Int_t* a)
Float_t MinElement(Long64_t n, const Float_t* a)
Double_t MinElement(Long64_t n, const Double_t* a)
Long_t MinElement(Long64_t n, const Long_t* a)
Long64_t MinElement(Long64_t n, const Long64_t* a)
Double_t MWair()
Double_t Na()
Double_t NaUncertainty()
Long_t NextPrime(Long_t x)
Int_t Nint(Float_t x)
Int_t Nint(Double_t x)
Float_t* Normal2Plane(const Float_t* v1, const Float_t* v2, const Float_t* v3, Float_t* normal)
Double_t* Normal2Plane(const Double_t* v1, const Double_t* v2, const Double_t* v3, Double_t* normal)
Float_t Normalize(Float_t* v)
Double_t Normalize(Double_t* v)
Float_t NormCross(const Float_t* v1, const Float_t* v2, Float_t* out)
Double_t NormCross(const Double_t* v1, const Double_t* v2, Double_t* out)
Double_t NormQuantile(Double_t p)
Bool_t Odd(Long_t a)
Bool_t Permute(Int_t n, Int_t* a)
Double_t Pi()
Double_t PiOver2()
Double_t PiOver4()
Double_t Poisson(Double_t x, Double_t par)
Double_t PoissonI(Double_t x, Double_t par)
Double_t Power(Double_t x, Double_t y)
Double_t Prob(Double_t chi2, Int_t ndf)
Double_t Qe()
Double_t QeUncertainty()
void Quantiles(Int_t n, Int_t nprob, Double_t* x, Double_t* quantiles, Double_t* prob, Bool_t isSorted = kTRUE, Int_t* index = 0, Int_t type = 7)
Double_t R()
Double_t RadToDeg()
Short_t Range(Short_t lb, Short_t ub, Short_t x)
Int_t Range(Int_t lb, Int_t ub, Int_t x)
Long_t Range(Long_t lb, Long_t ub, Long_t x)
ULong_t Range(ULong_t lb, ULong_t ub, ULong_t x)
Double_t Range(Double_t lb, Double_t ub, Double_t x)
Double_t Rgair()
Double_t RMS(Long64_t n, const Short_t* a)
Double_t RMS(Long64_t n, const Int_t* a)
Double_t RMS(Long64_t n, const Float_t* a)
Double_t RMS(Long64_t n, const Double_t* a)
Double_t RMS(Long64_t n, const Long_t* a)
Double_t RMS(Long64_t n, const Long64_t* a)
Bool_t RootsCubic(const Double_t* coef, Double_t& a, Double_t& b, Double_t& c)
Double_t RUncertainty()
Double_t Sigma()
Double_t SigmaUncertainty()
Short_t Sign(Short_t a, Short_t b)
Int_t Sign(Int_t a, Int_t b)
Long_t Sign(Long_t a, Long_t b)
Long64_t Sign(Long64_t a, Long64_t b)
Float_t Sign(Float_t a, Float_t b)
Double_t Sign(Double_t a, Double_t b)
Double_t Sin(Double_t x)
Double_t SinH(Double_t x)
void Sort(Int_t n, const Short_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Int_t n, const Int_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Int_t n, const Float_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Int_t n, const Double_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Int_t n, const Long_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Int_t n, const Long64_t* a, Int_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Short_t* a, Long64_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Int_t* a, Long64_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Float_t* a, Long64_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Double_t* a, Long64_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Long_t* a, Long64_t* index, Bool_t down = kTRUE)
void Sort(Long64_t n, const Long64_t* a, Long64_t* index, Bool_t down = kTRUE)
Double_t Sqrt(Double_t x)
Double_t StruveH0(Double_t x)
Double_t StruveH1(Double_t x)
Double_t StruveL0(Double_t x)
Double_t StruveL1(Double_t x)
Double_t Student(Double_t T, Double_t ndf)
Double_t StudentI(Double_t T, Double_t ndf)
Double_t StudentQuantile(Double_t p, Double_t ndf, Bool_t lower_tail = kTRUE)
Double_t Tan(Double_t x)
Double_t TanH(Double_t x)
Double_t TwoPi()
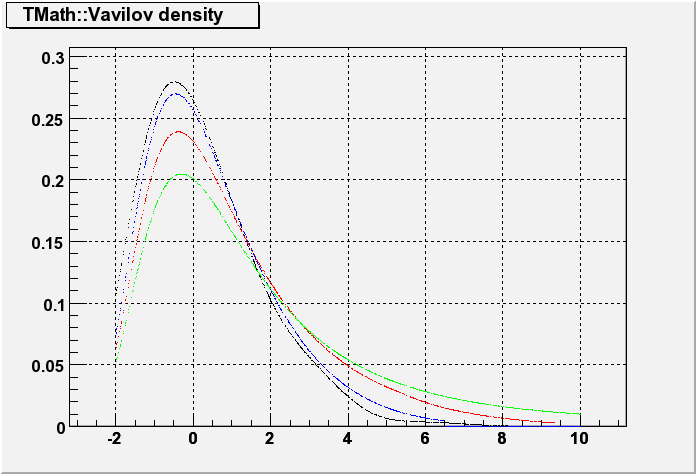
Double_t Vavilov(Double_t x, Double_t kappa, Double_t beta2)
Double_t VavilovI(Double_t x, Double_t kappa, Double_t beta2)
Double_t Voigt(Double_t x, Double_t sigma, Double_t lg, Int_t R = 4)
TMath
Encapsulate math routines.
Long_t NextPrime(Long_t x)
Return next prime number after x, unless x is a prime in which case
x is returned.
Int_t Nint(Float_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Int_t Nint(Double_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Double_t DiLog(Double_t x)
The DiLogarithm function
Code translated by R.Brun from CERNLIB DILOG function C332
Double_t Erf(Double_t x)
Computation of the error function erf(x).
Erf(x) = (2/sqrt(pi)) Integral(exp(-t^2))dt between 0 and x
Double_t Erfc(Double_t x)
Compute the complementary error function erfc(x).
Erfc(x) = (2/sqrt(pi)) Integral(exp(-t^2))dt between x and infinity
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Freq(Double_t x)
Computation of the normal frequency function freq(x).
Freq(x) = (1/sqrt(2pi)) Integral(exp(-t^2/2))dt between -infinity and x.
Translated from CERNLIB C300 by Rene Brun.
Double_t Gamma(Double_t z)
Computation of gamma(z) for all z>0.
C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Gamma(Double_t a,Double_t x)
Computation of the upper incomplete gamma function P(a,x) as defined in the
Handbook of Mathematical Functions by Abramowitz and Stegun, formula 6.5.1 on page 260 .
Note that this is the version of the incomplete gamma function as used in statistics :
its normalization is such that TMath::Gamma(a,+infinity) = 1 .
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t LnGamma(Double_t z)
Computation of ln[gamma(z)] for all z>0.
C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
The accuracy of the result is better than 2e-10.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Normalize(Double_t v[3])
Normalize a vector v in place.
Returns the norm of the original vector.
This implementation (thanks Kevin Lynch <krlynch@bu.edu>) is protected
against possible overflows.
Double_t Poisson(Double_t x, Double_t par)
compute the Poisson distribution function for (x,par)
The Poisson PDF is implemented by means of Euler's Gamma-function
(for the factorial), so for all integer arguments it is correct.
BUT for non-integer values it IS NOT equal to the Poisson distribution.
see TMath::PoissonI to get a non-smooth function.
Note that for large values of par, it is better to call
TMath::Gaus(x,par,sqrt(par),kTRUE)

Double_t Prob(Double_t chi2,Int_t ndf)
Computation of the probability for a certain Chi-squared (chi2)
and number of degrees of freedom (ndf).
Calculations are based on the incomplete gamma function P(a,x),
where a=ndf/2 and x=chi2/2.
P(a,x) represents the probability that the observed Chi-squared
for a correct model should be less than the value chi2.
The returned probability corresponds to 1-P(a,x),
which denotes the probability that an observed Chi-squared exceeds
the value chi2 by chance, even for a correct model.
--- NvE 14-nov-1998 UU-SAP Utrecht
Double_t KolmogorovProb(Double_t z)
Calculates the Kolmogorov distribution function,
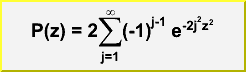
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB.
Double_t KolmogorovTest(Int_t na, const Double_t *a, Int_t nb, const Double_t *b, Option_t *option)
Statistical test whether two one-dimensional sets of points are compatible
with coming from the same parent distribution, using the Kolmogorov test.
That is, it is used to compare two experimental distributions of unbinned data.
Input:
a,b: One-dimensional arrays of length na, nb, respectively.
The elements of a and b must be given in ascending order.
option is a character string to specify options
"D" Put out a line of "Debug" printout
"M" Return the Maximum Kolmogorov distance instead of prob
Output:
The returned value prob is a calculated confidence level which gives a
statistical test for compatibility of a and b.
Values of prob close to zero are taken as indicating a small probability
of compatibility. For two point sets drawn randomly from the same parent
distribution, the value of prob should be uniformly distributed between
zero and one.
in case of error the function return -1
If the 2 sets have a different number of points, the minimum of
the two sets is used.
Method:
The Kolmogorov test is used. The test statistic is the maximum deviation
between the two integrated distribution functions, multiplied by the
normalizing factor (rdmax*sqrt(na*nb/(na+nb)).
Code adapted by Rene Brun from CERNLIB routine TKOLMO (Fred James)
(W.T. Eadie, D. Drijard, F.E. James, M. Roos and B. Sadoulet,
Statistical Methods in Experimental Physics, (North-Holland,
Amsterdam 1971) 269-271)
NOTE1
A good description of the Kolmogorov test can be seen at:
http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm
Double_t Voigt(Double_t xx, Double_t sigma, Double_t lg, Int_t r)
Computation of Voigt function (normalised).
Voigt is a convolution of
gauss(xx) = 1/(sqrt(2*pi)*sigma) * exp(xx*xx/(2*sigma*sigma)
and
lorentz(xx) = (1/pi) * (lg/2) / (xx*xx + g*g/4)
functions.
The Voigt function is known to be the real part of Faddeeva function also
called complex error function [2].
The algoritm was developed by J. Humlicek [1].
This code is based on fortran code presented by R. J. Wells [2].
Translated and adapted by Miha D. Puc
To calculate the Faddeeva function with relative error less than 10^(-r).
r can be set by the the user subject to the constraints 2 <= r <= 5.
[1] J. Humlicek, JQSRT, 21, 437 (1982).
[2] R.J. Wells "Rapid Approximation to the Voigt/Faddeeva Function and its
Derivatives" JQSRT 62 (1999), pp 29-48.
http://www-atm.physics.ox.ac.uk/user/wells/voigt.html
Bool_t RootsCubic(const Double_t coef[4],Double_t &a, Double_t &b, Double_t &c)
Calculates roots of polynomial of 3rd order a*x^3 + b*x^2 + c*x + d, where
a == coef[3], b == coef[2], c == coef[1], d == coef[0]
coef[3] must be different from 0
If the boolean returned by the method is false:
==> there are 3 real roots a,b,c
If the boolean returned by the method is true:
==> there is one real root a and 2 complex conjugates roots (b+i*c,b-i*c)
Author: Francois-Xavier Gentit
Long64_t LocMin(Long64_t n, const Short_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMin(Long64_t n, const Int_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMin(Long64_t n, const Float_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMin(Long64_t n, const Double_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMin(Long64_t n, const Long_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMin(Long64_t n, const Long64_t *a)
Return index of array with the minimum element.
If more than one element is minimum returns first found.
Long64_t LocMax(Long64_t n, const Short_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Long64_t LocMax(Long64_t n, const Int_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Long64_t LocMax(Long64_t n, const Float_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Long64_t LocMax(Long64_t n, const Double_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Long64_t LocMax(Long64_t n, const Long64_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Long64_t LocMax(Long64_t n, const Long_t *a)
Return index of array with the maximum element.
If more than one element is maximum returns first found.
Double_t Median(Long64_t n, const Short_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Long64_t n, const Int_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Long64_t n, const Float_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Long64_t n, const Double_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Long64_t n, const Long_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t Median(Long64_t n, const Long64_t *a, const Double_t *w, Long64_t *work)
Return the median of the array a where each entry i has weight w[i] .
Both arrays have a length of at least n . The median is a number obtained
from the sorted array a through
median = (a[jl]+a[jh])/2. where (using also the sorted index on the array w)
sum_i=0,jl w[i] <= sumTot/2
sum_i=0,jh w[i] >= sumTot/2
sumTot = sum_i=0,n w[i]
If w=0, the algorithm defaults to the median definition where it is
a number that divides the sorted sequence into 2 halves.
When n is odd or n > 1000, the median is kth element k = (n + 1) / 2.
when n is even and n < 1000the median is a mean of the elements k = n/2 and k = n/2 + 1.
If work is supplied, it is used to store the sorting index and assumed to be
>= n . If work=0, local storage is used, either on the stack if n < kWorkMax
or on the heap for n >= kWorkMax .
Double_t KOrdStat(Long64_t n, const Double_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Double_t KOrdStat(Long64_t n, const Double_t *a, Long64_t k, Int_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Float_t KOrdStat(Long64_t n, const Float_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Int_t KOrdStat(Long64_t n, const Int_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Short_t KOrdStat(Long64_t n, const Short_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n . If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Long64_t KOrdStat(Long64_t n, const Long_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
Long64_t KOrdStat(Long64_t n, const Long64_t *a, Long64_t k, Long64_t *work)
Returns k_th order statistic of the array a of size n
(k_th smallest element out of n elements).
C-convention is used for array indexing, so if you want
the second smallest element, call KOrdStat(n, a, 1).
If work is supplied, it is used to store the sorting index and
assumed to be >= n. If work=0, local storage is used, either on
the stack if n < kWorkMax or on the heap for n >= kWorkMax.
void Quantiles(Int_t n, Int_t nprob, Double_t *x, Double_t *quantiles, Double_t *prob, Bool_t isSorted, Int_t *index, Int_t type)
Computes sample quantiles, corresponding to the given probabilities
Parameters:
x -the data sample
n - its size
quantiles - computed quantiles are returned in there
prob - probabilities where to compute quantiles
nprob - size of prob array
isSorted - is the input array x sorted?
NOTE, that when the input is not sorted, an array of integers of size n needs
to be allocated. It can be passed by the user in parameter index,
or, if not passed, it will be allocated inside the function
type - method to compute (from 1 to 9). Following types are provided:
Discontinuous:
type=1 - inverse of the empirical distribution function
type=2 - like type 1, but with averaging at discontinuities
type=3 - SAS definition: nearest even order statistic
Piecwise linear continuous:
In this case, sample quantiles can be obtained by linear interpolation
between the k-th order statistic and p(k).
type=4 - linear interpolation of empirical cdf, p(k)=k/n;
type=5 - a very popular definition, p(k) = (k-0.5)/n;
type=6 - used by Minitab and SPSS, p(k) = k/(n+1);
type=7 - used by S-Plus and R, p(k) = (k-1)/(n-1);
type=8 - resulting sample quantiles are approximately median unbiased
regardless of the distribution of x. p(k) = (k-1/3)/(n+1/3);
type=9 - resulting sample quantiles are approximately unbiased, when
the sample comes from Normal distribution. p(k)=(k-3/8)/(n+1/4);
default type = 7
References:
1) Hyndman, R.J and Fan, Y, (1996) "Sample quantiles in statistical packages"
American Statistician, 50, 361-365
2) R Project documentation for the function quantile of package {stats}
Long64_t BinarySearch(Long64_t n, const Short_t *array, Short_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Short_t **array, Short_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Int_t *array, Int_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Int_t **array, Int_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Float_t *array, Float_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Float_t **array, Float_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Double_t *array, Double_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Double_t **array, Double_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Long_t *array, Long_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Long_t **array, Long_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Long64_t *array, Long64_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Long64_t BinarySearch(Long64_t n, const Long64_t **array, Long64_t value)
Binary search in an array of n values to locate value.
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Bool_t IsInside(Int_t xp, Int_t yp, Int_t np, Int_t *x, Int_t *y)
Function which returns kTRUE if point xp,yp lies inside the
polygon defined by the np points in arrays x and y, kFALSE otherwise
NOTE that the polygon must be a closed polygon (1st and last point
must be identical).
void Sort(Int_t n1, const Short_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Short_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Int_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Int_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Float_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Float_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Double_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Double_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Long_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, const Long64_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Short_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Short_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Int_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Int_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Float_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Float_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Double_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Double_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Long_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Long64_t n1, const Long64_t *a, Long64_t *index, Bool_t down)
Sort the n1 elements of the Long64_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void BubbleHigh(Int_t Narr, Double_t *arr1, Int_t *arr2)
Bubble sort variant to obtain the order of an array's elements into
an index in order to do more useful things than the standard built
in functions.
*arr1 is unchanged;
*arr2 is the array of indicies corresponding to the decending value
of arr1 with arr2[0] corresponding to the largest arr1 value and
arr2[Narr] the smallest.
Author: Adrian Bevan (bevan@slac.stanford.edu)
ULong_t Hash(const void *txt, Int_t ntxt)
Calculates hash index from any char string.
Based on precalculated table of 256 specially selected random numbers.
For string: i = TMath::Hash(string,nstring);
For int: i = TMath::Hash(&intword,sizeof(int));
For pointer: i = TMath::Hash(&pointer,sizeof(void*));
Limitation: for ntxt>256 calculates hash only from first 256 bytes
V.Perev
ULong_t Hash(const void *txt, Int_t ntxt)
Calculates hash index from any char string.
Based on precalculated table of 256 specially selected numbers.
These numbers are selected in such a way, that for string
length == 4 (integer number) the hash is unambigous, i.e.
from hash value we can recalculate input (no degeneration).
The quality of hash method is good enough, that
"random" numbers made as R = Hash(1), Hash(2), ...Hash(N)
tested by <R>, <R*R>, <Ri*Ri+1> gives the same result
as for libc rand().
For string: i = TMath::Hash(string,nstring);
For int: i = TMath::Hash(&intword,sizeof(int));
For pointer: i = TMath::Hash(&pointer,sizeof(void*));
V.Perev
Double_t BesselI0(Double_t x)
Compute the modified Bessel function I_0(x) for any real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK0(Double_t x)
Compute the modified Bessel function K_0(x) for positive real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI1(Double_t x)
Compute the modified Bessel function I_1(x) for any real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK1(Double_t x)
Compute the modified Bessel function K_1(x) for positive real x.
M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK(Int_t n,Double_t x)
Compute the Integer Order Modified Bessel function K_n(x)
for n=0,1,2,... and positive real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI(Int_t n,Double_t x)
Compute the Integer Order Modified Bessel function I_n(x)
for n=0,1,2,... and any real x.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BetaDist(Double_t x, Double_t p, Double_t q)
Computes the probability density function of the Beta distribution
(the distribution function is computed in BetaDistI).
The first argument is the point, where the function will be
computed, second and third are the function parameters.
Since the Beta distribution is bounded on both sides, it's often
used to represent processes with natural lower and upper limits.
Double_t BetaDistI(Double_t x, Double_t p, Double_t q)
Computes the distribution function of the Beta distribution.
The first argument is the point, where the function will be
computed, second and third are the function parameters.
Since the Beta distribution is bounded on both sides, it's often
used to represent processes with natural lower and upper limits.
Double_t BinomialI(Double_t p, Int_t n, Int_t k)
Suppose an event occurs with probability _p_ per trial
Then the probability P of its occuring _k_ or more times
in _n_ trials is termed a cumulative binomial probability
the formula is P = sum_from_j=k_to_n(TMath::Binomial(n, j)*
*TMath::Power(p, j)*TMath::Power(1-p, n-j)
For _n_ larger than 12 BetaIncomplete is a much better way
to evaluate the sum than would be the straightforward sum calculation
for _n_ smaller than 12 either method is acceptable
("Numerical Recipes")
--implementation by Anna Kreshuk
Double_t CauchyDist(Double_t x, Double_t t, Double_t s)
Computes the density of Cauchy distribution at point x
by default, standard Cauchy distribution is used (t=0, s=1)
t is the location parameter
s is the scale parameter
The Cauchy distribution, also called Lorentzian distribution,
is a continuous distribution describing resonance behavior
The mean and standard deviation of the Cauchy distribution are undefined.
The practical meaning of this is that collecting 1,000 data points gives
no more accurate an estimate of the mean and standard deviation than
does a single point.
The formula was taken from "Engineering Statistics Handbook" on site
http://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm
Implementation by Anna Kreshuk.
Example:
TF1* fc = new TF1("fc", "TMath::CauchyDist(x, [0], [1])", -5, 5);
fc->SetParameters(0, 1);
fc->Draw();
Double_t ChisquareQuantile(Double_t p, Double_t ndf)
Evaluate the quantiles of the chi-squared probability distribution function.
Algorithm AS 91 Appl. Statist. (1975) Vol.24, P.35
implemented by Anna Kreshuk.
Incorporates the suggested changes in AS R85 (vol.40(1), pp.233-5, 1991)
Parameters:
p - the probability value, at which the quantile is computed
ndf - number of degrees of freedom
Double_t FDist(Double_t F, Double_t N, Double_t M)
Computes the density function of F-distribution
(probability function, integral of density, is computed in FDistI).
Parameters N and M stand for degrees of freedom of chi-squares
mentioned above parameter F is the actual variable x of the
density function p(x) and the point at which the density function
is calculated.
About F distribution:
F-distribution arises in testing whether two random samples
have the same variance. It is the ratio of two chi-square
distributions, with N and M degrees of freedom respectively,
where each chi-square is first divided by it's number of degrees
of freedom.
Implementation by Anna Kreshuk.
Double_t FDistI(Double_t F, Double_t N, Double_t M)
Calculates the cumulative distribution function of F-distribution,
this function occurs in the statistical test of whether two observed
samples have the same variance. For this test a certain statistic F,
the ratio of observed dispersion of the first sample to that of the
second sample, is calculated. N and M stand for numbers of degrees
of freedom in the samples 1-FDistI() is the significance level at
which the hypothesis "1 has smaller variance than 2" can be rejected.
A small numerical value of 1 - FDistI() implies a very significant
rejection, in turn implying high confidence in the hypothesis
"1 has variance greater than 2".
Implementation by Anna Kreshuk.
Double_t GammaDist(Double_t x, Double_t gamma, Double_t mu, Double_t beta)
Computes the density function of Gamma distribution at point x.
gamma - shape parameter
mu - location parameter
beta - scale parameter
The formula was taken from "Engineering Statistics Handbook" on site
http://www.itl.nist.gov/div898/handbook/eda/section3/eda366b.htm
Implementation by Anna Kreshuk.
Double_t LaplaceDist(Double_t x, Double_t alpha, Double_t beta)
Computes the probability density funciton of Laplace distribution
at point x, with location parameter alpha and shape parameter beta.
By default, alpha=0, beta=1
This distribution is known under different names, most common is
double exponential distribution, but it also appears as
the two-tailed exponential or the bilateral exponential distribution
Double_t LaplaceDistI(Double_t x, Double_t alpha, Double_t beta)
Computes the distribution funciton of Laplace distribution
at point x, with location parameter alpha and shape parameter beta.
By default, alpha=0, beta=1
This distribution is known under different names, most common is
double exponential distribution, but it also appears as
the two-tailed exponential or the bilateral exponential distribution
Double_t LogNormal(Double_t x, Double_t sigma, Double_t theta, Double_t m)
Computes the density of LogNormal distribution at point x.
Variable X has lognormal distribution if Y=Ln(X) has normal distribution
sigma is the shape parameter
theta is the location parameter
m is the scale parameter
The formula was taken from "Engineering Statistics Handbook" on site
http://www.itl.nist.gov/div898/handbook/eda/section3/eda3669.htm
Implementation by Anna Kreshuk.

Double_t NormQuantile(Double_t p)
Computes quantiles for standard normal distribution N(0, 1)
at probability p
ALGORITHM AS241 APPL. STATIST. (1988) VOL. 37, NO. 3, 477-484.
Bool_t Permute(Int_t n, Int_t *a)
Simple recursive algorithm to find the permutations of
n natural numbers, not necessarily all distinct
adapted from CERNLIB routine PERMU.
The input array has to be initialised with a non descending
sequence. The method returns kFALSE when
all combinations are exhausted.
Double_t Student(Double_t T, Double_t ndf)
Computes density function for Student's t- distribution
(the probability function (integral of density) is computed in StudentI).
First parameter stands for x - the actual variable of the
density function p(x) and the point at which the density is calculated.
Second parameter stands for number of degrees of freedom.
About Student distribution:
Student's t-distribution is used for many significance tests, for example,
for the Student's t-tests for the statistical significance of difference
between two sample means and for confidence intervals for the difference
between two population means.
Example: suppose we have a random sample of size n drawn from normal
distribution with mean Mu and st.deviation Sigma. Then the variable
t = (sample_mean - Mu)/(sample_deviation / sqrt(n))
has Student's t-distribution with n-1 degrees of freedom.
NOTE that this function's second argument is number of degrees of freedom,
not the sample size.
As the number of degrees of freedom grows, t-distribution approaches
Normal(0,1) distribution.
Implementation by Anna Kreshuk.
Double_t StudentI(Double_t T, Double_t ndf)
Calculates the cumulative distribution function of Student's
t-distribution second parameter stands for number of degrees of freedom,
not for the number of samples
if x has Student's t-distribution, the function returns the probability of
x being less than T.
Implementation by Anna Kreshuk.
Double_t StudentQuantile(Double_t p, Double_t ndf, Bool_t lower_tail)
Computes quantiles of the Student's t-distribution
1st argument is the probability, at which the quantile is computed
2nd argument - the number of degrees of freedom of the
Student distribution
When the 3rd argument lower_tail is kTRUE (default)-
the algorithm returns such x0, that
P(x < x0)=p
upper tail (lower_tail is kFALSE)- the algorithm returns such x0, that
P(x > x0)=p
the algorithm was taken from
G.W.Hill, "Algorithm 396, Student's t-quantiles"
"Communications of the ACM", 13(10), October 1970
Double_t Vavilov(Double_t x, Double_t kappa, Double_t beta2)
Returns the value of the Vavilov density function
Parameters: 1st - the point were the density function is evaluated
2nd - value of kappa (distribution parameter)
3rd - value of beta2 (distribution parameter)
The algorithm was taken from the CernLib function vavden(G115)
Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution
Nucl.Instr. and Meth. B47(1990), 215-224
Accuracy: quote from the reference above:
"The resuls of our code have been compared with the values of the Vavilov
density function computed numerically in an accurate way: our approximation
shows a difference of less than 3% around the peak of the density function, slowly
increasing going towards the extreme tails to the right and to the left"
Double_t VavilovI(Double_t x, Double_t kappa, Double_t beta2)
Returns the value of the Vavilov distribution function
Parameters: 1st - the point were the density function is evaluated
2nd - value of kappa (distribution parameter)
3rd - value of beta2 (distribution parameter)
The algorithm was taken from the CernLib function vavden(G115)
Reference: A.Rotondi and P.Montagna, Fast Calculation of Vavilov distribution
Nucl.Instr. and Meth. B47(1990), 215-224
Accuracy: quote from the reference above:
"The resuls of our code have been compared with the values of the Vavilov
density function computed numerically in an accurate way: our approximation
shows a difference of less than 3% around the peak of the density function, slowly
increasing going towards the extreme tails to the right and to the left"
Double_t LandauI(Double_t x)
Returns the value of the Landau distribution function at point x.
The algorithm was taken from the Cernlib function dislan(G110)
Reference: K.S.Kolbig and B.Schorr, "A program package for the Landau
distribution", Computer Phys.Comm., 31(1984), 97-111
Double_t Na()
Avogadro constant (Avogadro's Number)
Double_t R()
universal gas constant (Na * K)
http://scienceworld.wolfram.com/physics/UniversalGasConstant.html
Double_t MWair()
Molecular weight of dry air
1976 US Standard Atmosphere,
also see http://atmos.nmsu.edu/jsdap/encyclopediawork.html
Double_t Rgair()
Dry Air Gas Constant (R / MWair)
http://atmos.nmsu.edu/education_and_outreach/encyclopedia/gas_constant.htm
Author: Francois-Xavier Gentit
Last update: root/base:$Name: $:$Id: TMath.cxx,v 1.115 2006/07/11 09:05:01 rdm Exp $
Copyright (C) 1995-2004, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.