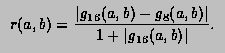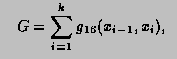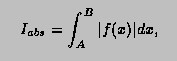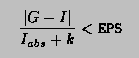library: libHist
#include "TF1.h" |
TF1
class description - header file - source file - inheritance tree (.pdf)
public:
TF1()
TF1(const char* name, const char* formula, Double_t xmin = 0, Double_t xmax = 1)
TF1(const char* name, Double_t xmin, Double_t xmax, Int_t npar)
TF1(const char* name, void* fcn, Double_t xmin, Double_t xmax, Int_t npar)
TF1(const TF1& f1)
virtual ~TF1()
static void AbsValue(Bool_t reject = kTRUE)
virtual void Browse(TBrowser* b)
static void CalcGaussLegendreSamplingPoints(Int_t num, Double_t* x, Double_t* w, Double_t eps = 3.0e-11)
virtual Double_t CentralMoment(Double_t n, Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001)
static TClass* Class()
virtual void Copy(TObject& f1) const
virtual Double_t Derivative(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const
virtual Double_t Derivative2(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const
virtual Double_t Derivative3(Double_t x, Double_t* params = 0, Double_t epsilon = 0.001) const
static Double_t DerivativeError()
virtual Int_t DistancetoPrimitive(Int_t px, Int_t py)
virtual void Draw(Option_t* option = "")
virtual TF1* DrawCopy(Option_t* option = "") const
virtual void DrawDerivative(Option_t* option = "al")
virtual void DrawF1(const char* formula, Double_t xmin, Double_t xmax, Option_t* option = "")
virtual void DrawIntegral(Option_t* option = "al")
virtual void DrawPanel()
virtual Double_t Eval(Double_t x, Double_t y = 0, Double_t z = 0, Double_t t = 0) const
virtual Double_t EvalPar(const Double_t* x, const Double_t* params = 0)
virtual void ExecuteEvent(Int_t event, Int_t px, Int_t py)
virtual void FixParameter(Int_t ipar, Double_t value)
Double_t GetChisquare() const
static TF1* GetCurrent()
TH1* GetHistogram() const
virtual Double_t GetMaximum(Double_t xmin = 0, Double_t xmax = 0) const
virtual Double_t GetMaximumX(Double_t xmin = 0, Double_t xmax = 0) const
TMethodCall* GetMethodCall() const
virtual Double_t GetMinimum(Double_t xmin = 0, Double_t xmax = 0) const
virtual Double_t GetMinimumX(Double_t xmin = 0, Double_t xmax = 0) const
virtual Int_t GetNDF() const
virtual Int_t GetNpx() const
virtual Int_t GetNumberFitPoints() const
virtual Int_t GetNumberFreeParameters() const
virtual char* GetObjectInfo(Int_t px, Int_t py) const
TObject* GetParent() const
virtual Double_t GetParError(Int_t ipar) const
virtual Double_t* GetParErrors() const
virtual void GetParLimits(Int_t ipar, Double_t& parmin, Double_t& parmax) const
virtual Double_t GetProb() const
virtual Int_t GetQuantiles(Int_t nprobSum, Double_t* q, const Double_t* probSum)
virtual Double_t GetRandom()
virtual Double_t GetRandom(Double_t xmin, Double_t xmax)
virtual void GetRange(Double_t& xmin, Double_t& xmax) const
virtual void GetRange(Double_t& xmin, Double_t& ymin, Double_t& xmax, Double_t& ymax) const
virtual void GetRange(Double_t& xmin, Double_t& ymin, Double_t& zmin, Double_t& xmax, Double_t& ymax, Double_t& zmax) const
virtual Double_t GetSave(const Double_t* x)
virtual Double_t GetX(Double_t y, Double_t xmin = 0, Double_t xmax = 0) const
TAxis* GetXaxis() const
virtual Double_t GetXmax() const
virtual Double_t GetXmin() const
TAxis* GetYaxis() const
TAxis* GetZaxis() const
virtual void GradientPar(const Double_t* x, Double_t* grad, Double_t eps = 0.01)
virtual void InitArgs(const Double_t* x, const Double_t* params)
static void InitStandardFunctions()
virtual Double_t Integral(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 1e-12)
virtual Double_t Integral(Double_t ax, Double_t bx, Double_t ay, Double_t by, Double_t epsilon = 1e-12)
virtual Double_t Integral(Double_t ax, Double_t bx, Double_t ay, Double_t by, Double_t az, Double_t bz, Double_t epsilon = 1e-12)
virtual Double_t IntegralFast(Int_t num, Double_t* x, Double_t* w, Double_t a, Double_t b, Double_t* params = 0)
virtual Double_t IntegralMultiple(Int_t n, const Double_t* a, const Double_t* b, Int_t minpts, Int_t maxpts, Double_t epsilon, Double_t& relerr, Int_t& nfnevl, Int_t& ifail)
virtual Double_t IntegralMultiple(Int_t n, const Double_t* a, const Double_t* b, Double_t epsilon, Double_t& relerr)
virtual TClass* IsA() const
virtual Bool_t IsInside(const Double_t* x) const
virtual Double_t Mean(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001)
Double_t MinimBrent(Int_t type, Double_t& xmin, Double_t& xmax, Double_t xmiddle, Double_t fy, Bool_t& ok) const
Double_t MinimStep(Int_t type, Double_t& xmin, Double_t& xmax, Double_t fy) const
virtual Double_t Moment(Double_t n, Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001)
TF1& operator=(const TF1& rhs)
virtual void Paint(Option_t* option = "")
virtual void Print(Option_t* option = "") const
static Bool_t RejectedPoint()
static void RejectPoint(Bool_t reject = kTRUE)
virtual void ReleaseParameter(Int_t ipar)
virtual void Save(Double_t xmin, Double_t xmax, Double_t ymin, Double_t ymax, Double_t zmin, Double_t zmax)
virtual void SavePrimitive(ostream& out, Option_t* option = "")
virtual void SetChisquare(Double_t chi2)
static void SetCurrent(TF1* f1)
virtual void SetFunction(Double_t (*)(Double_t*, Double_t*) fcn)
virtual void SetMaximum(Double_t maximum = -1111)
virtual void SetMinimum(Double_t minimum = -1111)
virtual void SetNDF(Int_t ndf)
virtual void SetNpx(Int_t npx = 100)
virtual void SetNumberFitPoints(Int_t npfits)
virtual void SetParent(TObject* p = 0)
virtual void SetParError(Int_t ipar, Double_t error)
virtual void SetParErrors(const Double_t* errors)
virtual void SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax)
virtual void SetRange(Double_t xmin, Double_t xmax)
virtual void SetRange(Double_t xmin, Double_t ymin, Double_t xmax, Double_t ymax)
virtual void SetRange(Double_t xmin, Double_t ymin, Double_t zmin, Double_t xmax, Double_t ymax, Double_t zmax)
virtual void SetSavedPoint(Int_t point, Double_t value)
virtual void SetTitle(const char* title = "")
virtual void ShowMembers(TMemberInspector& insp, char* parent)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
virtual void Update()
virtual Double_t Variance(Double_t a, Double_t b, const Double_t* params = 0, Double_t epsilon = 0.000001)
protected:
Double_t fXmin Lower bounds for the range
Double_t fXmax Upper bounds for the range
Int_t fNpx Number of points used for the graphical representation
Int_t fType (=0 for standard functions, 1 if pointer to function)
Int_t fNpfits Number of points used in the fit
Int_t fNDF Number of degrees of freedom in the fit
Int_t fNsave Number of points used to fill array fSave
Double_t fChisquare Function fit chisquare
Double_t* fIntegral ![fNpx] Integral of function binned on fNpx bins
Double_t* fParErrors [fNpar] Array of errors of the fNpar parameters
Double_t* fParMin [fNpar] Array of lower limits of the fNpar parameters
Double_t* fParMax [fNpar] Array of upper limits of the fNpar parameters
Double_t* fSave [fNsave] Array of fNsave function values
Double_t* fAlpha !Array alpha. for each bin in x the deconvolution r of fIntegral
Double_t* fBeta !Array beta. is approximated by x = alpha +beta*r *gamma*r**2
Double_t* fGamma !Array gamma.
TObject* fParent !Parent object hooking this function (if one)
TH1* fHistogram !Pointer to histogram used for visualisation
Double_t fMaximum Maximum value for plotting
Double_t fMinimum Minimum value for plotting
TMethodCall* fMethodCall !Pointer to MethodCall in case of interpreted function
Double_t (*)(Double_t*, Double_t*) fFunction !Pointer to function
static Bool_t fgAbsValue use absolute value of function when computing integral
static Bool_t fgRejectPoint True if point must be rejected in a fit
static TF1* fgCurrent pointer to current function being processed
public:
static const enum TF1:: kNotDraw
______________________________________________________________________________
a TF1 object is a 1-Dim function defined between a lower and upper limit.
The function may be a simple function (see TFormula) or a precompiled
user function.
The function may have associated parameters.
TF1 graphics function is via the TH1/TGraph drawing functions.
The following types of functions can be created:
A- Expression using variable x and no parameters
B- Expression using variable x with parameters
C- A general C function with parameters
+++++++++++++++++++++++++++++++++++
===> + Example of a function of type A +
+++++++++++++++++++++++++++++++++++
Case A1 (inline expression using standard C++ functions/operators)
------------------------------------------------------------------
TF1 *fa1 = new TF1("fa1","sin(x)/x",0,10);
fa1->Draw();
Case A2 (inline expression using TMath functions without parameters)
--------------------------------------------------------------------
TF1 *fa2 = new TF1("fa2","TMath::DiLog(x)",0,10);
fa2->Draw();
Case A3 (inline expression using a CINT function by name
--------------------------------------------------------
Double_t myFunc(x) {
return x+sin(x);
}
TF1 *fa3 = new TF1("fa4","myFunc(x)",-3,5);
fa3->Draw();
+++++++++++++++++++++++++++++++++++
===> + Example of a function of type B+
+++++++++++++++++++++++++++++++++++
Case B1 (inline expression using standard C++ functions/operators)
------------------------------------------------------------------
Example B1a
-----------
TF1 *fa = new TF1("fa","[0]*x*sin([1]*x)",-3,3);
This creates a function of variable x with 2 parameters.
The parameters must be initialized via:
fa->SetParameter(0,value_first_parameter);
fa->SetParameter(1,value_second_parameter);
Parameters may be given a name:
fa->SetParName(0,"Constant");
Example B1b
-----------
TF1 *fb = new TF1("fb","gaus(0)*expo(3)",0,10);
gaus(0) is a substitute for [0]*exp(-0.5*((x-[1])/[2])**2)
and (0) means start numbering parameters at 0
expo(3) is a substitute for exp([3]+[4]*x)
Case B2 (inline expression using TMath functions with parameters)
--------------------------------------------------------------------
TF1 *fb2 = new TF1("fa3","TMath::Landau(x,[0],[1],0)",-5,10);
fb2->SetParameters(0.2,1.3);
fb2->Draw();
+++++++++++++++++++++++++++++++++++
===> + Example of a function of type C+
+++++++++++++++++++++++++++++++++++
Consider the macro myfunc.C below
-------------macro myfunc.C-----------------------------
Double_t myfunction(Double_t *x, Double_t *par)
{
Float_t xx =x[0];
Double_t f = TMath::Abs(par[0]*sin(par[1]*xx)/xx);
return f;
}
void myfunc()
{
TF1 *f1 = new TF1("myfunc",myfunction,0,10,2);
f1->SetParameters(2,1);
f1->SetParNames("constant","coefficient");
f1->Draw();
}
void myfit()
{
TH1F *h1=new TH1F("h1","test",100,0,10);
h1->FillRandom("myfunc",20000);
TF1 *f1=gROOT->GetFunction("myfunc");
f1->SetParameters(800,1);
h1.Fit("myfunc");
}
--------end of macro myfunc.C---------------------------------
In an interactive session you can do:
Root > .L myfunc.C
Root > myfunc();
Root > myfit();
TF1 objects can reference other TF1 objects (thanks John Odonnell)
of type A or B defined above.This excludes CINT interpreted functions
and compiled functions.
However, there is a restriction. A function cannot reference a basic
function if the basic function is a polynomial polN.
Example:
{
TF1 *fcos = new TF1 ("fcos", "[0]*cos(x)", 0., 10.);
fcos->SetParNames( "cos");
fcos->SetParameter( 0, 1.1);
TF1 *fsin = new TF1 ("fsin", "[0]*sin(x)", 0., 10.);
fsin->SetParNames( "sin");
fsin->SetParameter( 0, 2.1);
TF1 *fsincos = new TF1 ("fsc", "fcos+fsin");
TF1 *fs2 = new TF1 ("fs2", "fsc+fsc");
}
WHY TF1 CANNOT ACCEPT A CLASS MEMBER FUNCTION ?
===============================================
This is a frequently asked question.
C++ is a strongly typed language. There is no way for TF1 (without
recompiling this class) to know about all possible user defined data types.
This also apply to the case of a static class function.
------------------------------------------------------------------------
TF1()
*-*-*-*-*-*-*-*-*-*-*F1 default constructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-* ======================
TF1(const char *name,const char *formula, Double_t xmin, Double_t xmax)
F1 constructor using a formula definition
See TFormula constructor for explanation of the formula syntax.
See tutorials: fillrandom, first, fit1, formula1, multifit
for real examples.
Creates a function of type A or B between xmin and xmax
if formula has the form "fffffff;xxxx;yyyy", it is assumed that
the formula string is "fffffff" and "xxxx" and "yyyy" are the
titles for the X and Y axis respectively.
TF1(const char *name, Double_t xmin, Double_t xmax, Int_t npar)
*-*-*-*-*-*-*F1 constructor using name of an interpreted function*-*-*-*
*-* =======================================================
*-*
*-* Creates a function of type C between xmin and xmax.
*-* name is the name of an interpreted CINT cunction.
*-* The function is defined with npar parameters
*-* fcn must be a function of type:
*-* Double_t fcn(Double_t *x, Double_t *params)
*-*
*-* This constructor is called for functions of type C by CINT.
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1(const char *name,void *fcn, Double_t xmin, Double_t xmax, Int_t npar)
*-*-*-*-*-*-*F1 constructor using pointer to an interpreted function*-*-*-*
*-* =======================================================
*-*
*-* See TFormula constructor for explanation of the formula syntax.
*-*
*-* Creates a function of type C between xmin and xmax.
*-* The function is defined with npar parameters
*-* fcn must be a function of type:
*-* Double_t fcn(Double_t *x, Double_t *params)
*-*
*-* see tutorial; myfit for an example of use
*-* also test/stress.cxx (see function stress1)
*-*
*-*
*-* This constructor is called for functions of type C by CINT.
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1(const char *name,Double_t (*fcn)(Double_t *, Double_t *), Double_t xmin, Double_t xmax, Int_t npar)
*-*-*-*-*-*-*F1 constructor using a pointer to real function*-*-*-*-*-*-*-*
*-* ===============================================
*-*
*-* npar is the number of free parameters used by the function
*-*
*-* This constructor creates a function of type C when invoked
*-* with the normal C++ compiler.
*-*
*-* see test program test/stress.cxx (function stress1) for an example.
*-* note the interface with an intermediate pointer.
*-*
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
~TF1()
*-*-*-*-*-*-*-*-*-*-*F1 default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-* =====================
void Copy(TObject &obj)
*-*-*-*-*-*-*-*-*-*-*Copy this F1 to a new F1*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-* ========================
Double_t Derivative(Double_t x, Double_t *params, Double_t eps)
returns the first derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
D(h) = (f(x+h) - f(x-h))/2h
the final estimate D = (4*D(h/2) - D(h))/3
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
if the argument params is null, the current function parameters are used,
otherwise the parameters in params are used.
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError
-----------------
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
err = k*Sqrt(f(x)*f(x) + x*x*deriv*deriv)*Sqrt(Sum(ai)*(ai)),
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Author: Anna Kreshuk
Double_t Derivative2(Double_t x, Double_t *params, Double_t eps)
returns the second derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
D(h) = (f(x+h) - 2*f(x) + f(x-h))/(h*h)
the final estimate D = (4*D(h/2) - D(h))/3
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
if the argument params is null, the current function parameters are used,
otherwise the parameters in params are used.
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError
-----------------
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
err = k*Sqrt(f(x)*f(x) + x*x*deriv*deriv)*Sqrt(Sum(ai)*(ai)),
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Author: Anna Kreshuk
Double_t Derivative3(Double_t x, Double_t *params, Double_t eps)
returns the third derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
D(h) = (f(x+2h) - 2*f(x+h) + 2*f(x-h) - f(x-2h))/(2*h*h*h)
the final estimate D = (4*D(h/2) - D(h))/3
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
if the argument params is null, the current function parameters are used,
otherwise the parameters in params are used.
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError
-----------------
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
err = k*Sqrt(f(x)*f(x) + x*x*deriv*deriv)*Sqrt(Sum(ai)*(ai)),
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Author: Anna Kreshuk
Int_t DistancetoPrimitive(Int_t px, Int_t py)
*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a function*-*-*-*-*
*-* ===============================================
*-* Compute the closest distance of approach from point px,py to this function.
*-* The distance is computed in pixels units.
*-*
*-* Note that px is called with a negative value when the TF1 is in
*-* TGraph or TH1 list of functions. In this case there is no point
*-* looking at the histogram axis.
*-*
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void Draw(Option_t *option)
*-*-*-*-*-*-*-*-*-*-*Draw this function with its current attributes*-*-*-*-*
*-* ==============================================
*-*
*-* Possible option values are:
*-* "SAME" superimpose on top of existing picture
*-* "L" connect all computed points with a straight line
*-* "C" connect all computed points with a smooth curve.
*-* "FC" draw a fill area below a smooth curve
*-*
*-* Note that the default value is "L". Therefore to draw on top
*-* of an existing picture, specify option "LSAME"
*-*
*-* NB. You must use DrawCopy if you want to draw several times the same
*-* function in the current canvas.
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1 * DrawCopy(Option_t *option)
*-*-*-*-*-*-*-*Draw a copy of this function with its current attributes*-*-*
*-* ========================================================
*-*
*-* This function MUST be used instead of Draw when you want to draw
*-* the same function with different parameters settings in the same canvas.
*-*
*-* Possible option values are:
*-* "SAME" superimpose on top of existing picture
*-* "L" connect all computed points with a straight line
*-* "C" connect all computed points with a smooth curve.
*-* "FC" draw a fill area below a smooth curve
*-*
*-* Note that the default value is "L". Therefore to draw on top
*-* of an existing picture, specify option "LSAME"
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void DrawDerivative(Option_t *option)
Draw derivative of this function
An intermediate TGraph object is built and drawn with option.
The resulting graph will be drawn into the current pad.
If this function is used via the context menu, it recommended
to create a new canvas/pad before invoking this function.
void DrawIntegral(Option_t *option)
Draw integral of this function
An intermediate TGraph object is built and drawn with option.
The resulting graph will be drawn into the current pad.
If this function is used via the context menu, it recommended
to create a new canvas/pad before invoking this function.
void DrawF1(const char *formula, Double_t xmin, Double_t xmax, Option_t *option)
*-*-*-*-*-*-*-*-*-*Draw formula between xmin and xmax*-*-*-*-*-*-*-*-*-*-*-*
*-* ==================================
*-*
void DrawPanel()
*-*-*-*-*-*-*Display a panel with all function drawing options*-*-*-*-*-*
*-* =================================================
*-*
*-* See class TDrawPanelHist for example
Double_t Eval(Double_t x, Double_t y, Double_t z, Double_t t)
*-*-*-*-*-*-*-*-*-*-*Evaluate this formula*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-* =====================
*-*
*-* Computes the value of this function (general case for a 3-d function)
*-* at point x,y,z.
*-* For a 1-d function give y=0 and z=0
*-* The current value of variables x,y,z is passed through x, y and z.
*-* The parameters used will be the ones in the array params if params is given
*-* otherwise parameters will be taken from the stored data members fParams
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t EvalPar(const Double_t *x, const Double_t *params)
*-*-*-*-*-*Evaluate function with given coordinates and parameters*-*-*-*-*-*
*-* =======================================================
*-*
Compute the value of this function at point defined by array x
and current values of parameters in array params.
If argument params is omitted or equal 0, the internal values
of parameters (array fParams) will be used instead.
For a 1-D function only x[0] must be given.
In case of a multi-dimemsional function, the arrays x must be
filled with the corresponding number of dimensions.
WARNING. In case of an interpreted function (fType=2), it is the
user's responsability to initialize the parameters via InitArgs
before calling this function.
InitArgs should be called at least once to specify the addresses
of the arguments x and params.
InitArgs should be called everytime these addresses change.
void ExecuteEvent(Int_t event, Int_t px, Int_t py)
*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
*-* =========================================
*-* This member function is called when a F1 is clicked with the locator
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
void FixParameter(Int_t ipar, Double_t value)
Fix the value of a parameter
The specified value will be used in a fit operation
TF1 * GetCurrent()
static function returning the current function being processed
TH1 * GetHistogram()
return a pointer to the histogram used to vusualize the function
Double_t GetMaximum(Double_t xmin, Double_t xmax)
return the maximum value of the function
Method:
First, the grid search is used to bracket the maximum
with the step size = (xmax-xmin)/fNpx. This way, the step size
can be controlled via the SetNpx() function. If the function is
unimodal or if its extrema are far apart, setting the fNpx to
a small value speeds the algorithm up many times.
Then, Brent's method is applied on the bracketed interval
Double_t GetMaximumX(Double_t xmin, Double_t xmax)
return the X value corresponding to the maximum value of the function
Method:
First, the grid search is used to bracket the maximum
with the step size = (xmax-xmin)/fNpx. This way, the step size
can be controlled via the SetNpx() function. If the function is
unimodal or if its extrema are far apart, setting the fNpx to
a small value speeds the algorithm up many times.
Then, Brent's method is applied on the bracketed interval
Double_t GetMinimum(Double_t xmin, Double_t xmax)
Returns the minimum value of the function on the (xmin, xmax) interval
Method:
First, the grid search is used to bracket the maximum
with the step size = (xmax-xmin)/fNpx. This way, the step size
can be controlled via the SetNpx() function. If the function is
unimodal or if its extrema are far apart, setting the fNpx to
a small value speeds the algorithm up many times.
Then, Brent's method is applied on the bracketed interval
Double_t GetMinimumX(Double_t xmin, Double_t xmax)
Returns the X value corresponding to the minimum value of the function on the
(xmin, xmax) interval
Method:
First, the grid search is used to bracket the maximum
with the step size = (xmax-xmin)/fNpx. This way, the step size
can be controlled via the SetNpx() function. If the function is
unimodal or if its extrema are far apart, setting the fNpx to
a small value speeds the algorithm up many times.
Then, Brent's method is applied on the bracketed interval
Double_t GetX(Double_t fy, Double_t xmin, Double_t xmax)
Returns the X value corresponding to the function value fy for (xmin<x<xmax).
Method:
First, the grid search is used to bracket the maximum
with the step size = (xmax-xmin)/fNpx. This way, the step size
can be controlled via the SetNpx() function. If the function is
unimodal or if its extrema are far apart, setting the fNpx to
a small value speeds the algorithm up many times.
Then, Brent's method is applied on the bracketed interval
Double_t MinimStep(Int_t type, Double_t &xmin, Double_t &xmax, Double_t fy)
Grid search implementation, used to bracket the minimum and later
use Brent's method with the bracketed interval
The step of the search is set to (xmax-xmin)/fNpx
type: 0-returns MinimumX
1-returns Minimum
2-returns MaximumX
3-returns Maximum
4-returns X corresponding to fy
Double_t MinimBrent(Int_t type, Double_t &xmin, Double_t &xmax, Double_t xmiddle, Double_t fy, Bool_t &ok)
Finds a minimum of a function, if the function is unimodal between xmin and xmax
This method uses a combination of golden section search and parabolic interpolation
Details about convergence and properties of this algorithm can be
found in the book by R.P.Brent "Algorithms for Minimization Without Derivatives"
or in the "Numerical Recipes", chapter 10.2
type: 0-returns MinimumX
1-returns Minimum
2-returns MaximumX
3-returns Maximum
4-returns X corresponding to fy
if ok=true the method has converged
Int_t GetNDF()
return the number of degrees of freedom in the fit
the fNDF parameter has been previously computed during a fit.
The number of degrees of freedom corresponds to the number of points
used in the fit minus the number of free parameters.
Int_t GetQuantiles(Int_t nprobSum, Double_t *q, const Double_t *probSum)
Compute Quantiles for density distribution of this function
Quantile x_q of a probability distribution Function F is defined as
F(x_q) = Integral_{xmin}^(x_q) f dx = q with 0 <= q <= 1.
For instance the median x_0.5 of a distribution is defined as that value
of the random variable for which the distribution function equals 0.5:
F(x_0.5) = Probability(x < x_0.5) = 0.5
code from Eddy Offermann, Renaissance
input parameters
- this TF1 function
- nprobSum maximum size of array q and size of array probSum
- probSum array of positions where quantiles will be computed.
It is assumed to contain at least nprobSum values.
output
- return value nq (<=nprobSum) with the number of quantiles computed
- array q filled with nq quantiles
Getting quantiles from two histograms and storing results in a TGraph,
a so-called QQ-plot
TGraph *gr = new TGraph(nprob);
f1->GetQuantiles(nprob,gr->GetX());
f2->GetQuantiles(nprob,gr->GetY());
gr->Draw("alp");
Double_t GetRandom()
Return a random number following this function shape
*-*
*-* The distribution contained in the function fname (TF1) is integrated
*-* over the channel contents.
*-* It is normalized to 1.
*-* For each bin the integral is approximated by a parabola.
*-* The parabola coefficients are stored as non persistent data members
*-* Getting one random number implies:
*-* - Generating a random number between 0 and 1 (say r1)
*-* - Look in which bin in the normalized integral r1 corresponds to
*-* - Evaluate the parabolic curve in the selected bin to find
*-* the corresponding X value.
*-* The parabolic approximation is very good as soon as the number
*-* of bins is greater than 50.
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
Double_t GetRandom(Double_t xmin, Double_t xmax)
Return a random number following this function shape in [xmin,xmax]
*-*
*-* The distribution contained in the function fname (TF1) is integrated
*-* over the channel contents.
*-* It is normalized to 1.
*-* For each bin the integral is approximated by a parabola.
*-* The parabola coefficients are stored as non persistent data members
*-* Getting one random number implies:
*-* - Generating a random number between 0 and 1 (say r1)
*-* - Look in which bin in the normalized integral r1 corresponds to
*-* - Evaluate the parabolic curve in the selected bin to find
*-* the corresponding X value.
*-* The parabolic approximation is very good as soon as the number
*-* of bins is greater than 50.
*-*
*-* IMPORTANT NOTE
*-* The integral of the function is computed at fNpx points. If the function
*-* has sharp peaks, you should increase the number of points (SetNpx)
*-* such that the peak is correctly tabulated at several points.
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
void GetRange(Double_t &xmin, Double_t &xmax)
*-*-*-*-*-*-*-*-*-*-*Return range of a 1-D function*-*-*-*-*-*-*-*-*-*-*-*
*-* ==============================
void GradientPar(const Double_t *x, Double_t *grad, Double_t eps)
Compute the gradient wrt parameters
Parameters:
x - point, were the gradient is computed
grad - used to return the computed gradient, assumed to be of at least fNpar size
eps - if the errors of parameters have been computed, the step used in
numerical differentiation is eps*parameter_error.
if the errors have not been computed, step=eps is used
default value of eps = 0.01
Method is the same as in Derivative() function
void InitArgs(const Double_t *x, const Double_t *params)
*-*-*-*-*-*-*-*-*-*-*Initialize parameters addresses*-*-*-*-*-*-*-*-*-*-*-*
*-* ===============================
Double_t Integral(Double_t a, Double_t b, const Double_t *params, Double_t epsilon)
*-*-*-*-*-*-*-*-*Return Integral of function between a and b*-*-*-*-*-*-*-*
based on original CERNLIB routine DGAUSS by Sigfried Kolbig
converted to C++ by Rene Brun
This function computes,
to an attempted specified accuracy, the value of the integral
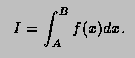
Usage:
In any arithmetic expression, this function
has the approximate value of the integral I.
- a,b
- End-points of integration interval. Note that B
may be less than A.
- params
- Array of function parameters. If 0, use current parameters.
- epsilon
- Accuracy parameter (see Accuracy).
Method:
For any interval [a,b] we define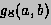 
and 
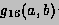to be the
8-point and 16-point Gaussian quadrature approximations to
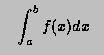
and define
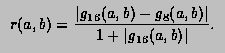
Then,
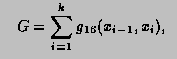
where, starting with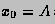 
and finishing with 
,
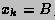the subdivision points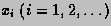 
are given by
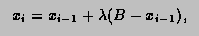
with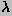 
equal to the first member of the sequence
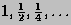for which
.
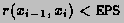If, at any stage in the process of subdivision, the ratio
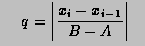
is so small that 1+0.005q is indistinguishable from 1 to
machine accuracy, an error exit occurs with the function value
set equal to zero.
Accuracy:
Unless there is severe cancellation of positive and negative
values of f(x) over the interval [A,B], the argument EPS
may be considered as specifying a bound on the relative error of
I in the case |I|>1, and a bound on the absolute error in
the case |I|<1. More precisely, if k is the number of sub-intervals
contributing to the approximation (see Method), and if
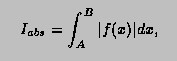
then the relation
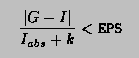
will nearly always be true, provided the routine terminates
without printing an error message. For functions
f having no singularities in the closed interval [A,B]
the accuracy will usually be much higher than this.
Error handling:
The requested accuracy cannot be
obtained (see Method).
The function value is set equal to zero.
Note1:
Values of the function f(x) at the interval end-points
A and B are not required. The subprogram may therefore
be used when these values are undefined.
Note2:
Instead of TF1::Integral, you may want to use the combination of
TF1::CalcGaussLegendreSamplingPoints and TF1::IntegralFast.
See an example with the following script:
void gint() {
TF1 *g = new TF1("g","gaus",-5,5);
g->SetParameters(1,0,1);
default gaus integration method uses 6 points
not suitable to integrate on a large domain
double r1 = g->Integral(0,5);
double r2 = g->Integral(0,1000);
try with user directives computing more points
Int_t np = 1000;
double *x=new double[np];
double *w=new double[np];
g->CalcGaussLegendreSamplingPoints(np,x,w,1e-15);
double r3 = g->IntegralFast(np,x,w,0,5);
double r4 = g->IntegralFast(np,x,w,0,1000);
double r5 = g->IntegralFast(np,x,w,0,10000);
double r6 = g->IntegralFast(np,x,w,0,100000);
printf("g->Integral(0,5) = %g\n",r1);
printf("g->Integral(0,1000) = %g\n",r2);
printf("g->IntegralFast(n,x,w,0,5) = %g\n",r3);
printf("g->IntegralFast(n,x,w,0,1000) = %g\n",r4);
printf("g->IntegralFast(n,x,w,0,10000) = %g\n",r5);
printf("g->IntegralFast(n,x,w,0,100000)= %g\n",r6);
delete [] x;
delete [] w;
}
This example produces the following results:
g->Integral(0,5) = 1.25331
g->Integral(0,1000) = 1.25319
g->IntegralFast(n,x,w,0,5) = 1.25331
g->IntegralFast(n,x,w,0,1000) = 1.25331
g->IntegralFast(n,x,w,0,10000) = 1.25331
g->IntegralFast(n,x,w,0,100000)= 1.253
---------------------------------------------------------------
Double_t Integral(Double_t, Double_t, Double_t, Double_t, Double_t, Double_t, Double_t)
Return Integral of a 3d function in range [ax,bx],[ay,by],[az,bz]
Double_t IntegralMultiple(Int_t n, const Double_t *a, const Double_t *b, Int_t minpts, Int_t maxpts, Double_t eps, Double_t &relerr,Int_t &nfnevl, Int_t &ifail)
Adaptive Quadrature for Multiple Integrals over N-Dimensional
Rectangular Regions
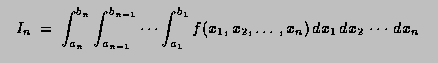
Author(s): A.C. Genz, A.A. Malik
converted/adapted by R.Brun to C++ from Fortran CERNLIB routine RADMUL (D120)
The new code features many changes compared to the Fortran version.
Note that this function is currently called only by TF2::Integral (n=2)
and TF3::Integral (n=3).
This function computes, to an attempted specified accuracy, the value of
the integral over an n-dimensional rectangular region.
input parameters
================
n : Number of dimensions [2,15]
a,b : One-dimensional arrays of length >= N . On entry A[i], and B[i],
contain the lower and upper limits of integration, respectively.
minpts: Minimum number of function evaluations requested. Must not exceed maxpts.
if minpts < 1 minpts is set to 2^n +2*n*(n+1) +1
maxpts: Maximum number of function evaluations to be allowed.
maxpts >= 2^n +2*n*(n+1) +1
if maxpts<minpts, maxpts is set to 10*minpts
eps : Specified relative accuracy.
output parameter
================
relerr : Contains, on exit, an estimation of the relative accuracy of the result.
nfnevl : number of function evaluations performed.
ifail :
0 Normal exit. . At least minpts and at most maxpts calls to the function were performed.
1 maxpts is too small for the specified accuracy eps.
The result and relerr contain the values obtainable for the
specified value of maxpts.
3 n<2 or n>15
Method:
=======
An integration rule of degree seven is used together with a certain
strategy of subdivision.
For a more detailed description of the method see References.
Notes:
1.Multi-dimensional integration is time-consuming. For each rectangular
subregion, the routine requires function evaluations.
Careful programming of the integrand might result in substantial saving
of time.
2.Numerical integration usually works best for smooth functions.
Some analysis or suitable transformations of the integral prior to
numerical work may contribute to numerical efficiency.
References:
1.A.C. Genz and A.A. Malik, Remarks on algorithm 006:
An adaptive algorithm for numerical integration over
an N-dimensional rectangular region, J. Comput. Appl. Math. 6 (1980) 295-302.
2.A. van Doren and L. de Ridder, An adaptive algorithm for numerical
integration over an n-dimensional cube, J.Comput. Appl. Math. 2 (1976) 207-217.
=========================================================================
void Paint(Option_t *option)
*-*-*-*-*-*-*-*-*-*-*Paint this function with its current attributes*-*-*-*-*
*-* ===============================================
void Print(Option_t *option)
*-*-*-*-*-*-*-*-*-*-*Dump this function with its attributes*-*-*-*-*-*-*-*-*-*
*-* ==================================
void ReleaseParameter(Int_t ipar)
Release parameter number ipar If used in a fit, the parameter
can vary freely. The parameter limits are reset to 0,0.
void SetCurrent(TF1 *f1)
static function setting the current function.
the current function may be accessed in static C-like functions
when fitting or painting a function.
void SetMaximum(Double_t maximum)
Set the maximum value along Y for this function
In case the function is already drawn, set also the maximum in the
helper histogram
void SetMinimum(Double_t minimum)
Set the minimum value along Y for this function
In case the function is already drawn, set also the minimum in the
helper histogram
void SetNDF(Int_t ndf)
Set the number of degrees of freedom
ndf should be the number of points used in a fit - the number of free parameters
void SetNpx(Int_t npx)
Set the number of points used to draw the function
The default number of points along x is 100 for 1-d functions and 30 for 2-d/3-d functions
You can increase this value to get a better resolution when drawing
pictures with sharp peaks or to get a better result when using TF1::GetRandom
the minimum number of points is 4, the maximum is 100000 for 1-d and 10000 for 2-d/3-d functions
void SetParErrors(const Double_t *errors)
set errors for all active parameters
when calling this function, the array errors must have at least fNpar values
void SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax)
*-*-*-*-*-*Set limits for parameter ipar*-*-*-*
*-* =============================
The specified limits will be used in a fit operation
when the option "B" is specified (Bounds).
To fix a parameter, use TF1::FixParameter
void SetRange(Double_t xmin, Double_t xmax)
*-*-*-*-*-*Initialize the upper and lower bounds to draw the function*-*-*-*
*-* ==========================================================
The function range is also used in an histogram fit operation
when the option "R" is specified.
void SetTitle(const char *title)
Set function title
if title has the form "fffffff;xxxx;yyyy", it is assumed that
the function title is "fffffff" and "xxxx" and "yyyy" are the
titles for the X and Y axis respectively.
void Streamer(TBuffer &b)
*-*-*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-* =========================================
void RejectPoint(Bool_t reject)
static function to set the global flag to reject points
the fgRejectPoint global flag is tested by all fit functions
if TRUE the point is not included in the fit.
This flag can be set by a user in a fitting function.
The fgRejectPoint flag is reset by the TH1 and TGraph fitting functions.
Author: Rene Brun 18/08/95
Last update: root/hist:$Name: $:$Id: TF1.cxx,v 1.128 2006/07/03 16:10:45 brun Exp $
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.