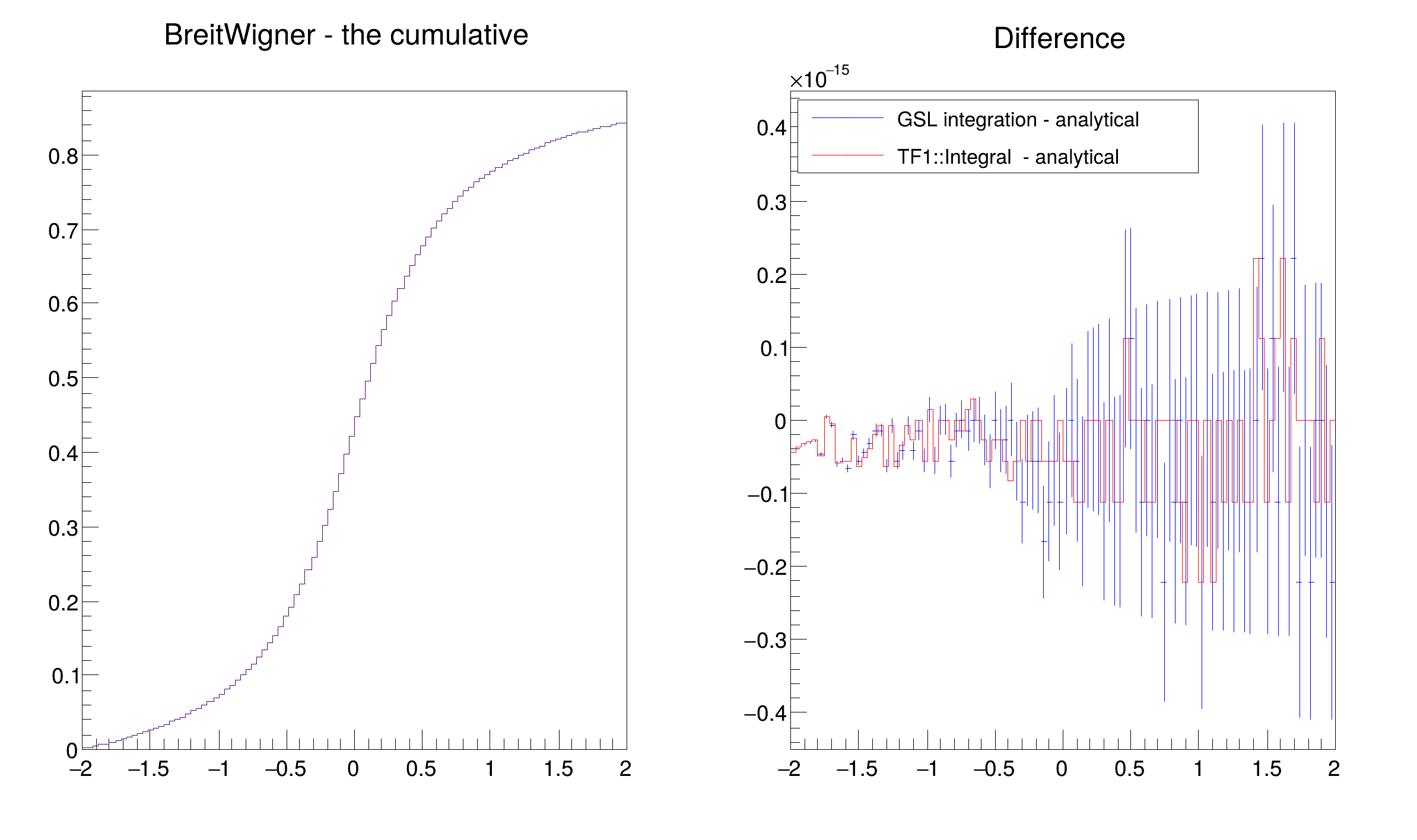
Example on the usage of the adaptive 1D integration algorithm of MathMore.
It calculates the numerically cumulative integral of a distribution (like in this case the BreitWigner) to execute the macro type it (you need to compile with AClic)
This tutorial requires having libMathMore built with ROOT.
To build mathmore you need to have a version of GSL >= 1.8 installed in your system The ROOT configure will automatically find GSL if the script gsl-config (from GSL) is in your PATH,. otherwise you need to configure root with the options –gsl-incdir and –gsl-libdir.
***************************************************************
Drawing cumulatives of BreitWigner in interval [ -2 , 2 ]
***************************************************************
***************************************************************
Test integration performances in interval [ -2 , 2 ]
Time using ROOT::Math::Integrator : 0.04668
Number of function calls = 69
42201.6649413923442
Time using TF1::Integral : 0.155544
Number of function calls = 91
42201.6649413923442
#include <iostream>
#include <limits>
int nc = 0;
}
nc++;
}
double func2(
const double *
x,
const double * =
nullptr){
nc++;
}
std::cout << "\n\n***************************************************************\n";
std::cout <<
"Test integration performances in interval [ " <<
x1 <<
" , " <<
x2 <<
" ]\n\n";
nc = 0;
for (
int i = 0; i <
n; ++i) {
}
std::cout <<
"Time using ROOT::Math::Integrator :\t" <<
timer.RealTime() << std::endl;
std::cout <<
"Number of function calls = " << nc/
n << std::endl;
int pr = std::cout.precision(18); std::cout <<
s1 << std::endl; std::cout.precision(
pr);
nc = 0;
for (
int i = 0; i <
n; ++i) {
}
std::cout <<
"Time using TF1::Integral :\t\t\t" <<
timer.RealTime() << std::endl;
std::cout <<
"Number of function calls = " << nc/
n << std::endl;
pr = std::cout.precision(18); std::cout <<
s1 << std::endl; std::cout.precision(
pr);
}
std::cout << "\n\n***************************************************************\n";
std::cout <<
"Drawing cumulatives of BreitWigner in interval [ " <<
x1 <<
" , " <<
x2 <<
" ]\n\n";
for (
int i = 1; i <=
n; ++i) {
}
for (
int i = 1; i <=
n; ++i) {
}
for (
int i = 1; i <=
n; ++i) {
}
for (
int i = 1; i <=
n; ++i) {
double delta =
cum1->GetBinContent(i) -
cum0->GetBinContent(i);
cum10->SetBinContent(i, delta );
cum10->SetBinError(i, std::numeric_limits<double>::epsilon() *
cum1->GetBinContent(i) );
}
cum0->SetTitle(
"BreitWigner - the cumulative");
cum10->SetTitle(
"Difference");
l->AddEntry(
cum10,
"GSL integration - analytical ");
l->AddEntry(
cum20,
"TF1::Integral - analytical ");
std::cout << "\n***************************************************************\n";
}
{
}
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
Option_t Option_t TPoint TPoint const char x2
Option_t Option_t TPoint TPoint const char x1
Functor1D class for one-dimensional functions.
User Class for performing numerical integration of a function in one dimension.
Template class to wrap any C++ callable object which takes one argument i.e.
1-D histogram with a double per channel (see TH1 documentation)
This class displays a legend box (TPaveText) containing several legend entries.
virtual void Draw(Option_t *option="")
Default Draw method for all objects.
@ kADAPTIVE
to be used for general functions without singularities
Double_t ATan(Double_t)
Returns the principal value of the arc tangent of x, expressed in radians.
Double_t BreitWigner(Double_t x, Double_t mean=0, Double_t gamma=1)
Calculates a Breit Wigner function with mean and gamma.
- Authors
- M. Slawinska, L. Moneta
Definition in file mathmoreIntegration.C.