rf316_llratioplot.C File Reference

Detailed Description

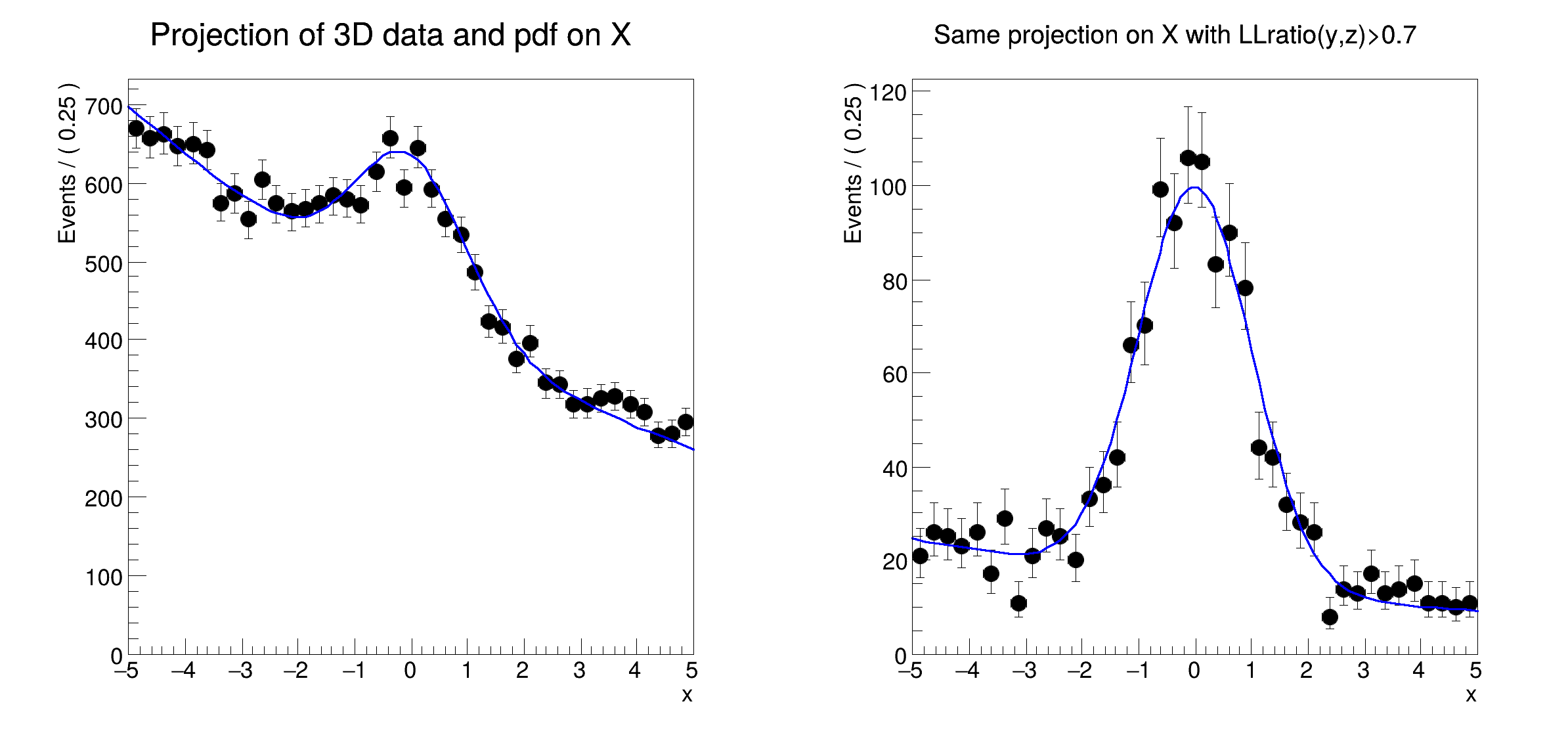
Multidimensional models: using the likelihood ratio technique to construct a signal enhanced one-dimensional projection of a multi-dimensional pdf

 
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooGaussian.h"
#include "RooPolynomial.h"
#include "RooAddPdf.h"
#include "RooProdPdf.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
using namespace RooFit;
 
void rf316_llratioplot()
{
 
   // C r e a t e   3 D   p d f   a n d   d a t a
   // -------------------------------------------
 
   // Create observables
   RooRealVar x("x", "x", -5, 5);
   RooRealVar y("y", "y", -5, 5);
   RooRealVar z("z", "z", -5, 5);
 
   // Create signal pdf gauss(x)*gauss(y)*gauss(z)
   RooGaussian gx("gx", "gx", x, 0.0, 1.0);
   RooGaussian gy("gy", "gy", y, 0.0, 1.0);
   RooGaussian gz("gz", "gz", z, 0.0, 1.0);
   RooProdPdf sig("sig", "sig", RooArgSet(gx, gy, gz));
 
   // Create background pdf poly(x)*poly(y)*poly(z)
   RooPolynomial px("px", "px", x, RooArgSet(-0.1, 0.004));
   RooPolynomial py("py", "py", y, RooArgSet(0.1, -0.004));
   RooPolynomial pz("pz", "pz", z);
   RooProdPdf bkg("bkg", "bkg", RooArgSet(px, py, pz));
 
   // Create composite pdf sig+bkg
   RooRealVar fsig("fsig", "signal fraction", 0.1, 0., 1.);
   RooAddPdf model("model", "model", RooArgList(sig, bkg), fsig);
 
   std::unique_ptr<RooDataSet> data{model.generate({x, y, z}, 20000)};
 
   // P r o j e c t   p d f   a n d   d a t a   o n   x
   // -------------------------------------------------
 
   // Make plain projection of data and pdf on x observable
   RooPlot *frame = x.frame(Title("Projection of 3D data and pdf on X"), Bins(40));
   data->plotOn(frame);
   model.plotOn(frame);
 
   // D e f i n e   p r o j e c t e d   s i g n a l   l i k e l i h o o d   r a t i o
   // ----------------------------------------------------------------------------------
 
   // Calculate projection of signal and total likelihood on (y,z) observables
   // i.e. integrate signal and composite model over x
   RooAbsPdf *sigyz = sig.createProjection(x);
   RooAbsPdf *totyz = model.createProjection(x);
 
   // Construct the log of the signal / signal+background probability
   RooFormulaVar llratio_func("llratio", "log10(@0)-log10(@1)", RooArgList(*sigyz, *totyz));
 
   // P l o t   d a t a   w i t h   a   L L r a t i o   c u t
   // -------------------------------------------------------
 
   // Calculate the llratio value for each event in the dataset
   data->addColumn(llratio_func);
 
   // Extract the subset of data with large signal likelihood
   std::unique_ptr<RooAbsData> dataSel{data->reduce(Cut("llratio>0.7"))};
 
   // Make plot frame
   RooPlot *frame2 = x.frame(Title("Same projection on X with LLratio(y,z)>0.7"), Bins(40));
 
   // Plot select data on frame
   dataSel->plotOn(frame2);
 
   // M a k e   M C   p r o j e c t i o n   o f   p d f   w i t h   s a m e   L L r a t i o   c u t
   // ---------------------------------------------------------------------------------------------
 
   // Generate large number of events for MC integration of pdf projection
   std::unique_ptr<RooDataSet> mcprojData{model.generate({x, y, z}, 10000)};
 
   // Calculate LL ratio for each generated event and select MC events with llratio)0.7
   mcprojData->addColumn(llratio_func);
   std::unique_ptr<RooAbsData> mcprojDataSel{mcprojData->reduce(Cut("llratio>0.7"))};
 
   // Project model on x, integrating projected observables (y,z) with Monte Carlo technique
   // on set of events with the same llratio cut as was applied to data
   model.plotOn(frame2, ProjWData(*mcprojDataSel));
 
   TCanvas *c = new TCanvas("rf316_llratioplot", "rf316_llratioplot", 800, 400);
   c->Divide(2);
   c->cd(1);
   gPad->SetLeftMargin(0.15);
   frame->GetYaxis()->SetTitleOffset(1.4);
   frame->Draw();
   c->cd(2);
   gPad->SetLeftMargin(0.15);
   frame2->GetYaxis()->SetTitleOffset(1.4);
   frame2->Draw();
}

 
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) plot on x integrates over variables (y,z)
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) plot on x averages using data variables (y,z)
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) only the following components of the projection data will be used: (y,z)
[#1] INFO:Fitting -- using CPU computation library compiled with -mavx2

Date

July 2008

Author

Wouter Verkerke

Definition in file rf316_llratioplot.C.