With default parameters the macro will attempt to run the standard hist2workspace example and read the ROOT file that it produces.
This uses a modified version of the profile likelihood ratio as a test statistic for upper limits (eg. test stat = 0 if muhat>mu).
Based on the observed data, one defines a set of parameter points to be tested based on the value of the parameter of interest and the conditional MLE (eg. profiled) values of the nuisance parameters.
At each parameter point, pseudo-experiments are generated using this fixed reference model and then the test statistic is evaluated. The auxiliary measurements (global observables) associated with the constraint terms in nuisance parameters are also fluctuated in the process of generating the pseudo-experiments in a frequentist manner forming an 'unconditional ensemble'. One could form a 'conditional' ensemble in which these auxiliary measurements are fixed. Note that the nuisance parameters are not randomized, which is a Bayesian procedure. Note, the nuisance parameters are floating in the fits. For each point, the threshold that defines the 95% acceptance region is found. This forms a "Confidence Belt".
After constructing the confidence belt, one can find the confidence interval for any particular dataset by finding the intersection of the observed test statistic and the confidence belt. First this is done on the observed data to get an observed 1-sided upper limt.
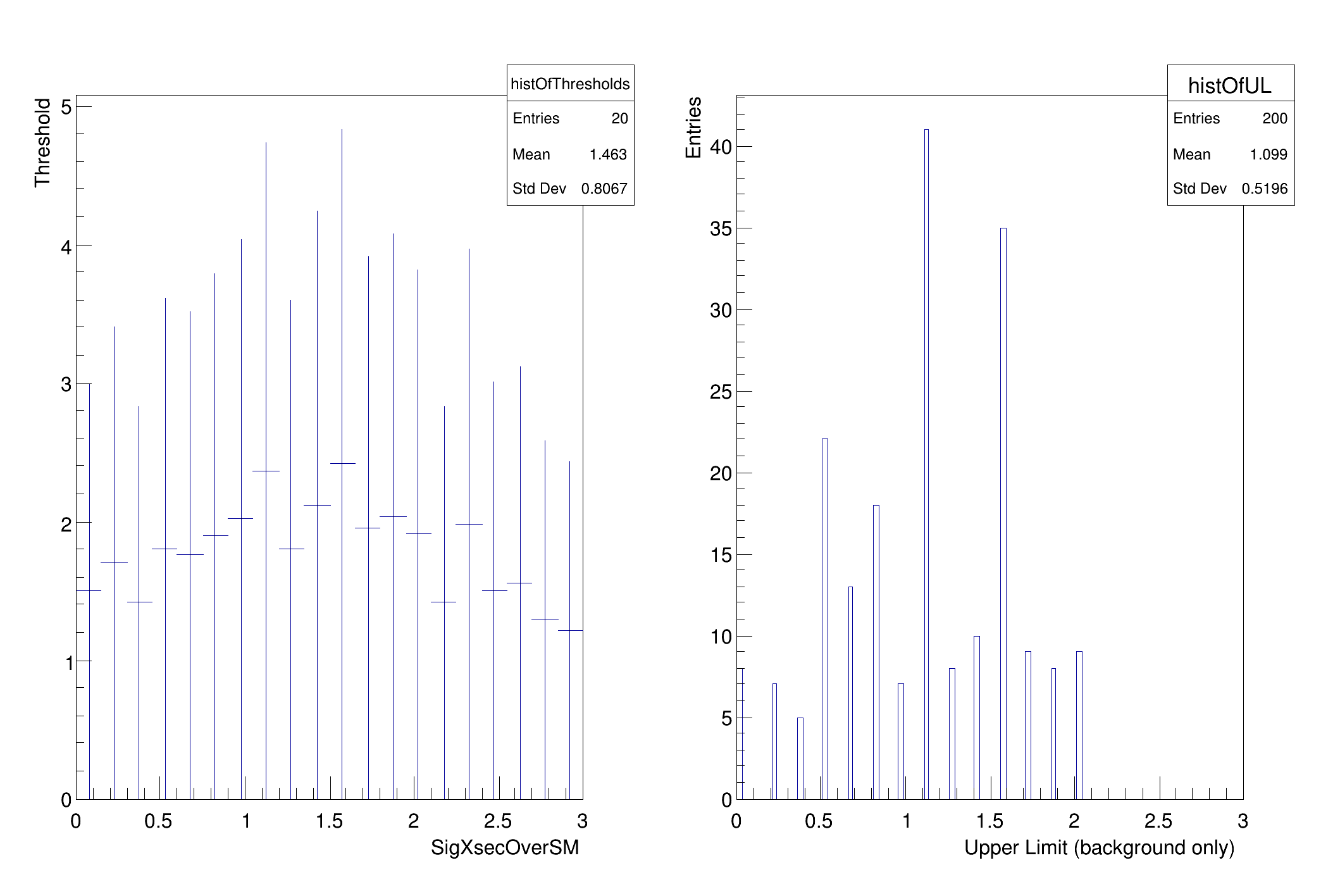
Finally, there expected limit and bands (from background-only) are formed by generating background-only data and finding the upper limit. The background-only is defined as such that the nuisance parameters are fixed to their best fit value based on the data with the signal rate fixed to 0. The bands are done by hand for now, will later be part of the RooStats tools.
On a technical note, this technique IS the generalization of Feldman-Cousins with nuisance parameters.
Building the confidence belt can be computationally expensive. Once it is built, one could save it to a file and use it in a separate step.
We can use PROOF to speed things along in parallel, however, the test statistic has to be installed on the workers so either turn off PROOF or include the modified test statistic in your $ROOTSYS/roofit/roostats/inc directory, add the additional line to the LinkDef.h file, and recompile root.
Note, if you have a boundary on the parameter of interest (eg. cross-section) the threshold on the two-sided test statistic starts off at moderate values and plateaus.
[#0] PROGRESS:Generation – generated toys: 500 / 999 NeymanConstruction: Prog: 12/50 total MC = 39 this test stat = 0 SigXsecOverSM=0.69 alpha_syst1=0.136515 alpha_syst3=0.425415 beta_syst2=1.08496 [-1e+30, 0.011215] in interval = 1
this tells you the values of the parameters being used to generate the pseudo-experiments and the threshold in this case is 0.011215. One would expect for 95% that the threshold would be ~1.35 once the cross-section is far enough away from 0 that it is essentially unaffected by the boundary. As one reaches the last points in the scan, the theshold starts to get artificially high. This is because the range of the parameter in the fit is the same as the range in the scan. In the future, these should be independently controlled, but they are not now. As a result the ~50% of pseudo-experiments that have an upward fluctuation end up with muhat = muMax. Because of this, the upper range of the parameter should be well above the expected upper limit... but not too high or one will need a very large value of nPointsToScan to resolve the relevant region. This can be improved, but this is the first version of this script.
Important note: when the model includes external constraint terms, like a Gaussian constraint to a nuisance parameter centered around some nominal value there is a subtlety. The asymptotic results are all based on the assumption that all the measurements fluctuate... including the nominal values from auxiliary measurements. If these do not fluctuate, this corresponds to an "conditional ensemble". The result is that the distribution of the test statistic can become very non-chi^2. This results in thresholds that become very large.
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
Found data and ModelConfig:
=== Using the following for ModelConfig ===
Observables: RooArgSet:: = (obs_x_channel1,weightVar,channelCat)
Parameters of Interest: RooArgSet:: = (SigXsecOverSM)
Nuisance Parameters: RooArgSet:: = (alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
Global Observables: RooArgSet:: = (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
PDF: RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.174888
FeldmanCousins: ntoys per point = 499
FeldmanCousins: nEvents per toy will fluctuate about expectation
will use global observables for unconditional ensemble
RooArgSet:: = (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
=== Using the following for ModelConfig ===
Observables: RooArgSet:: = (obs_x_channel1,weightVar,channelCat)
Parameters of Interest: RooArgSet:: = (SigXsecOverSM)
Nuisance Parameters: RooArgSet:: = (alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
Global Observables: RooArgSet:: = (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
PDF: RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.174888
FeldmanCousins: Model has nuisance parameters, will do profile construction
FeldmanCousins: # points to test = 20
lookup index = 0
NeymanConstruction: Prog: 1/20 total MC = 499 this test stat = 1.54009
SigXsecOverSM=0.075 alpha_syst2=0.656048 alpha_syst3=0.244567 gamma_stat_channel1_bin_0=1.03397 gamma_stat_channel1_bin_1=1.04971 [-1e+30, 1.4945] in interval = 0
NeymanConstruction: Prog: 2/20 total MC = 499 this test stat = 1.12274
SigXsecOverSM=0.225 alpha_syst2=0.549579 alpha_syst3=0.211046 gamma_stat_channel1_bin_0=1.02849 gamma_stat_channel1_bin_1=1.04283 [-1e+30, 1.70069] in interval = 1
NeymanConstruction: Prog: 3/20 total MC = 499 this test stat = 0.77243
SigXsecOverSM=0.375 alpha_syst2=0.44775 alpha_syst3=0.177828 gamma_stat_channel1_bin_0=1.02318 gamma_stat_channel1_bin_1=1.03602 [-1e+30, 1.41504] in interval = 1
NeymanConstruction: Prog: 4/20 total MC = 499 this test stat = 0.488545
SigXsecOverSM=0.525 alpha_syst2=0.349863 alpha_syst3=0.144895 gamma_stat_channel1_bin_0=1.01804 gamma_stat_channel1_bin_1=1.02929 [-1e+30, 1.80371] in interval = 1
NeymanConstruction: Prog: 5/20 total MC = 499 this test stat = 0.270334
SigXsecOverSM=0.675 alpha_syst2=0.255203 alpha_syst3=0.11224 gamma_stat_channel1_bin_0=1.01307 gamma_stat_channel1_bin_1=1.02264 [-1e+30, 1.75591] in interval = 1
NeymanConstruction: Prog: 6/20 total MC = 499 this test stat = 0.11689
SigXsecOverSM=0.825 alpha_syst2=0.16608 alpha_syst3=0.0821439 gamma_stat_channel1_bin_0=1.00838 gamma_stat_channel1_bin_1=1.01547 [-1e+30, 1.89781] in interval = 1
NeymanConstruction: Prog: 7/20 total MC = 499 this test stat = 0.0271562
SigXsecOverSM=0.975 alpha_syst2=0.0745784 alpha_syst3=0.0487673 gamma_stat_channel1_bin_0=1.00375 gamma_stat_channel1_bin_1=1.00931 [-1e+30, 2.02136] in interval = 1
NeymanConstruction: Prog: 8/20 total MC = 499 this test stat = 0.000125096
SigXsecOverSM=1.125 alpha_syst2=-0.0140996 alpha_syst3=0.0151511 gamma_stat_channel1_bin_0=0.999297 gamma_stat_channel1_bin_1=1.00317 [-1e+30, 2.36523] in interval = 1
NeymanConstruction: Prog: 9/20 total MC = 499 this test stat = 0.0347209
SigXsecOverSM=1.275 alpha_syst2=-0.101327 alpha_syst3=-0.0176472 gamma_stat_channel1_bin_0=0.994967 gamma_stat_channel1_bin_1=0.99714 [-1e+30, 1.79773] in interval = 1
NeymanConstruction: Prog: 10/20 total MC = 499 this test stat = 0.12986
SigXsecOverSM=1.425 alpha_syst2=-0.185801 alpha_syst3=-0.0506339 gamma_stat_channel1_bin_0=0.990814 gamma_stat_channel1_bin_1=0.991141 [-1e+30, 2.11797] in interval = 1
NeymanConstruction: Prog: 11/20 total MC = 499 this test stat = 0.284381
SigXsecOverSM=1.575 alpha_syst2=-0.266353 alpha_syst3=-0.0784096 gamma_stat_channel1_bin_0=0.987025 gamma_stat_channel1_bin_1=0.984445 [-1e+30, 2.41483] in interval = 1
NeymanConstruction: Prog: 12/20 total MC = 499 this test stat = 0.497424
SigXsecOverSM=1.725 alpha_syst2=-0.3458 alpha_syst3=-0.10947 gamma_stat_channel1_bin_0=0.983247 gamma_stat_channel1_bin_1=0.978371 [-1e+30, 1.95432] in interval = 1
NeymanConstruction: Prog: 13/20 total MC = 499 this test stat = 0.767852
SigXsecOverSM=1.875 alpha_syst2=-0.422672 alpha_syst3=-0.140541 gamma_stat_channel1_bin_0=0.979595 gamma_stat_channel1_bin_1=0.972417 [-1e+30, 2.03922] in interval = 1
NeymanConstruction: Prog: 14/20 total MC = 499 this test stat = 1.09468
SigXsecOverSM=2.025 alpha_syst2=-0.496602 alpha_syst3=-0.171004 gamma_stat_channel1_bin_0=0.976094 gamma_stat_channel1_bin_1=0.966484 [-1e+30, 1.90696] in interval = 1
NeymanConstruction: Prog: 15/20 total MC = 499 this test stat = 1.47704
SigXsecOverSM=2.175 alpha_syst2=-0.567566 alpha_syst3=-0.201186 gamma_stat_channel1_bin_0=0.972718 gamma_stat_channel1_bin_1=0.960626 [-1e+30, 1.41513] in interval = 0
NeymanConstruction: Prog: 16/20 total MC = 499 this test stat = 1.91389
SigXsecOverSM=2.325 alpha_syst2=-0.63553 alpha_syst3=-0.231072 gamma_stat_channel1_bin_0=0.96946 gamma_stat_channel1_bin_1=0.954845 [-1e+30, 1.98699] in interval = 1
NeymanConstruction: Prog: 17/20 total MC = 499 this test stat = 2.40432
SigXsecOverSM=2.475 alpha_syst2=-0.700748 alpha_syst3=-0.261131 gamma_stat_channel1_bin_0=0.966278 gamma_stat_channel1_bin_1=0.949239 [-1e+30, 1.50323] in interval = 0
NeymanConstruction: Prog: 18/20 total MC = 499 this test stat = 2.94737
SigXsecOverSM=2.625 alpha_syst2=-0.763083 alpha_syst3=-0.290538 gamma_stat_channel1_bin_0=0.963225 gamma_stat_channel1_bin_1=0.943654 [-1e+30, 1.5594] in interval = 0
NeymanConstruction: Prog: 19/20 total MC = 499 this test stat = 3.54205
SigXsecOverSM=2.775 alpha_syst2=-0.822865 alpha_syst3=-0.319576 gamma_stat_channel1_bin_0=0.960275 gamma_stat_channel1_bin_1=0.938148 [-1e+30, 1.29457] in interval = 0
NeymanConstruction: Prog: 20/20 total MC = 499 this test stat = 4.18752
SigXsecOverSM=2.925 alpha_syst2=-0.880381 alpha_syst3=-0.348221 gamma_stat_channel1_bin_0=0.957426 gamma_stat_channel1_bin_1=0.932721 [-1e+30, 1.21599] in interval = 0
[#1] INFO:Eval -- 14 points in interval
95% interval on SigXsecOverSM is : [0.225, 2.325]
[#1] INFO:Minization -- p.d.f. provides expected number of events, including extended term in likelihood.
[#1] INFO:Minization -- createNLL picked up cached consraints from workspace with 6 entries
[#1] INFO:Minization -- Including the following constraint terms in minimization: (lumiConstraint,alpha_syst1Constraint,alpha_syst2Constraint,alpha_syst3Constraint,gamma_stat_channel1_bin_0_constraint,gamma_stat_channel1_bin_1_constraint)
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_simPdf_obsData_with_constr_Profile[SigXsecOverSM]) Creating instance of MINUIT
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_simPdf_obsData_with_constr) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_simPdf_obsData_with_constr_Profile[SigXsecOverSM]) determining minimum likelihood for current configurations w.r.t all observable
RooAbsTestStatistic::initSimMode: creating slave calculator #0 for state channel1 (2 dataset entries)
[#1] INFO:Fitting -- RooAbsTestStatistic::initSimMode: created 1 slave calculators.
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_simPdf_obsData_with_constr_Profile[SigXsecOverSM]) minimum found at (SigXsecOverSM=1.11597)
.
Will use these parameter points to generate pseudo data for bkg only
1) 0x56028c8fd3c0 RooRealVar:: alpha_syst2 = 0.711172 +/- 0.914106 L(-5 - 5) "alpha_syst2"
2) 0x56028ca8f280 RooRealVar:: alpha_syst3 = 0.26146 +/- 0.9291 L(-5 - 5) "alpha_syst3"
3) 0x56028cc75b30 RooRealVar:: gamma_stat_channel1_bin_0 = 1.03677 +/- 0.0462899 L(0 - 1.25) "gamma_stat_channel1_bin_0"
4) 0x56028c9f3580 RooRealVar:: gamma_stat_channel1_bin_1 = 1.05319 +/- 0.0761205 L(0 - 1.5) "gamma_stat_channel1_bin_1"
5) 0x56028c9ee920 RooRealVar:: SigXsecOverSM = 0 +/- 0 L(0 - 3) B(20) "SigXsecOverSM"
-2 sigma band 0
-1 sigma band 0.495 [Power Constraint)]
median of band 1.095
+1 sigma band 1.545
+2 sigma band 1.995
observed 95% upper-limit 2.325
CLb strict [P(toy>obs|0)] for observed 95% upper-limit 0.96
CLb inclusive [P(toy>=obs|0)] for observed 95% upper-limit 0.96
#include <iostream>
using namespace std;
bool useProof = false;
int nworkers = 0;
void TwoSidedFrequentistUpperLimitWithBands(const char *infile = "", const char *workspaceName = "combined",
const char *modelConfigName = "ModelConfig",
const char *dataName = "obsData")
{
double confidenceLevel = 0.95;
double additionalToysFac = 0.5;
int nPointsToScan = 20;
int nToyMC = 200;
const char *filename = "";
if (!strcmp(infile, "")) {
filename = "results/example_combined_GaussExample_model.root";
if (!fileExist) {
#ifdef _WIN32
cout << "HistFactory file cannot be generated on Windows - exit" << endl;
return;
#endif
cout << "will run standard hist2workspace example" << endl;
gROOT->ProcessLine(
".! prepareHistFactory .");
gROOT->ProcessLine(
".! hist2workspace config/example.xml");
cout << "\n\n---------------------" << endl;
cout << "Done creating example input" << endl;
cout << "---------------------\n\n" << endl;
}
} else
filename = infile;
cout << "StandardRooStatsDemoMacro: Input file " << filename << " is not found" << endl;
return;
}
if (!w) {
cout << "workspace not found" << endl;
return;
}
ModelConfig *mc = (ModelConfig *)w->
obj(modelConfigName);
if (!data || !mc) {
cout << "data or ModelConfig was not found" << endl;
return;
}
cout << "Found data and ModelConfig:" << endl;
mc->Print();
FeldmanCousins
fc(*data, *mc);
fc.SetConfidenceLevel(confidenceLevel);
fc.AdditionalNToysFactor(additionalToysFac);
fc.SetNBins(nPointsToScan);
ToyMCSampler *toymcsampler = (ToyMCSampler *)
fc.GetTestStatSampler();
ProfileLikelihoodTestStat *testStat = dynamic_cast<ProfileLikelihoodTestStat *>(toymcsampler->GetTestStatistic());
if (!mc->GetPdf()->canBeExtended()) {
fc.FluctuateNumDataEntries(
false);
else
cout << "Not sure what to do about this model" << endl;
}
if (useProof) {
ProofConfig
pc(*w, nworkers,
"",
false);
toymcsampler->SetProofConfig(&
pc);
}
if (mc->GetGlobalObservables()) {
cout << "will use global observables for unconditional ensemble" << endl;
mc->GetGlobalObservables()->Print();
toymcsampler->SetGlobalObservables(*mc->GetGlobalObservables());
}
PointSetInterval *interval =
fc.GetInterval();
ConfidenceBelt *belt =
fc.GetConfidenceBelt();
cout <<
"\n95% interval on " << firstPOI->
GetName() <<
" is : [" << interval->LowerLimit(*firstPOI) <<
", " << interval->UpperLimit(*firstPOI) << "] " << endl;
double observedUL = interval->UpperLimit(*firstPOI);
double obsTSatObsUL =
fc.GetTestStatSampler()->EvaluateTestStatistic(*data, tmpPOI);
double arMax = belt->GetAcceptanceRegionMax(*tmpPoint);
histOfThresholds->
Fill(poiVal, arMax);
}
histOfThresholds->
Draw();
if (mc->GetNuisanceParameters())
poiAndNuisance->
add(*mc->GetNuisanceParameters());
poiAndNuisance->
add(*mc->GetParametersOfInterest());
cout << "\nWill use these parameter points to generate pseudo data for bkg only" << endl;
paramsToGenerateData->
Print(
"v");
unconditionalObs.
add(*mc->GetObservables());
unconditionalObs.
add(*mc->GetGlobalObservables());
double CLb = 0;
double CLbinclusive = 0;
TH1F *histOfUL =
new TH1F(
"histOfUL",
"", 100, 0, firstPOI->
getMax());
for (int imc = 0; imc < nToyMC; ++imc) {
if (!mc->GetPdf()->canBeExtended()) {
toyData = mc->GetPdf()->generate(*mc->GetObservables(), 1);
else
cout << "Not sure what to do about this model" << endl;
} else {
toyData = mc->GetPdf()->generate(*mc->GetObservables(),
Extended());
}
if (!simPdf) {
RooDataSet *one = mc->GetPdf()->generate(*mc->GetGlobalObservables(), 1);
RooArgSet *allVars = mc->GetPdf()->getVariables();
*allVars = *values;
delete allVars;
delete one;
} else {
RooArgSet *allVars = mc->GetPdf()->getVariables();
*allVars = *values;
delete allVars;
delete one;
}
double toyTSatObsUL =
fc.GetTestStatSampler()->EvaluateTestStatistic(*toyData, tmpPOI);
if (obsTSatObsUL < toyTSatObsUL)
CLb += (1.) / nToyMC;
if (obsTSatObsUL <= toyTSatObsUL)
CLbinclusive += (1.) / nToyMC;
double thisUL = 0;
double arMax = belt->GetAcceptanceRegionMax(*tmpPoint);
double thisTS =
fc.GetTestStatSampler()->EvaluateTestStatistic(*toyData, tmpPOI);
if (thisTS <= arMax) {
} else {
break;
}
}
delete toyData;
}
c1->SaveAs(
"two-sided_upper_limit_output.pdf");
double band2sigDown = 0, band1sigDown = 0, bandMedian = 0, band1sigUp = 0, band2sigUp = 0;
for (
int i = 1; i <= cumulative->
GetNbinsX(); ++i) {
if (bins[i] < 0.5)
}
cout << "-2 sigma band " << band2sigDown << endl;
cout << "-1 sigma band " << band1sigDown << " [Power Constraint)]" << endl;
cout << "median of band " << bandMedian << endl;
cout << "+1 sigma band " << band1sigUp << endl;
cout << "+2 sigma band " << band2sigUp << endl;
cout << "\nobserved 95% upper-limit " << interval->UpperLimit(*firstPOI) << endl;
cout << "CLb strict [P(toy>obs|0)] for observed 95% upper-limit " << CLb << endl;
cout << "CLb inclusive [P(toy>=obs|0)] for observed 95% upper-limit " << CLbinclusive << endl;
delete profile;
delete nll;
}
R__EXTERN TSystem * gSystem
static struct mg_connection * fc(struct mg_context *ctx)
Double_t getRealValue(const char *name, Double_t defVal=0, Bool_t verbose=kFALSE) const
Get value of a RooAbsReal stored in set with given name.
virtual void Print(Option_t *options=0) const
This method must be overridden when a class wants to print itself.
RooAbsData is the common abstract base class for binned and unbinned datasets.
virtual Int_t numEntries() const
virtual Double_t getMax(const char *name=0) const
Get maximum of currently defined range.
virtual Double_t getMin(const char *name=0) const
Get miniminum of currently defined range.
RooAbsReal is the common abstract base class for objects that represent a real value and implements f...
virtual RooAbsReal * createProfile(const RooArgSet ¶msOfInterest)
Create a RooProfileLL object that eliminates all nuisance parameters in the present function.
Double_t getVal(const RooArgSet *normalisationSet=nullptr) const
Evaluate object.
RooArgSet is a container object that can hold multiple RooAbsArg objects.
RooArgSet * snapshot(bool deepCopy=true) const
Use RooAbsCollection::snapshot(), but return as RooArgSet.
virtual TObject * clone(const char *newname) const
virtual Bool_t add(const RooAbsCollection &col, Bool_t silent=kFALSE)
Add a collection of arguments to this collection by calling add() for each element in the source coll...
RooDataSet is a container class to hold unbinned data.
virtual const RooArgSet * get(Int_t index) const override
Return RooArgSet with coordinates of event 'index'.
RooRealVar represents a variable that can be changed from the outside.
virtual void setVal(Double_t value)
Set value of variable to 'value'.
RooSimultaneous facilitates simultaneous fitting of multiple PDFs to subsets of a given dataset.
virtual RooDataSet * generateSimGlobal(const RooArgSet &whatVars, Int_t nEvents)
Special generator interface for generation of 'global observables' – for RooStats tools.
The RooWorkspace is a persistable container for RooFit projects.
RooAbsData * data(const char *name) const
Retrieve dataset (binned or unbinned) with given name. A null pointer is returned if not found.
void Print(Option_t *opts=0) const
Print contents of the workspace.
Bool_t saveSnapshot(const char *name, const char *paramNames)
Save snapshot of values and attributes (including "Constant") of given parameters.
Bool_t loadSnapshot(const char *name)
Load the values and attributes of the parameters in the snapshot saved with the given name.
TObject * obj(const char *name) const
Return any type of object (RooAbsArg, RooAbsData or generic object) with given name)
A ROOT file is a suite of consecutive data records (TKey instances) with a well defined format.
static TFile * Open(const char *name, Option_t *option="", const char *ftitle="", Int_t compress=ROOT::RCompressionSetting::EDefaults::kUseCompiledDefault, Int_t netopt=0)
Create / open a file.
1-D histogram with a float per channel (see TH1 documentation)}
virtual Double_t GetBinCenter(Int_t bin) const
Return bin center for 1D histogram.
TAxis * GetXaxis()
Get the behaviour adopted by the object about the statoverflows. See EStatOverflows for more informat...
TObject * Clone(const char *newname=0) const
Make a complete copy of the underlying object.
virtual Int_t GetNbinsX() const
virtual Int_t Fill(Double_t x)
Increment bin with abscissa X by 1.
virtual void SetContent(const Double_t *content)
Replace bin contents by the contents of array content.
virtual void SetMinimum(Double_t minimum=-1111)
virtual void Draw(Option_t *option="")
Draw this histogram with options.
virtual Double_t * GetIntegral()
Return a pointer to the array of bins integral.
virtual void SetTitle(const char *title="")
Set the title of the TNamed.
virtual const char * GetName() const
Returns name of object.
virtual Bool_t AccessPathName(const char *path, EAccessMode mode=kFileExists)
Returns FALSE if one can access a file using the specified access mode.
RooCmdArg Extended(Bool_t flag=kTRUE)
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...
Namespace for the RooStats classes.
Double_t SignificanceToPValue(Double_t Z)
returns p-value corresponding to a 1-sided significance
static constexpr double pc

 TwoSidedFrequentistUpperLimitWithBands
TwoSidedFrequentistUpperLimitWithBands