______________________________________________________________________________
The H I S T O G R A M Classes
===============================
ROOT supports the following histogram types:
1-D histograms:
TH1C : histograms with one byte per channel. Maximum bin content = 255
TH1S : histograms with one short per channel. Maximum bin content = 65535
TH1I : histograms with one int per channel. Maximum bin content = 2147483647
TH1F : histograms with one float per channel. Maximum precision 7 digits
TH1D : histograms with one double per channel. Maximum precision 14 digits
2-D histograms:
TH2C : histograms with one byte per channel. Maximum bin content = 255
TH2S : histograms with one short per channel. Maximum bin content = 65535
TH2I : histograms with one int per channel. Maximum bin content = 2147483647
TH2F : histograms with one float per channel. Maximum precision 7 digits
TH2D : histograms with one double per channel. Maximum precision 14 digits
3-D histograms:
TH3C : histograms with one byte per channel. Maximum bin content = 255
TH3S : histograms with one short per channel. Maximum bin content = 65535
TH3I : histograms with one int per channel. Maximum bin content = 2147483647
TH3F : histograms with one float per channel. Maximum precision 7 digits
TH3D : histograms with one double per channel. Maximum precision 14 digits
Profile histograms: See classes TProfile and TProfile2D
Profile histograms are used to display the mean value of Y and its RMS
for each bin in X. Profile histograms are in many cases an elegant
replacement of two-dimensional histograms : the inter-relation of two
measured quantities X and Y can always be visualized by a two-dimensional
histogram or scatter-plot; If Y is an unknown (but single-valued)
approximate function of X, this function is displayed by a profile
histogram with much better precision than by a scatter-plot.
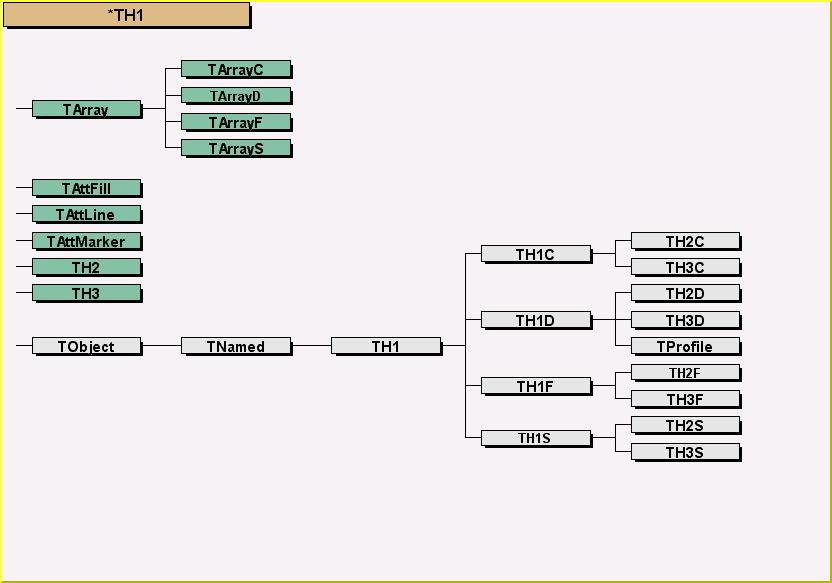
- All histogram classes are derived from the base class TH1
TH1
^
|
|
|
-----------------------------------------------------------
| | | | | | |
| | TH1C TH1S TH1I TH1F TH1D
| | |
| | |
| TH2 TProfile
| |
| |
| ----------------------------------
| | | | | |
| TH2C TH2S TH2I TH2F TH2D
| |
TH3 |
| TProfile2D
|
-------------------------------------
| | | | |
TH3C TH3S TH3I TH3F TH3D
The TH*C classes also inherit from the array class TArrayC.
The TH*S classes also inherit from the array class TArrayS.
The TH*I classes also inherit from the array class TArrayI.
The TH*F classes also inherit from the array class TArrayF.
The TH*D classes also inherit from the array class TArrayD.
Creating histograms
===================
Histograms are created by invoking one of the constructors, eg
TH1F *h1 = new TH1F("h1","h1 title",100,0,4.4);
TH2F *h2 = new TH2F("h2","h2 title",40,0,4,30,-3,3);
histograms may also be created by:
- calling the Clone function, see below
- making a projection from a 2-D or 3-D histogram, see below
- reading an histogram from a file
When an histogram is created, a reference to it is automatically added
to the list of in-memory objects for the current file or directory.
This default behaviour can be changed by:
h->SetDirectory(0); // for the current histogram h
TH1::AddDirectory(kFALSE); // sets a global switch disabling the reference
When the histogram is deleted, the reference to it is removed from
the list of objects in memory.
When a file is closed, all histograms in memory associated with this file
are automatically deleted.
Fix or variable bin size
========================
All histogram types support either fix or variable bin sizes.
2-D histograms may have fix size bins along X and variable size bins
along Y or vice-versa. The functions to fill, manipulate, draw or access
histograms are identical in both cases.
Each histogram always contains 3 objects TAxis: fXaxis, fYaxis and fZaxis
To access the axis parameters, do:
TAxis *xaxis = h->GetXaxis(); etc.
Double_t binCenter = xaxis->GetBinCenter(bin), etc.
See class TAxis for a description of all the access functions.
The axis range is always stored internally in double precision.
Convention for numbering bins
=============================
For all histogram types: nbins, xlow, xup
bin = 0; underflow bin
bin = 1; first bin with low-edge xlow INCLUDED
bin = nbins; last bin with upper-edge xup EXCLUDED
bin = nbins+1; overflow bin
In case of 2-D or 3-D histograms, a "global bin" number is defined.
For example, assuming a 3-D histogram with binx,biny,binz, the function
Int_t gbin = h->GetBin(binx,biny,binz);
returns a global/linearized gbin number. This global gbin is useful
to access the bin content/error information independently of the dimension.
Note that to access the information other than bin content and errors
one should use the TAxis object directly with eg:
Double_t xcenter = h3->GetZaxis()->GetBinCenter(27);
returns the center along z of bin number 27 (not the global bin)
in the 3-d histogram h3.
Alphanumeric Bin Labels
=======================
By default, an histogram axis is drawn with its numeric bin labels.
One can specify alphanumeric labels instead with:
1- call TAxis::SetBinLabel(bin,label);
This can always be done before or after filling.
When the histogram is drawn, bin labels will be automatically drawn.
See example in $ROOTSYS/tutorials/labels1.C, labels2.C
2- call to a Fill function with one of the arguments being a string, eg
hist1->Fill(somename,weigth);
hist2->Fill(x,somename,weight);
hist2->Fill(somename,y,weight);
hist2->Fill(somenamex,somenamey,weight);
See example in $ROOTSYS/tutorials/hlabels1.C, hlabels2.C
3- via TTree::Draw.
see for example $ROOTSYS/tutorials/cern.C
tree.Draw("Nation::Division"); where "Nation" and "Division"
are two branches of a Tree.
When using the options 2 or 3 above, the labels are automatically
added to the list (THashList) of labels for a given axis.
By default, an axis is drawn with the order of bins corresponding
to the filling sequence. It is possible to reorder the axis
- alphabetically
- by increasing or decreasing values
The reordering can be triggered via the TAxis contextMenu by selecting
the menu item "LabelsOption" or by calling directly
TH1::LabelsOption(option,axis) where
-axis may be "X","Y" or "Z"
-option may be:
option = "a" sort by alphabetic order
= ">" sort by decreasing values
= "<" sort by increasing values
= "h" draw labels horizonthal
= "v" draw labels vertical
= "u" draw labels up (end of label right adjusted)
= "d" draw labels down (start of label left adjusted)
When using the option 2 above, new labels are added by doubling the current
number of bins in case one label does not exist yet.
When the Filling is terminated, it is possible to trim the number
of bins to match the number of active labels by calling
TH1::LabelsDeflate(axis) with axis = "X","Y" or "Z"
This operation is automatic when using TTree::Draw.
Once bin labels have been created, they become persistent if the histogram
is written to a file or when generating the C++ code via SavePrimitive.
Histograms with automatic bins
==============================
When an histogram is created with an axis lower limit greater or equal
to its upper limit, the SetBuffer is automatically called with an
argument fBufferSize equal to fgBufferSize (default value=1000).
fgBufferSize may be reset via the static function TH1::SetDefaultBufferSize.
The axis limits will be automatically computed when the buffer will
be full or when the function BufferEmpty is called.
Filling histograms
==================
An histogram is typically filled with statements like:
h1->Fill(x);
h1->Fill(x,w); //fill with weight
h2->Fill(x,y)
h2->Fill(x,y,w)
h3->Fill(x,y,z)
h3->Fill(x,y,z,w)
or via one of the Fill functions accepting names described above.
The Fill functions compute the bin number corresponding to the given
x,y or z argument and increment this bin by the given weight.
The Fill functions return the bin number for 1-D histograms or global
bin number for 2-D and 3-D histograms.
If TH1::Sumw2 has been called before filling, the sum of squares of
weights is also stored.
One can also increment directly a bin number via TH1::AddBinContent
or replace the existing content via TH1::SetBinContent.
To access the bin content of a given bin, do:
Double_t binContent = h->GetBinContent(bin);
By default, the bin number is computed using the current axis ranges.
If the automatic binning option has been set via
h->SetBit(TH1::kCanRebin);
then, the Fill Function will automatically extend the axis range to
accomodate the new value specified in the Fill argument. The method
used is to double the bin size until the new value fits in the range,
merging bins two by two. This automatic binning options is extensively
used by the TTree::Draw function when histogramming Tree variables
with an unknown range.
This automatic binning option is supported for 1-d, 2-D and 3-D histograms.
During filling, some statistics parameters are incremented to compute
the mean value and Root Mean Square with the maximum precision.
In case of histograms of type TH1C, TH1S, TH2C, TH2S, TH3C, TH3S
a check is made that the bin contents do not exceed the maximum positive
capacity (127 or 65535). Histograms of all types may have positive
or/and negative bin contents.
Rebinning
=========
At any time, an histogram can be rebinned via TH1::Rebin. This function
returns a new histogram with the rebinned contents.
If bin errors were stored, they are recomputed during the rebinning.
Associated errors
=================
By default, for each bin, the sum of weights is computed at fill time.
One can also call TH1::Sumw2 to force the storage and computation
of the sum of the square of weights per bin.
If Sumw2 has been called, the error per bin is computed as the
sqrt(sum of squares of weights), otherwise the error is set equal
to the sqrt(bin content).
To return the error for a given bin number, do:
Double_t error = h->GetBinError(bin);
Associated functions
====================
One or more object (typically a TF1*) can be added to the list
of functions (fFunctions) associated to each histogram.
When TH1::Fit is invoked, the fitted function is added to this list.
Given an histogram h, one can retrieve an associated function
with: TF1 *myfunc = h->GetFunction("myfunc");
Operations on histograms
========================
Many types of operations are supported on histograms or between histograms
- Addition of an histogram to the current histogram
- Additions of two histograms with coefficients and storage into the current
histogram
- Multiplications and Divisions are supported in the same way as additions.
- The Add, Divide and Multiply functions also exist to add,divide or multiply
an histogram by a function.
If an histogram has associated error bars (TH1::Sumw2 has been called),
the resulting error bars are also computed assuming independent histograms.
In case of divisions, Binomial errors are also supported.
Fitting histograms
==================
Histograms (1-D,2-D,3-D and Profiles) can be fitted with a user
specified function via TH1::Fit. When an histogram is fitted, the
resulting function with its parameters is added to the list of functions
of this histogram. If the histogram is made persistent, the list of
associated functions is also persistent. Given a pointer (see above)
to an associated function myfunc, one can retrieve the function/fit
parameters with calls such as:
Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
Double_t err0 = myfunc->GetParError(0); //error on first parameter
Projections of histograms
========================
One can:
- make a 1-D projection of a 2-D histogram or Profile
see functions TH2::ProjectionX,Y, TH2::ProfileX,Y, TProfile::ProjectionX
- make a 1-D, 2-D or profile out of a 3-D histogram
see functions TH3::ProjectionZ, TH3::Project3D.
One can fit these projections via:
TH2::FitSlicesX,Y, TH3::FitSlicesZ.
Random Numbers and histograms
=============================
TH1::FillRandom can be used to randomly fill an histogram using
the contents of an existing TF1 function or another
TH1 histogram (for all dimensions).
For example the following two statements create and fill an histogram
10000 times with a default gaussian distribution of mean 0 and sigma 1:
TH1F h1("h1","histo from a gaussian",100,-3,3);
h1.FillRandom("gaus",10000);
TH1::GetRandom can be used to return a random number distributed
according the contents of an histogram.
Making a copy of an histogram
=============================
Like for any other ROOT object derived from TObject, one can use
the Clone() function. This makes an identical copy of the original
histogram including all associated errors and functions, e.g.:
TH1F *hnew = (TH1F*)h->Clone("hnew");
Normalizing histograms
======================
One can scale an histogram such that the bins integral is equal to
the normalization parameter via TH1::Scale(Double_t norm).
Drawing histograms
==================
Histograms are drawn via the THistPainter class. Each histogram has
a pointer to its own painter (to be usable in a multithreaded program).
Many drawing options are supported.
See THistPainter::Paint() for more details.
The same histogram can be drawn with different options in different pads.
When an histogram drawn in a pad is deleted, the histogram is
automatically removed from the pad or pads where it was drawn.
If an histogram is drawn in a pad, then filled again, the new status
of the histogram will be automatically shown in the pad next time
the pad is updated. One does not need to redraw the histogram.
To draw the current version of an histogram in a pad, one can use
h->DrawCopy();
This makes a clone (see Clone below) of the histogram. Once the clone
is drawn, the original histogram may be modified or deleted without
affecting the aspect of the clone.
One can use TH1::SetMaximum() and TH1::SetMinimum() to force a particular
value for the maximum or the minimum scale on the plot.
TH1::UseCurrentStyle() can be used to change all histogram graphics
attributes to correspond to the current selected style.
This function must be called for each histogram.
In case one reads and draws many histograms from a file, one can force
the histograms to inherit automatically the current graphics style
by calling before gROOT->ForceStyle().
Setting Drawing histogram contour levels (2-D hists only)
=========================================================
By default contours are automatically generated at equidistant
intervals. A default value of 20 levels is used. This can be modified
via TH1::SetContour() or TH1::SetContourLevel().
the contours level info is used by the drawing options "cont", "surf",
and "lego".
Setting histogram graphics attributes
=====================================
The histogram classes inherit from the attribute classes:
TAttLine, TAttFill, TAttMarker and TAttText.
See the member functions of these classes for the list of options.
Giving titles to the X, Y and Z axis
====================================
h->GetXaxis()->SetTitle("X axis title");
h->GetYaxis()->SetTitle("Y axis title");
The histogram title and the axis titles can be any TLatex string.
The titles are part of the persistent histogram.
It is also possible to specify the histogram title and the axis
titles at creation time. These titles can be given in the "title"
parameter. They must be separated by ";":
TH1F* h=new TH1F("h","Histogram title;X Axis;Y Axis;Z Axis",100,0,1);
Any title can be omitted:
TH1F* h=new TH1F("h","Histogram title;;Y Axis",100,0,1);
TH1F* h=new TH1F("h",";;Y Axis",100,0,1);
The method SetTitle has the same syntax:
h->SetTitle("Histogram title;An other X title Axis");
Saving/Reading histograms to/from a ROOT file
=============================================
The following statements create a ROOT file and store an histogram
on the file. Because TH1 derives from TNamed, the key identifier on
the file is the histogram name:
TFile f("histos.root","new");
TH1F h1("hgaus","histo from a gaussian",100,-3,3);
h1.FillRandom("gaus",10000);
h1->Write();
To Read this histogram in another Root session, do:
TFile f("histos.root");
TH1F *h = (TH1F*)f.Get("hgaus");
One can save all histograms in memory to the file by:
file->Write();
Miscelaneous operations
=======================
TH1::KolmogorovTest(): statistical test of compatibility in shape
between two histograms
TH1::Smooth() smooths the bin contents of a 1-d histogram
TH1::Integral() returns the integral of bin contents in a given bin range
TH1::GetMean(int axis) returns the mean value along axis
TH1::GetRMS(int axis) returns the sigma distribution along axis
TH1::GetEntries() returns the number of entries
TH1::Reset() resets the bin contents and errors of an histogram