rf611_weightedfits.C File Reference

Detailed Description

Likelihood and minimization: Parameter uncertainties for weighted unbinned ML fits

Parameter uncertainties for weighted unbinned ML fits

Based on example from https://arxiv.org/abs/1911.01303

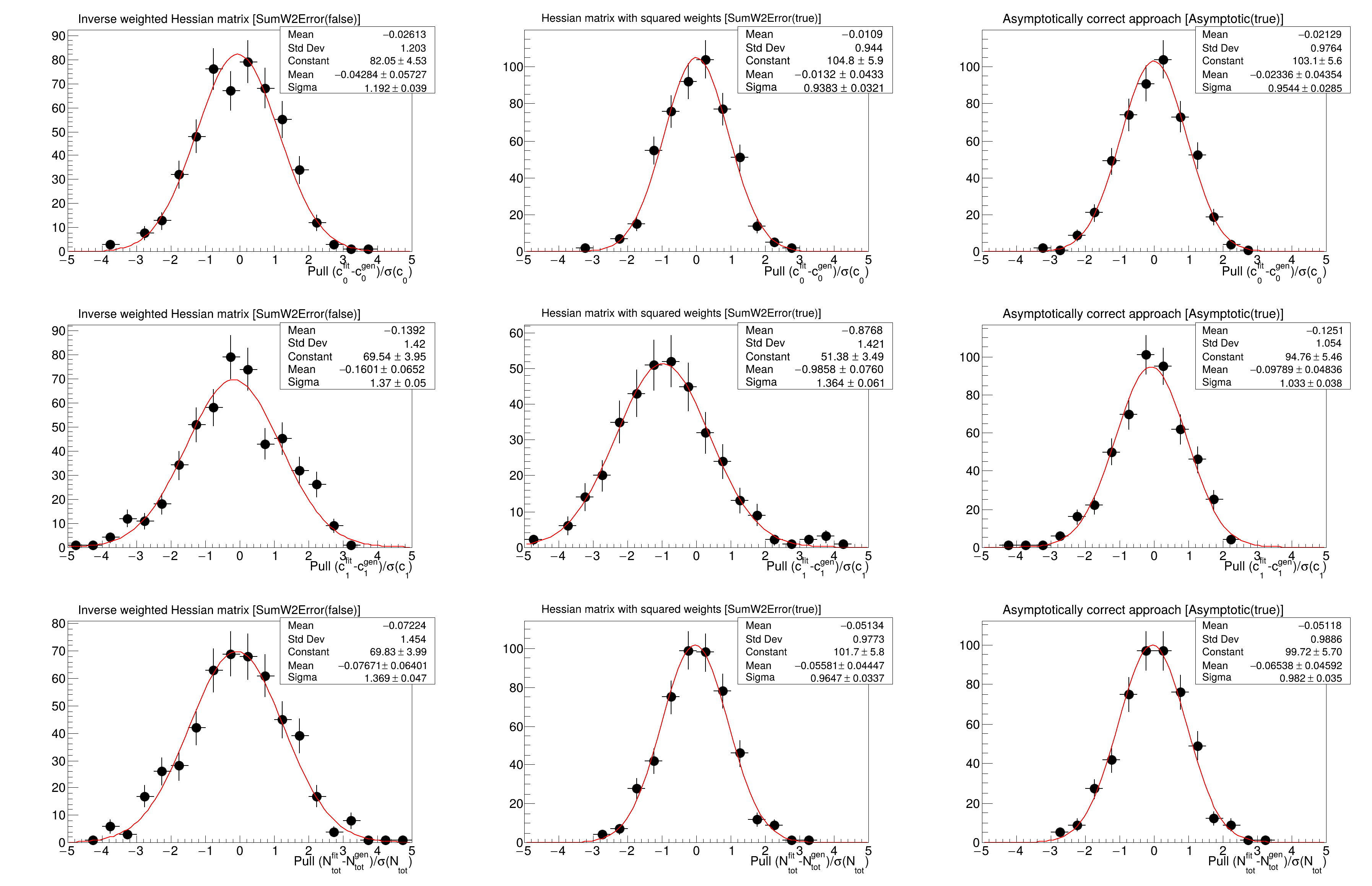
This example compares different approaches to determining parameter uncertainties in weighted unbinned maximum likelihood fits. Performing a weighted unbinned maximum likelihood fits can be useful to account for acceptance effects and to statistically subtract background events using the sPlot formalism. It is however well known that the inverse Hessian matrix does not yield parameter uncertainties with correct coverage in the presence of event weights. Three approaches to the determination of parameter uncertainties are compared in this example:

1. Using the inverse weighted Hessian matrix [SumW2Error(false)]
2. Using the expression [SumW2Error(true)]

   \[ V_{ij} = H_{ik}^{-1} C_{kl} H_{lj}^{-1} \]

   where H is the weighted Hessian matrix and C is the Hessian matrix with squared weights
3. The asymptotically correct approach (for details please see https://arxiv.org/abs/1911.01303) [Asymptotic(true)]

   \[ V_{ij} = H_{ik}^{-1} D_{kl} H_{lj}^{-1} \]

   where H is the weighted Hessian matrix and D is given by

   \[ D_{kl} = \sum_{e=1}^{N} w_e^2 \frac{\partial \log(P)}{\partial \lambda_k}\frac{\partial \log(P)}{\partial \lambda_l} \]

   with the event weight \(w_e\).

The example performs the fit of a second order polynomial in the angle cos(theta) [-1,1] to a weighted data set. The polynomial is given by

\[ P = \frac{ 1 + c_0 \cdot \cos(\theta) + c_1 \cdot \cos(\theta) \cdot \cos(\theta) }{\mathrm{Norm}} \]

The two coefficients \( c_0 \) and \( c_1 \) and their uncertainties are to be determined in the fit.

The per-event weight is used to correct for an acceptance effect, two different acceptance models can be studied:

• acceptancemodel==1: eff = \( 0.3 + 0.7 \cdot \cos(\theta) \cdot \cos(\theta) \)
• acceptancemodel==2: eff = \( 1.0 - 0.7 \cdot \cos(\theta) \cdot \cos(\theta) \) The data is generated to be flat before the acceptance effect.

The performance of the different approaches to determine parameter uncertainties is compared using the pull distributions from a large number of pseudoexperiments. The pull is defined as \( (\lambda_i - \lambda_{gen})/\sigma(\lambda_i) \), where \( \lambda_i \) is the fitted parameter and \( \sigma(\lambda_i) \) its uncertainty for pseudoexperiment number i. If the fit is unbiased and the parameter uncertainties are estimated correctly, the pull distribution should be a Gaussian centered around zero with a width of one.

 
#include "TH1D.h"
#include "TCanvas.h"
#include "TROOT.h"
#include "TStyle.h"
#include "TRandom3.h"
#include "TLegend.h"
#include "RooRealVar.h"
#include "RooFitResult.h"
#include "RooDataSet.h"
#include "RooPolynomial.h"
 
using namespace RooFit;
 
void rf611_weightedfits(int acceptancemodel = 2)
{
   // I n i t i a l i s a t i o n   a n d   S e t u p
   //------------------------------------------------
 
   // plotting options
   gStyle->SetPaintTextFormat(".1f");
   gStyle->SetEndErrorSize(6.0);
   gStyle->SetTitleSize(0.05, "XY");
   gStyle->SetLabelSize(0.05, "XY");
   gStyle->SetTitleOffset(0.9, "XY");
   gStyle->SetTextSize(0.05);
   gStyle->SetPadLeftMargin(0.125);
   gStyle->SetPadBottomMargin(0.125);
   gStyle->SetPadTopMargin(0.075);
   gStyle->SetPadRightMargin(0.075);
   gStyle->SetMarkerStyle(20);
   gStyle->SetMarkerSize(1.0);
   gStyle->SetHistLineWidth(2.0);
   gStyle->SetHistLineColor(1);
 
   // initialise TRandom3
   TRandom3 *rnd = new TRandom3();
   rnd->SetSeed(191101303);
 
   // accepted events and events weighted to account for the acceptance
   TH1 *haccepted = new TH1D("haccepted", "Generated events;cos(#theta);#events", 40, -1.0, 1.0);
   TH1 *hweighted = new TH1D("hweighted", "Generated events;cos(#theta);#events", 40, -1.0, 1.0);
   // histograms holding pull distributions
   std::array<TH1 *, 3> hc0pull;
   std::array<TH1 *, 3> hc1pull;
   std::array<TH1 *, 3> hntotpull;
   std::array<std::string, 3> methodLabels{"Inverse weighted Hessian matrix [SumW2Error(false)]",
                                           "Hessian matrix with squared weights [SumW2Error(true)]",
                                           "Asymptotically correct approach [Asymptotic(true)]"};
   auto makePullXLabel = [](std::string const &pLabel) {
      return "Pull (" + pLabel + "^{fit}-" + pLabel + "^{gen})/#sigma(" + pLabel + ")";
   };
   for (std::size_t i = 0; i < 3; ++i) {
      std::string const &iLabel = std::to_string(i);
      // using the inverse Hessian matrix
      std::string hc0XLabel = methodLabels[i] + ";" + makePullXLabel("c_{0}") + ";";
      std::string hc1XLabel = methodLabels[i] + ";" + makePullXLabel("c_{1}") + ";";
      std::string hntotXLabel = methodLabels[i] + ";" + makePullXLabel("N_{tot}") + ";";
      hc0pull[i] = new TH1D(("hc0pull" + iLabel).c_str(), hc0XLabel.c_str(), 20, -5.0, 5.0);
      // using the correction with the Hessian matrix with squared weights
      hc1pull[i] = new TH1D(("hc1pull" + iLabel).c_str(), hc1XLabel.c_str(), 20, -5.0, 5.0);
      // asymptotically correct approach
      hntotpull[i] = new TH1D(("hntotpull" + iLabel).c_str(), hntotXLabel.c_str(), 20, -5.0, 5.0);
   }
 
   // number of pseudoexperiments (toys) and number of events per pseudoexperiment
   constexpr std::size_t ntoys = 500;
   constexpr std::size_t nstats = 500;
   // parameters used in the generation
   constexpr double c0gen = 0.0;
   constexpr double c1gen = 0.0;
 
   // Silence fitting and minimisation messages
   auto &msgSv = RooMsgService::instance();
   msgSv.getStream(1).removeTopic(RooFit::Minimization);
   msgSv.getStream(1).removeTopic(RooFit::Fitting);
 
   std::cout << "Running " << ntoys * 3 << " toy fits ..." << std::endl;
 
   // M a i n   l o o p :   r u n   p s e u d o e x p e r i m e n t s
   //----------------------------------------------------------------
   for (std::size_t i = 0; i < ntoys; i++) {
      // S e t u p   p a r a m e t e r s   a n d   P D F
      //-----------------------------------------------
      // angle theta and the weight to account for the acceptance effect
      RooRealVar costheta("costheta", "costheta", -1.0, 1.0);
      RooRealVar weight("weight", "weight", 0.0, 1000.0);
 
      // initialise parameters to fit
      RooRealVar c0("c0", "0th-order coefficient", c0gen, -1.0, 1.0);
      RooRealVar c1("c1", "1st-order coefficient", c1gen, -1.0, 1.0);
      c0.setError(0.01);
      c1.setError(0.01);
      // create simple second-order polynomial as probability density function
      RooPolynomial pol("pol", "pol", costheta, {c0, c1}, 1);
 
      double ngen = nstats;
      if (acceptancemodel == 1)
         ngen *= 2.0 / (23.0 / 15.0);
      else
         ngen *= 2.0 / (16.0 / 15.0);
      RooRealVar ntot("ntot", "ntot", ngen, 0.0, 2.0 * ngen);
      RooExtendPdf extended("extended", "extended pdf", pol, ntot);
      int npoisson = rnd->Poisson(nstats);
 
      // G e n e r a t e   d a t a   s e t   f o r   p s e u d o e x p e r i m e n t   i
      //-------------------------------------------------------------------------------
      RooDataSet data("data", "data", {costheta, weight}, WeightVar("weight"));
      // generate nstats events
      for (std::size_t j = 0; j < npoisson; j++) {
         bool finished = false;
         // use simple accept/reject for generation
         while (!finished) {
            costheta = 2.0 * rnd->Rndm() - 1.0;
            // efficiency for the specific value of cos(theta)
            double eff = 1.0;
            if (acceptancemodel == 1)
               eff = 1.0 - 0.7 * costheta.getVal() * costheta.getVal();
            else
               eff = 0.3 + 0.7 * costheta.getVal() * costheta.getVal();
            // use 1/eff as weight to account for acceptance
            weight = 1.0 / eff;
            // accept/reject
            if (10.0 * rnd->Rndm() < eff * pol.getVal())
               finished = true;
         }
         haccepted->Fill(costheta.getVal());
         hweighted->Fill(costheta.getVal(), weight.getVal());
         data.add({costheta, weight}, weight.getVal());
      }
 
      auto fillPulls = [&](std::size_t i) {
         hc0pull[i]->Fill((c0.getVal() - c0gen) / c0.getError());
         hc1pull[i]->Fill((c1.getVal() - c1gen) / c1.getError());
         hntotpull[i]->Fill((ntot.getVal() - ngen) / ntot.getError());
      };
 
      // F i t   t o y   u s i n g   t h e   t h r e e   d i f f e r e n t   a p p r o a c h e s   t o   u n c e r t a i
      // n t y   d e t e r m i n a t i o n
      //-------------------------------------------------------------------------------------------------------------------------------------------------
      // this uses the inverse weighted Hessian matrix
      extended.fitTo(data, SumW2Error(false), PrintLevel(-1));
      fillPulls(0);
 
      // this uses the correction with the Hesse matrix with squared weights
      extended.fitTo(data, SumW2Error(true), PrintLevel(-1));
      fillPulls(1);
 
      // this uses the asymptotically correct approach
      extended.fitTo(data, AsymptoticError(true), PrintLevel(-1));
      fillPulls(2);
   }
 
   std::cout << "... done." << std::endl;
 
   // P l o t   o u t p u t   d i s t r i b u t i o n s
   //--------------------------------------------------
 
   // plot accepted (weighted) events
   gStyle->SetOptStat(0);
   gStyle->SetOptFit(0);
   TCanvas *cevents = new TCanvas("cevents", "cevents", 800, 600);
   cevents->cd(1);
   hweighted->SetMinimum(0.0);
   hweighted->SetLineColor(2);
   hweighted->Draw("hist");
   haccepted->Draw("same hist");
   TLegend *leg = new TLegend(0.6, 0.8, 0.9, 0.9);
   leg->AddEntry(haccepted, "Accepted");
   leg->AddEntry(hweighted, "Weighted");
   leg->Draw();
   cevents->Update();
 
   // plot pull distributions
   TCanvas *cpull = new TCanvas("cpull", "cpull", 1200, 800);
   cpull->Divide(3, 3);
 
   std::vector<TH1 *> pullHistos{hc0pull[0], hc0pull[1],   hc0pull[2],   hc1pull[0],  hc1pull[1],
                                 hc1pull[2], hntotpull[0], hntotpull[1], hntotpull[2]};
 
   gStyle->SetOptStat(1100);
   gStyle->SetOptFit(11);
 
   for (std::size_t i = 0; i < pullHistos.size(); ++i) {
      cpull->cd(i + 1);
      pullHistos[i]->Fit("gaus");
      pullHistos[i]->Draw("ep");
   }
 
   cpull->Update();
}

 
Running 1500 toy fits ...
... done.
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      12.2745
NDf                       =           12
Edm                       =  3.84566e-06
NCalls                    =           53
Constant                  =      82.0512   +/-   4.52865     
Mean                      =    -0.042844   +/-   0.0572716   
Sigma                     =      1.19191   +/-   0.0392558      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      8.83881
NDf                       =            9
Edm                       =  6.19877e-08
NCalls                    =           53
Constant                  =      104.798   +/-   5.86613     
Mean                      =   -0.0132039   +/-   0.0432773   
Sigma                     =     0.938314   +/-   0.0320986      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      7.28099
NDf                       =           10
Edm                       =  6.30801e-07
NCalls                    =           53
Constant                  =      103.063   +/-   5.55774     
Mean                      =   -0.0233563   +/-   0.0435444   
Sigma                     =     0.954358   +/-   0.0285394      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      23.1247
NDf                       =           14
Edm                       =  2.27317e-06
NCalls                    =           53
Constant                  =      69.5383   +/-   3.95119     
Mean                      =    -0.160071   +/-   0.0652133   
Sigma                     =      1.37036   +/-   0.0473756      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      7.18474
NDf                       =           15
Edm                       =  9.01145e-06
NCalls                    =           61
Constant                  =      51.3838   +/-   3.49309     
Mean                      =    -0.985792   +/-   0.0760226   
Sigma                     =      1.36366   +/-   0.0605719      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      11.9456
NDf                       =           11
Edm                       =  4.88765e-08
NCalls                    =           61
Constant                  =      94.7614   +/-   5.45747     
Mean                      =   -0.0978895   +/-   0.0483575   
Sigma                     =      1.03309   +/-   0.0382346      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      20.9563
NDf                       =           16
Edm                       =  8.77656e-06
NCalls                    =           53
Constant                  =      69.8331   +/-   3.99247     
Mean                      =   -0.0767062   +/-   0.0640105   
Sigma                     =      1.36919   +/-   0.0474577      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      8.84994
NDf                       =           10
Edm                       =  1.85865e-06
NCalls                    =           53
Constant                  =      101.665   +/-   5.77203     
Mean                      =   -0.0558063   +/-   0.0444665   
Sigma                     =      0.96468   +/-   0.0336688      (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      9.73174
NDf                       =           10
Edm                       =  1.95484e-06
NCalls                    =           53
Constant                  =      99.7164   +/-   5.69932     
Mean                      =   -0.0653755   +/-   0.0459247   
Sigma                     =     0.982023   +/-   0.0349408      (limited)

Date

November 2019

Author

Christoph Langenbruch

Definition in file rf611_weightedfits.C.